[ICLR 2020]Network Deconvolution

이번 리뷰는 ICLR 2020-The Best Deep Learning Paper로 선정된 논문에 대해 소개를 하고자 합니다. 또한 fundamental Theory이기에 다른 연구원들에게 도움이 될 거라는 생각에 리뷰를 하고자 결정 했습니다.

Intro

해당 논문에 간략하게 소개하자면, 기존 CNN은 convolution을 이용합니다. convolution은 데이터간 correlation을 더 강하게 만드는 방향으로 크기가 줄어든(중복성을 가진) feature를 추론합니다. 하지만 이는 NN의 학습을 어렵게 만든다고 주장합니다.
이를 해결하기위해서 Network Deconvolution을 제안했습니다. 이는 데이터가 각 계층에 공급되기 전에 픽셀 단위 및 채널 단위의 correlation을 최적으로 제거하는 절차를 수행합니다.
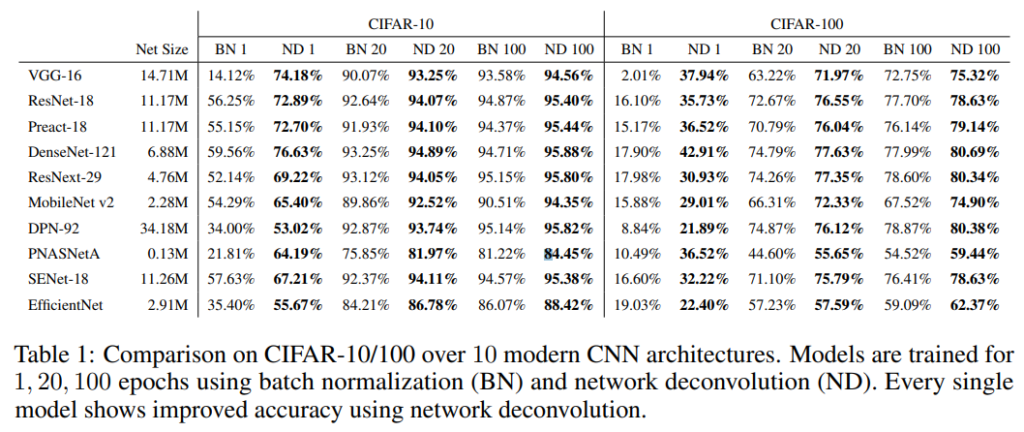
Network Deconvolution의 효과를 증명하기 위해서 CIFAR-10, CIFAR-100, MNIST, Fashion-MNIST, Cityscapes, ImageNet datasets에서 VGG, ResNet, DenseNet, ResNext, MobileNet, SENet, EfficientNet의 성능을 평가 했으며, 성능 향상을 증명했습니다(Table 1 참고, 이하 다른 Dataset에서의 성능 지표는 Experiment 참고).
++ torch로 짜여진 Deconvolution 코드를 논문에 첨부했습니다.

Deep Learning 분야에서 많이 사용되고 우리가 알던 Deconvolution(fig 1)은 feature를 up-sampling하기 위한 용도로 사용됩니다. feature map의 크기를 변경하는 용도이기에 transpose convolution이라는 명칭이 보다 개념을 잘 표현하는 의미이며, Deconvolution보다 앞서서 나온 명칭이라고 합니다.

그럼 Deconvolution은 무엇일까요? 이번에 리뷰한 논문에서는 수학적인 의미에서의 Deconvolution을 제안을 합니다. 즉, x * conv = y 라면, y * inv(conv) = x일 때, inv(conv) 필터가 진정한 의미에서 Deconvolution라고 볼 수 있습니다.

MOTIVATIONS

먼저 해당 논문의 모티브는 선형 회귀 문제를 pseudo inverse(closed form solution)로 푼다면, 한번의 iteration으로 풀 수 있다는 점에서 시작합니다.

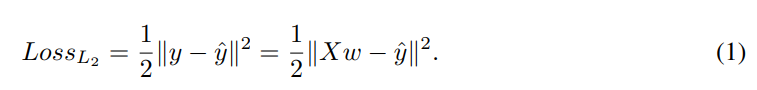
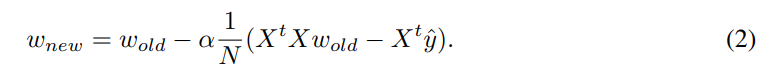
수식 1은 L2 loss이며, 선형 회귀에서는 수식 2와 같은 방법으로 gradient descent를 진행합니다.

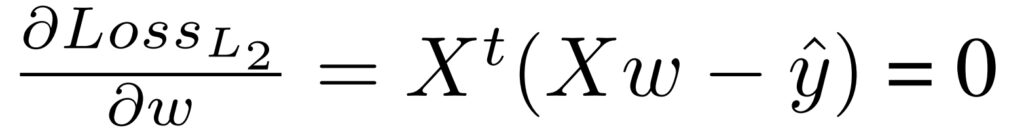
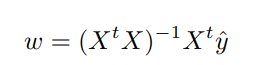
L2 loss를 최소화하는 방향을 학습하기 위해 미분을 한다면 수식 3의 모습을 가집니다. 또한 수식 3이 0이라면 해당 값은 최적화된 값에 수렴했다고 볼 수 있습니다. 수식 3의 weight를 얻기 위해 x의 pseudo inverse를 만들어 정리한다면, 수식 4의 모습이 나옵니다. 즉 1/N * X^t X = I(Hessian Matrix)를 구할 수 있다면 선형 회귀 한정 한번의 iteration으로도 최적화된 값을 얻을 수 있습니다. 그렇기에 data의 correlation 문제로 귀결된다고 볼 수 있으며, correlation이 최소화될 경우에 학습에 긍정적인 효과를 미친다는 것을 알 수 있습니다.(Hessian matrix = I가 될려면 correlation이 0이여야 함,)

그럼 convolution에서는 어떻게 적용할 수 있을 까요?
데이터의 pseudo inverse를 구하기 용이하도록 먼저 영상 데이터를 column vector화를 진행합니다.

fig 3-왼쪽 처럼 각 conv의 kernel이 곱해지는 영역을 vectorize하여 column vector화 한 후, concat 해줍니다. 여러 채널을 가지고 있는 경우 horizontal 방향으로 concat 해줌으로써 X를 구합니다.

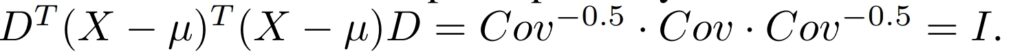
fig 3-오른쪽 상단 처럼 Covariance matrix Cov = 1/N X^t X를 구합니다

수식 5를 구할 수 있으며, 이는 1/N * X^t X = I과 유사하다고 볼 수 있다고 합니다. 그렇기에 수식 3에 수식 5 방벙을 적용한다면 x * D *w = y, 로 바로 수렴이 가능하다고 볼 수 있습니다.

++ 저자는 아래의 글에서 k_cov를 역인 커널을 사용하기에 deconvolution이라고 칭해도 괜찮다고 합니다.

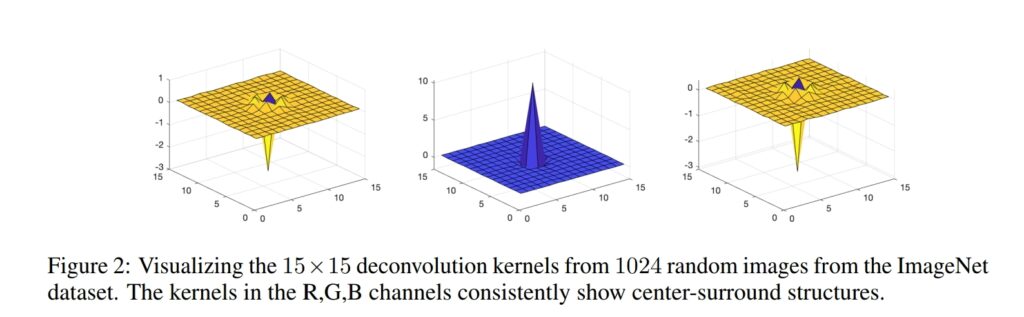
추가로 저자는 deconvolution kernel을 시각화한 모습(Fig 2)이 실제 동물의 시각 중추에서 보여주는 형태와 유사하기 때문에 생물학적인 부분에서도 효과를 증명할 수 있다고 합니다.

Experiment

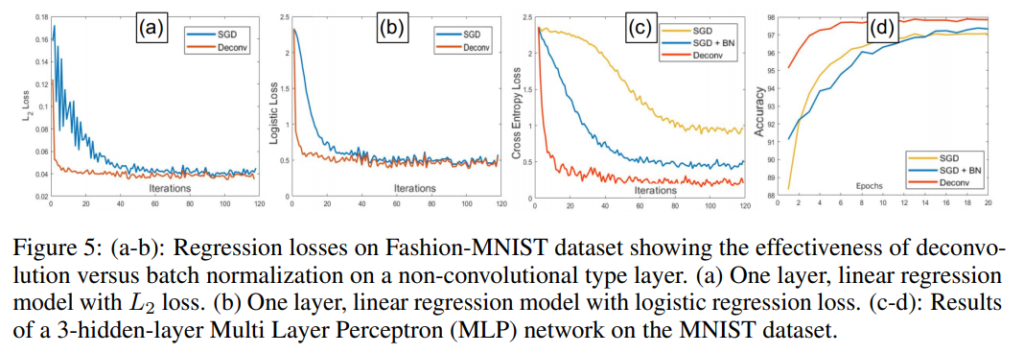
SGD와 BN을 사용 했을 때보다 빠른 속도로 수렴하는 모습을 확인 할 수 있습니다. 이를 통해 correlation 줄이는 것이 학습 속도 향상에 효과적인 걸 알 수 있습니다.

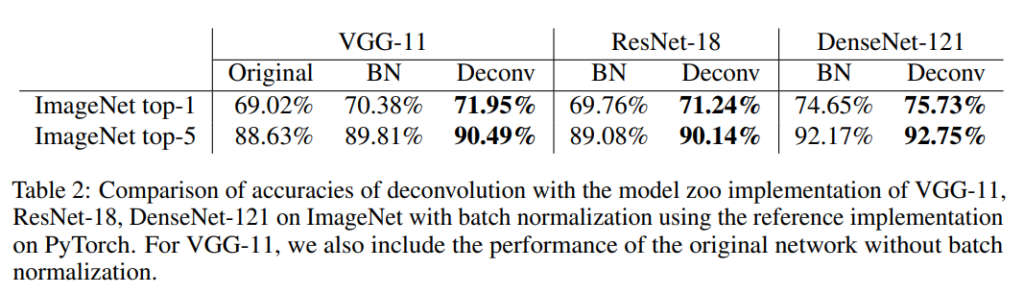
table 1~2를 통해 BN을 사용한 방방법다 개선된 성능을 얻을 걸 볼 수 있습니다.

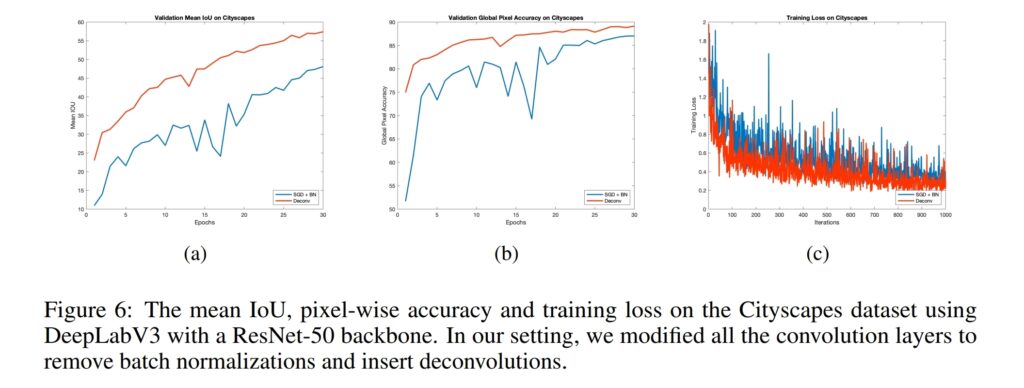
또한 Segmentation task에서도 성능 향상을 가져온 걸 확인 할 수 있습니다.