이번에 소개드릴 논문은 FlashAttention이라는 논문입니다. 사실 FlashAttention은 예전부터 경량화 관련된 논문을 읽으면 자주 등장했던 용어로 제가 관심을 가지고 있었는데 계속 미루고 미루다가 이번에 한번 읽어보게되었습니다. 벌써 FlashAttention이 V3까지 나온걸로 아는데 일단 이번에 소개드릴 논문은 가장 처음으로 나온 FlashAttention-V1에 대한 논문입니다.
Intro
Transformer 모델은 자연어 처리(NLP)와 이미지 분류 등 다양한 분야에서 표준 아키텍처로 자리 잡았습니다. 모델의 크기와 깊이는 계속 커지고 있지만, 정작 입력할 수 있는 문맥의 길이(Context length)를 늘리는 데에는 한계가 있었습니다. 가장 큰 원인은 Transformer의 핵심인 Self-Attention 모듈의 시간 및 메모리 복잡도가 시퀀스 길이($N$)의 제곱($O(N^2)$)에 비례하여 증가하기 때문입니다.
이러한 계산 복잡도를 해결하기 위해, 그동안 많은 ‘근사(Approximate) Attention’ 방법론들이 제안되었습니다. 이들은 연산량(FLOPs)을 줄이기 위해 행렬을 희소(Sparse)하게 만들거나 저랭크(Low-rank)로 근사하는 방식을 택했습니다. 하지만 이러한 방법들은 이론적인 연산량을 줄였음에도 불구하고, 실제 학습 속도(Wall-clock speedup)는 크게 개선되지 않는 경우가 많았습니다. 저자들은 그 이유를 메모리 접근 비용(IO overhead)에서 찾습니다. 기존 연구들은 연산 횟수를 줄이는 데만 집중했을 뿐, GPU 메모리 계층 간의 데이터 이동 시간은 간과했기 때문입니다.
본 논문은 Attention 알고리즘 설계 시 ‘IO-Awareness’가 필수적이라고 주장합니다. 최신 GPU는 연산 속도에 비해 메모리 대역폭(Bandwidth)이 현저히 느립니다. 따라서 전체 수행 시간은 연산 시간이 아닌, 데이터를 메모리에서 읽고 쓰는 시간(Memory Access)에 의해 결정됩니다. 특히 GPU 메모리는 용량이 크지만 느린 HBM(High Bandwidth Memory)과 용량은 작지만 매우 빠른 SRAM(On-chip Memory)으로 나뉩니다.
FlashAttention은 이러한 하드웨어 특성을 고려하여, 느린 HBM에 대한 접근 횟수를 최소화하는 Exact Attention 알고리즘입니다. 이를 위해 Tiling(타일링) 기법을 사용하여 큰 행렬을 작은 블록 단위로 쪼개어 빠른 SRAM 위에서 연산을 수행합니다. 또한, 역전파(Backward pass) 과정에서 거대 Attention 행렬을 저장하지 않고 **재연산(Recomputation)**하는 방식을 통해 메모리 사용량을 시퀀스 길이에 대해 선형($O(N)$)으로 줄였습니다. 결과적으로 FlashAttention은 기존의 표준 Attention보다 빠른 속도를 보이면서도 근사(Approximation) 없는 정확한 결과를 산출하며, 더 긴 Context를 효율적으로 학습할 수 있게 합니다.
Background
이 논문을 이해하기 위해서는 먼저 GPU의 메모리 계층 구조(Memory Hierarchy)를 알아야 합니다. GPU 메모리는 크게 두 가지로 나뉩니다.
- HBM (High Bandwidth Memory): 우리가 흔히 ‘VRAM’이라 부르는 메인 메모리로 용량은 크지만(40~80GB), 속도는 상대적으로 느림.
- SRAM (On-chip Memory): GPU 연산 유닛 바로 옆에 붙어 있는 캐시 메모리로 속도는 HBM보다 훨씬 빠르지만(약 10배 이상), 용량이 매우 작음(약 20MB 수준).
저자들은 최근 GPU의 연산 속도(Compute)는 비약적으로 발전했지만, 메모리 대역폭(Memory Bandwidth)의 발전은 그에 미치지 못했다는 점을 지적합니다. 이로 인해 현대 딥러닝 연산의 병목은 ‘얼마나 빨리 계산하느냐(Compute-bound)’가 아니라, ‘얼마나 빨리 데이터를 퍼 나르느냐(Memory-bound)’에 달려 있는 경우가 많습니다.
표준 Attention 알고리즘(S=QK^T, P=\text{softmax}(S), O=PV)은 대표적인 Memory-bound 연산입니다. 그 이유는 중간 결과물인 Attention Matrix (S, P) 때문입니다. 표준 구현체는 다음과 같은 순서로 작동하며, 단계마다 거대한 N \times N 크기의 행렬을 HBM에 쓰고 읽기를 반복합니다.
- Q와 K를 HBM에서 읽어와 S=QK^T를 계산하고, 그 거대한 결과(N^2)를 다시 HBM에 기록합니다.
- HBM에서 S를 다시 읽어와 Softmax를 취해 P를 만들고, 이를 또 HBM에 기록합니다.
- HBM에서 P와 V를 읽어와 최종 결과 O를 계산합니다.
문제는 시퀀스 길이(N)가 길어질수록 이 중간 행렬(S, P)의 크기가 제곱(N^2)으로 커진다는 점입니다. 단순히 메모리 용량을 많이 차지하는 것을 넘어, 이 거대한 데이터를 느린 HBM에 쓰고 읽는 과정 자체가 심각한 시간 지연을 초래합니다. 기존 연구들이 연산 횟수(FLOPs)를 줄이는 데 집중했다면, FlashAttention은 **”중간 행렬을 굳이 HBM에 갔다 놓을 필요가 있는가?”**라는 근본적인 의문을 제기합니다.
An Efficient Attention Algorithm With Tiling and Recomputation
FlashAttention의 목표는 정확한(Exact) Attention 값을 계산하면서도, 느린 HBM(High Bandwidth Memory) 접근을 획기적으로 줄이는 것입니다. 이를 위해 저자들은 타일링(Tiling)과 재연산(Recomputation)이라는 두 가지 핵심 기법을 제안합니다.
Attention 연산의 가장 큰 난관은 Softmax 함수입니다. Softmax는 행렬의 한 행(Row) 전체에 대한 합계(분모)를 알아야 각 원소의 확률값을 구할 수 있기 때문에, 행렬을 블록 단위로 쪼개서 독립적으로 계산하는 것이 불가능해 보입니다(Coupling issue).
저자들은 이를 해결하기 위해 Softmax 분해(Decomposition) 기법을 활용합니다. 벡터 x를 두 개의 블록 x^{(1)}, x^{(2)}로 쪼개더라도, 각 블록의 ‘로컬 최대값(m)’과 ‘지수 합(l)’ 정보만 유지하면 전체 Softmax 결과를 수학적으로 완벽하게 복원할 수 있다는 점에 착안했습니다.
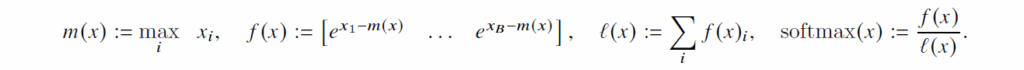
Recomputation
딥러닝의 학습(Backward Pass)을 위해서는 순전파(Forward Pass) 때 계산했던 N \times N 크기의 Attention 행렬(S, P)이 필요합니다. 기존 방식은 이를 HBM에 저장해 두었는데, 이는 엄청난 메모리 공간을 차지할 뿐만 아니라 저장하고 다시 불러오는 시간(IO)이 매우 오래 걸렸습니다. 그래서 저자들은 한가지 재밌는 방식으로 이를 해결하는데 바로 “저장하지 말고, 필요할 때 다시 계산하자”는 것입니다.
- 저장 최소화: 순전파 단계에서 거대한 행렬 S, P를 저장하는 대신, 앞서 구한 가벼운 통계치 벡터 m, l (크기 O(N))과 출력값 O만을 HBM에 저장합니다.
- 재연산 수행: 역전파 단계에서 S, P가 필요해지면, 저장해 둔 Q, K, V 블록을 SRAM으로 가져와서 SRAM 위에서 빠르게 다시 계산합니다.
- 속도 향상: 언뜻 보면 연산량(FLOPs)이 늘어나 느려질 것 같지만, GPU에서는 HBM 접근 속도가 연산 속도보다 훨씬 느리기 때문에(Memory-bound), HBM 입출력을 줄이고 연산을 더 수행하는 것이 전체 수행 시간(Wall-clock time)을 단축시킵니다.
이 모든 과정(입력 로드 -> 행렬 곱 -> Softmax -> Masking/Dropout -> 행렬 곱 -> 출력 저장)은 하나의 CUDA 커널 안에서 융합(Fusion)되어 수행됩니다. 이를 통해 중간 데이터를 HBM에 썼다가 다시 읽는 오버헤드를 원천적으로 차단했습니다.
위의 과정들을 토대로 실제 FlashAttention이 어떻게 동작하는지에 대해 과정을 나타낸 것이 바로 아래 알고리즘1입니다.
우선 첫번째 라인은 빠른 메모리인 SRAM의 크기(M)에 맞춰서 행렬을 자를 블록 크기( B_c, B_r)를 결정합니다. 이후 2번째 라인에서 Recomputation(재연산)을 위한 준비를 하는데, 거대한 N \times N 행렬(S, P)을 저장할 공간을 만들지 않고, 대신 가벼운 통계치 벡터 l (지수 합), m (최대값)과 결과값 O만 초기화합니다.
이후 Attentnion 연산의 입력으로 들어온 데이터 Q, K, V 행렬을 실제로 블록 단위(T_r, T_c 개)로 나눕니다. line6은 IO-Awareness (메모리 효율화)입니다. K와 V의 한 블록을 느린 HBM에서 빠른 SRAM으로 가져옵니다. 이 블록은 내부 루프가 도는 동안 SRAM에 계속 머물며 재사용되므로 HBM 접근을 최소화합니다.
line8은 현재 계산할 Q 블록과, 지금까지 누적된 결과([laex]O_i[/latex]) 및 통계치(l_i, m_i)를 SRAM으로 불러옵니다. 이후 line9에서 Tiling 연산을 수행하는데 SRAM 위에서 작은 블록 단위의 행렬 곱을 수행하는 것을 의미합니다.
Line 10~12가 상당히 중요한 부분으로, 아까 위에서 소개드린 Softmax Decomposition에 대한 내용입니다. 우선 Line10에서 현재 블록(S_{ij}) 내부에서의 ‘로컬’ 최대값(\tilde{m})과 지수 합(\tilde{l})을 계산합니다.
이후 Line11에서 통계치 update를 진행하게 됩니다. 지금까지 알고 있던 전역 최대값(m_i)과 현재 블록의 로컬 최대값(\tilde{m}_{ij})을 비교해 새로운 최대값(m_i^{new})을 찾고, 지수 합도 이에 맞춰 갱신합니다.
이후 Line12에서는 Line11에서 최대값이 바뀌었으므로, 기존에 계산해둔 결과값(O_i)에 보정 계수(e^{m_i - m_i^{new}})를 곱해주고, 현재 블록의 결과를 더해줍니다. 이렇게 하면 전체 행렬을 다 보지 않고도 정확한 Softmax 결과를 누적해 나갈 수 있습니다.
마지막으로 Line13에서 다음 스텝(또는 Backward Pass)을 위해 갱신된 통계치를 HBM에 저장합니다. 여기서 S_{ij}, P_{ij} 같은 거대 행렬은 HBM에 저장하지 않고 버립니다. 이것이 바로 Recomputation 전략의 핵심으로, 메모리를 아끼는 대신 나중에 역전파 때 SRAM 위에서 다시 계산하게 됩니다.
Analysis: IO Complexity of FlashAttention
지금까지 FlashAttention의 동작 과정에 대해서 살펴보았으니, 그럼 과연 FlashAttention이 실제로 빠르고 효율적인가?에 대해 알아보겠습니다.
저자들은 알고리즘의 효율성을 비교하기 위해 연산 횟수(FLOPs)가 아닌 HBM 접근 횟수(IO Complexity)를 척도로 사용합니다. 이는 앞서 언급했듯, 최신 GPU 환경에서는 메모리 접근이 주된 병목이기 때문입니다. 분석에서 N은 시퀀스 길이, d는 헤드 차원, M은 SRAM의 크기를 의미합니다.
표준 Attention의 한계: O(N^2) 표준 Attention 구현은 연산 단계마다 거대한 중간 행렬(N \times N 크기의 S, P)을 HBM에 쓰고 읽어야 합니다.
- S = QK^T 계산: S를 HBM에 씀 (N^2 접근).
- P = \text{softmax}(S) 계산: S를 읽고 P를 (2N^2 접근).
- O = PV 계산: P를 읽고 O를 씀 (N^2 접근).
결과적으로 총 메모리 접근 횟수는 시퀀스 길이의 제곱인 \Theta(N^2)에 비례합니다. N이 커질수록 이 비용은 감당할 수 없이 늘어납니다.
반면 FlashAttention 경우 알고리즘1에서도 보셨다시피 타일링을 통해 이 비용을 획기적으로 낮췄습니다. 입력 행렬 K, V를 SRAM 크기(M)에 맞는 블록 단위로 로드합니다. 외부 루프가 한 번 돌 때마다 K, V 블록은 SRAM에 고정(Reuse)되고, 그동안 Q의 모든 블록을 순회하며 연산을 수행하는 것이죠.
이러한 연산 방식을 통해 FlashAttention의 총 HBM 접근 횟수는 \Theta(N^2 d^2 M^{-1})를 가지게 됩니다. 이는 표준 방식(N^2)과 비교했을 때, 분모에 SRAM 크기 M이 들어갑니다. 보통 M(SRAM 크기)은 d^2(헤드 차원의 제곱)보다 훨씬 크기 때문에, FlashAttention은 표준 방식보다 M/d^2배만큼 메모리 접근을 덜 하게 됩니다. 실제로 이는 수배에서 수십 배에 달하는 접근 횟수 감소를 의미합니다. 기존 attention 연산과 flash attention 연산 사이의 결과를 정리하면 아래 그림과 같습니다.
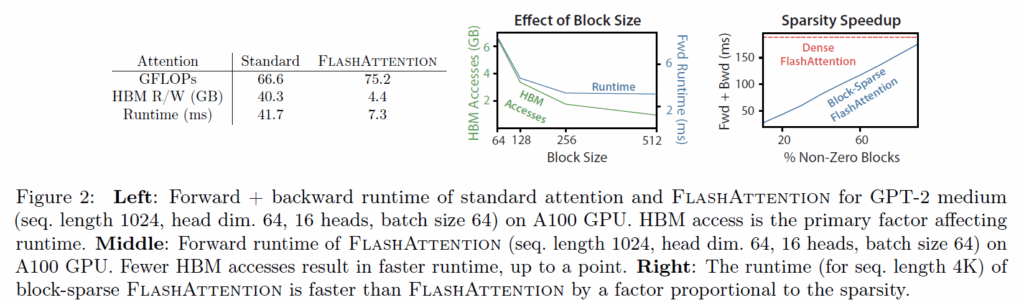
좌측표 보시면 FlashAttention이 기존 Attention 방식 대비 재연산(Recomputation)으로 인해 FLOPs는 약간 늘어났지만, 전체 실행 시간을 지배하는 HBM 접근 횟수가 획기적으로 줄어들었기 때문에 실제 Wall-clock time은 훨씬 빨라집니다. 그래프(Fig 2)는 블록 크기(B_c)를 키울수록 HBM 접근이 줄어들어 속도가 빨라지는 경향을 통해 이론과 실제가 일치함을 보여줍니다.
Experiments
저자들은 FlashAttention이 단순히 이론적으로만 빠른 것이 아니라, 실제 모델 학습에서도 속도와 성능 향상을 가져온다는 것을 입증하기 위해 광범위한 실험을 수행했습니다. 실험은 크게 세 가지 파트로 나뉩니다.
- 학습 속도 검증 (Faster Models) 기존의 표준 Attention 구현체들과 비교하여 실제 모델을 학습시키는 데 걸리는 시간(Wall-clock time)을 측정했습니다.
- 긴 시퀀스 모델링 성능 (Better Models with Longer Sequences) FlashAttention의 메모리 효율성을 활용하여 Context Length를 늘렸을 때, 모델의 성능이 얼마나 향상되는지 평가했습니다.
- 벤치마킹 (Benchmarking Attention) 다양한 시퀀스 길이(128 ~ 64K)에 따른 런타임과 메모리 사용량을 정밀 측정했습니다.
학습 속도 검증에서는 BERT와 GPT2모델을 각각 Wikipedia 데이터셋과 OpenWeb Text dataset로 학습하였으며, 표준 attention 사용 모델 대비 FlashAttention 사용 모델의 학습 시간이 얼마나 효율적으로 개선되었는지를 평가하였습니다.
우선 BERT 모델에 대한 결과입니다. 결론부터 말씀드리면 기존 구현 대비 FLASHAttention을 적용하였을 때 평균 학습 시간이 2.5분 더 개선된 것을 확인할 수 있습니다. 고작 2.5분?이라고 생각하실 수 있지만 퍼센테이지로 따지면 학습 속도를 13% 개선한 것으로 생각하시면 됩니다.
다음은 GPT에 대한 결과입니다.
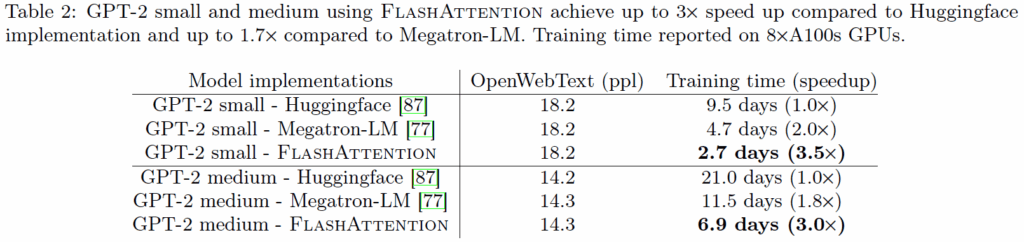
ppl은 언어모델의 성능 지표인 PerPlexity라는 의미로, 기존 huggingface와 Megatron-LM의 구현대비 FlashAttention이 동일한 성능에 도달하기까지 학습 시간은 9.5days vs 4.7days vs 2.7days로 무려 hugging face 대비 3.5배 더 빠른 것을 살펴보실 수 있습니다. GPT-2 medium에 대해서도 마찬가지로 3배 더 빠른 모습을 보여주고 있구요.
다음은 긴 시퀀스 처리가 필요한 다양한 태스크(텍스트, 이미지 등)에서의 성능을 종합적으로 평가합니다.
비교가 되는 방법론들로는 표준 Transformer 및 Linformer, Performer, Reformer 등 다양한 Approximate Attention(근사 어텐션) 모델들로 구성이되어 있는 모습입니다. Block-sparse FlashAttention은 FlashAttention을 근사 어텐션 방식으로 구현한 것을 의미하며, 이는 훨씬 킨 시퀀스를 처리하는데 있어 장점이 있다 합니다.
결론을 말씀드리면, FlashAttention은 표준 Transformer 대비 2.4배, Block-Sparse 버전은 2.8배 빠르며 이는 기존의 근사 attention 방식들과 비교해도 가장 빠른 속도를 보여주고 AVG 성능도 가장 높은 것을 확인하실 수 있습니다.
이렇게 저자들이 제안하는 FlashAttention은 빠르고 효율적인 attention이 가능하여 속도가 빨라진 덕분에 더 긴 문맥을 넣을 수 있게 되었으며, 저자들은 이를 증명하고자 아래와 같이 Context Length를 늘리는 실험을 진행합니다.
기존 Baseline이 1K Context Length를 지니면서 학습 시간은 4.7일이 걸리고 이때의 ppl 값은 18.2이였습니다. 하지만 저자들의 FlashAttention을 적용하여 Context Length를 무려 4배인 4K로 늘렸을 경우 학습 시간은 여전히 30%더 빠르지만 더 긴 length를 활용한 덕분에 ppl 값은 17.5로 줄어들어 모델의 성능이 더 좋아짐을 보입니다.
결론
FlashAttention은 기존의 연구들이 GLFOPS를 개선하는 것에만 집중하던 것과 달리, 모델의 학습 및 추론에 매우 중요한 GPU의 물리적 특성을 고려하여 attention 연산을 재설계하는 방식을 통해 매우 인상적인 결과를 나타낸 것으로 보입니다. 이러한 파급력 덕분에 해당 논문이 등장한지 3년 정도 된 것 같은데 벌써 인용수가 3400회가 넘었네요.
