
주로 image 나 video를 이용한 Retrieval task에서는 입력을 임의의 vector로 e hashing (이와 비슷하게 encoding 이라고도 합니다.) 한 후, vector 들 간의 유사도를 계산해 차이가 가장 작은 것을 찾습니다. Retrieval에서 대표적인 방법론, NetVLAD에서는 입력 영상을 KxD의 크기로 hashing 하게 되고 이를 Triplet loss로 학습시킵니다. (K는 cluster의 개수, D는 backbone network에서 나온 출력 값의 차원입니다.) 이처럼 Pairwise하게 학습시키거나 Triplet 방식으로 학습시켜 hashing 하게 될 시 다음과 같은 문제가 생기게 됩니다.
- 전체 학습데이터셋을 가지고 유사도를 학습시킬 때 효율성이 낮습니다. Pairwise와 Triplet 방식은 시간복잡도가 O(n!)으로 알려져 있는데 이는 대용량 데이터셋을 사용할 시 시간적인 효율성이 낮습니다.
- 데이터가 잘 구별되지 않습니다. 두 방식을 사용할 때, 데이터 쌍의 부분적인 관계를 보기 때문에 hashing된 vector의 구별성이 떨어지게 됩니다.
- 분포가 불균형한 데이터셋에서 사용시 효율적이지 못합니다. 실생활에서는 불균형한 데이터가 많은데 두 방식은 이를 잘 구분해내지 못하여 성능을 제한 시킵니다.
본 논문의 저자는 이를 해결하기 위해 좀 더 좋은 hash function을 얻게 해주는 Central similarity 라는 방식을 제안하게 됩니다.
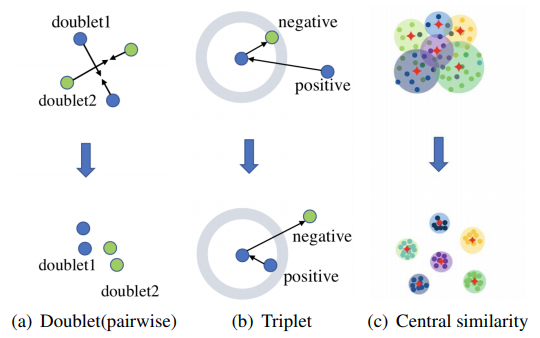
이 방식은 몇개의 대표되는 hash center와 hash function을 통해 hashing된 hash code 사이의 Hamming distance를 측정하고 hash code에 해당되는 hash center와의 Hamming distance를 줄이는 것을 목표로 하게 됩니다. 여기서 Hamming distance란 두 vector 사이에서 다른 부분의 개수를 의미 합니다. 예를 들어, 11010과 11111이라는 vector가 있다면 다른 부분이 두 곳이므로 이 둘 사이의 Hamming distance는 2 입니다. 또한 abcdef와 abcccc 라는 문자열이 있다면 이 둘 사이의 Hamming distance는 3이 됩니다.
그리고 모든 데이터(n)를 hash center(m)에 대해 계산하기 때문에 시간 복잡도 또한 O(nm)이 되게 됩니다. 제안된 이 방식은 널리 알려져 있는 K-Means 알고리즘과는 유사하지만 K-Means 알고리즘은 center를 선정하고 있는 feature를 각 center에 할당하는데에 반해 Central similarity 방식은 할당 후 center와의 거리를 줄이는 차이가 있고, NetVLAD와도 유사하지만 NetVLAD는 center를 학습시키는 반면 Central similarity 방식은 feature를 학습시키는 차이가 있습니다.

1. Method
1.1. Definition of Hash Center
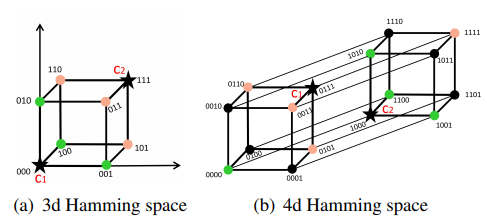
저자는 Hash center를 pre-define 하여 사용하였는데 이를 다음과 같은 조건으로 정의 하였습니다.
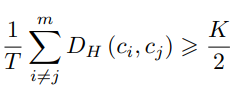
여기서 Hash center는 K차원의 Hamming space에서 C = \{c_{i}\}_{i=1}^{m} \subset \{0,1\}^{K} 와 같이 나타나게 됩니다. D_{H}는 Hamming distance, m은 Hash center의 개수, T는 서로 다른 c_{i}, c_{j}의 조합 수 입니다.
이러한 조건에 맞는 Hash center가 Fig 4에서 c_{i}, c_{j} 와 같이 존재할 때 다른 데이터들과 Hash center와의 거리를 구한 뒤 각 데이터들 기준 가장 가까운 거리로 이루어져 있는 Hash center를 할당하게 됩니다.
추가로 저자가 제안한 pre-defined center는 실험적으로 learned center 방식보다 더 좋은 성능을 내어 효력을 입증하였습니다. 제안된 방식은 hashing 후 binarize 되어 나오지만 learned center 방식은 hashing 후 binarize를 따로 하기에 유사도 정보를 손실시키기 때문이라 합니다.
1.2. Generation of Hash Centers
저자는 식 (1)에 해당하는 Hash center를 생성하기 위해 두가지 방법을 고안해내었습니다. 이 방법들은 K 차원 Hamming space에서 center 집합들이 서로 직교하며 동일한 거리 K/2를 갖게 합니다.
우선 첫번째 방식은 Hadamard matrix의 성질을 활용하여 Hash center를 생성하는 것입니다. Hadamard matrix( H_{K} = [h_{a}^{1};...;h_{a}^{K}])는 정방행렬이며 각 행벡터들끼리와 열벡터들끼리 직교하는 성질을 가지고 있습니다. 이러한 성질로 임의의 두 행을 서로 내적하였을 때 <h_{a}^{i}, h{a}^{j}> = 0 이라는 결과가 나오게 되고, 이를 통해 두 행벡터 사이의 Hamming Distance는 D_{H}(h_{a}^{i}, h_{a}^{j}) = \frac{1}{2}(K-<h_{a}^{i}, h{a}^{j}>) = K/2 가 되므로 행백터들로부터 Hash center를 얻을 수 있게 됩니다. 이때 K는 2의 제곱이며 Hash code의 bit를 의미하게 됩니다. 그리고 Hadamard의 원소는 1과 -1로 이루어지지만 -1을 0으로 대체하게 된다면 \{0,1\}^{K} 의 Hash center를 얻을 수 있게 됩니다. 또한, Hash center의 수 m이 보다 같거나 작으면 Hadamard matrix의 행을 직접적으로 Hash center로 사용하면 되지만 만약 K<m<=2K 라면 두개의 Hadamard matrix을 이어 붙여 Hash center를 사용하게 됩니다.
이와 같은 첫번째 방식은 만약 m이 2K보다 크거나 K가 2의 배수가 아니라면 사용할 수 없게 됩니다. 그래서 저자는 center의 bit를 무작위로 샘플링 하는 두번째 방식도 고안해 내었습니다. 두번째 방식은 center의 각 bit에 Bernoulli distribution 의 확률 변수가 0.5일 때를 기준으로 정해 각각 1과 0을 넣는 방식이며 이와 같은 방법으로 만든 Hash center 끼리의 Hamming distance의 기댓값은 K/2인 것으로 식(1)의 조건을 만족하는 것을 알 수 있습니다.

1.3. Semantic Hash centers for single & multi label data
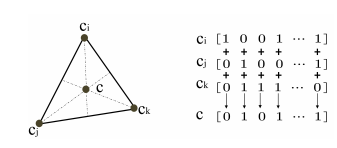
Hash center를 생성한 후 각 데이터를 center에 맞게 label을 붙여 주게 되는데 만약 single-label일 경우 Hash code와 Hash center의 Hamming distance가 가장 작은 center를 할당하면 됩니다. 그러나 multi-label일 경우에는 다른 방법을 사용하게 됩니다. 만약 한 데이터에 label이 c_{i}, c_{j}, c_{k}의 l_{i}, l_{j}, l_{k} 로 할당되었다면 이 center들이 1과 0으로 구성되어 있기에 각 bit마다 voting 을 하여 하나의 center label로 만들어 주게 됩니다. 그리고 만약 1인 개수와 0인 개수가 같다면 Bernoulli distribution 의 확률 변수가 0.5일 때를 기준으로 1과 0을 랜덤하게 선택하게 됩니다.
1.4 Central Similarity Quantization
생성된 Hash center와 데이터를 이용해 학습 시키기 위해 MAP(Maximum a Posterior)라고 불리우는 최대 사후 확률을 이용해 central similarity를 학습시키게 됩니다. 이를 토대로 아래의 식 (2)를 최대화하게 된다면 모든 학습데이터에 대한 Hash code의 MAP 추정을 할 수 있게됩니다.
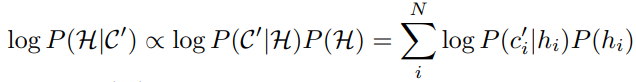
여기서 P(H) 는 Hash code에 대한 사전 분포이고 P(C'|H) 는 likelihood function 입니다. 그리고 P(c'_{i}|h_{i}) 는 Hash code h_{i} 가 그에 할당된 center c'_{i} 일 조건부 확률입니다. 이 조건부 확률만 MAP에서 빼내어 이를 Gibbs distribution으로 모델링 하게 된다면 P(c'_{i}|h_{i}) = \frac{1}{\alpha}exp(-\beta D_{H}(c'_{i}, h_{i})) 로 할 수 있습니다. 식에서 \alpha, \beta 는 상수를 나타내며 D_{H} 는 Hash code와 Hash center 간의 Hamming distance를 나타내게 됩니다. 또한, Hash center는 binary vector 이므로 Hamming distance를 구하기 위해 BCE(Binary Cross Entropy)를 사용할 수 있습니다. 이를 통해 조건부확률 P(c'_{i}|h_{i}) 는 \frac{1}{K}\Sigma_{k \in K}((c'_{i,k})log(h_{i,k}) + (1-c'_{i,k})log(1-h_{i,k})) 로 계산될 수 있으며 조건부확률이 커질수록 Hash code와 Hash center의 Hamming distance가 작아지는 것을 알 수 있습니다. 이러한 이유로 저자는 MAP의 조건부 확률에서 모델링한 식 (3)을 central similarity loss L_{c} 로 사용하였습니다.
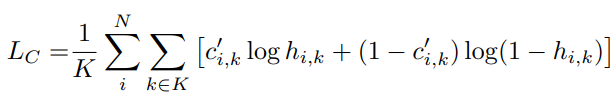
그러나 이렇게 정의된 central similarity loss는 Hash center가 binary이기에 최적화 하는데 어려움이 있어 각 Hash code가 Hash center로 수렴하는 것을 보장할 수 없게 됩니다. 이러한 이유로 인해 저자는 Hash code의 수렴을 돕는 quantization loss L_{Q} 도 추가하였습니다. L_{Q} 는 DHN(Deep hashing network for efficient similarity retrieval)에서 사용한 방식과 유사하게 bi-modal Laplacian prior for quantization을 사용하였으며 미분 계산의 편의를 위해 log cosh 함수가 |x| 유사함을 토대로 이를 도입해 식 (4)를 quantization loss로 설계하였습니다.
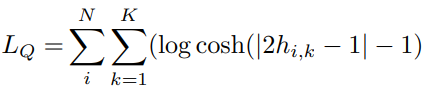
식 (3)과 식 (4)를 합쳐 최종적인 Loss 함수 L_{T} 식 (5)를 설계하였으며 여기서 \theta 는 deep hash function learning에 사용되는 모든 파라미터이고 \lambda_{1} 은 저자가 grid search를 통해 얻어낸 하이퍼 파라미터 입니다.
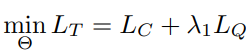
결과적으로 feature를 추출하는 backbone layer와 (3개의 fc layer, ReLU)로 구성된 hash layer, 그리고 Loss 함수 L_{T} 로 deep-hashing 방식인 CSQ 가 구성되게 됩니다.
2. Experiments
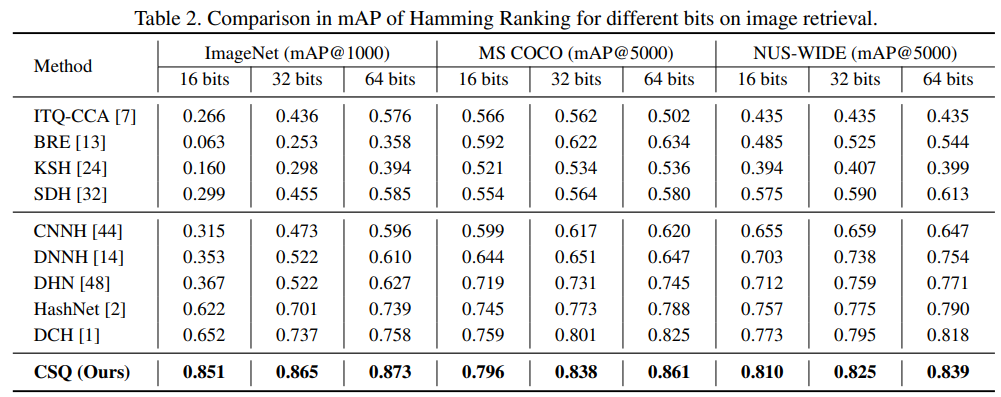
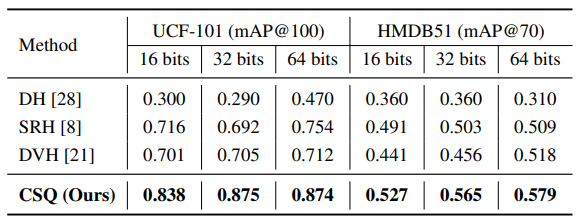
Table 1과 Table 2를 통해 제안된 방법이 image와 video retrieval에서 SOTA의 성능을 보인 것을 확인할 수 있습니다.
3. Reference
[1] https://arxiv.org/pdf/1908.00347.pdf
[2] https://en.wikipedia.org/wiki/Hadamard_matrix