이번에 리뷰로 작성할 논문은 CVPR2025에 게재된 GeoDepth라는 논문이며, 해당 논문은 self-supervised monocular depth estimation task를 다루고 있습니다.
Intro
지난번 리뷰에서도 마찬가지로 self-supervised monocular depth estimation(SDE)는 이미지만으로 깊이 추정을 학습시킬 수 있다는 점에서 예전에 많은 관심을 받은 분야였습니다. 다만 이 SDE는 target frame과 해당 프레임의 앞 또는 뒤의 source frame들 사이의 카메라 포즈를 계산하고 타겟 프레임의 Depth와 해당 포즈를 통해 소스프레임을 타겟프레임으로 warping해서 학습을 하는 과정을 수행하게 됩니다.
이러한 warping을 통한 학습 방식은 정적인 영역에 대해서만 올바르게 동작하기 때문에 동적이 객체에 대해서는 올바른 warping이 수행되지 않아 잘못된 손실값을 계산할 수 있다는 문제점도 있고, 정적인 영역임에도 불구하고 결국 RGB 이미지의 오차를 계산하는 photometric loss를 계산하는 것이기 때문에 textureless한 영역에 대해서는 잘못된 warping을 수행하더라도 낮은 loss 값을 계산하게 되어 이 역시도 학습에 방해가 되는 요소로 동작합니다.
그래서 SDE는 textureless한 영역에서 특히 부정확한 깊이를 추정한다거나 불연속적인 깊이를 추정하는 경우가 있다고 알려져있는데, 저자는 이 문제점이 발생한 가장 큰 원인으로 (photometric loss가 사실 가장 큰 문제이긴하지만 그건 self-supervised learning 특성상 어쩔 수 없으니 넘어가고) 기존 연구들이 point-to-depth 모델링을 고집하고 있기 때문이라고 주장합니다.
point-to-depth modeling이란 그냥 말그대로 RGB image 각 픽셀 하나하나를 곧바로 depth로 mapping하는 방식으로 학습하는 것을 의미합니다(아래그림참조)
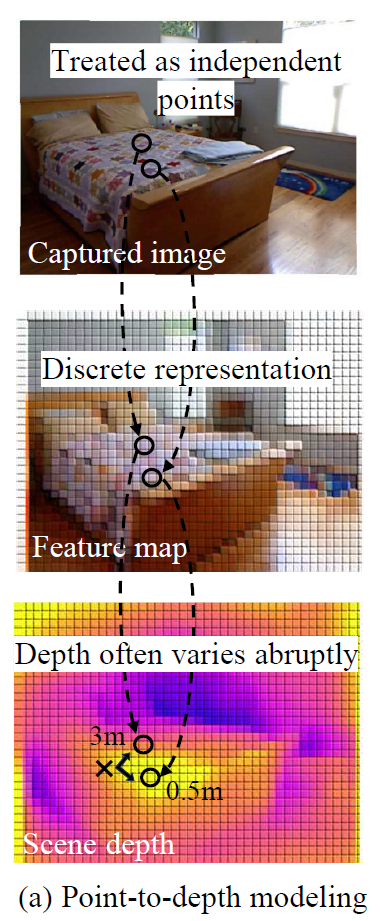
위와 같은 방식이 사실 픽셀 레벨의 예측 task에서 흔하게 사용하는 방식이긴하죠? 세그멘테이션도 그렇고 픽셀 하나하나를 개별적으로 보고 곧바로 깊이를 추정하는 방식은 예전부터 쭉 이어져온 흔한 방식이었습니다.
이렇게 각 픽셀들을 서로 독립적으로 보다보니 같은 region에 있는 픽셀들이 유사한 값을 가지는 것이 아닌 값이 튀는 현상들이 발생하였다고 저자는 주장합니다. 저자가 무슨 말을 하고 싶은지는 알겠는데 사실 위의 예시처럼 가까이 있는 픽셀의 깊이 값이 0.5m와 3m 같이 심하게 차이가 나는 경우는 별로 없다고 저는 생각하긴 합니다.
아무튼 유사한 평면에 있는 픽셀들끼리는 유사한 거리 값을 가져야한다는 기하학적 단서를 제공하기 위해 일부 연구들에서는 surface normal을 통해 평면에 대한 정보들을 활용하는 시도를 진행하였습니다. 즉 surface normal로 이웃 픽셀들이 local plane에 있다는 추가적인 정보를 제공하여 깊이 결과값들이 서로 닮도록 하고, 더 부드럽게 만들려고 하는 것입니다.
하지만 surface normal만을 plane indicator로써 사용한다는 것은 기하적대수학의 plane uniqueness 원칙을 위반하는 것이기에 신뢰성있는 접근 방식이 아니라고 저자는 주장합니다. 여기서 평면 유일성 원칙은 3D 공간 내 고유한 평면은 그 평면만의 고유한 normal vector와 offset을 가지고 있다는 것입니다. 조금 더 쉽게 풀어쓰면 3D 공간 상 평면을 Ax + By + Cz + D = 0의 방정식으로 나타낼 수 있는데 여기서 [A, B, C]를 법선 벡터, x, y, z를 평면 위의 3차원 점, D를 offset이라고 정의하기때문에, 유일무이한 평면은 법선 벡터만 또는 offset만을 가지고는 정해질 수 없다는 것이죠.
아무튼 기존 연구들은 법선 벡터만을 고려하고 offset은 함께 고려하지 않아 그 한계가 명확했다고 하며, 저자들은 point-to-depth 방식의 depth discontinuity issue 문제를 해결하기 위한 plane-to-depth 모델링 방식을 제안하였다고 합니다.
저자들의 방법론 컨셉은 같은 평면 내 모든 픽셀들은 고유의 파라미터로 표현될 수 있으며 이 고유한 파라미터들을 planar normal과 planar offset으로 명칭합니다. 그리고 이 planar normal과 planar offset을 통해 depth를 계산할 수 있으며 planar normal과 offset의 기하학적 특성을 적절하게 규제화해서 학습하면 동일 평면상 깊이들이 부드럽고 연속적인 값을 가질 수 있도록 강제할 수 있다고 합니다.
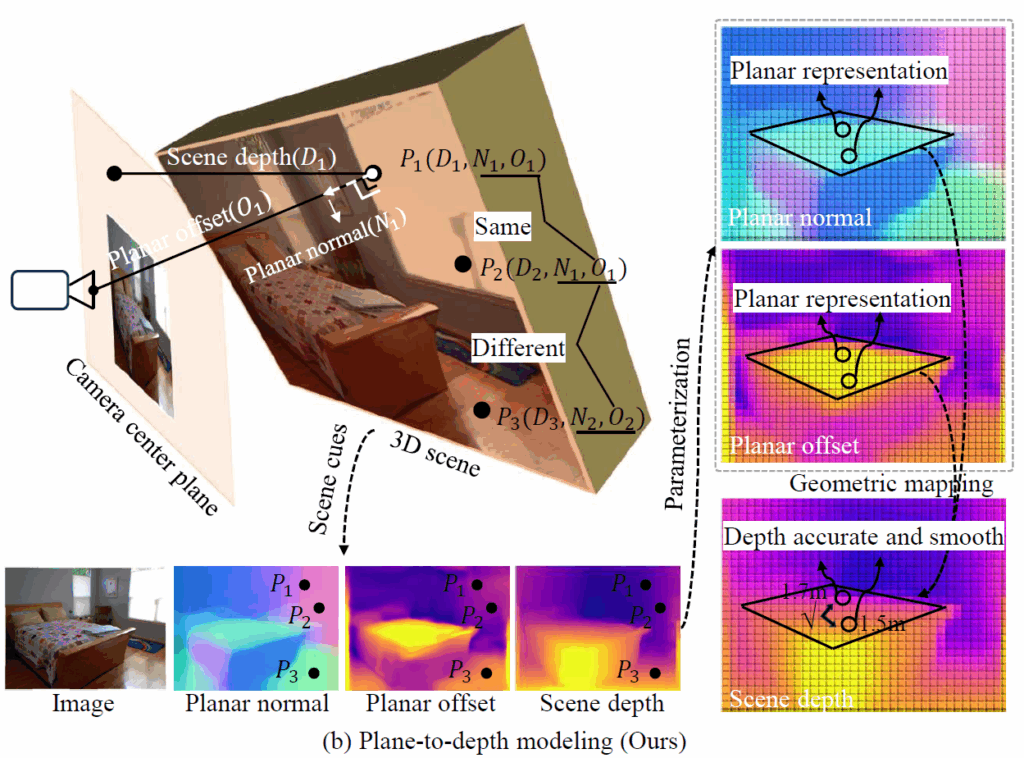
이러한 관점에서 저자들은 우선 평면에 대한 표현을 복원하기 위해 structured plane generation module이라는 것을 제안하였으며, 이 모듈은 spatio-temporal 기하학 단서들을 활용해 2개의 평면 특성들(i.e., planar normal & offset)이 근사화된 장면 구조를 복원하도록 가이드합니다. 그리고나서 그 평면 특성들을 평면 유일성 원칙에 근거하여 동일 평면 상 점들이 동일한 표현을 가지도록 최적화시켰다고 하네요. 저자들은 추가로 이러한 깊이의 불연속성이 low-texture region에서 자주 발생한다는 것에 착안해, photometricl loss가 낮은 지역을 잠재적인 깊이 불연속 영역으로 간주하고 이들을 따로 최적화하였다고 합니다.
이렇게 정리해서 말하면 무슨 말인지 잘 와닿지가 않죠? 저도 실제로 논문 인트로만 봐서는 이해하기 어려웠는데 밑에 방법론에서 각각에 대해 조금 더 자세하게 소개드리고자 합니다.
Plane-to-Depth Modeling
우선 해당 논문의 컨셉은 3D plane을 구성하는 평면 법선 벡터와 offset vector를 적극적으로 활용해 깊이를 예측하는 것입니다. 제가 아까 intro에서도 언급하긴 했는데 3차원 상의 평면을 법선 벡터와 offset으로 표현할 수 있다고 말씀드렸습니다 (Ax + By + Cx + D = 0 꼴).
그래서 어떤 3차원 공간 상의 한 장면은 여러개의 3D 평면으로 구성되어 있으므로 다음과 같이 표현할 수 있게 됩니다.
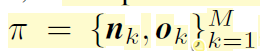
여기서 M은 평면의 개수를 의미하고 n과 o는 각각 평면의 법선 벡터와 offset 벡터를 의미합니다. 파이는 이 3차원 평면들의 집합을 의미하며 다른 말로는 3차원 scene으로 볼 수 있겠죠.
그리고 i번째 평면 위의 3차원 점 P가 있다고 할 때, n^{T}_{i}P = o_{i} 라는 식을 하나 세울 수 있습니다 (Ax + By + Cz = -D에서 [A,B,C]가 법선벡터, [x,y,z]가 3차원 점 P, -D가 offset vector o). 또 이 3차원 점 P를 이미지 평면으로 투영시켰을 때 2D point p = [u, v]^{T} 가 있다고 해봅시다.
그러면 이 2D point p와 3D point P는 K^{-1}(p*d) = P 꼴로 나타낼 수 있습니다. 여기서 K는 카메라 내부파라미터를 의미하며, d는 p지점에서의 depth값을 의미합니다 (P한테서의 z값).
자 그러면 해당 taks는 depth estiamtion이니 d값에 관심이 있는 것이므로 위에서 소개드린 수식들을 모두 활용해 아래와 같은 식으로 만들 수 있습니다.
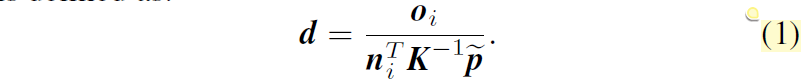
n^{T}_{i}P = o_{i} 와 K^{-1}(p*d) = P 를 활용해 depth d만 좌변에 남기고 나머지를 다 우변으로 넘기면 위의 수식1을 구할 수 있습니다.
동일 평면 상의 깊이들은 동일한 법선 벡터와 offset을 가지고 있기 때문에 사실상 depth의 variation은 pixel coordinate p에 의해 결정된다고 볼 수 있으며, 이는 다른 말로 하면 모델이 법선 벡터와 offset을 잘 예측하면 이와 관련된 depth를 도출해낼 수 있다는 것으로도 해석할 수 있습니다.
수식1은 한 point에 대한 것을 수식으로 나타낸 것이고 실제로는 이미지 전체에 대해 계산을 해야하니 수식1을 아래 수식2처럼 바꿔서 볼 수 있습니다.
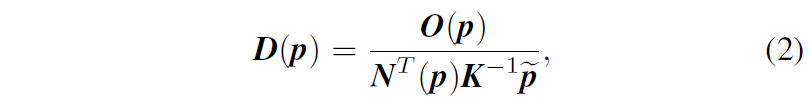
여기서 D, O, N은 모두 HxW의 spatial dimension을 가지게 됩니다.
Method
지금까지 plane의 특성들과 depth의 관계를 알아보았으니 이러한 관계를 저자들이 어떻게 활용해서 depth network를 만들었는지 그 방법론에 대해서 알아보겠습니다.
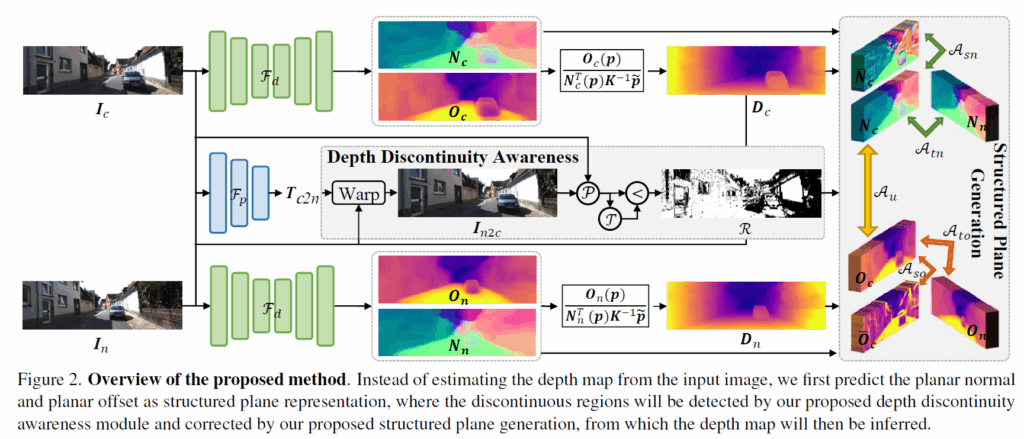
우선 그림2는 저자들이 제안하는 방법론의 학습 framework입니다. 여기서 I_{c}, I_{n} 이 존재하는데, c가 무슨 약자인진 모르겠지만 일단 target frame이라고 생각하시면 될 것 같고 n은 neighbor의 약자로 쓴 것 같습니다. 즉 이웃 프레임이라는 개념으로 target frame 기준 앞 또는 뒤 프레임을 의미한다고 생각하시면 좋겠습니다.
우선 기존 연구들이 RGB 이미지를 네트워크 F_{d} 에 태워서 곧바로 depth를 예측하던 것과 달리 저자들의 네트워크는 입력 영상에 대한 offset과 법선 벡터 map을 추정합니다.
이후에 해당 offset과 법선 벡터는 위에서 소개한 수식2를 통해 depth로 변환이 가능하며 저자들은 모델이 올바른 offset과 법선 벡터를 예측할 수 있도록 하기 위하여 이를 학습시키기 위한 과정을 제안합니다 (그림2 우측 Structured Plane Generation 과정)
Structured Plane Generation(SPG)
우선 SPG 과정은 크게 2가지로 planar normal alignment 과정과 planar offset alignment 과정으로 나누어져있습니다. 각 과정들에 대해서 하나씩 알아보겠습니다.
우선 normal alignment 과정입니다. 우선 예측된 depth값과 카메라의 내부파라미터 그리고 2d image coordinate를 활용해 3D point map을 생성합니다 ( P = DK^{-1}\hat{p} ).
그리고나서 아래 그림3 제일 좌측처럼 하나의 점과 그 점 기준 8개의 이웃 점들을 선택합니다. 그림3 좌측의 예시를 자세히 보면 제일 가운데 2d point를 p_{z} 라고 하고 y축으로 뻗은 점을 p_{zy} , x축으로 뻗은 점을 p_{zx} 라고 해봅시다. 3D point상에서는 small p를 Large P로 표현가능합니다.
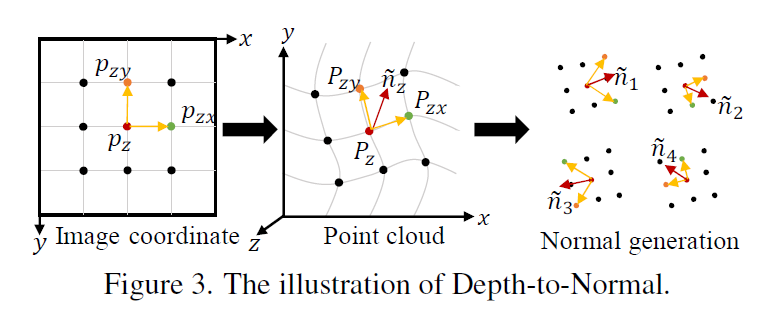
그럼 이제 중심점 P_{z} 에서 P_{zy} 방향으로 가는 벡터, 그리고 P_{zx} 방향으로 가는 벡터가 있다고 했을 때 두 벡터에 대한 외적을 통해 normal vector를 계산할 수 있습니다.
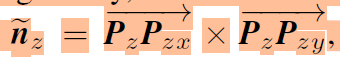
그림3 우측과 같이 중심점과 그 이웃 점 8개를 활용해 총 8가지의 normal vector를 계산할 수 있으며 저자들은 normal vector의 강인성을 위해 4개정도의 normal vector를 계산한 후 이에 대한 평균을 계산하여 해당 지점의 대표 normal vector를 계산합니다.
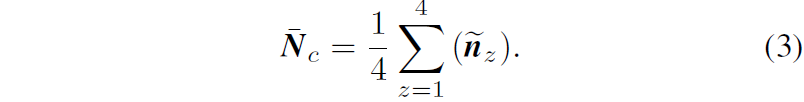
이렇게 대표 법선 벡터를 계산하게 되면, 이 대표 법선 벡터와 모델이 예측한 법선 벡터가 서로 같아지도록 아래와 같은 목적함수를 설계합니다.
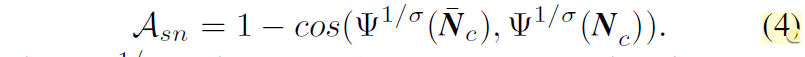
여기서 저 삼지창?은 down sampling function을 의미하며 sigma 값은 downsampling rate를 의미합니다. 우선 수식4의 목적은 결국 두 법선 벡터가 향하는 방향이 같으면 두 벡터 사이의 각도가 0이므로 cos 0은 1의 값을 가지게 되는 것이고 따라서 1-1은 0을 유도하는 것으로 두 법선 벡터가 같은 방향을 가지도록 학습하는구나 라고 이해하시면 좋겠습니다.
또한 원본 해상도에서 해당 loss를 계산하는 것이 아닌 일정 수준 다운샘플링을 하고나서 수식4의 loss를 계산하는데 저자들은 이렇게 다운샘플링을 함으로써 경계면에 대한 픽셀들의 영향력을 완화시킬 수 있었다고 합니다.
지금까지는 target frame에서만 계산되는 spatial 축에서의 규제를 알아보았으며 저자들은 앞뒤 프레임을 활용한 temporal 축에서의 normal alignment도 함께 진행합니다.
우선 target view에서 관측한 이웃 view의 법선 벡터는 두 view 사이의 카메라 회전 행렬을 통해 아래와 같이 계산이 가능합니다.
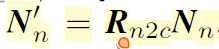
그다음에 저자들은 아래 수식을 통해 N'_{n} 을 target view로 warping시켰다고 합니다.
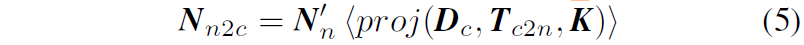
수식5번에서 카메라 내부 파라미터, 두 view에 대한 상대적인 카메라 포즈, 그리고 target view의 depth map을 통해 source view에서의 정보를 target으로 warping하는 것은 SDE의 핵심 과정이긴한데 저는 수식5보다는 그 위에 N_{n}이 아닌 N'_{n} 을 따로 만들어 warping을 한 방식에 대해서 아직 이해가 어렵네요.
아무래도 저 <proj> 과정은 source 2d cooridnate에서 target 2d coordinate로 좌표계를 변환하는 것일 뿐 법선 벡터가 의미하는 방향 자체를 바꾸는 것은 아니다보니 법선 벡터의 방향도 target view에서 관측하였을 때의 방향으로 바꿔주기 위해 rotation을 곱한건가 생각하고 일단 넘어가겠습니다.
아무튼 이렇게 수식5를 통해서 source view에서 추론한 법선 벡터를 target view로 옮겼으니 이제 실제 target view에서 추론한 법선 벡터들과의 유사도를 계산해야합니다. 이론상으로는 둘이 같은 법선 벡터이므로 동일한 방향을 가지고 있어야 하기 때문에 역시나 둘의 cos값은 1임을 이용한 목적함수를 사용합니다.
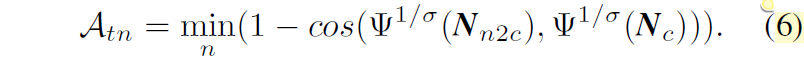
이 수식4와 6을 통해 planar normal alignment loss는 아래와 같이 구성될 수 있습니다.
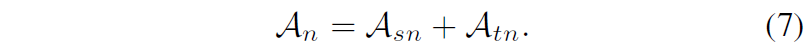
자 그럼 다은 차례는 Planar Offset Alignment에 대한 것입니다.
우선 만약 target view에서의 평면 법선 벡터 \bar{N}_{c} 와 추론된 Depth D_{c} 가 있다고 하였을 때, 수식2를 응용해서 아래와 같은 식을 나타낼 수 있습니다.
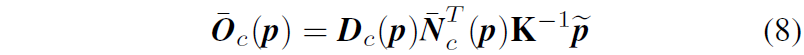
수식8을 통해 대표 offset \bar{O}_{c} 를 계산하였으니, spatial offset alignment는 아래 수식으로 계산 가능합니다.
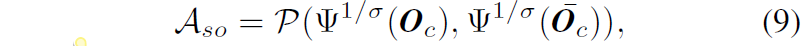
offset은 방향을 나타내는 vector 개념보다는 말그대로 원점에서 평면 사이의 거리를 나타내는 상수에 해당하기 때문에 기존의 L1 loss와 SSIM loss가 섞인 photometric loss를 그대로 활용해주는 모습입니다.
이 offset을 temporal 축에 대해서도 alignment를 진행해주어야합니다. 앞에서 법선 벡터는 source frame n에 대한 법선 벡터를 warping 연산을 통해 target frame c로 옮기고 비교를 해준 반면, offset은 오히려 target frame을 source frame으로 변환하는 방식으로 접근을 합니다.
구체적으로, 우선 target frame c에서 추론한 Depth D_{c} 를 warping하여 source frame에서 관측된 depth D'_{n} 로 바꾸고 source frame n에서 예측한 법선 벡터를 통해 아래와 같이 source frame에서의 offset을 계산할 수 있습니다.
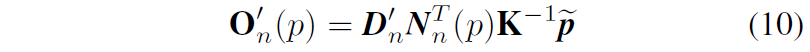
그리고 저자들은 모델이 직접 source view에서 예측한 offset O_{n} 을 바로 사용하는 것이 아니라 아래 수식과 같이 warping 과정을 한 뒤 O'_{n} 과의 비교를 계산합니다.
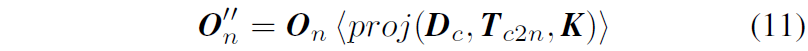
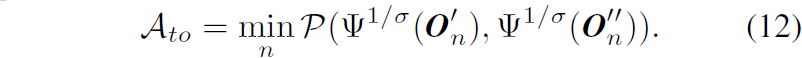
근데 제가 사실 이 수식11번의 과정에 대해서는 도저히 이해가 안되더군요. 저자들이 논문에서는 딱 한줄로 O_{n} 을 곧바로 사용하지 않고 수식11과 같이 사용한 이유에 대해 warping flow가 pixel grid에 lie하지 않기 때문이라고만 적혀있는데 이 문장 자체도 무슨 말인지 모르겠으며 애초에 저 warping을 수행하게 되면 source view image와 정확히 픽셀레벨로 일치하는 offset map을 target view image와 픽셀레벨로 정합시키게 되거든요.
근데 수식 10을 통해 계산된 O'_{n} 은 여전히 source view와 align된 값이기 때문에 둘 사이의 직접적인 비교가 불가능하다고 저는 생각을 하는데.. 논문에서 말하는 저 proj 함수가 정확히 어떻게 동작하는지 논문 내에서는 자세한 소개가 없고 그냥 기존의 SDE에서 사용되는 warping이다라고 한다면 제가 말하는 방식이 맞아서 문제가 발생할 것 같다는 생각만 드네요. 아무튼 이 부분은 제 머리로는 이해가 안돼서 넘어가야될 것 같습니다.
결과적으로 offset alignment 역시 spatial 축과 temporal 축에서 각각 진행이 되며 아래로 정리가능합니다.
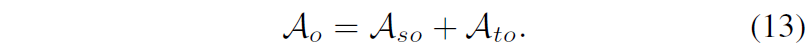
그리고 저자들은 동일 평면 내 존재하는 픽셀들의 평면 법선 벡터와 평면 offset이 모두 유사해아하기 때문에 아래와 같은 1차 기울기 값이 커지지 않도록 loss를 추가하였다고 합니다.
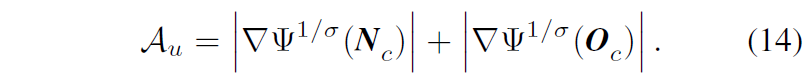
근데 저것도 평면과 평면이 바뀌는 지점(즉 전경과 배경의 경계부분) 등에서는 기울기 값이 커져야하는게 맞아서 그런것들을 고려하여 계산을 해야할 것 같은데 일단 그런 부분 고려없이 싹다 규제화를 한 것 같습니다.

결과적으로 저자들의 이러한 loss term과 규제화 덕분에 법선 벡터와 offset이 보다 더 정확해졌다고? 저자들은 주장합니다.
Depth Discontinuity Awareness
다음은 Depth의 불연속성을 찾는 모듈에 대한 소개입니다. 인트로에서도 잠깐 소개드렸는데 photometric loss의 특성상 textureless region에서는 정확한 loss를 계산할 수 없고 이래서 depth가 부정확하게 학습이 될 수 있다고 말씀드렸습니다.
그래서 저자들은 이 영역들을 찾아내서 refinement해주고 싶어했는데 우선 찾는 과정은 매우 단순합니다. 그냥 아래 수식15처럼 photometric loss를 계산한 다음에 일정 threshold 이하 값이 나오는 영역을 찾는 것입니다.
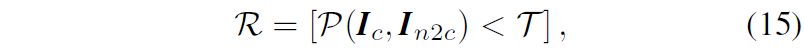
즉 photometric loss가 이 임계치보다 낮으면 참값을 가지고 아니면 false 값을 가지게 되며 참값을 가진 영역을 깊이가 불연속적이다라고 그냥 가정해버리는 것이죠.
근데 이 방식이 솔직히 좀 너무 단순하기도 하고 저자의 의도대로 동작하기 어려울 수 있긴 합니다. 실제로 모델이 정확하게 깊이를 예측해서 photometric loss가 낮게 나온 걸 수도 있잖아요. 근데 일단 그런 고려는 빼버린 것 같고 대신에 저자들은 임계치를 하나의 단일 값이 아닌 여러가지 variation을 두어서 사용하게 되는데 그냥 photometric loss의 평균값을 임계치로 사용했다고 합니다.
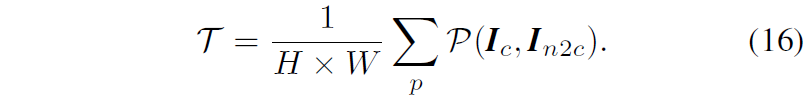
즉 모델이 학습을 점점해서 정확한 depth를 뽑으면 photometric loss의 평균 값이 점점 작아질테니 임계치도 함께 더 낮아지도록 설정하는 것인데 솔직히 이것도 너무 단순하지 않나..? 싶네요.
아무튼 이렇게 생성된 마스크 R값은 SPG 모듈에서 활용된다고 하는데 솔직히 말씀드리면 어떻게 활용된다는건지 논문에서 안나와있네요..? 그냥 곱하면 되는건지.. 뒷부분으로 갈수록 논문이 너무 불친절해서 당황스럽습니다.
Experiments
평가 데이터셋은 KITTI와 Make3D, NYU와 ScanNet을 사용하고 KITTI와 NYU가 학습 및 평가를 하는 메인 dataset, Make3D와 ScanNet은 generalization을 위해 평가만 수행하는 데이터셋입니다.
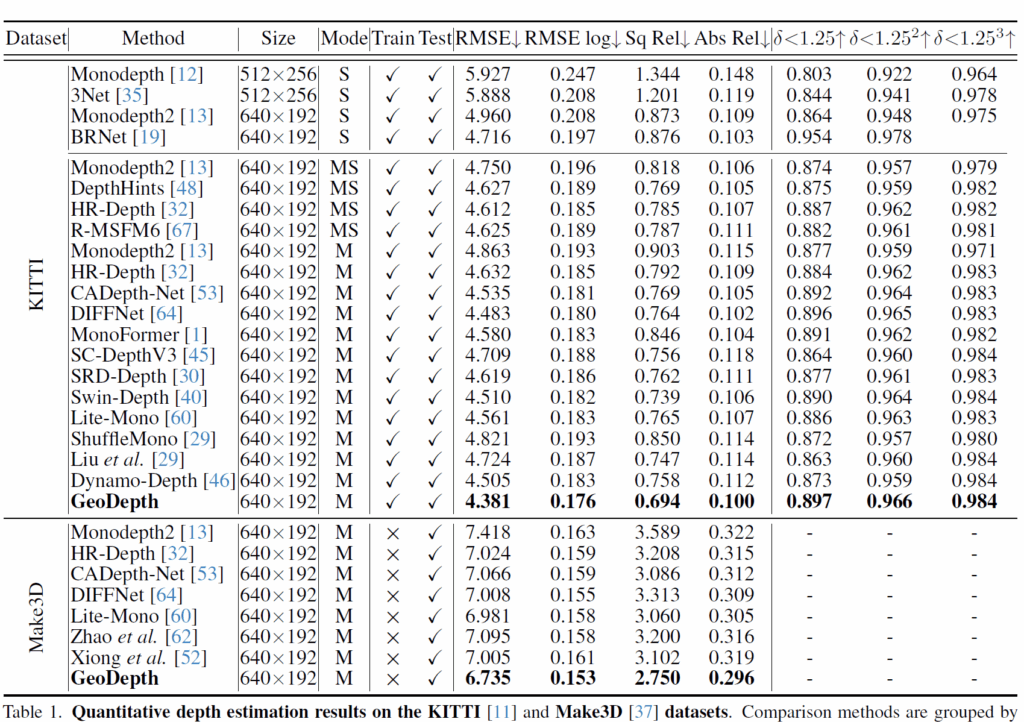
우선 KITTI dataset에 대한 정량적 결과입니다. 보시면 자신들이 가장 좋다고 하네요. 근데 사실 자신보다 좋은 성능의 방법론들은 테이블에 넣지 않아서 자기가 가장 좋은것처럼 보이는 겁니다. KITTI dataset에서 SCDepth v3라는 방법론이 언급되는 것을 볼 수 있는데 아래 NYU 평가테이블에서는 SCDepthv3 방법론이 빠진 것을 확인하실 수 있습니다.
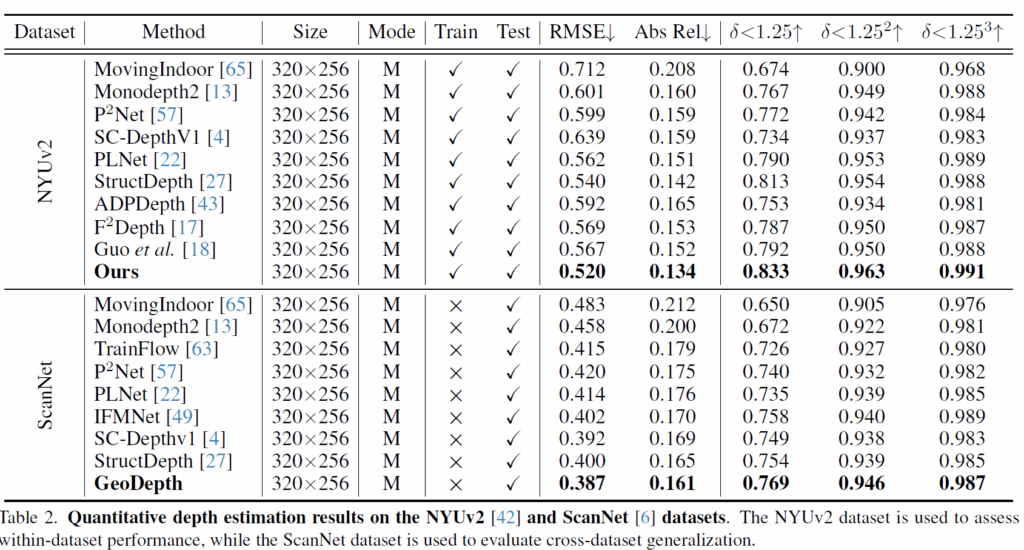
이는 SCDepthV3가 NYU에서 저자들의 GeoDepth보다 성능이 더 좋기 때문에 그래요. 얘네가 자기보다 더 좋은 성능을 가지는 방법론은 다 빼버려서 SOTA인 것처럼 하더라구요. 25년에도 아직 이렇게 논문을 쓰고 있다는 점에서 안타까운 현실입니다.
다음은 Ablation study입니다. KITTI dataset에서 ablation한 것으로 보이고 Baseline 대비해서 저자들의 각 모듈 하나하나가 보여주는 성능 향상 폭이 그리 크지는 않은 것 같습니다만 다 합쳤을 때 그래도 조금의 성능 개선이 있는 모습입니다. 그리고 파라미터 수도 크게 늘어나지도 않구요.
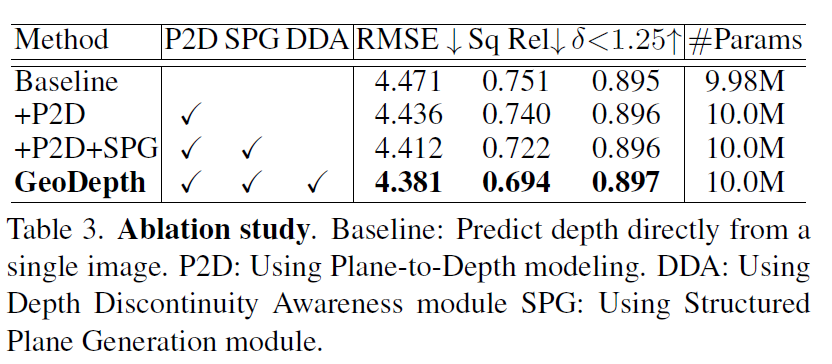
결론
솔직히 말해서 제가 리뷰어라면 reject 줬을 논문입니다. 근데 이쪽 분야 논문을 잘 모르는 리뷰어라면 테이블 결과만 보고 성능이 가장 좋은 걸로 착각하고 매우 좋게 봤을 것 같아요. 실제로 기존 연구들과 달리 depth 예측을 offset과 법선 벡터로 진행한다는 점에서 접근 방식에 대한 novelty만큼은 상당히 있다고 저도 생각합니다.
컨셉이 흥미로웠다는 점에서만 만족하고 넘어가야될 것 같네요. 저자들이 그토록 강조했던 depth의 불연속성이 잘 해결되었는지 이런 부분에 대한 평가도 딱히 고려하지 않았고 성능 향상도 ablation 살펴보니 엄청 높지는 않았던 것 같아서.. baseline을 애초에 좋은 걸 써서 시작했다는 기분만 드는게 아쉽네요.
안녕하세요 정민님, 불친절한 논문에서 구체적인 리뷰 감사합니다.
뭔가 SOTA는 아니라곤 하지만 CVPR이 아니라면 저자의 방법론이 더 확장될 가능성이 있다 생각하는지 궁금합니다.
그리고 궁금한게 여러 평면들의 파라미터들을 (a,b,c,d) 구하는거라면 저게 단일 이미지로 유사 3D reconstruction을 하고 있는게 아닌가 싶은데, 제 짧은 지식으로 뇌피셜을 작성해보면 3D reconstruction model중 좋은거를 teacher로 두고 이 monocular image를 넣어서 나온 초평면들을 3D map으로 생각하고 teacher map을 따라가게 만들어서 depth 추정을 하게하는 것이 어떨지.. 단순히 궁금증이 생겨서 여쭤봅니다. 감사합니다.
안녕하세요. 댓글 감사합니다.
우선 저자의 방법론은 self-supervised monocular depth estimation task뿐만 아니라 다른 depth estimation task에서 충분히 활용 가능하다고 생각합니다.
말 그대로 depth를 곧바로 예측하는 것이 아닌 평면의 법선 벡터와 offset으로 나눠서 예측하고 이를 통해 depth를 도출하자는 방식이라서 depth를 추론해야하는 상황에서는 어디든 활용이 가능하기 때문이죠.
그리고 2번째 질문에 대해서는 우선 reconstruction 기법들도 다양하고 그와 관련된 모델들도 다양해서요. 3D recon쪽 연구들이 보통 object에 대한 다양한 multi-view를 찍거나 방 같은 특정 공간 내에서의 recon을 위주로 하다보니 그런쪽 모델은 부적합할 것 같고 outdoor의 sequence를 recon하는 방법론은 활용 가능할 수는 있겠으나 해당 모델들도 이미지 하나만 입력받아서는 reconstruction이 따로 안되지 않나 싶네요 그냥 depth map 자체를 예측하는 depth model 처럼 동작할 것 같아서요.
결국 인택님의 질문은 3d reconstruction model이라기보다는 depth network를 teacher model로 삼아서 distillation하는 방식으로 볼 수 있고 그 관점에서는 당연히 적용 가능하다고 볼 수 있겠습니다.
안녕하세요 정민님, 어려운 논문이지만 쉽게 설명해주셔서 감사합니다.
질문이 하나 있는데, 말씀해주신것처럼 소개해주신 논문의 프레임워크 설계 아이디어가 새롭고 복잡한것같습니다.
딥러닝 모델을 통해 좋은 데이터만 제공된다면 올바른 뎁스를 예측하도록 설계된 네트워크도 많은것 같은데, 이러한 이론 기반 설계가 실제로 유의미한지 궁금합니다. 논문에서 실험으로 제시한 성능이 획기적으로 높지는 않는데, 일반적으로 새로운 접근으로도 성능 향상이 미미한 경우가 많은지 궁금하네요.
감사합니다.
댓글 감사합니다.
우선 해당 방법론도 딥러닝 모델 기반으로 학습 및 추론되는 방법론이라는 점 말씀드릴 수 있겠으며 그저 입력 x와 그에 대응되는 y를 모델한테 줘서 학습하는 방식보다는 y를 추론하는데 있어 도움이 되는 이론적 개념들이 있으면 그 개념을 모델 추론 과정에 최대한 모델링해서 넣는 것이 당연히 유의미하다고 저는 생각을 합니다.
그리고 두번째 질문에 대해서는 따로 드릴 말씀이 없네요. 이것저것 시도하다가 성능이 크게 좋아질 수도 있는거고 반대로 떨어질 수도 있는 것이 딥러닝 아닐까요? 허허.