[arXiv 2025] Perfecting Depth: Uncetrainty-Aware Enhancement of Metric Depth

안녕하세요, 69번째 x-review 입니다. 이번 논문은 arXiv 2025년도에 올라온 Perfecting Depth라는 논문 입니다.

그럼 바로 리뷰 시작하겠습니다 !

1. Introduction

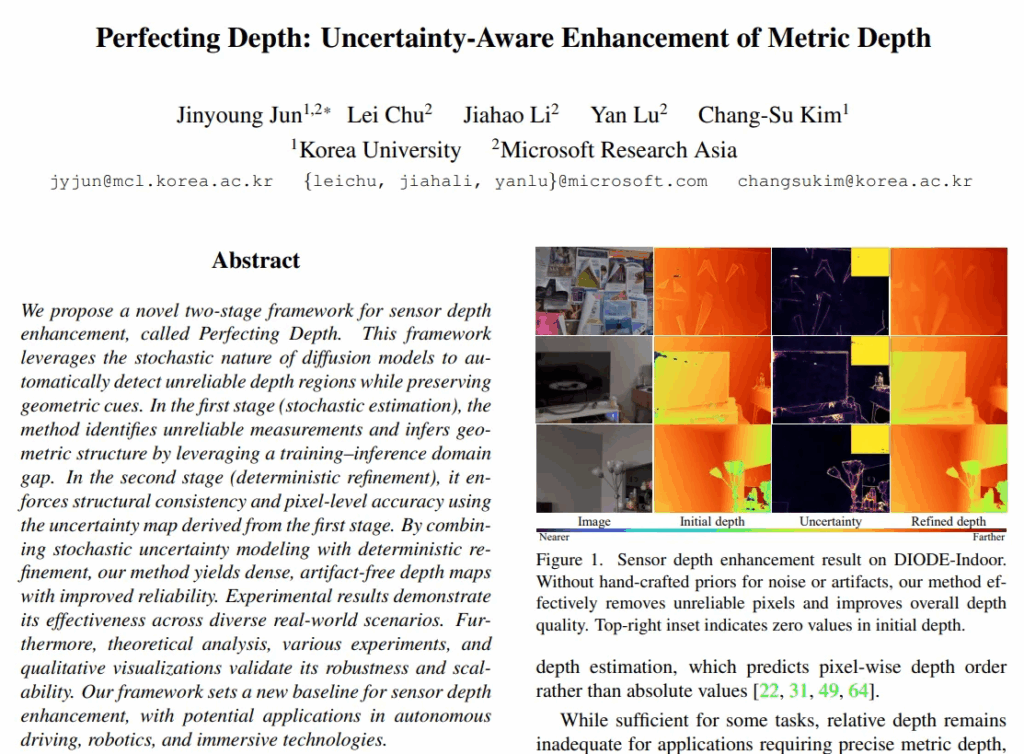
monoculdar depth estimation(MDE)는 아주 초기에는 metric depth를 예측하는데 초점을 맞추었습니다. 하지만 특정 센서로 취득한 각각의 데이터셋에 대한 의존도가 높아서 실제 application에 적용하기에 한계가 있었다고 합니다. 그래서 그 이후로 metric이 아닌 relative depth를 메인으로 연구가 진행되고 있습니다. 일부 task들에서는 relative depth만으로도 충분할 수 있지만, 로봇이나 3D reconstruction 등 정확한 depth 값들이 필요한 작업에는 적절하지 않습니다. 그렇다고 metric depth를 제공할 수 있는 depth 센서 값을 사용하자니 Fig.1에서 보이는 것과 같이 노이즈가 발생하여 성능을 저하시키기 때문에 그대로 사용하기에는 어려움이 있죠.

그래서 본 논문에서는 센서의 depth를 개선하기 위해 Perfecting Depth라는 프레임워크를 제안합니다. 기존 방법론들은 미리 하나하나 정의해놓은 규칙(artifact prior)를 이용해서 센서의 depth를 개선하려고 했는데요, 본 논문에서는 diffusion 모델의 확률적 특성을 이용해서 각 픽셀의 신뢰도를 자동으로 평가할 수 있도록 하였습니다. 이를 위해 학습과 inference 사이에 일부러 차이를 주었다고 하는데요, 학습에서는 합성 데이터로 diffusion 모델을 학습하고 inference에는 노이즈가 있는 실제 센서의 raw depth를 사용했다고 합니다. 이렇게 의도적인 차이를 주면 모델이 픽셀 각각에 대해 얼마나 신뢰할 수 있는지, 불확실성과 기하학적인 정보를 평가할 수 있게 한다고 합니다.

이러한 의도를 가진 본 논문의 모델은 크게 2가지 단계의 파이프라인으로 구성되어 있습니다.

첫번째는 stochastic estimation 단계로, 같은 입력에 대해 여러 번 diffusion 과정을 반복해서 여러 개의 depth map 샘플을 생성합니다. 각 픽셀에 대해서 평균과 분산을 계산해서 분산이 큰 픽셀은 신뢰도가 낮은 영역으로 판단합니다.

두번째 deterministic refinement 단계는 1단계에서 얻은 픽셀 단위의 신뢰도를 가지고 신뢰도가 낮은 영역을 개선하는 단계 입니다. 이 때, diffusion 과정에서 나온 여러 정보들을 종합해서 guidance feature를 구성하고 이를 기반으로 정확한 depth map을 생성하게 됩니다.

더 자세히는 method에서 살펴보도록 하며, 본 논문의 main contribution을 정리하면 다음과 같습니다.

1. 센서에서 취득하는 depth를 개선하기 위해 handcraft prior 없이 노이즈를 찾을 수 있는 diffusion-deterministic 파이프라인을 제안
2. 학습 때 사용한 합성 데이터가 아닌 실제 real 센서 데이터에 대해서 높은 일반화 성능 달성
3. 센서 노이즈 제거나 depth completion 등 다양한 시나리오에서 SOTA를 달성

2. Method

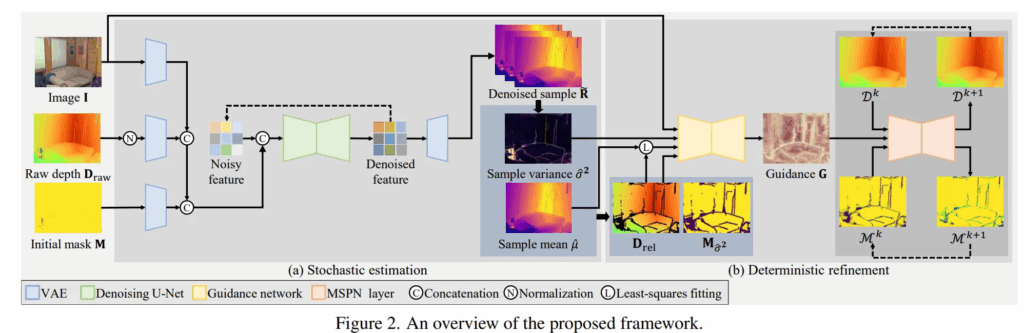
RGB 이미지 I \in \mathbb{R}^{3 \times H \times W}와 raw depth D_{raw} \in \mathbb{R}^{H \times W}가 입력으로 들어가면 노이즈가 없는 dense depth map D_{refine}을 생성하는 것을 목표로 합니다.

이 때 D_{raw}는 하드웨어 자체의 한계와 투명한 물체 등의 표면에 대해서 노이즈가 발생하여 일부 픽셀에 신뢰할 수 없는 값을 가지게 됩니다. 이러한 현상을 논문에서는 식(1)과 같이 정의하였는데요,

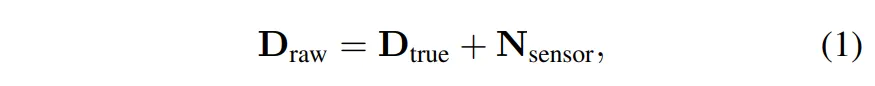
• N_{sensor} : 센서에서 발생하는 노이즈

N_{sensor}는 특정한 분포에 따라 규칙적으로 발생하는게 아니기 때문에 가우시안과 같은 기존의 방식으로 모델링 하기가 어렵다는 한계가 있습니다.

그래서 Fig.2와 같은 프레임워크를 제안하는데, 인트로에서 말씀드린 것처럼 크게 stochastic estimation / deterministic refinement 2단계로 구성되어 있습니다.

2.1. Stochastic estimation

1단계는 유저가 직접 artifact prior, 즉 노이즈 패턴 등을 정의하지 않고 모델이 각 픽셀의 불확실성을 자동으로 판단하는 것이 목적 입니다.

이를 위해 확률적 특성을 가진 diffusion 모델 \boldsymbol{\Theta}를 사용합니다. 식(2)는 diffusion 모델의 condition 기반 학습을 정의한 것 입니다.

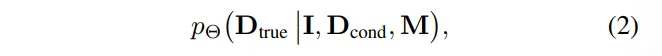
• D_{true} : GT
• D_{cond} : 조건으로 사용하는 depth map
• M : 마스크

GT에 대해 랜덤하게 마스크 M을 생성해서 M \otimes D_{true} 연산을 통해 D_{cond}을 만듭니다. 그렇게 해서 D_{cond}와 RGB 이미지를 같이 사용해서 depth를 복원하는 diffusion을 학습하는 것이죠. 학습할 때 이렇게 깨끗한 depth만으로 학습하는 이유는 현실적으로 다양한 노이즈나 결함을 미리 모두 정의해서 학습하기에는 어려움이 있습니다. 그래서 학습은 깨끗한 합성 데이터만을 사용하고, inference 때는 노이즈가 있는 raw depth를 넣는 것이죠. 이렇게 차이를 주어 모델이 어떤 픽셀이 신뢰도가 낮은지를 스스로 판단하게 됩니다.

추론 때는 raw depth D_{raw}가 diffusion 모델에 condition으로 입력됩니다. diffusion denoising을 N번 반복하는데, 반복할 때 마다 다른 랜덤 노이즈에서 시작해서 서로 다른 복원 결과인 \tilde{R}_i를 얻습니다. 각 복원 결과에 대해 식(4)와 같이 두 가지를 계산합니다.

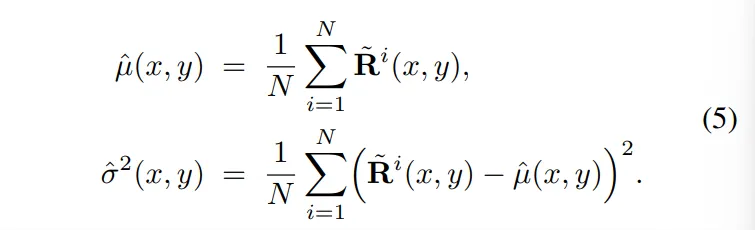
식(4)에서 계산한 평균, 분산으로 식(5)와 같이 전체 평균 분산을 계산하는데요, 이때 \hat{\sigma}(x,y)는 해당 픽셀의 불확실성으로 정의됩니다. 불확실성이 크면 N번 반복한 복원 결과가 들쭉날쭉으로 나와서 신뢰도가 낮음을 의미합니다. 반대로 불확실성이 작으면 예측 결과가 안정되어서 신뢰도가 높다고 간주할 수 있습니다.

이렇게 픽셀 레벨에서의 분산을 신뢰도로 사용할 수 있는 이유에 대해 베이시안 관점에서 추가적으로 설명하는데요, 베이시안 확률이 현재 아는 정보를 가지고 어떤 게 가장 가능성이 높은 결과인지를 계산하는 방식이잖아요. 이를 따라 논문에서는 픽셀 단위로 지금 RGB 이미지와 센서 depth 값을 봤을 때 진짜 depth 값이 무엇일지에 대한 가능성을 계산하려는 것 입니다.

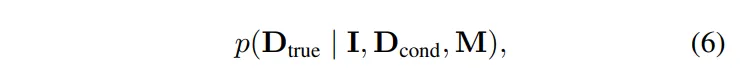
식 (6)은 RGB 이미지와 condition으로 주어지는 depth 마스크를 기반으로 실제 epth 값의 가능성 분포를 나타냅니다. 이를 픽셀 레벨로 보면 식(7)과 같습니다.

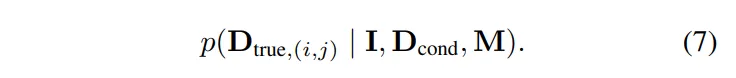
그럼 식(7)은 해당하는 픽셀의 실제 depth가 어떤 값인지에 대한 확률적인 분포를 알 수 있는 것이겠죠. 그리고 이러한 확률을 식(8)과 같은 베이시안 정리를 적용한 것 입니다.

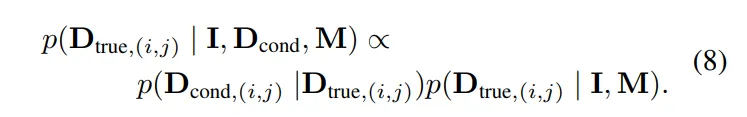
식(8)은 두 부분으로 나누어서 볼 수 있는데, 먼저 p(D_{cond, (i,j)} | D_{true,(i,j)})는 LIklihood 입니다. 즉, 센서에서 측정한 값이 진짜 값과 얼마나 잘 맞는지를 나타냅니다. 잘 맞을 수록 해당 값이 커지게 되죠. 그 다음 (p(D_{true,(i,j)} | I,M)은 prior 입니다. RGB 이미지와 마스크를 보고 그럴듯한 depth 값이 무엇일지 모델이 학습한 knowledge를 반영한 확률 입니다. 센서에서의 정보가 부족하면 모델은 해당 prior에 더 의존하게 되는데, 이게 확실하지 않아서 분산이 커집니다.

결국 센서 값이 신뢰할 수 있으면 likelihood가 커지고 분산이 작아집니다. 반대로 센서 값이 이상하면 prior에 의존해야 하고 분포가 들쭉날쭉해져서 분산이 커지기 때문에 저자는 이러한 분산을 신뢰도의 척도로 사용할 수 있다고 말하는 것 입니다.

diffusion 모델을 여러 번 반복해서 나온 복원 결과의 분산을 보고 어디가 신뢰할 수 있고 어디가 그렇지 않은 지를 알 수가 있습니다. 이를 기반으로 신뢰할 수 있는 영역은 그대로 두고, 분산이 큰 영역만 골라서 개선하하며 이 개선은 deterministic 모델을 통해 더 정확하게 처리했다고 합니다.

Remarks

논문에서 처음에는 depth에서의 누락된 영역을 다른 아티팩트와 따로 다루고 있습니다. 왜냐하면 누락되는 영역은 값이 0이거나 비어있기 때문에 찾아내기가 굉장히 쉬워서 복잡한 계산 없이도 마스크만으로도 감지할 수 있어서 cost가 낮기 때문 입니다. 그런데 수식적으로만 보면 이 두 개가 매우 비슷한데요, 식(8)에 따르면 누락된 영역이나 아티팩트 모두 likelihood가 작고 prior에 더 많이 의존을 한다는 것 입니다. 그도 그럴 것이 누락된 영역이어도 센서 값이 아예 없어서 무효한 값이라 liklihood가 거의 0일 것이고, 아티팩트도 센서 값이 틀리거나 애곡되어 likelihood가 낮을 것 입니다. 즉 두 케이스 모두 확률이 거의 prior에 의존하고 분산이 커진다는 공통된 현상을 보입니다. cost의 차이로 분리해서 정의했었는데 수식적으로 정리해보니 동일한 cost로 한번에 \sigma^2가 큰 경우를 통해 찾을 수 있다는 것이죠. 그래서 \sigma^2 기반의 필터링을 통해서 신뢰할 수 없는 픽셀(누락된 영역과 아티팩트 둘 다)를 걸러내어 불확실한 영역만 개선 단계로 보낸다고 합니다.

2.2. Deterministic refinement

diffusion 모델은 학습할 때 depth 값을 [-1, 1] 범위로 정규화를 하는데요, 따라서 diffusion 모델의 출력값은 실제 metric 스케일이 아닙니다. 또한 diffusion은 글로벌한 영역에 대한 확률적 특성을 가지고 있기 때문에 로컬한 픽셀 각각에 대한 디테일한 보정에는 한계가 있다고 합니다.

그래서 이 refinement 네트워크는 정규화된 depth 값을 실제 미터 단위로 변환하고, 픽셀 레벨에서 값을 정밀하게 보정하는 것을 목적으로 합니다. 베이스로 삼은 프레임워크는 SDR(sparsity-adaptive depth refinement)라고 합니다.

SDR은 기본적으로 RGB 이미지를 통해 얻은 MDE 결과를 바탕으로 sparse한 depth 값을 가지고 나머지를 보정하는 프레임워크라고 합니다. 가장 핵심은 masked spatial propagation이라고 해서 신뢰할 수 있는 depth에서 시작해서 인접한 이웃 픽셀로 점차적으로 값을 개선해나가는 방식 입니다. 이 propagation은 마스크에 따라 달라지고 신뢰도가 높은 픽셀을 중심으로 진행한다고 하네요.

이러한 SDR을 본 논문에서는 어떻게 이용하냐면, diffusion 단계에서 얻은 \hat{\sigma^2}를 기반으로 신뢰할 수 있는 픽셀부터 시작해서 주변 픽셀로 개선된 depth를 propagation 합니다. sparse한 metric depth를 이용하기 때문에 메트릭 스케일로 복원할 수 있고 픽셀 단위로 정확도 역시 향상시킬 수 있다고 합니다.

해당 과정에 대해서 수식적으로 살펴보도록 하겠습니다.

가장 먼저 diffusion 결과에서 2.1.에서 이야기한 것과 같이 신뢰도 마스크를 정의합니다.

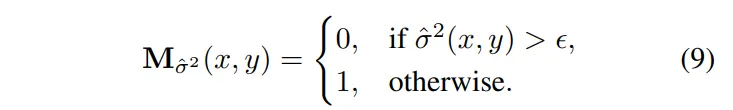
• \hat{\sigma^2}(x,y) : 해당 픽셀의 분산값
• \epsilon : 신뢰도를 기준으로 한 임계값

식(9)와 같이 정의한 마스크는 분산이 낮은(=신뢰할 수 있는) 픽셀만 1로 표시를 하게 됩니다.

이 마스크를 사용해서 신뢰할 수 있는 값들로 이루어진 depth map을 구성합니다.

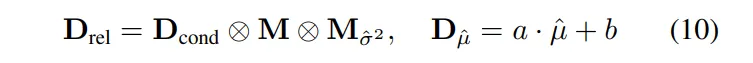
• M : 기존의 depth 마스크
• M_{\sigma^2} : 이번에 정의한 신뢰도 마스크
• D_{rel} : 센서 값 중에서 신뢰할 수 있는 값만 남긴 depth map

식 (10)의 D_{\hat{\mu}} 는 diffusion 샘플의 평균 값을 가지고 스케일 조정을 한 값으로, 정규화된 예측 값(relative depth)를 metric depth로 보정한 depth map을 의미합니다. 이 때 스케일과 shift a,b는 일반적인 least-squares 방식으로 구할 수 있습니다.

위에서 구한 값들을 이용해서 refinement를 위한 입력 feature를 식(12)와 같이 구성합니다.

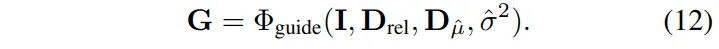
I, D_{rel}, D_{\hat{\mu}}, \hat{\sigma^2}를 입력 feature로 합쳐서 refinement 네트워크에 넣기 전의 guidance feature G를 생성하는 것 입니다. D_{rel}은 확실하게 믿을 수 있는 depth 값을 가지고 있고, D_{\hat{\mu}}는 전체적인 구조적 정보를 반영하고 있으며, 마지막으로 \hat{\sigma}}^2는 픽셀마다의 신뢰도이기 때문에 이 세 가지를 통해서 정확성과 구조적인 일관성을 동시에 가질 수 있을 것이라고 생각한 것 입니다.

그럼 이제 refinement를 어떻게 하는 지에 대해서 살펴보겠습니다.

첫번째는 식(13)과 같이 정의한 초기화 단계 입니다.

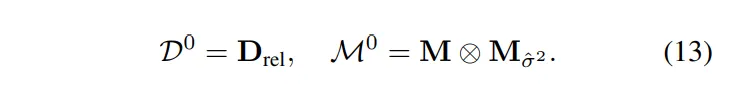
\mathcal{D}^0은 신뢰 가능한 raw depth 값만 포함된 초기 depth map이고, \mathcal{M}^0은 두 마스크의 곱을 의미합니다. 즉 센서값이 유효하면서 신뢰도도 높은 픽셀만을 포함하고 있습니다.

이렇게 초기화한 값에 대해서 반복적인 refinement를 진행합니다.

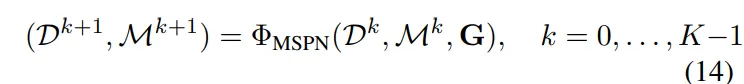
• \boldsymbol{\Phi}}_{MSPN} : masked spatial propagation 네트워크

초기 depth를 시작으로 주변 픽셀로 depth 값을 propagation 하면서 refinement 하게 되는데, 그 propagation 과정에서 guidance feature를 기준으로 사용하게 됩니다. 각 단계가 끝날 때 마다 개선된 depth map D^{k+1}과 propagation 가능한 마스크 M^{k+1}를 같이 업데이트 합니다. 총 K번 반복하고 나서 나오는 최종 depth map은 D_{refined} = D^K와 같이 정의합니다.

3. Experiments

학습 데이터셋은 합성 데이터인 Hypersim과 Virtual Kitti2를, 평가는 real 데이터인 DIODE-Indoor / NYUv2 / ScanNet로 진행하였다고 합니다.

3.1. Sensor depth enhancement

가장 먼저 sensor depth enhancement 성능을 평가하기 위해 노이즈가 포함된 DIODE-Indoor 데이터셋을 사용하여 실험을 진행하였습니다. 근데 이 데이터셋이 정확한 gt를 얻기가 어려워서 개별적인 depth map에 대한 정량적인 평가가 어려웠다고 합니다. 그래서 간접적인 평가 방식으로, refine된 depth map을 사용해서 기존의 relative depth estimation 모델을 fine-tuning한 후에 그 성능에 대해 비교하는 방식으로 진행하였다고 합니다.

사용한 모델은 Depth Anything v1, v2인데 이 두 모델은 모두 원래 DIODE-Indoor로 학습된 적이 없으며, 각 네트워크를 5번씩 fine-tuning해서 평균 성능을 측정하고 있습니다.

비교를 위해서 세 가지 학습 구성을 설정하였는데요,

1. Raw data

→ refinement 없이 원래의 센서 depth map을 그대로 사용

1. Diff only

→ diffusion 단계에서 만든 uncertainty map을 이용해서 신뢰할 수 없는 픽셀을 제거하고, 동일한 diffusion 모델로 빈 영역을 inpaint한 방식

1. Proposed

→ 논문의 최종 전체 파이프라인 (diffusion + deterministic 개선)

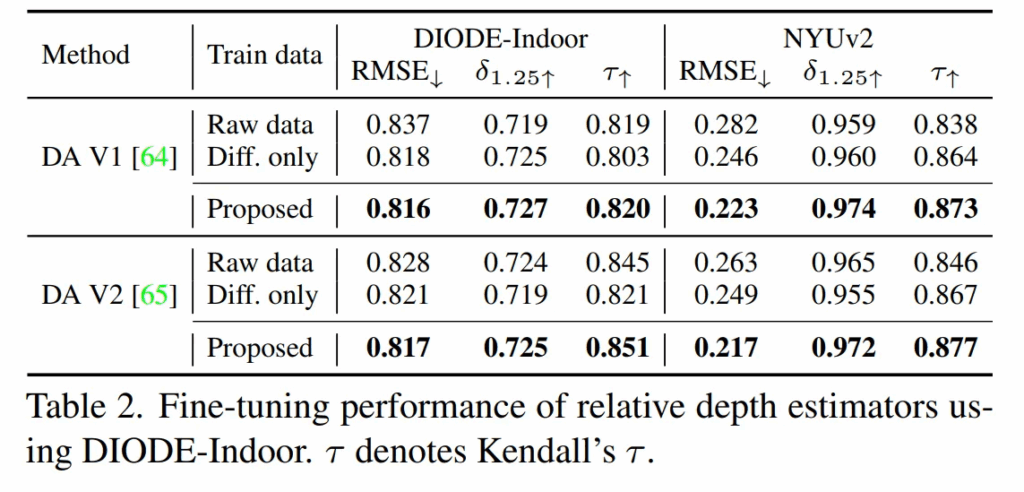
결과는 Tab.2를 보시면 DIODE-Indoor와 NYUv2에 대해서 Proposed 구성이 가장 좋은 성능을 보이고 있는 것을 알 수 있습니다. 특히 Raw data와 Proposed 구성을 비교하였을 때 RMSE와 \tau (정확도를 의미)에서 정량적인 개선이 일어났다고 이야기하고 있습니다. 물론 전 성능 향상이 크지 않다고 느끼긴 합니다만 . . . 저자는 이렇게 이야기하고 있네요.

3.2. Noisy depth completion

해당 실험에서는 센서에서 발생하는 노이즈를 인위적으로 입력에 추가하여 실험을 진행하였다고 합니다. 기존의 depth completion 결과에 노이즈를 추가한 후에 제안한 방법론이 얼마나 아티팩트를 잘 제거할 수 있는지를 평가하였습니다. 기존의 depth completion 방식은 sparse하긴 하지만 노이즈는 사실 없는 depth 값을 사용합니다. 그런데 실제 데이터는 sparse할 수도 있지만 노이즈가 많이 섞여있기 때문에 이러한 환경을 시뮬레이션하여 평가한 것이죠. GT depth에 픽셀을 랜덤으로 선택해서 그 중에 일부를(5, 10, 20%)에 가우시안 노이즈를 추가하였다고 하네요.

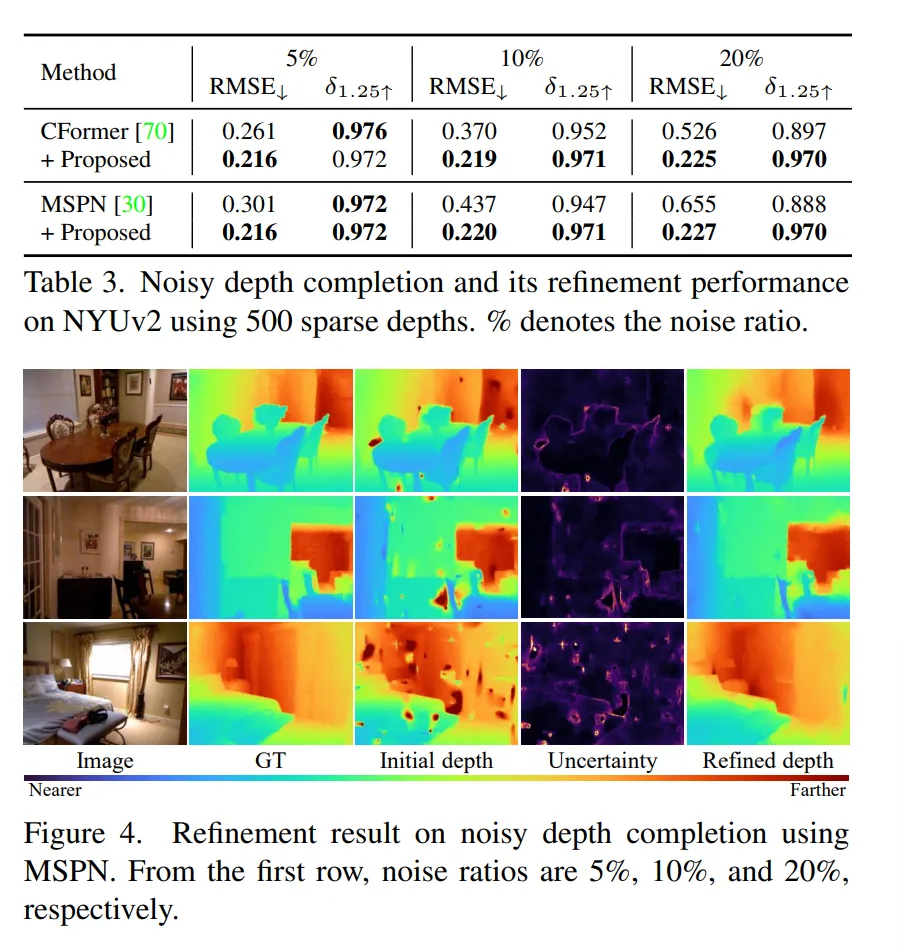
Tab.3을 보면 모든 노이즈 레벨에서 depth 퀄리티를 높일 수 있었고, 합성 데이터만으로 학습했지만 그럼에도 불구하고 실제 노이즈 환경에서도 일반화를 이룰 수 있음을 보여주고 있습니다.

특히 노이즈 비율이 높아질 수록 기존 방법론들은 성능히 급격하게 하락하지만 제안한 방법론을 추가하면 성능 하락이 있긴 하지만 나름의 안정적으로 유지가 되는 것을 알 수 있습니다. Fig.4의 정성적인 결과를 봐도 GT와 유사하게 전체적인 구조와 디테일적인 부분을 표현하고 있습니다.

3.3 Analysis

이제 ablation study인데, 정량적인 실험은 없고 정성적 결과인 Fig.6으로만 보여주고 있습니다.

Number of samples

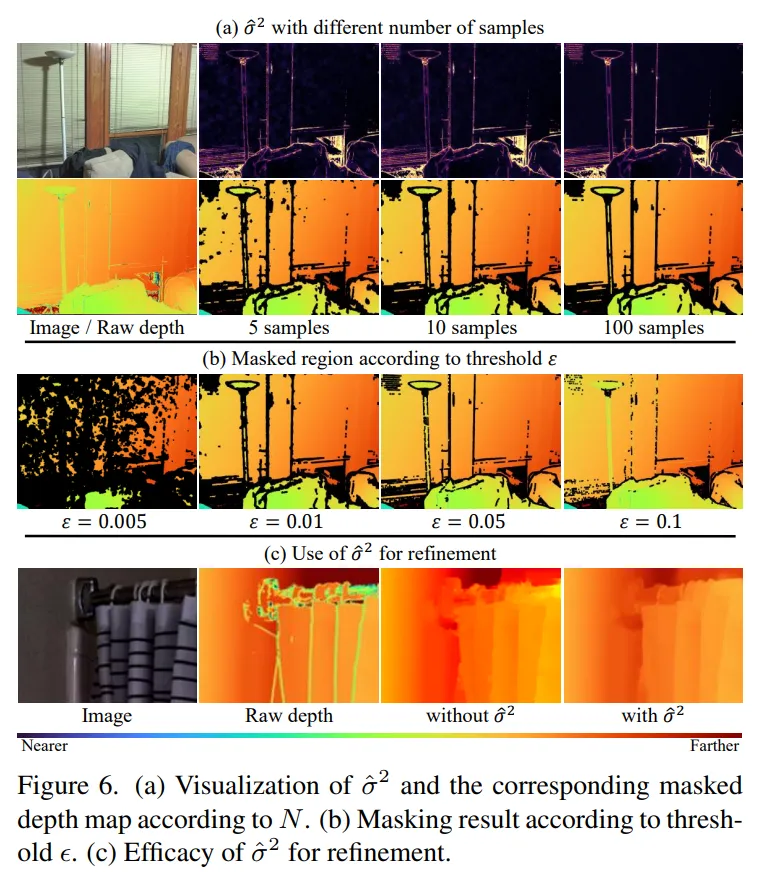
불확실성을 추정하는데 사용하는 \hat{\sigma}^2는 diffusion 모델을 여러번 샘플링하여 계산합니다. Fig.6(a)는 샘플 수 N에 따라 생성된 uncertainty map과 그에 따른 마스킹 결과를 보여주고 있습니다.

결과를 보면, 샘플 수가 10개를 넘어가면 정확도의 향상이 정성적으로 봤을 때 거의 있지 않은데 추론 시간만 증가한다는 것을 확인하였습니다. 그래서 trade-off 관계를 고려하여 기본 샘플 수는 10개로 설정하였다고 합니다.

Threshold

Fig.6(b)는 임계값 \epsilon을 조절하였을 때 마스킹 된 depth map을 확인할 수 있습니다. 실험 결과 \epsilon이 0.01이라는 고정된 임계값만으로도 대부분의 아티팩트를 제거하면서 유효한 depth 값은 또 잘 보존되어 있습니다. 이러한 결과는 복잡한 임계값을 계속 유저가 조절해줄 필요 없이 고정된 임계값으로 안정적인 depth 개선이 가능하다는 것을 보여줍니다.

\hat{\sigma}}^2 for refinement

마지막으로 Fig.6(c)는 refinement 단계에서 \hat{\sigma}^2를 사용할 때와 그렇지 않을 때의 결과를 보여주고 있습니다. \hat{\sigma}^2를 활용했을 때 결과적으로 더 안정적으로 depth refinement가 됨을 정성적으로 알 수 있습니다. 이를 통해 uncertainty 정보를 통해 픽셀마다 refinement 해야 할 대상을 판단하고 조정할 수 있음을 의미하고 있습니다.