이번 리뷰 논문은 Robot의 행동 전략을 LLM으로 사용 했을 때, 발생 가능한 불확실성을 측정하기 위한 논문 입니다. 논문이 어려워 처음에는 oral로 인정 받은 이유를 파악하기 힘들었습니다. 해당 논문은 로봇의 에이전트의 모호성을 해결하기 위한 이론과 이에 대한 증명을 보입니다.. 단, 제약 조건…(e.g. robot observation; 객체 식별, 위치, 객체 간의 기하/의미론적 관계 등)들이 이미 풀어졌다는 전제 하에서의 증명을 수행합니다.
즉, 지능형 로봇의 행동 계획에 따른 불확실성을 해소하기 위한 이론적 근간과 바탕을 제시함으로써, 후속 연구들의 기틀을 마련했다는 점에서 큰 기여도를 받은 것으로 판단됩니다. (제약 조건 안에서 증명을 했으니, 리얼 환경은 후속 연구가…)
Intro
최근 지능형 로봇이 크게 주목 받고 있죠. 특히, LLM은 지능형 로봇의 한 요소로 많이 활용되고 있는 추세입니다. LLM은 로봇 행동 전략에 대한 단계별 계획부터 상식적 추론까지 로봇에 유용한 다양한 추론 능력을 보여주지만, 높은 confidence로 hallucination을 발생 시키는 고질적인 문제점을 가지고 있습니다. 저자는 논문의 첫 글에서부터 “How can we endow our robots with the ability to know when they don’t know?”라는 질문을 던집니다. 해당 문제를 해결하기 위해서 LLM 기반의 planner의 불확실성을 측정하고 aligning을 하기 위한 프레임워크 KNOWNO를 제안합니다.
저자가 고려하는 hallucination에 따른 불확실성을 구체화하고자 합니다. 앞서 언급한 바와 같이 해당 논문은 LLM 기반의 planner의 불확실성을 개선하는 것을 목적으로 합니다. 즉, 사용자의 본래 혹은 의도하지 않아도 발생 가능한 모호한 명령어(e.g. 공간 불확실성, 숫자 불확실성, Winograd schemas*)로 의해 발생하는 문제들이라고 보시면 됩니다.
- Winograd schemas*: 이거, 저거와 같이 의미론적 맥락을 이해해야만 지칭 대상을 알 수 있는 경우
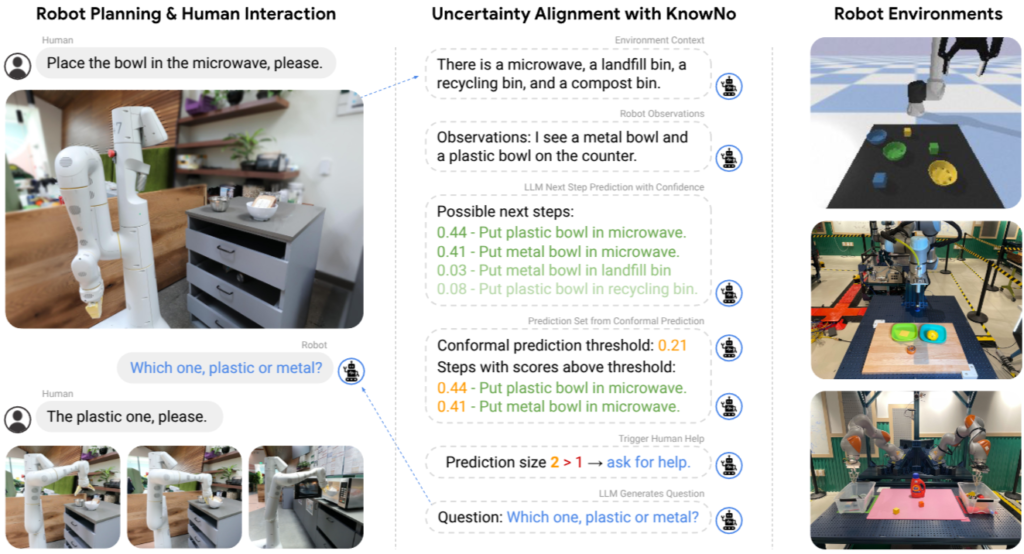
해당 문제는 안전과도 직결되는 치명적인 문제가 될 수 있습니다. 한 가지 예시를 들어보면 위 그림의 왼쪽에 선반 위에 금속 그릇과 플라스틱 그릇이 있습니다. 사용자는 이런 환경에서 “Place the bowl in the microwave, please”라는 명령어를 로봇에게 지시하게 되죠. 해당 경우에서는 그릇이 두 개가 존재하기 때문에 모호합니다. (이런 숫자로 모호환 경우에 오른쪽에 위치한 객체를 우선하여 파지하도록 설계가 되었다고 가정하고) 로봇이 아무런 의심 없이 금속 그릇을 전자레인지이 넣을 경우, 화재와 같은 안전 문제가 발생 할 수 있습니다.
즉, 로봇은 판단이 모호해질 수 있는 스스로 잘 모르는 상황을 알아서 판단하고 다시 되물어 볼 수 있는 능력이 필요하다는 겁니다. 저자는 해당 방법을 구현하기 위해서 2 가지 요구 사항을 정의합니다. 1) calibrated confidence: 과한 confidence를 조절하여 통계적으로 작업 성공 수준을 보장하기 위한 적절한 도움을 요청할 줄 알아야합니다. 2) minimal help: 로봇은 발생 가능한 모호성을 줄여 요청하는 최소한의 도움 요청을 해야 합니다. 저자는 이런 두 요구 조건들을 묶어서 uncertainty alignment라고 통칭합니다.
저자가 제시하는 기여는 다음과 같습니다. LLM based planners의 uncertainty alignment를 수행하기 위해 conformal prediction (CP)* 기반 프레임워크 KNOWNO를 제안합니다. 구체적인 기여 1) 자연어 지시가 주어졌을 때, 사전 학습된 LLM(uncalibrated confidence)을 사용하여 로봇이 다음에 실행 가능한 일련의 행동을 생성합니다. 일련의 행동에 따른 하위 집합을 CP를 사용하여 선택하는 방법을 제시합니다. 하위 집합이 단일 항목인 경우에는 로봇이 실행하도록 진행하며, 여러 항목이 있다면 사용자에게 로봇을 요청하도록 합니다. 2) single-step과 multi-step planning problems 둘 다, calibrated confidence에 대한 이론적 보장을 증명합니다. -> 사용자가 설정한 최대 실패율 ϵ에 따라 도움을 요청하기 때문에 1-ϵ%의 작업 성공률을 보장… 또한 CP로 인해 최소한의 도움을 요청하도록 기능합니다.
3) 가상 환경과 실제 환경에서 KNOWNO를 잠재적 모호성을 가진 다양한 타입의 manipulator 환경에서 평가를 진행합니다. 실험적으로 베이스라인 대비 10-24% 향상된 작업 성공률을 보여줍니다.
- Comformal Prediction (CP) : 기계 학습 모델의 예측에 대한 신뢰도를 평가하고 예측 집합을 생성하여 실제 정답이 포할될 확률을 보장하는 통계적 방법론. -> 불확실성을 정량화하여 예측의 신뢰도를 향상 시키는 것을 목적으로 함.
Method
Overview: Robots that Ask for Help
Language-based planners. Language-based planning에서 언어 모델은 로봇이 수행해야 하는 작업을 단계 별로 계획을 합니다. 각 step y는 variable-length sequences of symbols ( \sigma_1, \sigma_2, \sigma_3... \sigma_k )와 같이 예를 들어 text token으로 구성됩니다. 혹은 조건부 정책 수립 혹은 로봇을 직접 실행하기 위한 코드가 될 수 있습니다. 사전 훈련된 autogressive LLM은 각 단계 y를 예측하고 이 때, 각 토큰의 joint probability는 다음과 같이 conditional probability의 곱으로 표현됩니다. p(y) = \prod_{i=1}^{k} p(\sigma_i \mid \sigma_1, \dots, \sigma_{i-1} 여기서 p(y)는 step y가 발생할 전체 확률을 의미하며, p(\sigma_i \mid \sigma_1, \dots, \sigma_{i-1} [\latex]는 이전 토큰들이 주어졌을 때, [latex] \sigma_i 가 등장할 확률을 의미합니다. 즉, 다음 단계에 대한 uncertainty estimation을 수행하는데에 있어서 p(y)는 k에 따라 예민하게 반응 할 수 밖에 없습니다. 이러한 한계는 저조한 성능으로 이끌어 갈 수 밖에 없습니다.

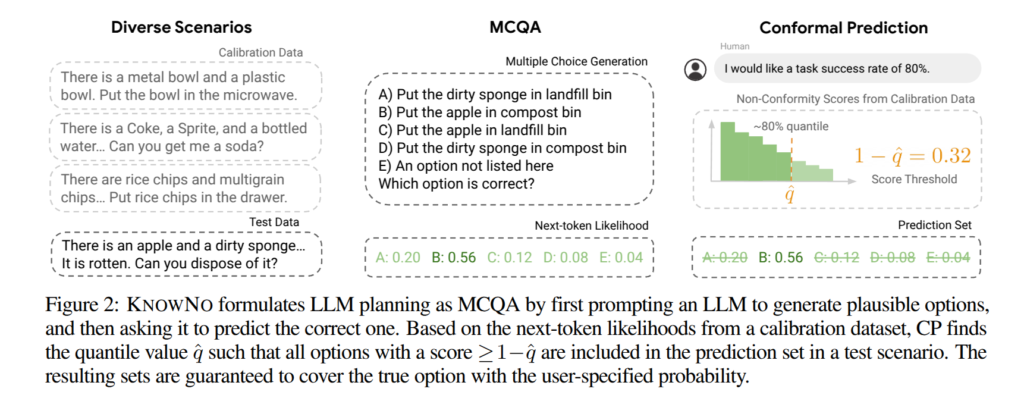
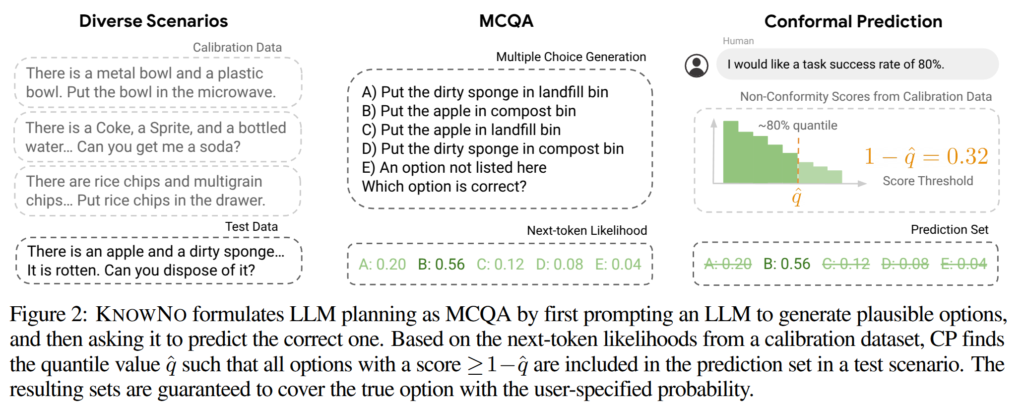
Planning as multiple-choice Q&A. 저자는 길이에 따른 문제점을 간단한 트릭으로 해결합니다. 먼저, fig A1과 같이 candidate next steps (e.g., “Put plastic bowl in microwave”, “Put metal bowl in microwave”)을 포함한 few-shot prompt를 입력하여 생성하도록 합니다. candidate next steps은 서로 semantically different를 가지고 있습니다. 그럼 이는 multiple-choice Q&A (MCQA)로 구성됩니다. 이를 통해 next-token prediction 문제를 가능성이 낮은 단계를 제거하는 방식으로 복잡도를 낮춰 single next-token prediction 문제로 복잡도를 낮춥니다. + (해당 방식은 LLM을 학습하는 데이터 셋 중 MCQA datasets에서의 log-likelihood loss function가 동일한 방법으로 만든거라고 보시면 됩니다.)
저자는 MCQA로부터 normalize score를 추출하여 이를 conformal prediction (CP) 프레임워크를 적용합니다. CP를 통해 candidate next steps에서 MCQA에 대한 후보를 줄이고, 줄어든 후보가 단일 후보라면 해당 step을 선택하고 여러 개라면 유저에게 도움을 요청합니다. 전반적인 과정은 fig 2에서도 확인 가능합니다.
Robots that ask for help. 해당 연구에서는 uncertainty estimation을 위해 CP를 결합한 LLM planning이 효과적으로 환경과 상호작용하면서 도움이 필요한 순간 질의를 던지는 것을 보여줍니다. environment e는 부분적으로 관찰 가능한 Markov decision process (POMDP)로 정의됩니다. 여기서 time t에서의 state s^t 와 user instruction l , robot executes an action a^t 을 따르는 policy \phi 로부터 new state s^{t+1} 를 생성합니다.
- Multiple-choice generation: LLM은 다양한 set of candidate plans labeled 'A', 'B', 'C', 'D', 'E'를 생성합니다. 해당 후보군들은 context x^t 를 베이스로 삼아 프롬프팅이 생성됩니다. 해당 프롬프팅은 다음 내용들을 텍스트로 삼아 생성됩니다. (1) 각 step 마다 로봇의 환경을 관찰한 정보 (e.g. vision-based object detector or an ocracle), (2) the user instruction, (3) few-shot examples of possible plans in other scenarios. 해당 정보를 토대로 기존 context x^t 에 추가되어 augmented context \tilde{x}^t 를 얻습니다.
- Prediction set generation: CP를 활용하여 \tilde{x}^t 로부터 주어진 each prediction y에 대한 LLM's confidence \hat{f}(\tilde{x}^t)_y 에 따라 subset C(\tilde{x}^t)를 선택합니다.
- Human help: 만약 선택된 문항이 단일 문항이 아니라면 사람에게 도움을 요청할 수 있습니다. (혹은 또다른 supervisor agent에게 도움을 요청 할 수 있음) 이를 통해 unambiguous next step에 도달할 수 있습니다.
- Low-level control: 이를 기반으로 plan을 실제 동작을 위한 명령어를 실행합니다.
Goal: uncertainty alignment. 실제 환경에서는 언어 지시가 모호할 수 있습니다. 예를 들어 "place the bowl in the microwave" ~ fig 1과 같은 상황에서 사람은 사전 지식을 토대로 plastic bowl을 넣어야 한다는 것을 알지만 로봇은 이를 판단하기 어렵습니다. 저자는 이러한 uncertainty alignment로 문제를 해결하고자 합니다. 또한, 사람의 도움을 최소화하는 것을 목표로 합니다. 먼저, 해당 상황에 대해서 정리하면 시나리오 ξ := (e, ℓ, g)에 대한 joint distribution D를 고려합니다. 여기서 environment e (POMDP), ℓ은 (potentially ambiguous) language instruction, g는 a goal에 해당합니다. 중요한 점은 D에서부터 지식을 추출하는 것이 아니라 유한한 데이터 셋의 i.i.d. 시나리오로부터 샘플링이 가능하다는 점입니다.
+ 내용이 굉장히 딱딱한데 쉽게 풀어두는 글을 남겨두겠습니다.
- 기존 LLM 기반 planner는 모호함에 대한 불확실성이 어려울 뿐더러, 가변 길이로 인해 이를 정확하게 수치화하기가 어렵다.
- 그래서 이를 해결하기 위해 문제를 단순화하기 위해 다중 문항을 제시하도록 프롬프팅을 수행했다.
- 다중 문항에 대한 답변은 LLM이 학습 방식과 유사하기기 때문에 문항에 따른 score (log-likelihood) 추론이 가능하다. (openai API을 이용하면 5 문항까지는 confidence (score) 값 출력이 가능 합니다)
- 로봇이 관찰된 객체에 대한 정보를 토대로 기존 명령어를 확장하여 생성된 문항을 토대로 CP를 수행해 subset을 선정한다.
- 선정된 subset이 단일이면 그냥 실행, 다중이면 도움을 요청. 유저가 선택하거나 또 다른 agent에게 결정을 맡긴다.
- 결정된 문항에 따라 로봇을 실행한다.
Calibrating LLM Confidence with Conformal Prediction
Background: Conformal Prediction. 해당 부분은 간단하게 설명하겠습니다. CP의 역할은 LLM의 불확실성을 측정하고 보정하여 로봇이 작업을 성공적으로 완료할 확률을 보장한데에 있습니다. 먼저, 입력 \tilde{x} 와 실제 레이블 y로 구성된 일반적인 MCQA (Multiple-Choice Question Answering) 설정을 고려합니다. unknown distribution D에서 i.i.d.(independent and identically distributed, 독립 동일 분포)로 추출된 쌍 (x_i, y_i) 의 calibration set Z = {z_i = (\tilde{x}_i, y_i)}_{i=1}^{N}이 있다고 가정합니다. 여기서 Z는 X \times Y 의 부분집합입니다. unknown true label y_{test} 를 가진 새로운 i.i.d. 샘플 z_{test} = (\tilde{x}_{test}, y_{test})가 주어졌을 때, CP는 높은 확률로 y_{test} 를 포함하는 예측 집합 C(\tilde{x}_{test}) \subseteq Y 를 생성합니다. 이에 따른 확률은 다음과 같이 정의 할 수 있습니다.
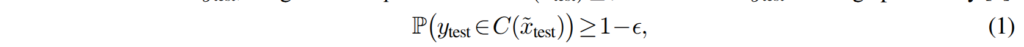
여기서 1 - \epsilon 은 사용자가 지정하는 값 (원하는 작업 성공 수준)이며, C()의 크기에 영향을 미치게 됩니다.
C(\tilde{x}_{test})를 생성하기 위해 CP는 먼저 LLM의 confidence \hat{f} 를 사용하여 calibration set에 대한 nonconformity score set {\kappa_i = 1 - \hat{f}(\tilde{x}_i)_{y_i}}_{i=1}^N을 평가합니다. 점수가 높을수록 calibration set의 각 데이터가 \hat{f} 훈련에 사용된 데이터와 덜 일치함을 의미합니다. CP는 \hat{q} 를 \kappa_1, …, \kappa_N 의 \frac{\lceil (N+1)(1-\epsilon) \rceil}{N} empirical quantile로 정의하여 calibration을 수행합니다. 최종적으로 CP는 아래 수식을 통해 subset을 선별하게 됩니다.
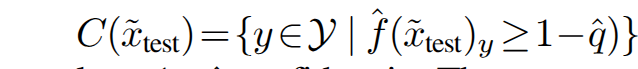
+ 수식이 많아 복잡한데... 쉽게 풀면 1 - \epsilon 을 보장하기 위한 영역을 선별하기 위해 생성한 표본 데이터 셋 ~ calibration set으로부터 confidence를 생성하고 이에 대한 empirical quantile을 선정하여 이를 threshold로 사용합니다.
+ 더 쉽게 풀면 calibration data => 관찰된 환경*에서 가능한 잠재적 모호한 명령어를 뽑아둔 것 => 부분 집합을 활용해 확률 분포를 생성하고 이에 대한 분위를 지정한 성공률 수준을 활용해 사분위를 선정하여 후보 셋을 거르는 작업이라고 보시면 됩니다.
++ 관찰된 환경*: 객체 인식, 위치 등 환경 정보과 같이 로봇이 임무를 수행하기 위해 알고 있어야 하는 환경 정보입니다. 해당 논문에서는 객체 인식, 위치 등 환경 정보를 알고 있다는 가정 하에서 진행됩니다.
Dataset-conditional guarantee. 수식 1은 calibration set Z와 z_test를 모두 고려한 것으로 새로운 z_test마다 새로운 calibration set이 요구된다는 이야기입니다. 이를 해결하기 위해 저자는 dataset-conditional guarantee를 적용합니다. 이는 새로운 test data에 재보정 없이 적용 가능하다는 의미 입니다.
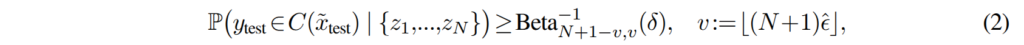
여기서 Beta^{-1}_{N+1-v,v}(\delta) 는 파라미터 N+1-v 와 v를 가지는 Beta 분포의 역 누적 분포 함수(CDF)의 \delta 분위수 수준을 나타냅니다. \hat{\epsilon}는 calibration에 사용되는 threshold입니다. 실제 실험에서는 적당한 크기의 calibration dataset (N = 400)과 \delta = 0.01을 사용하고, 원하는 1 - \epsilon 커버리지를 달성하기 위해 \hat{\epsilon} 을 조정합니다. 이를 통해 calibration set 샘플링에 대해 1 - \delta = 0.99의 확률로 원하는 커버리지를 얻을 수 있습니다.
+ 여긴 표본 집합만을 이용하여 커버리지 보장을 하기 위한 이야기라고 보시면 됩니다.
+ 그렇기에 생성한 calibration data의 분포를 활용하기 위한 내용이며, 역 누적 분포 함수 CDF는 확률을 입력하면 그에 따른 분위를 출력하는 함수이며, Beta 분포는 a, b로 구성하여 분포를 그릴 수 있는 분포입니다. a는 1에 가까운 성공 횟수 (N+1-v), 0에 가까운 실패 횟수(v)로 보시면 됩니다.
+ 쉽게 풀면 매번 새롭게 test에 맞추는 것은 불가능하기 때문에 표본 데이터를 이용하여 얻은 임계값을 사용하자고 이해하시면 됩니다.
Minimal prediction set size. 해당 파트에서는 CP가 어떻게 최소의 평균 집합 크기를 달성하는지에 대한 이론적 근거와 그 중요성을 설명합니다. 만약 \hat{f}(\tilde{x})_y을 따르는 true conditional probabilities에 대한 모델링을 한다면 다음과 같이 정의됩니다.
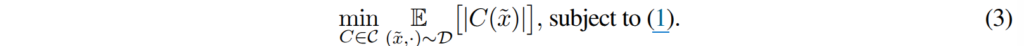
여기서 C는 가능한 모든 예측 방식(prediction scheme)의 집합, \mathbb{E}_{(\tilde{x}, \cdot) \sim D}[|C(\tilde{x})|]는 데이터 분포 D에 따라 입력 ~x에 대한 예측 집합 C(~x)의 크기의 기댓값. 즉, 평균적인 예측 집합의 크기를 의미합니다. subject to (1)은 수식 1에서 제시된 제약 조건을 만족해야 한다는 의미로 실제 정답을 포함해야하는 확률이 최소한 1-e이여야 한다는 의미를 가집니다.
+ 말이 복잡한데... 모델의 예측 값을 토대로 연산이 수행되기 때문에 최소한의 예측 집합이 보장된다는 이야기입니다....
Single-Step Uncertainty Alignment
해당 섹션에서는 CP를 사용하여 사용자가 지정한 1-e에 대한 LLM 기반 planner의 uncertainty alignment를 달성하는 방법을 보여줍니다. 여기서는 single-step을 사용하기 때문에 time step t를 생략합니다.
Data collection. 먼저 distribution D에서 N개의 독립적으로 동일하게 분포된 시나리오를 수집하고, robot observation and instruction을 요약한 context x를 얻습니다. 그 다음 MCQA을 적용해 candidate plans을 생성하고, 각 augment context ˜x (즉, 계획과 결합된 컨텍스트)에 올바른 레이블을 붙입니다. 이를 통해 augment context와 올바른 레이블 쌍으로 이루어진 calibration set Z = {zi = (\tilde{x}_i, y_i)}_{i=1}^N 을 얻습니다.
Calibration. 그 다음 먼저 1-e를 달성하기 하기 위해서 \hat{\epsilon} 를 조정하고 그 다음 quantile \hat{q} 를 얻습니다. 주어진 새로운 x_test로부터 1-e 확률로 y_test를 포함하는 calibration set C(~x_test)구성 할 수 있습니다.
Triggering help. 만약에 단독이면 그대로 실행하고, 아니라면 사람에게 후보 셋 중에서 선택하도록 도움을 요청합니다.
Multi-Step Uncertainty Alignment
이전 까지는 single-step이라는 전제 하에서 증명을 했기 때문에 i.i.d.가 성립했습니다. 하지만 연속적인 시간에 따라 미래 스텝에 영향을 주기 때문에 i.i.d가 깨지게 됩니다. 그렇기에 저자는 각 스텝들을 독립적인 정보로 보지 않고 시퀀스 정보로 받아 들이는 방법을 제시합니다.
Sequence-level calibration. single-step과 유사하게 time t \in T 에 따른 augment \bar{x} = (\tilde{x}^0, \tilde{x}^1, …, \tilde{x}^{T-1}) 와 true label \bar{y} = ( y^0, ..., y^{T-1} ) 를 생성하여 \bar{z}를 생성합니다. 그 다음, 아래 수식과 같이

타임스탬프 내에서 가장 낮은 스코어를 가진 스탭의 스코어를 사용합니다. 그리고 single과 동일하게 아래 수식을 이용하여 새로운 \hat{q} 와 prediction set을 구합니다.
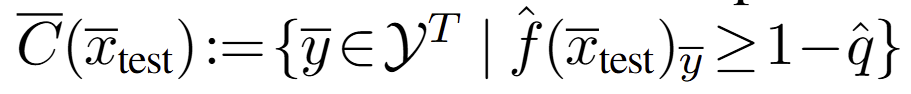
Causal reconstruction of C(x) at test time. single-step과 동일하게 test 중에는 z_test를 구하는 것이 어렵습니다. 가장 어려운 이유는 미래 정보를 결정하는 것이 매우 어렵다는 점입니다. 그렇기에 과거에 결정된 정보와 현재 시점의 후보 군들 이용해 casual manner (인과적인 방법; 시간 흐름에 따른 방식)을 제안 합니다. 각 step 간의 결정은 아래와 같이 각 스텝의 prediction set 간의 곱집합으로 표현 가능합니다.
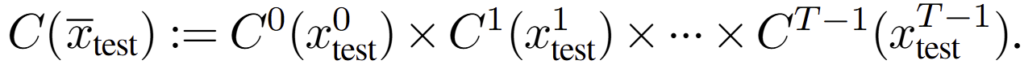
저자가 주장하길 아래 수식과 같이 lower bound on the sequence-level coverage를 얻을 수 있으며,
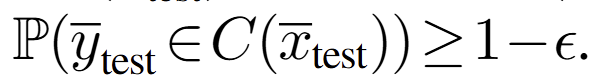
이에 따라 아래 수식과 같이 sequence-level calibration과 casual manner로 구한 prediction set은 동치라고 볼 수 있다고 합니다.
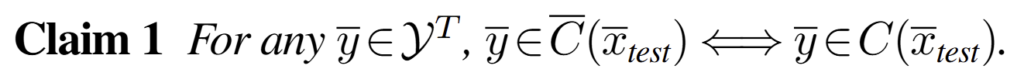
이후 단계는 single-step과 동일합니다.
Experiment
해당 실험에서는 다양한 언어 지시 작업 및 환경에서 프레임워크를 평가하고, 사용자 지정 작업 완료 비율을 달성하면서 사용자 도움을 최소화하는 데 효과적임을 보이고자 합니다. 해당 실험에서는 LLM운 PaLM-2L을 메인으로 사용합니다.
Scenario Distribution and Calibration Dataset. 해당 실험은 i.i.d를 보장 할 수 있는 calibration data를 생성해야만 합니다. 그렇기에 로봇이 관찰하는 환경 정보를 i.i.d를 따르는 표본 집합을 만들 수 있다는 가정을 전제합니다. 해당 실험에서의 구성은 논문의 Section A7에서 확인 가능합니다. 각 calibration data는 해당 분포에서 무작위 샘플링을 통해 생성됩니다. Multi-step setting에서는 calibration data 를 라벨링하는 데 약 4시간 소요되며, single-step setting에서는 1.5시간이 소요됩니다.
Baseline. Simple Set: calibration data로 q를 재보정 없이 KnowNo와 동일한 구성. Ensemble Set: 20번 예측을 반복하고 등장 빈도를 이용하여 결정. Prompt Set: LLM이 prediction set을 직접 예측하도록 함. Binary: score를 이진으로 분류. No Help: 사람의 도움 없음
Simulation: Tabletop Rearrangement. 세 종류의 모호한 표현에 대한 작업 완료 비율을 평가 (1) Attribute: e.g. 그릇->국 통* (2) Numeric: e.g. 저기에 있는 책 몇 개만 옮겨 줄래?. 수의 모호성. (3) Spatial: e.g. 그릇 옆에 사과를 놓아 줄래? -> 그릇의 상단/하단/오른쪽/왼쪽 등 위치의 모호성
* 이해를 위해... 논문과 다른 예시를 사용함
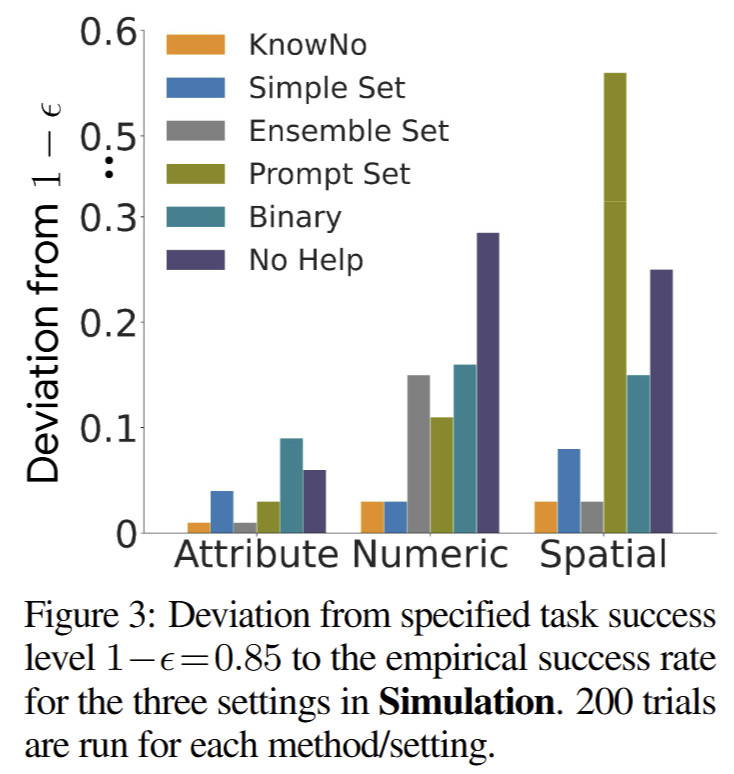
해당 실험에서는 1-e는 0.85를 설정했으며, fig 3에 따르면 KnowNo가 3 종류의 모호한 표현에서 가장 작은 편차를 보임.
+ 해당 실험을 통해 몇 가지 재밌는 결과를 볼 수 있음. prompt set이 LLM에게 결정을 맞기는 세팅임. 의미론적인 경향을 보이는 Attribute에서는 KnowNo와 동등한 편차를 보이나, 공간적인 특색을 보이는 상황에서는 가장 높은 편차를 보임.
+ 또 다른 특징적인 부분은 Simple set이 전체 베이스라인에서 차지하는 평균 순위가 2위를 차지한다는 점으로 보임. MCQA와 이에 따른 confidence에 대한 임계값 처리를 해주는 기법만으로도 다른 베이스 보다 좋은 결과를 보여주었다는 의미로 추후에 confidence를 활용하는 방향에 대해서 진지하게 생각할 필요가 있다고 보임
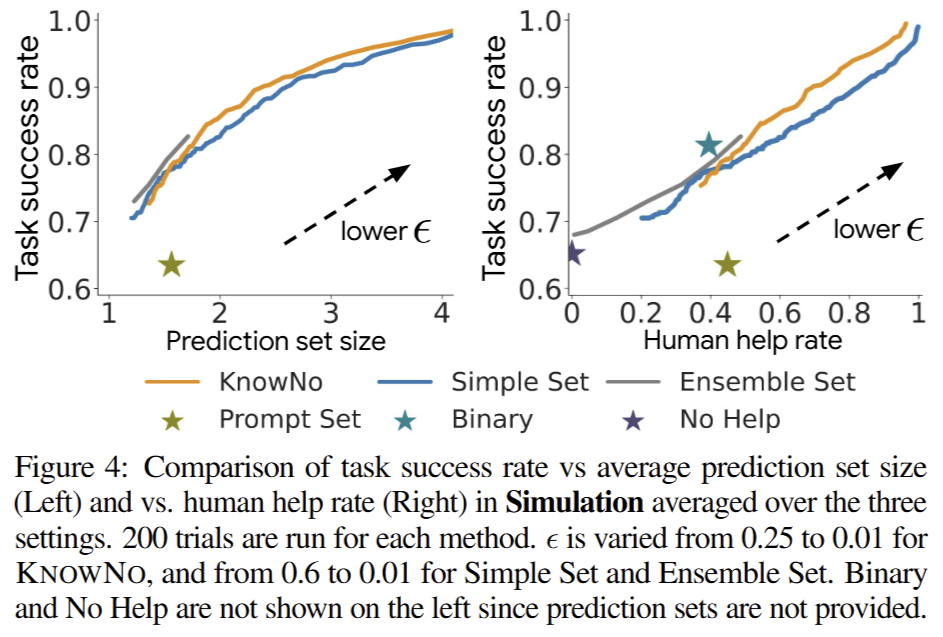
Fig 4에서는 목표 에러율 e와 prediction set size, Human help rate에 대한 관계성을 보이는 실험 결과 입니다. 저자가 목표한 바와 같이 목표 에러율을 거의 보장하는 결과 (KnowNo:0.25-0.01, SimpleSet:0.6-0.01)를 보여주고 있지만 낮아지면서 human help rate도 동일하 증가하는 경향을 보이고 있습니다.
Hardware: Multi-Step Tabletop Rearrangement
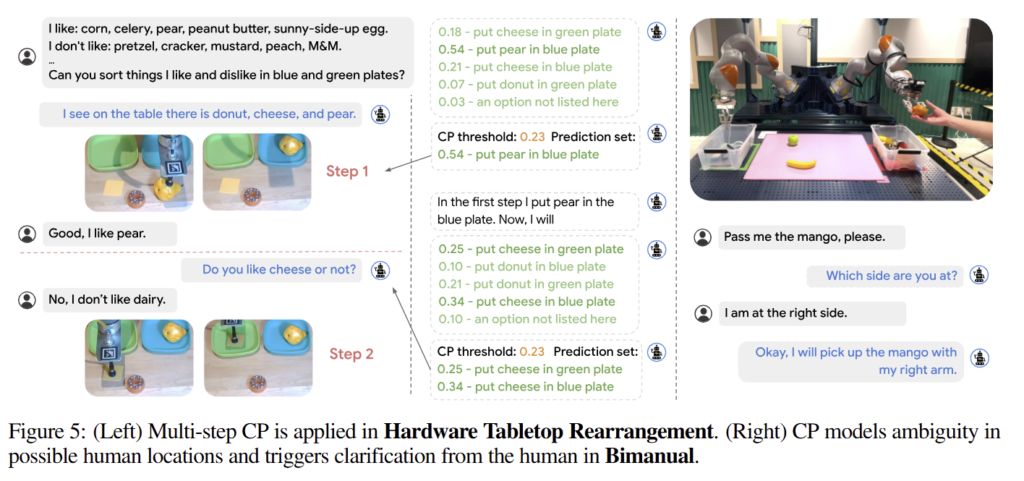
fig 5는 multi-step CP를 실제 Tabletop Rearrangement에 적용한 결과임. 중간 하단을 보면 CP 임계를 초과하는 문항이 두개가 등장하여 유저에게 도움을 요청하는 것을 볼 수 있습니다.
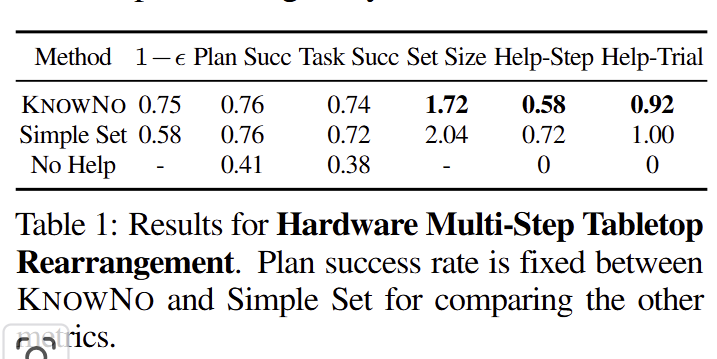
정량적인 결과는 tab 1에서 확인 가능함. KnowNo가 가장 좋은 결과를 보임. 또한 tab 1의 1-e와 Plan Succ의 편차가 가장 적은 결과를 통해 목표 에러율에 대한 커버리지를 보장하는 결과를 보여줌
Hardware: Mobile Manipulator in a Kitchen
주방 환경에서의 Winograd Schema과 다양한 모호성에 대한 평가를 진행함. 실험 결과는 tab 2에서 확인 가능
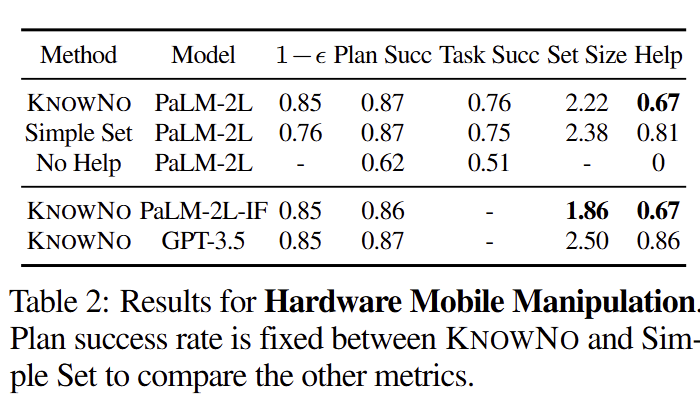
KnowNo가 다른 기법에 비해 average prediction set size과 Human help rate가 낮은 결과를 보여
+ Tab 2의 하단 2열은 다른 LLM(더 좋은)을 사용했을 때의 결과, PaLM-2L-IF를 사용했을 때, 전반적으로 개선된 결과를 보임. GPT-3.5은 문항 중 D,E에 편향되어 선택하는 경향을 보여 기대보다 낮은 결과를 보였다고 함.
++ 문항에 따른 LLM의 confidence를 이용한 방법은 LLM의 특성을 크게 고려해야 할 것으로 판단
논문을 이해해보니... 범용성이 드러나는 논문으로 보임.... 허나... 시나리오 맞는 calibration data 구축이 어려워 보임... 이를 보완 할 수 있는 기법이 굉장히 필요해 보이는 기