안녕하세요 본 리뷰는 일반적인 딥러닝 모델(Deterministic model)에서 불확실성을 추론하는 방법의 베이스라인을 제시하는 논문을 소개하려고 합니다. 앞서서 Bayesian learning의 장점은 불확실성을 이론적으로 정의하여 추정할 수 있는 것이라고 말씀드렸는데요, 딥러닝에서도 불확실성의 추론을 가능하게 하기 위한 기준을 제시한 논문입니다. 그럼 리뷰를 시작하겠습니다.
용어
# 불확실성: 기계학습에서 불확실성은 주로 2가지로 나뉩니다: epistemic uncertainty, aleatoric uncertainty; epistemic(aka systematic) uncertainty란 정보의 부족으로 발생하는 불확실성을 의미하여 일반적으로 모델의 불확실성 상태를 의미합니다. 반면 aleatoric(aka statistical) uncertainty는 randomness로 인한 불확실성으로 시스템이나 환경에 내재된 무작위성에 의한 고유한 불확실성을 의미합니다. 일반적으로 epistemic uncertainty는 데이터의 추가 등으로 reducible하다고 여겨지며, aleatoric uncertainty는 내재된 불확실성으로 irreducible 하다고 여겨집니다.
소개
모두가 아시다시피 불확실성의 추정은 인공지능에서 중요한 요소입니다. 메타인지를 통해 앎을 정의한 소크라테스의 격언처럼 기계가 인지나 추론을 “알고 있는 지식”을 기반으로 잘 수행하고 있다면, 모르는 것은 모른다고 할 수 있어야 하기 때문이죠.
위와 같이, 추상적인 필요를 제외하고도 불확실성의 정량화는 인공지능의 산업적 활용에서도 필수적입니다. 잘못된 예측을 낮은 불확실성으로 예측해야, 해당 예측을 통한 추론/액션을 수행하지 않을 수 있기 때문입니다. 예를 들어 자율주행을 위한 보행자 인식 알고리즘이 기체등을 사람으로 잘못 인식할 때 낮은 불확실성으로 예측해야, 해당 예측을 주행 추론에 반영하지 않을 수 있고, 불필요한 차선 변동 등을 줄여 효율적인 경로 추론을 수행할 수 있습니다.
본 논문은 인공지능의 중요한 속성인 불확실성을 정의하는 베이스 라인을 제시합니다. 물론, 불확실성을 정의하는 전통적인 방법(베이지안 러닝 등)은 이미 존재합니다. 그러나 해당 방법들은 연산량이 높다는 문제점이 있습니다. 대표적으로 앙상블 기반의 베이지안 러닝은 특정 분포를 일정 이상 샘플링 하면 실제 분포를 모사할 수 있다는 대수의 법칙을 기반으로 설계되어 모델의 불확실성을 확률적으로 정의할 수 있지만, 여러 모델을 학습해야 하기에 메모리와 연산량이 일반적인 딥러닝 모델 대비 높습니다. 이에 대한 대안으로 single-forward pass models을 활용한 uncertainty 추론 방법(즉, 추론 과정에서 uncertiainty를 추론하는 방법)이 제시되기도 했습니다[1][2]. 본 논문은 single-forward pass models 방법을 기반으로, 전통적인 방법론 대비 낮은 연산량으로 더욱 정확한 불확실성을 정의하는 베이스라인인 Deep Deterministic Uncertainty (DDU)를 제시합니다. 이는 기존 방법론 대비 직관적이면서도, 불확실성을 활용해 수행할 수 있는 OoD(Out-of-distribution) detection, active learning 등에서 높은 성능을 보임으로서 우수성을 증명했습니다.
관련 기존 연구
본 논문의 앞선 연구로는 DUQ[1], SNGP[2]가 있습니다. 두 방법 모두 모델을 분포로 정의하여 불확실성을 추론하는 전통적인 방법이 내재하는 고연산량이라는 문제를 다루기 위해 single-forward pass, 즉, 추론과정에서 특정 기법을 적용해 불확실성을 근사화하는 방법들 입니다. 즉 결정론적 모델인 일반적인 딥러닝에서 특정 근사 과정을 제안하여 불확실성을 정량화하는 방법을 제시한 논문들이죠.
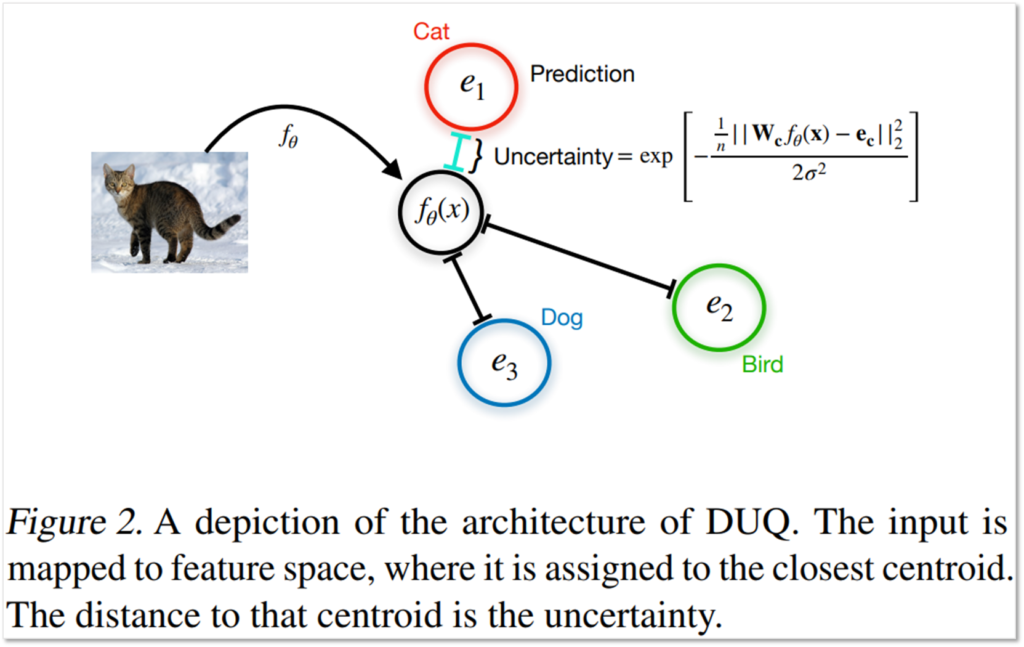
간단하게 소개하자면, DUQ(deterministic uncertainty quantification)는 모델을 설계할 때 부터 임베딩 공간상의 거리가 uncertainty를 산출할 수 있도록 설계하는 방법입니다. 모델을 학습하고 나면, 각 카테고리의 센터(e)를 정의한 다음 x의 임베딩 위치인 f(x)와 카테고리 센터(e)간의 거리를 통해 불확실성을 산출하게 됩니다.
다음으로 SNGP(Spectral-normalized Neural Gaussian Process)는 Spectral-normalization이라는 정규화 기법을 정의합니다. 본 논문은 해당 정규화를 적용하고, Gaussian process를 통해 예측과정에서 불확실성을 산출하였을 때, 기존의 Gaussian process 기반의 불확실성 추청보다 효과적임을 보이는 논문입니다. 아래는 SNGP의 알고리즘이며, 학습과정에 제안된 Spectral Normalization을 수행하고 Gaussian process를 통해 예측을 수행함을 확인할 수 있습니다.

본 논문이 제시하는 DDU(Deep Deterministic Uncertainty)역시 위의 두 기법처럼 예측 모델을 분포로 설정하여 불확실성을 계산하는 것이 아니라, 근사를 통해 불확실성을 직접 예측하는 방법입니다. 하지만, 아래의 수도 코드에서 확인할 수 있듯이 기존 연구에서 구분하지 못했던 epistemic uncertainty와 aleatoric uncertainty를 나누어서 산출 할 수 있어 기존 방법론 대비 더욱 직관적이고 해석 가능성을 높인 베이스라인이라 할 수 있습니다.

본문
논문이 제안한 베이스라인은 SNGP와 DUQ를 계승한 계산효율적 불확실성 추정 방법임에도, 정통적인 불확실성 추정 방법처럼 aleatoric uncertainty와 epistemic uncertainty를 계별적으로 산출하도록 합니다. 또한 SNGP에서 제안된 정규화 방법을 통해 개선된 feature-space를 모델링하는 등 추가적인 테크닉을 적용하여 기존 방법론 대비 불확실성 산출의 개선된 효과를 실험으로 보입니다. 이어서 제안된 베이스라인인 DDU에 대해 특징을 기반으로 자세하게 알아보겠습니다.
- 특징1: 두 가지 불확실성을 구분할 수 있는 프레임워크
본 논문이 제시하는 베이스라인의 가장 큰 장점 중 하나는 근사 방법임에도 불구하고 aleatoric uncertainty와 epistemic uncertainty를 구분할 수 있다는 것입니다. 해당 구분이 필수적인 이유는 두 불확실성의 성격이 완전히 다르기 때문입니다. aleatoric uncertainty는 시스템 내재적인 불확실성으로 동일 시스템이라는 도메인 안(즉, in-distribution)에서만 유효한 값을 산출 할 수 있습니다. 한편 epistemic uncertainty는 정보량 부족을 의미하여 out-of-distribution 등, 학습하지 않은 데이터에 대한 불확실성을 산출하는데 효과적입니다. 우리가 불확실성을 주로 활용하는 테스크인 *OoD(Out-of-distribution) detection, active learning 역시 두 타입의 불확실성에 대한 구분이 중요합니다.
*OoD detection은 모델의 추론에서 학습되지 않은 입력을 검출할 수 있게 하여, 틀린 예측을 사전에 방지하는 안전한 인공지능 서비스 설계에 필수적이며, Active Learning은 인공지능 모델을 업데이트 할 때, 학습 데이터 셋을 설계할 때 필수적입니다. Active Learning은 일반적으로 낮은 aleatoric uncertainty를 갖으며 높은 epistemic uncertainty를 갖는 데이터를 고가치 데이터로 정의하며, OoD Detection은 높은 aleatoric uncertainty(즉 분포 내 데이터의 노이즈 등으로 인한 불확실성)을 epistemic uncetainty(분포외 데이터, 학습하지 않음으로 유래된 불확실성)와 구분하는 것이 메인 테스크 입니다.
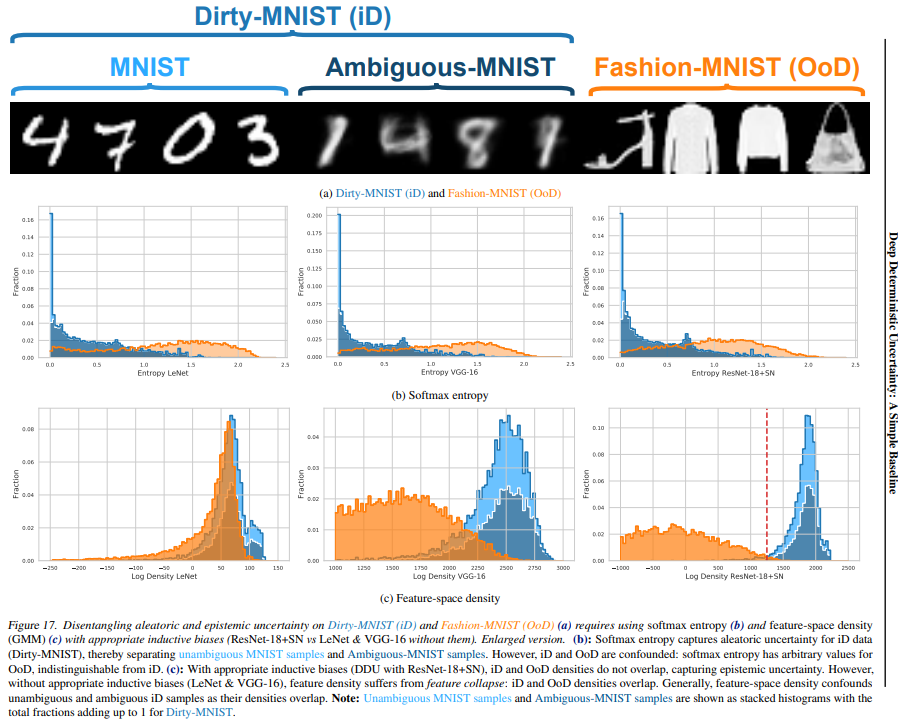
위의 메인 이미지는 MNIST 데이터 셋을 기준(unambiguous domain)으로 in-distribution 내의 모호성을 포함한 도메인인 Dirty-MNIST(ambiguous domain)와 Fashion-MNIST(out-of-domain)을 aleatoric uncertainty와 epistemic uncertainty를 통해 구분할 수 있음을 시사합니다.
위 그림의 (b)는 Softmax 출력을 통한 불확실성 추정 결과입니다. 결과를 통해 in-distribution의 MNIST와 Dirty-MNIST 는 구분이 되지만, Dirty-MNIST와 Fashion-MNIST 분포간의 구분은 명확하지 않음을 통해, out-of-distribution에서 softmax entropy를 통한 불확실성 산출이 효과적이지 않음을 알 수 있습니다.
한편 (c)의 feature-space 의 밀집도를 기반으로 불확실성 기반의 구분을 한 결과, in-distribution(MNIST&Dirty-MNIST)와 out-of-distribution(Fashion-MNIST)의 구분이 확연하게 구별됨을 알 수 있습니다.
정리하면, Softmax entropy(b)는 in-distribution 내의 불확실성을 구분하는데 효과적이므로 aleatoric uncertainty 산출에 활용할 수 있으며 feature-space의 밀집도를 기반으로 산출하는 불확실성(c)은 OoD 구분에 효과적이므로 epistemic uncertainty 산출에 효과적임을 알 수 있습니다. 이러한 인사이트를 기반으로 논문은 DDU 알고리즘을 설계하였으며 “관련 기존 연구의 [DDU(본 연구) 의 전체 알고리즘]”에서 두 불확실성 산출 방식을 어떻게 활용하는지에 대한 전체 프레임워크를 확인할 수 있습니다.
- 특징2: 기존 연구의 feature normalization 방법 등으로 aleatoric uncertainty 산출 정확도 개선
본 논문은 앞서서 소개한 것처럼 두 가지 불확실성 산출 방법을 통해 aleatoric uncertainty와 epistemic uncertainty를 구별하여 산출합니다. 특히 spectral normalisation을 적용하여 feature space를 모델링하고, 개선된 feature space를 통해 Out-of-distribution 데이터와 in-distribution 데이터의 표현공간 상의 충돌 없이 거리를 모델링할 수 있습니다.
- uncertainty 산출 방법 상세
epistemic uncertainty와 aleatoric uncertainty의 상세한 산출 방법은 다음과 같습니다. 먼저 OoD의 구분에 활용되는 epistemic uncertainty는 feature-space상의 거리 정보를 이용하여 *GDA(Gaussian Discriminant Analysis)를 수행으로 불확실성을 추정합니다. spectral-normalization을 통해 collapse 없이(즉, OoD와 in-distribution을 잘 구분한다는 의미) uncertainty를 잘 반영한다는 가정하에 클래스 별로 가우시안 분포를 모델링합니다.
* GDA는 기 학습된 데이터로 계산되는 클래스 mean과 covariance를 이용해 클래스 분류기를 가우시안 분포로 모델링하여, 주어진 입력 데이터가 특정 클래스에 속할 확률을 추정하는 방법입니다. 이때 normalization을 적용하지 않으면 out-of-distribution에 대응력이 낮아져 해당 데이터가 in-distribution 영역으로 임베딩 되는 collapse 현상이 발생할 수 있습니다.
다음으로 aleatoric uncertainty는 단순히 모델의 softmax output에 대한 entropy 산출 식으로 정의됩니다. 이때, softmax 출력은 Deep learning 모델 출력의 overconfidence 현상을 완화하기 위한 calibration 기법인 temperature scaling이 적용됩니다. 이는 스케일링 파라미터 T로 모델 예측 출력값인 logits를 나누는 단순한 후처리 방법입니다.
실험
uncertainty는 정답값을 사람이 생성할 수 없으므로 직접적인 비교가 어렵습니다. 따라서 본 논문은 uncertainty를 활용하는 Active Learning과 OoD(Out-of-distribution) Detection을 수행하여 비교 방법론 대비 효과적이였음을 보였습니다. 또한 Semantic segmentation task에서 uncertainty를 시각화하므로써 제안한 방법론이 컴퓨터 비전 분야에서도 *동일한 메커니즘으로 활용될 수 있음을 보였습니다.
* 동일한 메커니즘이란: 시스템 내재적인 불확실성(aleatoric uncertainty)이 컴퓨터 비전에서는 보통 카메라 촬영 오차등으로 인한 엣지 라인에 대한 불확실성으로 해석되는 한편, 정보량에 의거한 불확실성(epistemic uncertainty)은 물체의 내부 영역 등에 대한 예측 불확실성으로 해석됩니다. 이처럼 각 불확실성이 비전 테스크의 예측에서 어떻게 발현하는지에 대한 메커니즘을 의미합니다.
- Active Learning
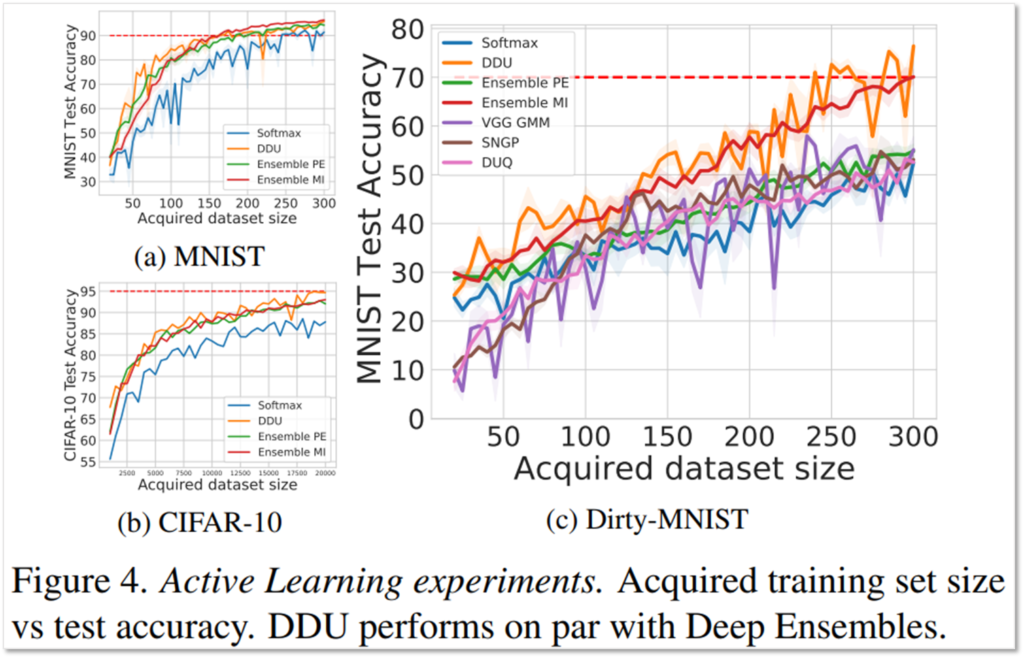
Active Learning은 후보 데이터셋에서 학습에 사용할 데이터를 선택하여, 적은 양의 데이터로 빠르게 모델의 성능을 개선하는 테스크로, epistemic uncertainty가 높은 데이터를 선택하는것이 효과적이며, 소량의 데이터를 선별해야 하기에 aleatoric uncertainty는 낮은, 즉 시스템 렌덤 노이즈가 적게 포함된 고품질의 데이터를 선택하는 것이 좋습니다.
논문은 in-distribution 내의 데이터 불확실성과 out-of-distribution의 데이터 정보량 불확실성이 Active Learning에 어떻게 동작하는지 보이기 위해 3가지 세팅해서 실험을 진행하였습니다:
- (a) clean MNIST 로 구성된 후보 데이터군 (in-distribution with low uncertainty)
- (b) clean CIFAR-10 로 구성된 후보 데이터군 (out-of-distribution)
- (c) clean CIFAR-10+ Dirty-MNIST로 구성된 후보 데이터군 (MNIST:Ambiguous-MNIST=1:60 비율) (mixed with out-of-distribution & in-distrubution data with high uncertainty, 현실과 가장 가까운 세팅)
실험 결과 제안하는 방법(DDU)이 실제 세계(real-world)의 세팅인 (c)에서 가장 효과적임을 확인할 수 있습니다. in-distribution만 존제하는 세팅에서는 기존 방법 역시 효과적이였지만, out-of-distribution으로 구성된 (b)세팅에서는 제안된 방법인 DDU가 가장 효과적임을 확인할 수 있었습니다.
- Out-of-distribution Detection
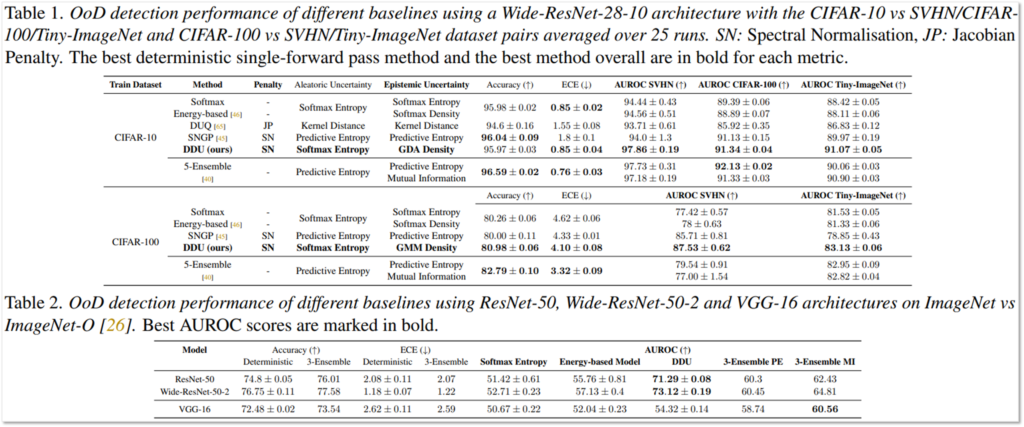
Out-of-distribution(OoD) Detection 테스크는 in-distrubution간의 uncertainty인 랜덤 노이즈와 out-of-distribution에서 발생하는 지식 부족으로 인한 uncertainty를 구분하는것이 중요한 테스크입니다. 이는 aleatoric uncertainty가 아닌 epistemic uncertainty를 통해 도메인을 구분할 때 수행할 수 있으며, 비교 방법론(softmax entropy, energy-based model, ensemble) 대비 일반적으로 검출 효과가 높음을 확인할 수 있습니다.
- Computer vision에서의 활용 가능성: Semantic Segmentation에 대한 적용
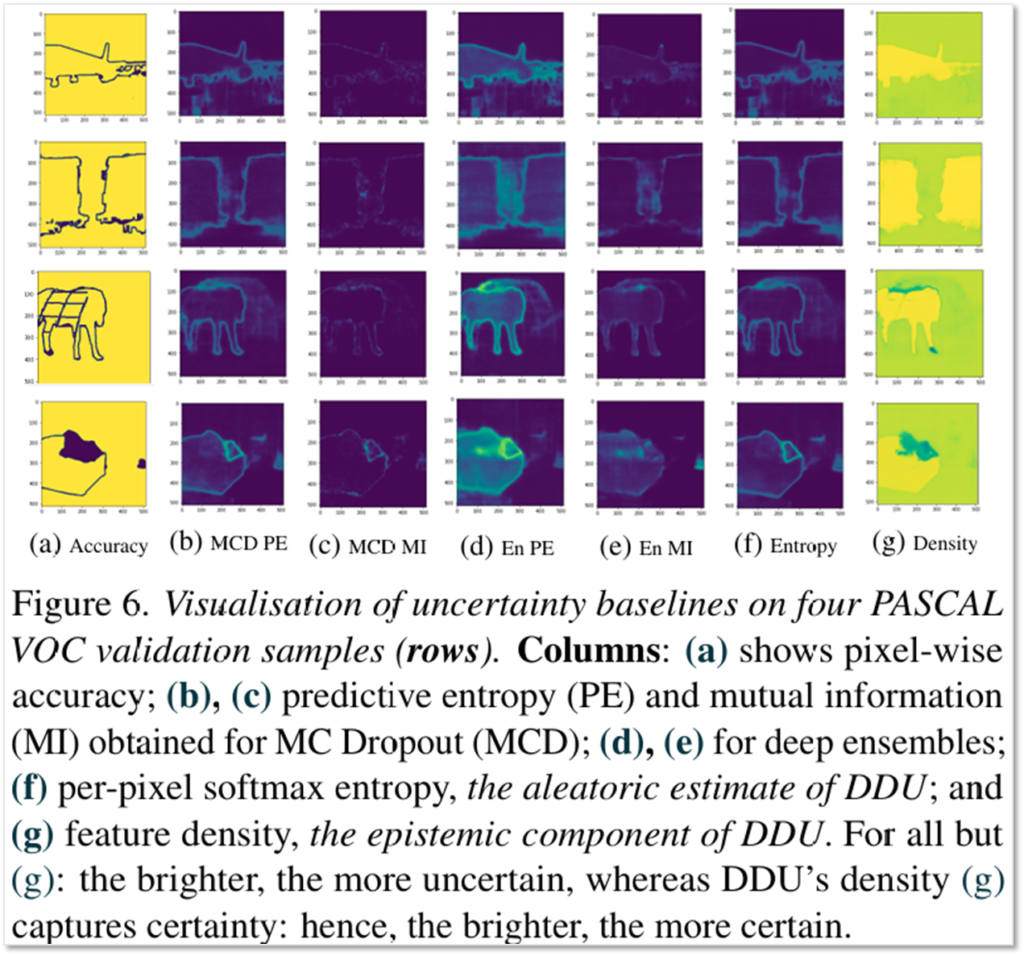
본 논문의 교신 저자인 Yarin Gal 교수님의 유명 논문(arxiv)은 비전 테스크에서 uncertainty를 어떻게 이해할 수 있는지 보였는데요, 해당 논문에서도 Semantic segmentation을 수행하고 uncertainty를 시각화하여 두 구분된 uncertainty가 의미적으로 다름을 보였습니다. 이는 DDU로 모델링된 불확실성이 비전 테스크에서도 효과적으로 사용 가능함을 시사합니다. 위의 이미지에서 f와 g가 DDU로 모델링된 불확실성이며, f는 aleatoric uncertainty로 시스탬 내재적인 무작위성으로 인해 엣지 라인에 대한 활성화가 높으며, g가 모델링하는 epistemic uncertainty는 지식 부족에 의한 불확실성으로 엣지보다는 물체 내부의 context 영역에 활성화가 높음을 확인할 수 있습니다.
참조
[1] DUQ: Joost van Amersfoort, Lewis Smith, Yee Whye Teh, and Yarin Gal. Uncertainty estimation using a single deep deterministic neural network. In International Conference on Machine Learning, pages 9690–9700. PMLR, 2020. 2, 3, 4, 6, 8, 12, arxiv
[2] SNGP: Jeremiah Zhe Liu, Zi Lin, Shreyas Padhy, Dustin Tran, Tania Bedrax-Weiss, and Balaji Lakshminarayanan. Simple and principled uncertainty estimation with deterministic deep learning via distance awareness. In NeurIPS, 2020. 2, 3, 6, 8, 12, 13, 15, 21, arxiv
본 논문은 불확실성 근사 추정을 위한 베이스라인을 제시하는 논문이였습니다. 이름 그대로 simple한 baseline을 제시하는 논문인데요, 특히 epistemic uncertainty과 aleatoric uncertainty를 개별적으로 모델링이 가능함을 보임으로써, 근사를 통한 추정의 하위 테스크(Active Learning, Ood Detection)에 대한 활용 가능성을 높인 연구로 이해한다면 좋을것 같네요. 결정론적 딥러닝(일반적으로 우리가 사용하는 딥러닝) 모델의 uncertainty 근사하는 방법의 동향이 이렇구나(uncertainty를 더욱 세분화하도록 분류하려는 시도가 있구나) 정도로 읽어보시면 재미있을 것 같습니다. 감사합니다.
Spectral Normalization의 경우 [2]에서 다루어진 방법으로 이후에 다른 리뷰에서 다루어보려고합니다.. 감사합니다