오늘은 ACL 학회의 Finding 섹션에서 발표된 논문을 소개하겠습니다. Finding 섹션은 프로시딩 되지 않은 논문 중 아깝게 떨어진 논문을 의미한다고 하는데요, ACL 학회는 NLP 분야의 탑티어 학회이기도 하고, 아마존[논문링크]에서 발표된 논문이라 의미가 있다고 생각하여 소개하게 되었습니다. 그럼 리뷰를 시작하겠습니다
소개.

오늘 소개드릴 논문의 목적을 요약하면 [그림1]과 같습니다. 하이라이팅된 부분의 기호 설명으로 a는 프롬프트이고 x는 데이터, y는 정답 라벨을 의미하는데요, 프롬프트 a를 잘 활용해 LLM을 잘 보정(calibration)하여 LLM을 최대한 잘 이용해보자는 것입니다.
지난 세미나에서, 최근 연구들은 빈도주의적 딥러닝 모델에 드롭아웃 및 모델 앙상블 기법을 적용하여, 베이지안적인 관점에서 불확실성을 추정할 수 있음을 소개해 드렸습니다. 그러나 대형모델의 경우 해당 기법을 적용하여 최적화 하기에 연산량이 많이 발생한다는 문제가 있죠. 또한 최신 대형모델들은 API 형태로 제공되는 경우가 있어, 이러한 재학습 기법을 적용하기 힘든 경우가 있습니다. 본 논문은 이러한 조건을 갖는 LLM에서도 불확실성을 추정할 수 있도록 다양한 프롬프트를 앙상블하는 방법을 제안합니다. 제안하는 방법을 통해 모델의 불확실성을 추정하고, well-calibrated된 결과를 얻을 수 있음을 실험과 함께 보인 논문입니다.
실험은 4가지 타입(감정 분석, 주제 분류, 의미적 유사성 분류, 스팸 분류)의 NLP 분류 테스크에 대해 진행되었습니다. 목표는 well-calibrated 된 결과를 얻는것이며, well-calibrated의 의미는 예측에 대한 확신도와 정답을 맞출 확률이 동일해지는 것을 의미합니다. 수식적으로는 [수식1]과 같이 표현할 수 있는데, 새로운 데이터 {x, y∗}에 대해서 실제 모델이 정답으로 예측할 확률-우항-이 예측의 확신도, 예측의 발생 확률-좌항-과 동일해야한다는 의미입니다. 실험 결과 제안하는 방법이 LLM의 불확실성 정량화를 기존 대비 개선했다고 합니다. 정리하면, 제안 방법론은 프롬프트 앙상블을 통해 연산량의 증가 없이 API 형태로 제공되는 Black-box LLM에서 불확실성을 가능하게하였는데요, 이어서 용어 정리등을 위한 문제정의를 다루겠습니다.
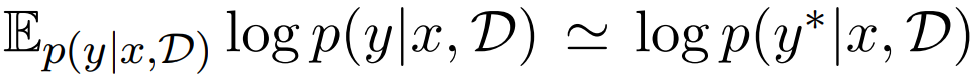
문제정의.
앞서서 본 논문이 프롬프트 다양화로 앙상블을 구현하여 모델의 불확실성을 추정하는 방법을 제안하는 방법이라고 말씀 드렸습니다. 이때 불확실성이 왜 추정되어야 할까요? 딥러닝에서 불확실성을 추정해야 하는 대표적인 목적은 다음과 같습니다: know when they don’t know. 서비스에서 모델의 예측을 활용하기 위해서는 해당 예측을 어느 정도로 신뢰해도 되는 지를 알아야 합니다. 신뢰할 수 없는 예측이라면 사용하지 않는 것이 서비스의 안정성을 높일 수 있기 때문입니다.
하지만 딥러닝의 메커니즘으로는 불확실성을 추정하는 것이 불가능합니다. 분류 문제에서 예측의 출력값인 logit을 확률로 해석하는 경우도 있으나, 학습 데이터의 라벨값에 확률 정보가 없기 때문에-one-hot 분포이기 때문에- 확률(혹은 불확실성)에 대한 정량화가 근본적으로 불가능합니다. 이에 대한 대책으로 Bayesian neural networks(이하 BNN)이 제시되고 있는데, BNN은 예측에 대해 불확실성을 정량화하는 방법이 확립되어있기 때문입니다. 본 논문 또한 BNN의 메커니즘을 통해 기존 불확실성을 산출할 수 없었던 LLM을 불확실성을 산출할 수 있도록 개선한 것입니다.
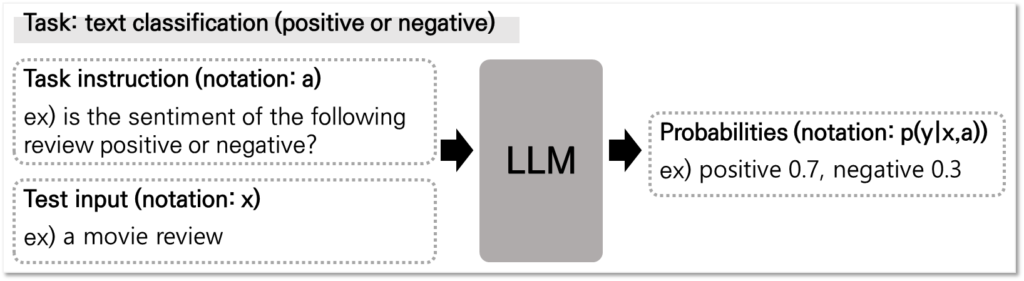
그렇다면 이러한 설계를 가진 LLM에서는 불확실성을 어떻게 산출하게 될까요? 우선 본 논문에서 정의한 LLM의 기본적인 동작과정은 [그림2]와 같습니다. 테스크에 대한 정보를 담은 Task instruction(이하 a)과 Test input(이하 x)를 함께 입력으로 LLM에 제공합니다. 즉 영화 리뷰의 긍부정 분류 테스크에서 LLM 입력의 형식은 “is the sentiment of the following review positive or negative? {review}”와 같습니다. 이후 LLM은 입력에 대한 예측을 logit 벡터([그림2]의 0.7, 0.3)와 함께 생성합니다. 나이브하게는 해당 예측된 logit을 확률로 해석하기도 합니다. 그러나 동시에 *overconfidence와 같은 이유로 logit을 확률값으로 해석하기 어려움이 꾸준하게 문제로 제기되고 있는 실정입니다. 본 논문은 기존 LLM의 불확실성 산출방식을 개선하기 위해 Task instruction, a를 다양화 하여 bayesian 관점의 해석으로 보다 정확한 불확실성을 산출하고자 합니다.
*overconfidence: 분류 문제에서 one-hot vector 등을 target으로 학습하여, 예측된 logit이 예측의 확신도를 충분히 반영하지 못하고 특정 값만을 높은 값으로 예측하게 되는 현상.
설계.
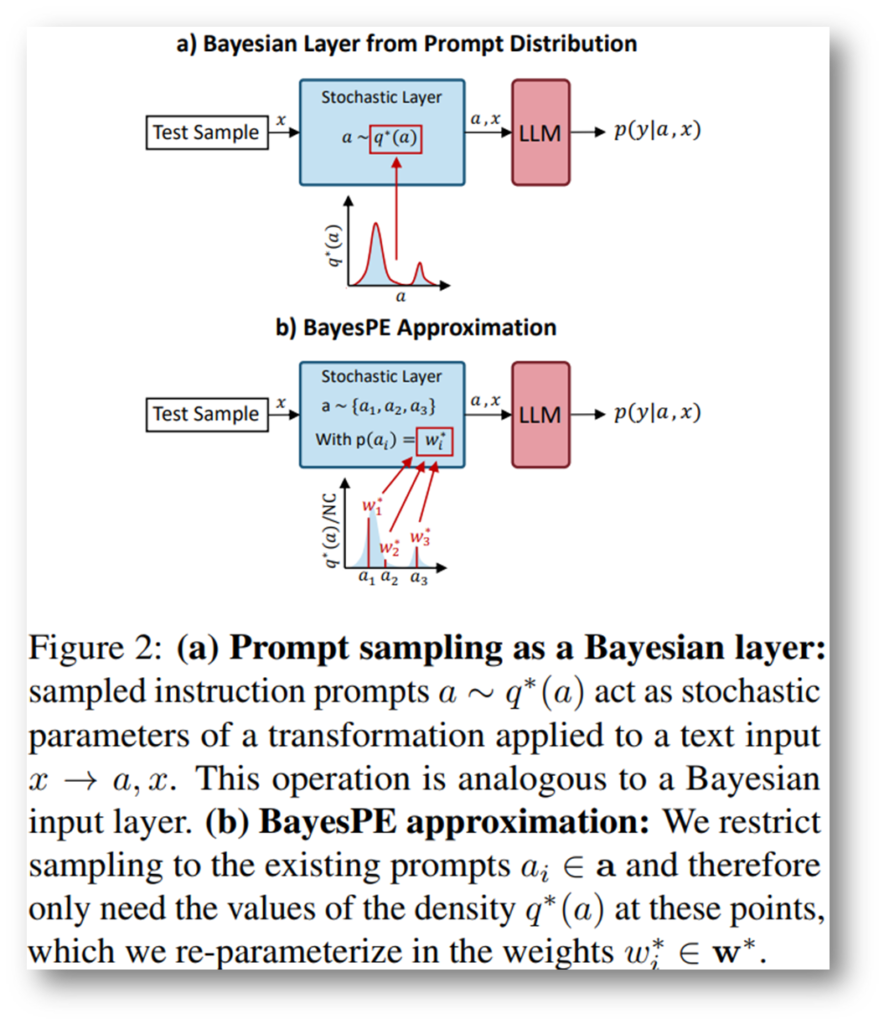
본 논문이 제안하는 방법의 이름은 Bayesian Prompts Ensembles, 줄여서 BayesPE 입니다. 이름처럼 프롬프트를 앙상블 하는 방법으로 불확실성 추정을 가능하게 합니다. 제안 방법의 특징은 [그림3]의 (b)에서 파란색 박스 부분, Stochastic Layer,입니다. 이는 이용가능한 프롬프트(notion: a_i)의 가중치(notion: p(a_i), w_i)를 생성하여 실제 데이터의 발생 확률(notation: p(a|D))을 잘 모사하도록 설계하는 것입니다. (프롬프트를 직접 생성할 수도 있지만, 본 논문에서는 불확실성 추정이라는 목적에 맞게 미리 정의된 프롬프트 배치에서 하나의 프롬프트 a_i를 입력으로 이용하며, 직접 생성하는 방법은 이후 과제로 남긴다고 밝혔습니다.) [그림3]를 통해 제안하는 방법이 Stochastic Layer에 프롬프트의 가중치를 추정하는 BayesPE를 설계하여 기존 Bayesian layer를 통한 베이지안 설계를 모사하였음을 설명했는데요, 해당 구조의 학습 방법에 대해 조금 더 자세하게 알아보겠습니다.
설계의 최종 목적은 p(a_i)를 잘 설계하여 p(a|D)를 모사할 수 있는 Stochastic Layer를 설계하는 것입니다. 해당 문제를 해결하기에 앞서 사후확률을 모사하는 기존 접근법을 소개하겠습니다. 사후확률인 p(a|D)의 분포를 구하는것은 일반적으로 연산량이 매우 크기 때문에 다루기 용이한 함수 q(a)로 근사함을 가정합니다. 함수의 근사에는 변분 추론(Variational Inference)이 주로 이용되며, 아래의 [수식2]과 같은 ELBO 최적화 문제로 다루게 됩니다. 근사함수인 q(a)와 실제 사후분포인 p(a|D)의 KL 거리가 가까워지도록 q(a)를 설계하게 되며, 해당 프로세스로 최적화된 q*(a)가 p(a|D)의 대체분포로 사용되게 됩니다. 즉, 아래의 수식을 통해 우리는 설계할 가중치(p(a_i))의 정답지 q*(a)를 설계할 수 있는것 입니다.
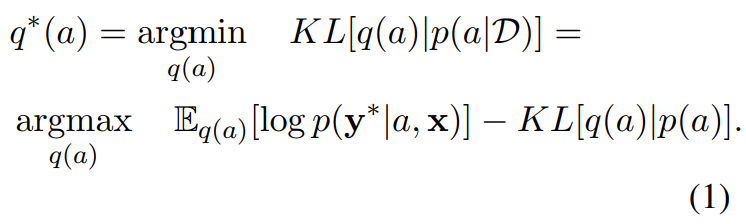
논문의 최종 목적은 batch 내의 요소 a_i의 가중치(p(a_i))를 설계하여, p(a|D)를 근사하는 것입니다. 즉 P(a_i)=w가 p(a|D)를 근사하도록 수식을 설계해야합니다. 해당 목적을 달성하기 위해 기존 변분추론의 수식인 [수식2]를 활용하여 아래의 [수식3]을 설계합니다. [수식2]와 [수식3]의 뺄셈으로 결합된 두 항(term)을 보면 의미적으로 동일함을 확인할 수 있는데, 우선 첫번째 항을 보면 특정 분포(q(a) or w)에서 정답(y*)를 옳게 예측할 가능성을 의미하며, 둘째 항은 특정 분포(q(a) or w)가 정답분포(p(a) or one-hot distribution)와 일치하는 정도를 의미합니다. 즉, 기존의 변분추론 방식인 [수식2]를 p(a_i) 기반의 수식으로 차용하므로서 학습을 설계한 것이며, 해당 수식을 최적화하면 가중치를 통해 실제 분포 p(a|D)를 근사하는 것과 동일합니다.

이후 모델의 추론 방법은 기존 베이지안 방법과 동일합니다. [수식3]을 통해 가중치 w_i(=p(a_i))를 설계한다면, 입력 x에 대한 LLM의 확률 분포는 [수식4]와 같이 구할 수 있으며, N개의 사전정의 된 Task instruction(a_1, a_2, … a_N)을 활용하여 예측을 산출하고(notation: p(y|a_i, x)) 이를 w_i를 통해 가중합(ensembles)하여 calibration된 예측 확률값(notation: p(y|x))를 산출하는 것입니다.
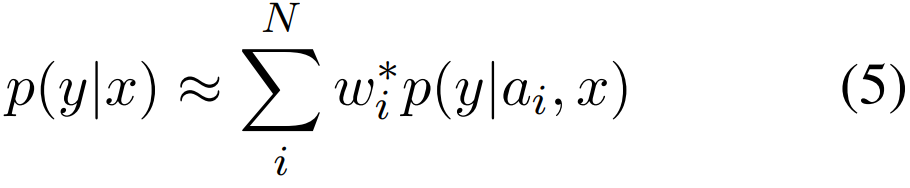
실험.
실험은 앞서 언급된 4가지 NLP 분류 테스크(감정 분석, 주제 분류, 의미적 유사성 분류, 스팸 분류)에서 각각 2~3개의 데이터셋으로 진행되었으며 Uncertainty calibration 검증을 위한 6개의 지표(NLL, AUC, ECE, MCE, Brier, F1)에 대한 성능이 리포팅 되었기에 Appendix를 포함하여 24페이지로 구성됩니다. 따라서 모든 실험 결과를 해당 리뷰에서 다루지는 않고, 실험 세팅과 전반적인 해석만을 다루어 여러분이 실험 결과를 직접 해석할 수 있게 하고자 합니다.
#– 실험 세팅
실험의 목적은 제안된 BayesPE가 모델의 예측을 잘 calibration 할 수 있는지를 평가하는 것입니다. 먼저 실험에 사용된 비교 방법론은 다음의 세가지 입니다. 비교 방법론 없이 자가검증을 수행했음을 알 수 있습니다.
- Standard: LLM을 활용하여 하나의 Task instruction(a_i)를 활용하여 x에 대한 예측을 수행한 결과. 이때, a_i는 사전 정의된 프롬프트 집합(=Task instruction 집합)에서 무작위로 선별됨.
- Ensemble: LLM을 활용하여 사전 정의된 모든 Task instruction을 활용해 x에 대한 예측을 수행하고 합산한 결과.
- Best: LLM을 활용하여 사전 정의된 모든 Task instruction을 활용해 x에 대한 예측을 수행했을 때, 가장 정확도(validation accuracy)가 높은 a_i를 통해 예측을 수행한 결과.
비교 방법론이 없는 대신 다양한 평가 지표로 검증을 시도했는데, 지난번 리뷰했던 Make me a BNN[논문링크]의 실험 평가 지표와 유사한 지표를 사용한 것으로 보아, 해당 분야에서 Uncertainty 산출에 대한 효과를 검증하는데 많이 사용되는 지표임을 알 수 있습니다. 앞서 언급한 것처럼 6가지 지표로 평가되었으며 5개의 지표(negative log-likelihood (NLL), ROCAUC score (AUC), expected calibration error (ECE), maximum calibration error (MCE) and Brier score (Brier))는 Uncertainty calibration 정도를 평가하기 위한것이고, F1-score(F1)는 해당 접근방식을 통해 기존 LLM 성능이 저해되는지를 확인하기 위한 보조적인 지표입니다.
실험은 총 10가지의 NLP 데이터셋에 대해 수행되었으며, 그 정보는 아래와 같습니다.
- 감정 분석(sentiment analysis tasks, 3종): Amazon Reviews, Imdb, SST-2
- 주제 분류(topic modeling tasks, 3종): DBPedia 14, Yahoo Answers, TREC
- 의미적 유사성 분류(semantic relation tasks, 2종): MRPC, SNLI
- 스팸 분류(spam detection tasks, 2종): SMS, YouTube
또한 실험에 사용된 LLM은 5개의 open-source LLMs을 활용하였으며, 자세한 정보는 [표1]과 같습니다. 또한 Task instruction 집합을 생성하기 위해서는 테스크당 하나의 initial prompts를 생성([그림4] 참조)하고, 이를 gpt-3.5-turbo를 통해 어휘변용(paraphrase)하여 태스크 당 10개의 instruction을 생성했습니다.

#– 실험 결과
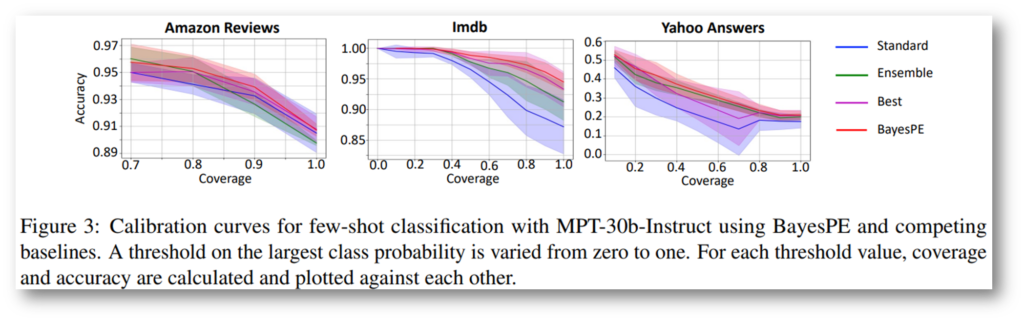
[그림5]는 논문의 주요 실험중 하나로, accuracy와 coverage를 통한 calibration curves 결과이며, coverage는 주어진 임곗값으로 필터링한 예측 샘플을 의미합니다. 즉 해당 시각화에서 높은 coverage(x축)일 경우 높은 accuracy(y축)에 값이 위치하는 것이 이상적인 분포입니다. 시각화를 통해 제안하는 BayesPE(붉은색)이 임곗값으로 필터링시에 학습 성능이 가장 높게 위치하며, 예측 스코어(logit, 확신도)와 모델의 실제정확도가 잘 calibration 되었음을 확인할 수 있습니다.
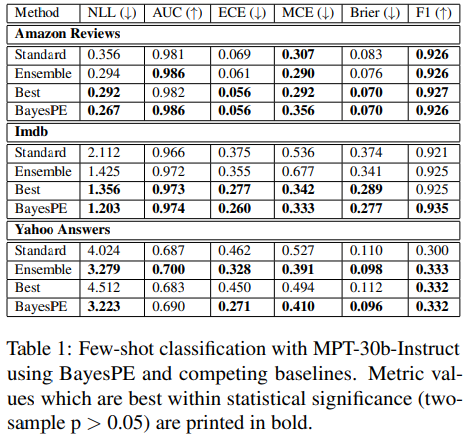
다음은 정량적 평가의 일부인데요, 논문에서 전반적으로 모든 평가지표에서 제안하는 BayesPE가 LLM 정확도 성능(F1)의 저하 없이 uncertainty에 대한 평가가 개선되었다고 정리합니다. 이 외에도 [표1]에 언급된 모든 LLM에 대한 다양한 데이터셋에 대한 성능은 논문의 appendix에 리포팅되어 있으니, 필요 시 참고하시길 바랍니다.
마무리.
본 논문은 프롬프트 풀에서 각 요소의 가중치를 추론하여, well-calibrated 된 예측을 수행하는 BayesPE 방법을 제안합니다. 해당 논문을 통해 최신 LLM의 Black-box 시나리오-입력에 대한 결과만을 생성하는-에서도 불확실성을 추론할 수 있게 되었습니다. 또한 입력값 변경으로 불확실성 추론이 가능하여 기존에 재학습을 요구하는 방법보다 연산이 효율적이라는 장점 있었습니다.LLM의 calibration에 관심이 있다면 해당 논문을 확인해보는 것도 좋을 것 같네요. 감사합니다.
앞선 리뷰에서 bayesian 해석으로 예측에 대한 두가지 uncertainty( Epistemic uncertainty, Aleatoric uncertainty)를 산출할 수 있다고 말씀드렸습니다. 해당 리뷰에서 Uncertainty란 Model uncertainty(= Epistemic uncertainty)를 의미합니다. LLM에서 안전성을 위한 Uncertainty를 언급할 때, 주로 Model uncertainty를 활용하는 것 같은데, 그 이유는 아직 확인하지 못했네요. 앞으로도 대형모델에서 베이지안 접근법의 유효성을 다루는 논문을 더욱 찾아보고자 합니다. 이상으로 이번 리뷰는 마치겠습니다. 감사합니다.