안녕하세요 오늘 제가 리뷰 할 논문은 Batch Normalization에 대해 다뤄 NIPS 2018에 게재된 논문입니다. 제가 최근에 URP 1주차 인공지능 기초를 준비하며 제가 Batch Normalization에 대해서 잘못 알고 있다는 점을 알게 되어 더 학생들을 알려줘야하는 입장에서 제가 제대로 알고 있지 않으면 제대로 설명해 줄 수 없겠다 생각되어 읽게된 논문입니다. 많은 연구원님들이 Batch Normalization에 대해서는 잘 알고 계시겠지만, 그래도 오랜만에 복습한다는 느낌으로 또 만약에 저처럼 잘못 알고 있는 내용이 있었다면 제대로 알고 갈 수 있는 기회가 되었으면 좋겠습니다.
Batch Normalization
먼저, 논문 리뷰에 앞서 Batch Normalization의 개념을 간단하게 짚고 넘어가겠습니다. Batch Normalization은 gradient descent를 통한 학습 과정에서 각 배치 단위 별로 데이터의 평균과 분산을 이용해 정규화를 해주는 방법을 말합니다. 이때 데이터의 평균과 분산을 구하고 scaling 파라미터 \lambda와 bias 파라미터 \beta를 이용하여 정규화를 진행하고 이때 두 파라미터는 backpropagation을 통해 학습합니다.
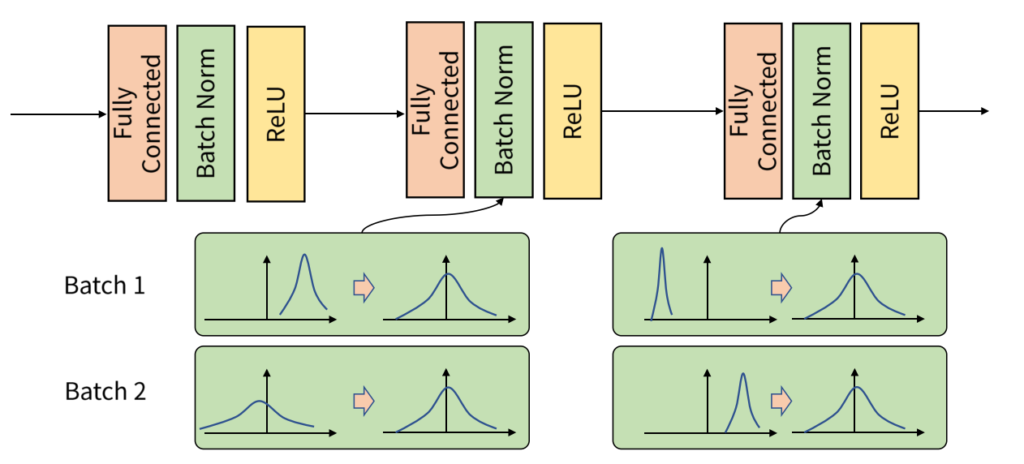
위 그림 1은 Batch Normalization을 보여주는 그림으로 각 배치별 데이터의 분포가 서로 다른 분포를 가지더라고 정규화를 통해 배치 내 데이터의 분포를 안정화해주는 모습을 보여줍니다.
Introduction
Batch Normalization은 일반적으로 Deep Neural Network(DNN)의 학습과정에서 더 빠르고 안정적으로 수렴할 수 있도록 사용하는 기법입니다. 저자는 이러한 Batch Normalization이 널리 사용되고 있음에도 불구하고 아직 Batch Normalization이 왜 효과적인 지에 대한 정확한 이유는 아직 잘 모르고 있다고 지적합니다. 논문이 게재된 연도는 2018년으로 Batch Normalization이 처음 제안된 2015년으로부터 약 3년이 지난 후입니다. Batch Normalization이 처음 제안될 때에는 Internal Covariate Shift문제를 해결했기에 학습에 효과적이라고 설명합니다.
본 논문에서 저자는 이러한 각 계층에서의 입력 데이터의 분포의 안정성이 Batch Normalization의 성공에는 크게 기여하지 않는 다는 것을 보여줍니다. 대신에 Batch Normalization이 그것보다 조금 더 근본적인 영향을 끼친다는 것을 밝혀냈습니다. 저자는 Batch Normalization이 최적화 지형(Optimization Landscape)을 더 smooth하게 만들고 이로 인해 gradient가 보다 안정적으로 동작하여 빠른 학습을 가능케한다는 점을 밝혀냈습니다.
Batch Normalization이 처음 제안될 때 Batch Normalization이 학습의 속도와 안정성에 도움을 주는 이유는 Internal Covariate Shift(내부 공변량 변화)를 해결했기 때문이라고 설명하고 있습니다. Internal Covariate Shift(ICS)는 이전 계층에서의 가중치 업데이트로 인해 다음 계층이 받는 입력 분포의 형태가 달라지게 되고 이러한 달라진 입력 형태의 분포가 계층을 지나면서 누적되어 변화가 크게 달라지는 문제를 말합니다. 이렇게 계층 별 입력 데이터의 분포가 달라지는 것이 학습을 방해하기 때문에 이와 같은 ICS문제를 해결하는 방법이 Batch Normalization이라고 일반적으로 알려져 왔지만, 저자는 구체적으로 ICS가 어떻게 학습 과정을 방해하고 Batch Normalization이 해결하는 지에 대한 메커니즘은 확실하지 않다고 지적합니다.
따라서 저자는 이러한 Batch Normalization과 ICS와의 관계를 심층적으로 분석했고 결과적으로 기존의 설명과는 다른 사실들을 발견했습니다. 논문은 ICS와 Batch Normalization과의 관계 그리고 Batch Normalization의 실제 역할에 대한 분석으로 구성되어 있습니다.
결론부터 말씀드리면 저자가 말하길 Batch Normalization이 내부 공변량을 줄이는 것 사이에는 명확한 연관성이 없고, 오히려 실제로 Batch Normalization이 ICS를 줄이지 못할 수도 있다고 주장합니다. Batch Normalization이 학습에 효과적인 이유는 학습을 위한 optimization을 위한 landscape(최적화 지형)을 smooth하게 만들어 gradient가 더 예측 가능해지고 이를 통해 learning rate의 범위를 더욱 넓게 사용할 수 있기에 빠른 수렴을 유도한다고 말합니다. 또한 이러한 smoothening 효과가 Batch Normalization만의 효과가 아닌 다른 정규화 방법들도 유사한 개선효과를 보인다는 것을 보입니다.
Batch Normalization and Internal Covariate Shift
Batch Normalization(이하 배치 정규화, BN)은 결국 학습 과정에서 특정 계층에 입력되는 배치 단위의 분포를 안정화하는 것을 목표로 하는 기법입니다. 구체적으로는, 네트워크의 추가적인 계층을 더하여 각 activation의 분포에서 평균과 분산을 각각 0과 1이 되도록 정규화합니다. 그 후 모델의 표현력을 유지하기 위해서 학습 가능한 파라미터 (scaling, bias)를 사용해 정규화된 입력을 적당히 scaling하고 shift합니다. 이는 이전 계측의 비선형 활성화 함수를 적용하기 전 단게에 수행됩니다.
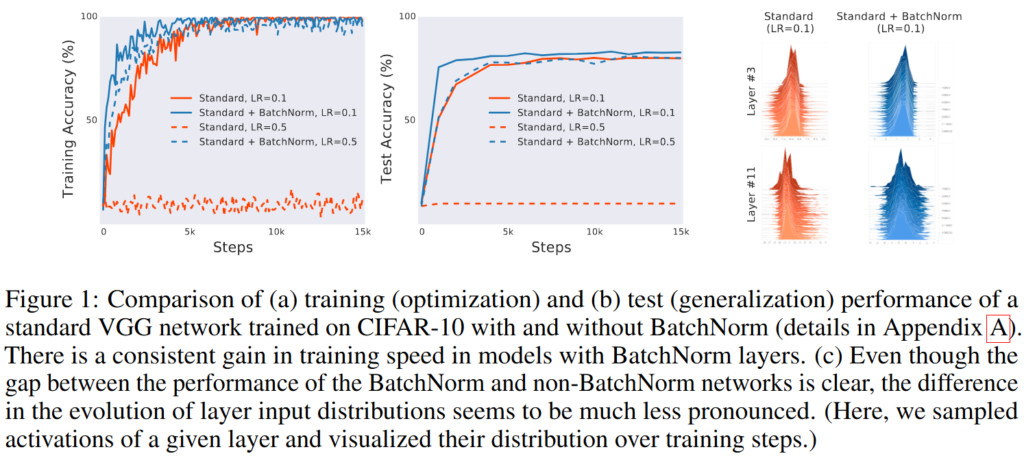
Figure1 (a)는 CIFAR-10 데이터셋에서 배치 정규화를 적용한 VGG 네트워크와 적용하지 않은 네트워크의 최적화 성능을 보여주는 그림입니다. (b)는 위의 배치 정규화를 적용한 VGG 네트워크와 적용하지 않은 네트워크의 일반화 능력을 보여주는 그림입니다. (c)는 배치 정규화가 적용된 네트워크와 적용되지 않은 네트워크의 입력 분포의 차이를 보여주는 그림입니다. 그림에서도 알 수 있지만, 일반적으로 배치 정규화가 해결했다고 말하는 ICS의 문제가 거의 없다시피한 모습을 확인할 수 있습니다. 배치 정규화를 적용했을 때와 적용하지 않았을 때가 거의 비슷한 분포를 보여주고 있습니다.
따라서 저자는 배치 정규화가 분명히 학습 수렴의 속도 및 안정성에 차이를 만드는 것은 분명하지만, 그것이 단순히 ICS를 줄이는 데에서 오는 것인지에 대한 의문을 제기합니다.
Does Batch Norm’s performance stem from controlling Internal Covariate Shift?
저자는 배치 정규화가 계층의 입력의 평균과 분산을 제어하여 성능이 좋아지는 것이 맞는 지를 확인하기 위해 의도적으로 노이즈를 첨가하여 계층에서의 입력 분포가 흔들리도록 조정하여 비교하는 실험을 진행합니다.
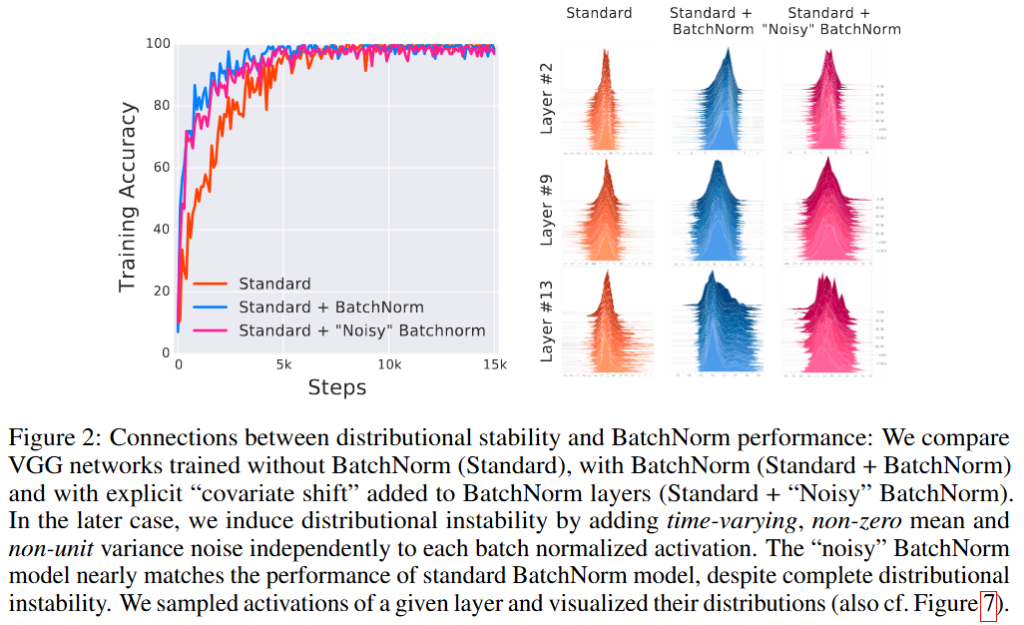
Figure2에서 사용한 3개의 네트워크는 일반적인 배치 정규화를 사용하지 않은 네트워크와 배치 정규화를 적용한 네트워크 그리고 배치 정규화를 적용한 후에 노이즈를 첨가한 네트워크 총 3개의 네트워크를 비교함으로 정말 입력 분포를 안정화하는 것이 효과가 있는 것인지를 검증합니다. 만약에 ICS를 해결하여 입력 데이터의 분포가 안정화되는 것이 모델의 수렴 속도, 안정성에 도움이 되는 것이라며 배치 정규화를 적용하지 않은 네트워크와 배치 정규화를 적용하고 노이즈를 첨가한 네트워크가 모두 배치 정규화를 적용한 네트워크보다 떨어지는 성능을 보여야합니다. 하지만, 실제 실험 결과를 확인하면 노이즈를 추가한 네트워크의 성능이 배치 정규화를 적용한 네트워크보다는 떨어지기는 하지만, 큰 차이를 보여준다고 말할 수 없습니다. 배치 정규화를 적용하지 않은 네트워크와 비슷한 성능을 보이는 것이 아니라 적용하지 않은 네트워크보다는 훨씬 좋은 성능을 보여주기 때문입니다.
즉, 저자가 위 실험을 통해 강조하는 점은 배치 정규화를 적용한 이후에는 의도적으로 노이즈를 첨가하는 행위를 통해 입력 데이터의 분포를 변경해주어도 배치 정규화를 적용하지 않은 네트워크보다 학습이 더 잘 진행된다는 점입니다. 이를 통해 저자는 ICS를 해결하는 것만으로는 배치 정규화의 진짜 효과를 설명하기 어렵다고 강조합니다.
Is Batch Normalization reducing internal covariate shift?
위의 실험 결과를 통해 ICS와 학습의 성능 사이에는 직접적인 연결고리가 없을 수 있다는 점을 확인했습니다. 저자는 기존에 정의된 ICS의 개념보다도 더 광범위한 어떠한 현상을 포괄하는 방식으로 정의할 수 있을 것이라 추측하고 기존의 개념을 점검합니다.
학습 과정은 하나의 최적화 문제입니다. 이러한 최적화 문제는 손실 함수에 영향을 미치는 모든 계층들의 파라미터를 점진적으로 개선해나갑니다. 즉, 이전의 계층의 파라미터가 개선되었다면, 이전 계층으로부터의 입력이 바뀔 수 있습니다. 이것이 기존 ICS의 핵심 직관입니다. 즉, 학습이 원활히 진행되기 위해서는 이전 계층의 업데이트로 인한 입력이 크게 변하지 않아야한다는 것을 의미합니다.
저자는 배치 정규화가 성공을 거둔 이유는 결국 최적화 문제와 깊은 관련이 있음을 가정하고 학습 하는 과정에서 gradient를 통해 가중치가 얼마나 조정되어야 하는 지를 측정함으로 이것이 실제로 ICS와 얼마나 연관이 있는지를 체크합니다.
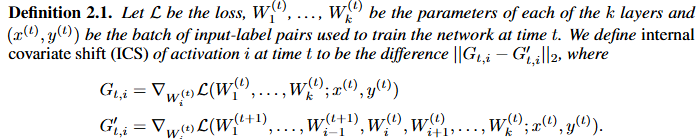
수식을 간략하게 설명드리면 ICS를 ||G_{t, i} - G'_{t, i}||_2로 정의하고 G_{t, i}는 모든 계층이 동시에 업데이트될 때의 gradient이고 G'_{t, i}는 이전 계층을 먼저 업데이트한 후 계산했을 때의 gradient입니다. 만약에 배치 정규화가 정말 ICS를 줄인다면, ||G_{t, i} - G'_{t, i}||_2값이 크게 감소해야합니다. 위 값을 구하여 비교하는 것으로 실제로 배치 정규화가 ICS를 얼마나 줄일 수 있는 지를 검증합니다.
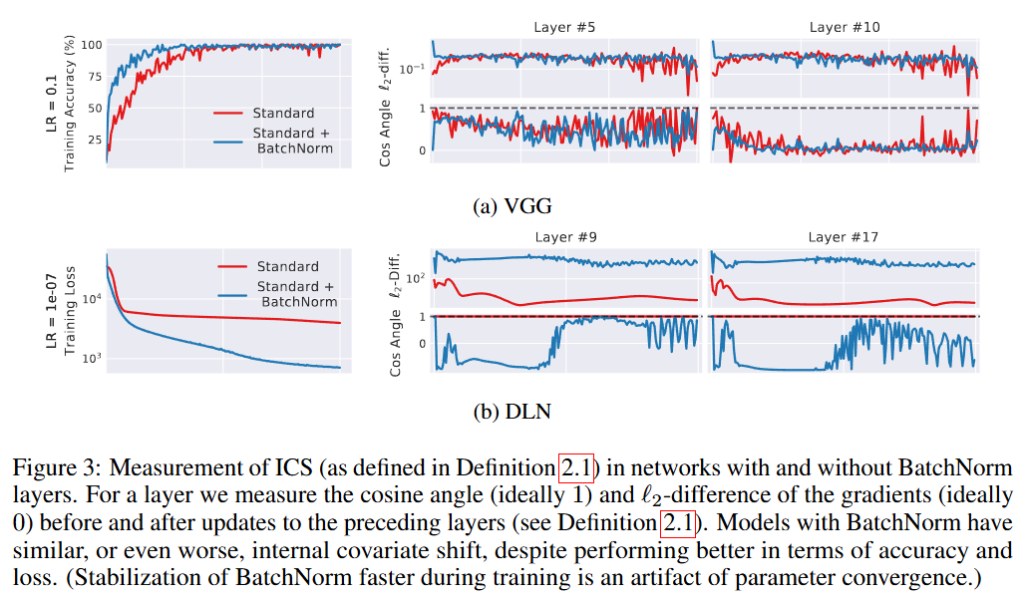
Figure3은 배치 정규화가 있는 네트워크와 없는 네트워크에서의 ICS를 측정한 결과를 보여줍니다. 구체적으로는 gradient 벡터 사이의 코사인 각도와 L2거리를 통해 각각 1, 0에 가까울수록 방향, 크기의 차이가 적은 성질을 활용해 ICS를 측정합니다. 결과적으로 배치 정규화를 적용하는 것은 ICS를 확인했을 때에 ICS가 줄었다고 볼 수 없음을 지적합니다. 오히려 더 나빠지는 경우도 있음을 실험을 통해 보여줍니다. 즉, 배치 정규화가 각 계층의 입력 분포를 안정화한다는 일반적으로 알려진 통념과는 상반된 결과를 보여줍니다. 따라서 최적화의 관점에서 배치 정규화는 반드시 ICS를 줄이는 것은 아닐 수도 있다는 점을 보여줍니다.
이를 통해 저자는 배치 정규화 계층이 학습 중에 빠르게 안정된 것처럼 보이는 이유는 사실 파라미터가 최적화되는 과정에서 자연스레 발생하는 결과일 가능성을 제기하며 배치 정규화의 근본적인 작동 방식에 대한 의문을 제기합니다.
Why does Batch Normalization work?
초기 배치 정규화가 제안될 때에 언급된 부수적인 효과들은 다음과 같습니다.
- 기울기가 폭발 혹은 소멸하는 것 방지
- 하이퍼파라미터 설정에 강인함
- 활성화 함수의 saturation 영역 회피
위 관점들은 배치 정규화가 평균과 분산을 구하고 scaling, shift를 하는 과정에서 직관적으로 생각할 수 있는 효과들입니다. 하지만, 위 효과들은 본질적으로 배치 정규화가 왜 학습을 잘하게 되는 지에 대한 해답이 되지는 않습니다. 저자는 근본적으로 배치 정규화가 학습에 도움이 되는 이유는 optimization landscape를 smoothening하는 효과가 있기 때문이라고 주장합니다.
배치 정규화가 하는 가장 큰 작업 중에 하나는 네트워크의 입력, 출력 크기를 적절히 조절하여 loss와 gradient의 변화를 안정화하는 것입니다. 이는 optimization landscape를 smooth하는 역할을 한다고 볼 수 있고 loss와 gradient가 너무 빠른 속도로 급변하는 것을 막을 수 있고 계산된 gradient의 방향을 좀 더 신뢰할 수 있게 됩니다. 또한 큰 step으로 loss가 변하게 되더라고 더 큰 learing rate를 안전하게 시도할 수 있게 되어 학습 속도가 훨씬 빨라지고 하이퍼파라미터에 대한 민감도가 낮아지게 되어 모델을 tuning하기 쉬워진다고 합니다.
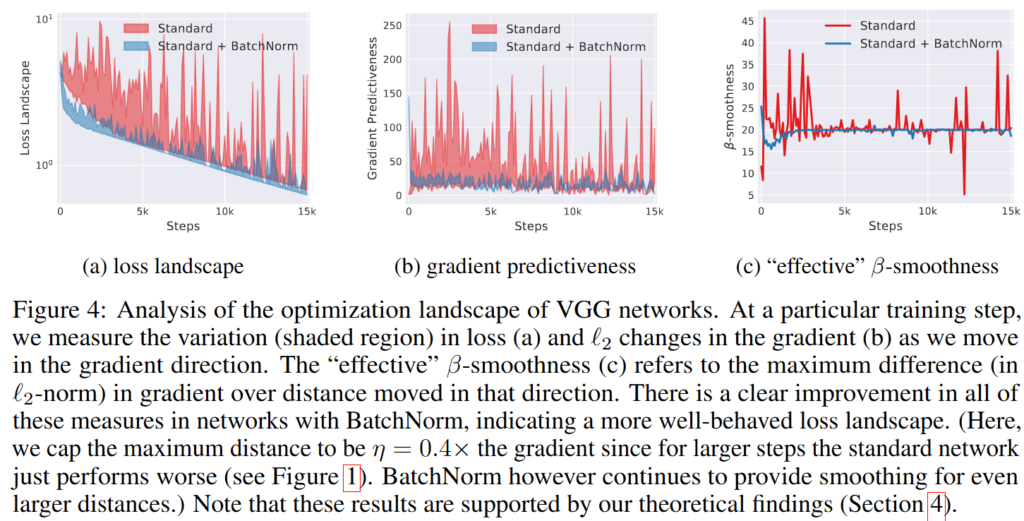
Figure4는 네트워크의 optimization landscape를 분석한 결과입니다. 특정 학습 step에서 저자는 gradient 방향으로 이동할 때에 발생하는 loss의 변화와 gradient의 L2 변화량을 측정합니다. (a), (b), (c)는 각각 loss, gradient의 L2변화, effective \beta-smoothness를 나타냅니다. effective \beta-smoothness는 해당 방향으로 이동했을 때의 gradient가 최대 얼만큼 변화하는 지를 보여줍니다.
모든 지표에서 배치 정규화를 적용한 네트워크가 배치 정규화를 적용하지 않은 네트워크보다 좋은 모습을 보이는 것을 확인할 수 있습니다. 즉 배치 정규화의 핵심은 optimization landscape를 smooth할 수 있고 이는 더 큰 learning rate를 가능케하며 하이퍼파라미터에 대한 의존성을 낮춘다는 것임을 주장합니다.
저자는 추가로 이러한 optimization landscape를 smooth하여 학습에 도움을 주는 것이 배치 정규화만의 특징인지도 점검합니다. 저자는 다른 여러가지 정규화 방법도 배치 정규화와 마찬가지로 실험을 통해 같은 효과를 가진다는 것을 확인합니다. 즉, 배치 정규화가 학습을 잘하게 만드는 것은 optimization landscape를 smooth하게 만드는 데에 있고 이는 배치 정규화만의 특징이 아닌 정규화의 효과임을 밝히며 배치 정규화의 성공은 ICS를 줄이기 때문이라기보다는 훨씬 포괄적인 “재파라미터화에 의한 optimization landscape smoothening”이 근본 원인이라고 주장합니다.
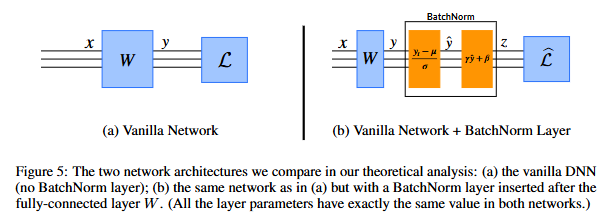
위 그림은 일반적인 네트워크의 구조와 배치 정규화를 적용한 네트워크의 구조를 보여주고 있습니다.
이후에 저자는 논문에서 저자의 주장을 수식을 통해 증명합니다. 수식에 대한 부분은 저자가 실험을 통해 보여주는 optimization landscape의 smoothening을 이론적으로 설명하기 위한 내용입니다. 제가 아직 제대로 이해하지 못하여 그림을 첨부하고 나중에 설명을 추가하도록 하겠습니다.
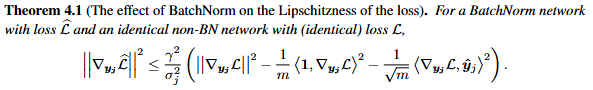
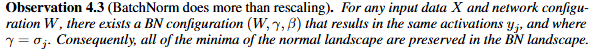
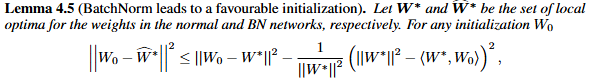
리뷰를 마치며 저는 이전부터 Internal Covariate Shift로 인한 데이터 분포의 차이로 인해 학습이 방해되고 이를 해결한 것이 배치 정규화 방법으로 알고 있었는데 새로운 견해을 알게되어 흥미로웠습니다. 저자가 당시 일반적인 통념이 잘못되었다는 것을 여러가지 실험을 통해 지적하고 자신의 생각을 설득력있게 주장하는 것 또한 인상적이었습니다.
감사합니다.
