[CVPR 2022] Incorporating Semi-Supervised and Positive-Unlabeled Learning for Boosting Full Reference Image Quality Assessment

안녕하세요. 박성준 연구원입니다. 오늘은 약간 색다른 task의 논문을 리뷰하게 되었습니다. 그렇기 때문에 이번 리뷰는 좀 더 자세하게 서술해보려 합니다.

최근 unlabeled 데이터들을 잘 활용하는 방법에 대해 관심이 생겨서 서베이 하던 중 positive 데이터와 unlabeled 데이터를 활용하는 positive-unlabeled learning에 대해 알게 되었습니다. positive unlabeled learning을 이진 분류가 아닌 다른 task에서 어떻게 활용하고 있는 지에 대해 알아보다가 해당 논문을 알게 되어 리뷰하게 되었습니다.

Full-Reference Image Quality Assessment (FR-IQA)

해당 논문은 학습 기반의 FR-IQA 연구입니다. Full-reference image quality assessment(FR-IQA)는 distorted image와 pristine-quality(높은 품질) reference(이미지)의 visual quality를 평가하는 task입니다. distorted 이미지의 경우 이미지를 손실 압축(png, jpeg 등) 혹은 down sampling 등의 원본 이미지에서 왜곡(distort)가 더해진 이미지를 의미합니다. 즉, 실제 높은 품질의 이미지와 낮은 품질의 이미지 사이의 차이를 비교함으로 낮은 이미지의 visual quality를 평가하는 task입니다. 낮은 품질과 높은 품질의 이미지 pair가 Mean Opinion Score(MOS)(여러사람이 이미지의 품질을 평가한 점수의 평균치)로 라벨링되어 있고, 두 이미지를 입력으로 받아서 낮은 이미지의 visual quality를 평가합니다. 아래 그림의 예시를 통해 pristine quality reference와 distorted image의 차이를 확인할 수 있습니다.

평가로는 여러가지가 사용될 수 있지만, 널리 사용되는 지표로는 크게 Peak Signal-to-Noist Ratio(PSNR) 혹은 Structural SIMilarity index(SSIM)이 많이 사용되어왔습니다. PSNR은 신호 대 잡음 비율을 측정하는 객관적 지표로, 원본 이미지와 손상된 이미지 간의 품질 차이를 수치화합니다. SSIM은 이미지의 구조적 유사성을 평가하는 지표로, 인간의 시각적 인식에 더 가까운 품질 평가를 제공합니다.

해당 논문에서는 Spearman Rank Correlation Coefficient(SRCC)와 Pearson Linear Correlation Coefficient(PLCC)를 사용합니다.

먼저, SRCC는 non-parametric 상관계수로 두 변수 간의 순위 관계를 측정합니다. 모델이 예측한 MOS와 실제 MOS 사이의 순위 관계가 얼마나 일치하는 지를 나타내는 지표로 \mathrm{SRCC} = 1 - \frac{6\sum d^2_i}{n(n^2 - 1)}의 공식을 통해 계산되며 d_i는 두 변수의 데이터 순위 차이, n는 데이터의 개수를 의미합니다.

PLCC는 두 변수 간의 선형 상관 관계를 측정합니다. 모델이 예측한 MOS와 실제 MOS 사이의 선형 상관도를 나타내는 지표로 \mathrm{PLCC} = \frac{\sum (x_i - \bar{x}) (y_i - \bar{y})}{\sqrt{\sum (x_i-\bar{x})^2 \sum (y_i - \bar{y})^2}}의 공식을 통해 계산됩니다. x_i, y_i는 두 변수의 데이터를 의미하고 \bar{x}, \bar{y}는 각 변수의 평균을 의미합니다.

SRCC는 MOS과 모델의 예측 점수와의 순위 관계를 따질 수 있지만, MOS의 절대적 차이를 고려하지 않고, PLCC는 MOS의 절대적 차이를 고려하기에 두 평가지표는 서로 보완적이므로 FR-IQA는 두 평가지표를 함께 사용하여 모델의 평가를 진행합니다.

Positive-Unlabeled Learning (PUL)

Positive-Unlabeled Learning(PUL)은 이름에서부터 직관적으로 알 수 있듯이 positive 샘플과 unlabeled 샘플을 활용한 학습을 말합니다. 일반적으로 이진 분류 task에서 활용되며 positive(P)와 negative(N)로 구성된 데이터 중 P에 대한 정보만을 가지고 있을 때에 사용합니다. 이진 분류가 아닌 task에서 활용되는 대부분의 PUL은 라벨링 코스트가 적음에도 불구하고 꽤 준수한 성능을 낸다를 주장하며 효율성을 강조합니다. 혹은 이진분류(foreground, background 분류)를 포함하지만 foreground의 정보만을 갖고 있는 task에서 추가적인 supervision으로 활용됩니다. 즉, PUL은 라벨링 코스트가 큰 task 혹은 task를 수행하는 과정에서 이진분류(foreground, background 분류)를 포함하는 task에서 활용됩니다. FR-IQA는 라벨링 cost가 커 PUL를 활용하는 전자에 속합니다.

Introduction

FR-IQA의 평가를 위해서 사용하는 MOS는 이미지에 대한 여러사람의 평가의 평균으로 여러사람이 라벨링을 진행해야하기에 라벨링 cost가 굉장히 큰 task입니다. 저자는 FR-IQA의 라벨링은 굉장히 힘든 반면에 라벨링 되지 않은 데이터를 구하는 것은 굉장히 쉽다고 말하고 있습니다. image-degradation, image-restoration 과정만을 거치는 것으로도 수집할 수 있기 때문입니다. 따라서 unlabeled 데이터를 활용하여 성능을 향상시키는 방법은 FR-IQA에서 중요한 과제 중에 하나입니다. 하지만, 라벨링된 데이터와 unlabeled 데이터 사이의 distribution inconsistency(분포 불일치)로 인해서 unlabeled 데이터에 outlier가 발생할 가능성이 높아 학습에 방해가 될 수 있다고 말하고 있습니다.

따라서 저자는 unlabeled 데이터를 활용하는 동시에 outlier의 부정적인 영향을 줄이기 위하여 semi-supervised learning(SSL)과 positive unlabeled learning(PUL)을 통합하는 Joint Semi-supervised and PU Learning(JSPL)을 제안합니다.

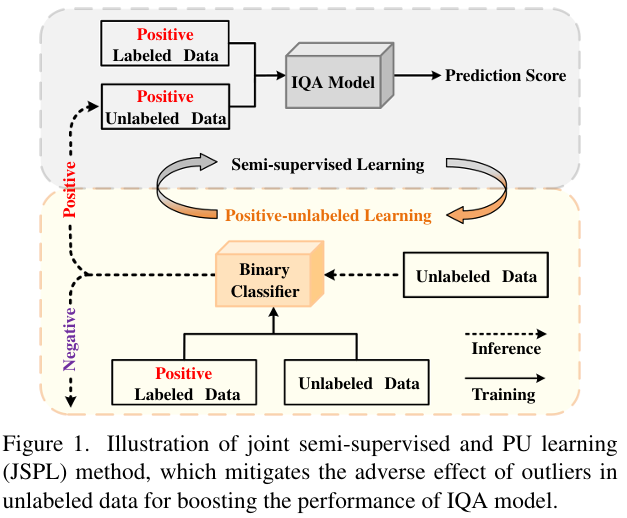
위 Figure 1.은 저자가 제안하는 JSPL의 구조를 보여줍니다. PUL은 positive와 unlabeled 데이터를 구분하는 데에 사용되지만 해당 논문에서 저자는 PU 학습을 MOS 주석이 없는 라벨이 없는 이미지 집합에서 outlier(즉, negative 샘플)를 식별하고 배제하는 데 활용됩니다. 추가로 PUL에 의한 예측은 신뢰도(confidence) 추정 역할도 수행할 수 있기에 저자는 PUL의 예측을 통해 SSL을 위해 가치 있는 positive unlabeled 데이터를 점진적으로 선택할 수 있도록 유도합니다. 저자는 이러한 JSPL구조를 통해 unlabeled 데이터를 학습에 사용할 수 있을 뿐만 아니라 FR-IQA 모델의 신뢰도도 올릴 수 있었다고 주장합니다.

IQA 모델은 저자는 Siamese(샴) 구조를 도입하고 pristine quality reference(이후에는 편의상 원본 이미지라고 하겠습니다)와 distorted image(이후에는 편의상 왜곡된 이미지라고 하겠습니다)를 입력으로 받아 특징을 추출하고 두 특징 사이의 difference map을 생성합니다. 저자는 difference map을 생성하는 과정에서 일반적인 유클리드 거리는 왜곡된 이미지와 원본 이미지의 공간적인 특징을 평가하는 데에 부적절하다고 언급하며 silced Wasserstein Distance(SWD)를 도입해 distance map을 생성합니다. SWD는 유클리드 거리에 비해 local 특징을 잡아낼 수 있어 적은 정렬 불일치에 대해 강건한 distance map을 생성할 수 있습니다. 마지막으로 저자는 Spatial Attention Module을 도입해 이미지 내 정보가 풍부한 지역에 더 집중할 수 있도록 모델링합니다. 이는 Human Visual System(HVS)(실제 사람의 시각 시스템)이 정보가 풍부한 지역에 먼저 집중하는 것에서 영감을 받았다고 합니다.

이에 따른 저자의 Contribution은 다음과 같습니다.

• SSL과 PUL을 통합하는 JSPL을 제안하여 MOS 라벨링이 되어있는 이미지와 라벨이 없는 이미지를 활용하여 FR-IQA 모델의 성능을 향상시켰습니다. PUL은 outlier를 제거하고 SSL을 위한 positive unlabeled 데이터를 점진적으로 선택하는 데 중요한 역할을 합니다.
• FR-IQA 모델에 Spatial Attention, SWD를 사용한 difference map를 이용하여 이미지 내 정보가 풍부한 지역을 강조하여 성능을 향상시킵니다.
• 다섯가지 데이터셋에서 벤치마킹하는 것으로 저자가 제안하는 프레임워크가 효율적임을 증명합니다.

Method

입력 데이터는 두 이미지 쌍으로 (I_{Ref}, I_{Dis}로 구성됩니다. 학습 기반 FR-IQA의 목표는 두 이미지 사이의 매핑 함수 f(x)를 학습하여 모델의 예측 점수 \hat{y}를 MOS 점수 y에 최대한 가깝게 만드는 것입니다.

\mathbb{P} = \{x_i,y_i\}^{N_p}_{i=1}는 positive labeled 데이터를 의미하고 x_i, y_i는 각각 라벨링된 데이터와 MOS를 의미합니다. \mathbb{U} = \{x_j\}^{N_u}_{j=1}는 unlabeled 데이터를 의미하고 x_i는 MOS 라벨이 없는 unlabeled 데이터를 의미합니다. JSPL은 SSL과 PUL을 통합한 프레임워크로 FR-IQA 모델 f(x)뿐만 아니라 unlabeled 데이터가 positive인지, negative인지 구분하는 이진 분류기h(x_j)도 학습합니다.

PUL loss

h(x) 학습을 위해 저자는 \mathbb{P}는 모두 긍정으로 학습하고, \mathbb{U}는 모두 unlabeled로 간주합니다.

positive sample에 대해서는 CE loss를 사용합니다.

CE(h(x_i)) = -\mathrm{log}h(x_i).

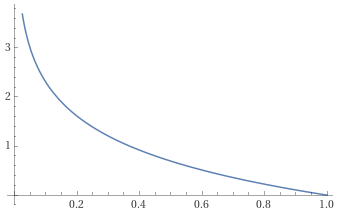
위 함수는 -\mathrm{log}(x)함수입니다. 위 함수에서 알 수 있듯이 CE loss는 positive sample에 대한 이진 분류기의 값이 1에 가까워지도록 유도하는 loss입니다.

unlabeld 데이터의 경우 positive 혹은 negative로 분류되어야 하기에 h(x)의 값이 1혹은 0에 가까워야합니다. 따라서 저자는 Entropy Loss를 사용합니다.

H(h(x_j)) = -h(x_j)\mathrm{log}h(x_j) - (1-h(x_j))\mathrm{log}(1-h(x_j)).

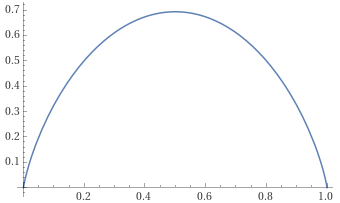
위 함수는 -xlog(x)-(1-x)log(1-x)함수입니다. 즉, Entropy loss는 이진 분류기의 값이 0 또는 1에 가까워지도록 유도하는 loss입니다.

추가로 저자는 모든 이진 분류기의 결과가 단순히 1 즉, positive sample이라고 예측하는 것을 방지하기 위해서 Negative-Enforcing(NE) loss를 추가합니다.

NE(B_u) = -log(1 - \mathrm{min}_{x_j \in B_u} h(x_j)).

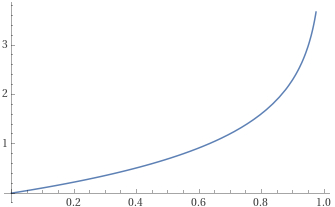
위 함수는 -\mathrm{log}(1-x)함수입니다. 즉, 배치 내에 이진 분류기의 예측 값이 제일 작은 하나의 값은 무조건 0에 가까이 가도록 학습하는 것으로 이진 분류기의 모든 예측값이 1로 향하는 것을 방지합니다.

최종 PUL loss는 위의 CE loss, Entropy loss, NE loss를 합하여 학습합니다.

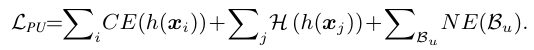
SSL loss

FR-IQA는 결국 MOS를 예측하는 회귀 task입니다. 따라서 저자는 positive sample에 대해서는 mean suared error (MSE) loss를 사용합니다.

l(f(x_i),y_i) = ||f(x_i) - y_i||^2

unlabeled 데이터의 경우 이진 분류기의 예측 값을 thresholing하여 positive로 구분되는 positive unlabeled 데이터에 대하여 마찬가지로 MSE loss를 적용합니다. positive와 negative를 구분하는 threshold는 0.5를 사용합니다.

unlabeled 데이터의 경우 실제 MOS가 없기 때문에 pseudo labeling을 해야합니다. 이때 저자는 이동 평균을 활용합니다. 이동 평균을 구하는 이유는 이전 연구를 따른다고 되어있는데 결국 분류에서는 sharpening을 자주 사용하는 데 회귀 문제에서는 적합하지 않아 경험적으로 이동평균이 제일 좋다는 것을 실험적으로 증명합니다(sharpening이 왜 적합하지 않은지는 잘 모르겠습니다…). 아무튼 이동평균은 다음과 같은 수식으로 정의됩니다.

y^*_j(t) = \alpha \cdot y^*_j(t-1)+(1-\alpha) \cdot f^t(x_j)

이에 따른 SSL loss는 positive labeled와 positive unlabled의 MSE loss를 더해서 사용합니다.

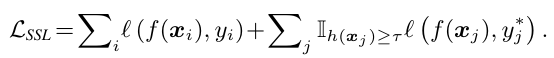
JSPL loss

최종 JSPL 프레임 워크의 loss는 다음과 같습니다.

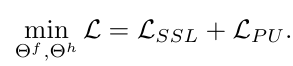
FR-IQA model

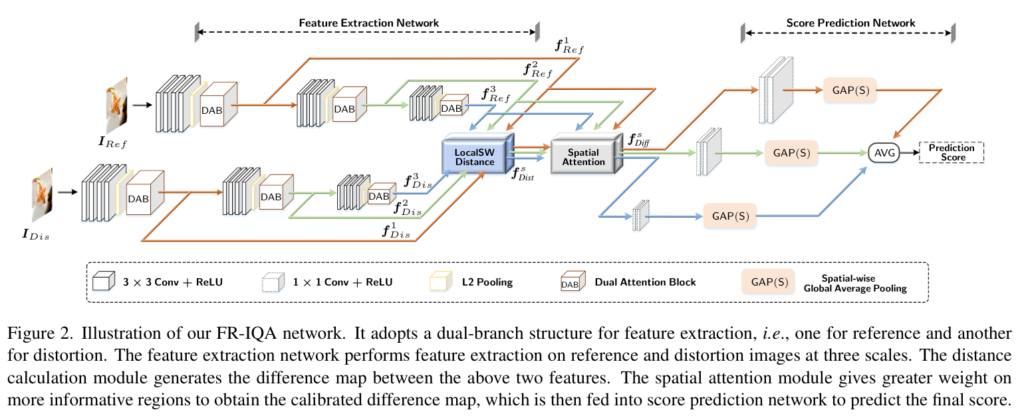
FR-IQA 모델의 구조는 Introduction에서 설명했듯이 Siamese구조를 가집니다. Siamese 구조는 샴(샴쌍둥이할때 샴) 구조로 두 pathway가 가중치를 공유하는 동일한 구조를 의미합니다. LocalSW Distance Module을 통해 원본 이미지와 왜곡된 이미지의 차이를 구하기 이전의 Feature Extraction Network의 경우 원본 이미지와 왜곡된 이미지의 feature extraction 구조의 가중치를 공유합니다. VGG16 네트워크를 기반으로하여 max pooling 대신에 L2 pooling을 사용하고 dual attention block (DAB)를 추가하여 다른 scale의 백본을 통합하여 모델의 fitting 능력을 향상시킵니다.

Local Sliced-Wasserstein(SW) Distance

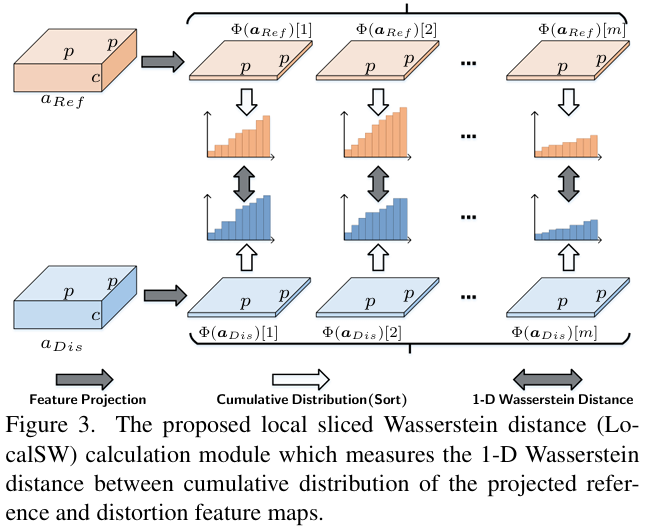
Figure 3.는 SWD의 구조를 보여줍니다. 가장 직관적인 두 이미지 간의 차이는 element-wise difference로 유클리드 거리를 구하는 것이지만 이는 GAN-based 복원의 종종 공간이 왜곡되고 원본과 정렬되지 않는 문제를 야기할 수 있다고 합니다.

따라서 저자는 SWD를 사용하는데 이미지를 겹치지 않는 p \times p로 나누어 각각의 local한 지역사이의 차이점을 구하고 각 토큰(논문에서는 slice라고 표현)을 각 채널별로 sort해 누적분포의 형태로 구성한 뒤 거리를 계산합니다.

이에 따른 distance map은 다음과 같이 정의됩니다.

f^s_{Dist} \in \mathbb{R}^{\frac{H}{p} \times \frac{W}{p} \times m}

Spatial Attention

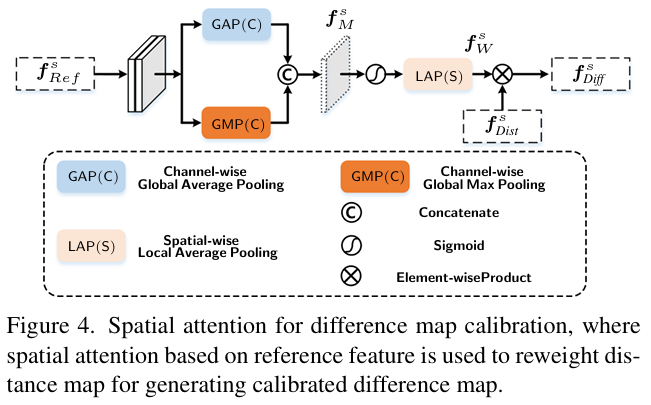
Figure 4.는 Spatial Attention의 구조를 보여줍니다. Channel-wise GAP와 Channel-wise GMP를 통해 특징을 추출한 후에 concat하고 sigmoid 함수를 통해 0~1사이로 scaling한 후에 Spatial-wise LAP를 거쳐 Local SWD를 통해 구한 Distance map과 크기를 갖도록 맞춰줍니다. 이후 element-wise 곱셈을 통해 최종 Difference map을 생성하게 됩니다.

Binary Classifier

이진 분류기의 구조는 VGG16의 첫 12 layer를 사용하고 그 뒤에 FR-IQA 모델이 사용하는 score prediction과 동일한 구조로 구성하여 분류합니다.

Experiments

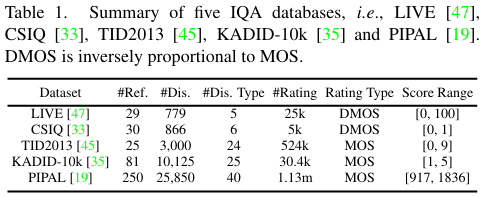
저자는 총 5개의 데이터셋에서 벤치마킹합니다. LIVE, CSIQ, TID2013, KADID-10K 그리고 PIPAL입니다. LIVE, CSIQ, TID2013 데이터셋은 상대적으로 작은 scale의 데이터셋으로 downsampling, noise, JPEG 압축 등과 같은 전통적인 왜곡 방법을 사용한 왜곡된 이미지를 사용하는 데이터셋입니다. KADID-10K 데이터셋은 추가로 denoising-restoration 과정을 거친 이미지를 왜곡된 이미지로 추가한 데이터셋으로 중간 사이즈의 데이터셋입니다. 마지막으로 PIPAL 데이터셋은 학습을 통한 FR-IQA에 가장 적합한 대규모 사이즈의 데이터셋으로 200개의 원본 이미지와 23200개의 왜곡된 이미지를 포함하는 데이터셋입니다. PIPAL 데이터셋에는 전통적인 왜곡방법, 그리고 여러가지 왜곡 방법(denoising, super-resolution, deblocking 등)을 적용한 왜곡된 이미지를 보유하고 있는 데이터셋입니다.

위 데이터는 모두 labeled 데이터입니다. 저자는 unlabeled 데이터로 세가지 방법을 적용한 데이터를 사용합니다.

1. ESRGAM: 모든 원본 이미지를 downsampling한 후에 50그룹의 ESRGAN 모델을 통해 super-resolved 이미지를 생성해 unlabeled 왜곡 이미지로 사용합니다.
2. DnCNN Synthesis: 원본 이미지에 가우시안 노이즈를 추가한 후에 50그룹의 DnCNN 모델을 사용하여 복원한 이미지를 unlabeled 왜곡 이미지로 사용합니다.
3. KADID-10k Synthesis: 저자는 25개의 degradation 기법을 랜덤하게 적용하고 복원한 이미지를 unlabeled 왜곡 이미지로 사용합니다.

평가 지표로는 SRCC와 PLCC를 사용합니다. SRCC와 PLCC에 대한 설명은 리뷰의 초반부를 참고해주시기 바랍니다.

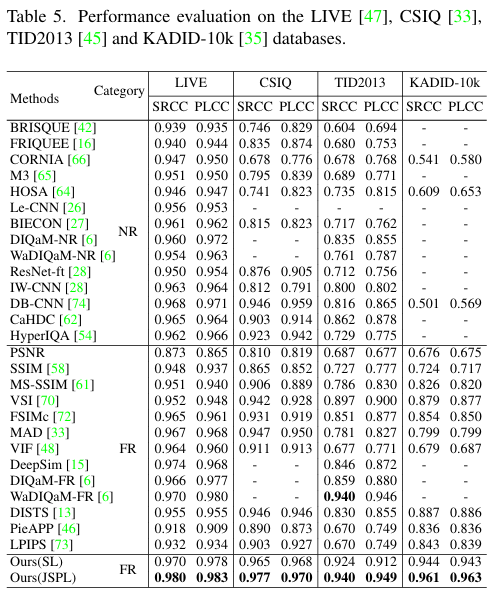
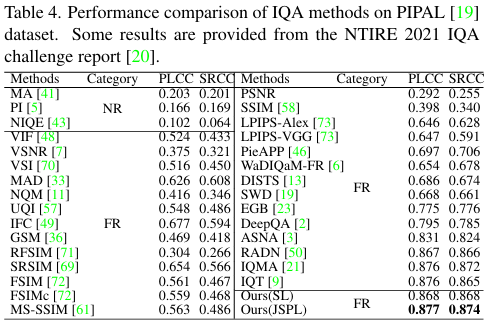
Table 5, 4는 5가지 데이터셋에서의 저자가 제안하는 방법의 성능을 보여주는 표입니다. 모든 데이터셋에서 SOTA를 달성하는 것으로 저자가 제안하는 JSPL이 효과적임을 보여주고 있습니다. 참고로 여기서 나오는 NR, FR은 non-reference/full-reference를 의미하는데 학습할 때 왜곡 이미지의 비교군인 원본 이미지의 유무를 의미합니다. PIPAL 데이터셋에서의 NR의 성능은 굉장히 처참하네요. 사실상 랜덤이 아닐까하는 수준의 성능입니다. 아무튼 모든 데이터셋에서 SOTA를 달성하는 것으로 저자가 제안하는 방법의 성능은 확실한 것 같습니다.

Ablation Study

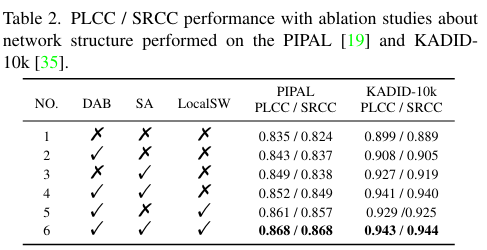
Table 2.는 각 모듈의 유무에 대한 ablation study로 LocalSW의 유무로 성능이 제일 많이 향상된 것을 확인할 수 있습니다. 확실히 유클리드 거리를 기반한 difference map보다 local feature를 잘 반영하는 SWD가 더 효율적인 것을 확인할 수 있는 대목인 것 같습니다. DAB와 SA 또한 성능 향상에 도움을 주고 있습니다.

사실 주목할만한 점은 DAB, SA, LocalSW를 모두 적용하지 않은 모델의 성능이 PIPAL 데이터셋에서는 3~4등, KADID-10k 데이터셋에서는 이미 SOTA를 달성한다는 점입니다. 모델의 구조만큼이나 JSPL 프레임워크가 성능 향상에 큰 도움을 주는 것 같습니다. 이건 사견인데 unlabeled 데이터를 추가하는 것이 학습 데이터를 늘려주는 효과가 있어 성능이 좋아진건 아닌가 싶기도 하네요. 물론 unlabeled 데이터를 잘 활용하는 것은 충분히 좋은 contribution이라고 생각합니다. 특히 KADID-10k Synthetic 데이터를 통한 unlabeled data를 추가하는 것이 어쩌면? KADID-10k 데이터셋에서의 성능에 큰 도움이 되지 않았을까 싶기도 하네요. FR-IQA task는 처음 접해서 잘은 모르지만 리뷰어들이 통과시킨 것으로 보아 치팅은 아닐 것 같습니다.

생소한 task이긴 하지만, unlabeled 데이터를 활용하는 방법은 참고할만한 것 같습니다. 또한 단순한 유클리드 거리의 한계를 보완하려는 연구가 많아지고 있는 것 같은데 SWD 방법도 참고해봐야겠습니다. 어떻게 제 연구에서 활용할 수 있을 지는 좀더 고민해봐야 겠네요 ㅎㅎ.

감사합니다.