안녕하세요. 박성준 연구원입니다. 오늘 리뷰할 논문은 ICLR2024에 게재된 논문으로 video-paragraph retrieval, cilp-caption retrieval, text-to-video retrieval 등 text와 video의 align을 맞추는 tasks들을 전반적으로 다룬 논문으로 텍스트와 비디오의 align을 더 잘 맞추는 방법에 대한 연구입니다.
논문이 복잡하고 평소에 접하지 않았던 내용들이 많이 포함되어 있어 오늘 리뷰에서는 논문을 읽기위해 필요한 사전지식에 대한 설명과 논문의 Framework를 간략하게 설명하고 다음 리뷰에서 논문에서 제안하는 방법론의 단계별 자세한 설명과 실험에 대한 내용으로 나누어 리뷰를 진행하게 되었습니다. 리뷰를 읽다가 설명이 부족하거나 내용이 이해가 안되는 부분은 댓글로 남겨주시면 아는 내용은 최대한 자세하게 설명하고, 모르는 내용은 다음 리뷰에 보완하여 설명할 수 있도록 준비하겠습니다.
Problem Definition
현존하는 많은 video-language 연구들은 long-term temporal dependencies에 집중하기 보다는 짧은 영상에 집중하는 경우가 많았습니다. 그 이유는 long-term temporal dependencies는 많은 연산을 필요로 하기 때문입니다. 적은 연산량을 유지하면서 long-term temporal dependencies를 얻는 실현 가능한 방법 중 하나는 video clips와 video captions를 활용하는 것입니다(video caption의 정보가 video의 context정보를 담고 있기 때문). 하지만, clips와 captions를 활용하는 방법은 multi-granularity noisy correspondence (MNC) 문제로 인해 좋은 성능을 보장하지 않습니다. MNC는 clip-caption misalignment (coarse-grained) 와 frame-word misalignment (fine-grained)를 의미합니다. 즉, video와 text의 align이 잘 맞지 않는다는 문제입니다. 이러한 문제는 temporal learning, video understanding을 방해하는 요소입니다.
해당 논문에서 제안하는 방법인 NOise Robust Temporal Optimal traNsport (Norton)은 Unified Optimal Transport(OT) Framework를 통해 MNC를 다룹니다. Optimal Transport (OT)를 이용한 Framework로 MNC 문제를 해결하고 long-term dependencies를 캡쳐할 수 있게 합니다. 구체적인 방법론의 내용은 다음 리뷰에서 다루기로하고, 이번 리뷰에서는 논문에서 MNC를 해결하기 위한 방법으로 사용하는 Optimal Transport에 대해 먼저 알아보겠습니다.
Optimal Transport
Optimal Transport (OT)는 두 확률 분포 간의 거리를 계산하고 이를 최소화하는 문제를 다루는 수학적 이론입니다. OT의 기본 아이디어는 두 개의 확률 분포 P와Q 사이의 최적의(Optimal) 이동(Transport) 전략을 찾는 것입니다. 인공지능의 관점에서 본다면 Diffusion, GAN과 같은 생성형 모델이 생성된 데이터의 분포와 실제 데이터의 분포를 일치시키기 위해 사용되거나, Domain Adaptation에서 다른 도메인에서 학습된 모델을 맞추기 위해 사용되는 등 여러가지 분야에서 활용되고 있습니다.
Wasserstein Distance
전통적인 OT문제는 주로 Wasserstein 거리를 활용하는데 Wasserstein 거리는 두 확률 분포 간의 거리를 측정하는 지표로, 두 분포를 가장 효율적으로 맞추기 위해 이동해야 하는 총 양을 측정합니다. Wasserstein 거리에서 사용되는 조인트 분포는 Joint Distribution으로 두 개 이상의 확률 변수 간의 결합될 확률을 설명하는 분포로 여러 확률 변수가 동시에 특정 값을 가질 확률을 나타냅니다. 즉, 두 확률 분포 간의 연결 계획을 나타내는 요소입니다.
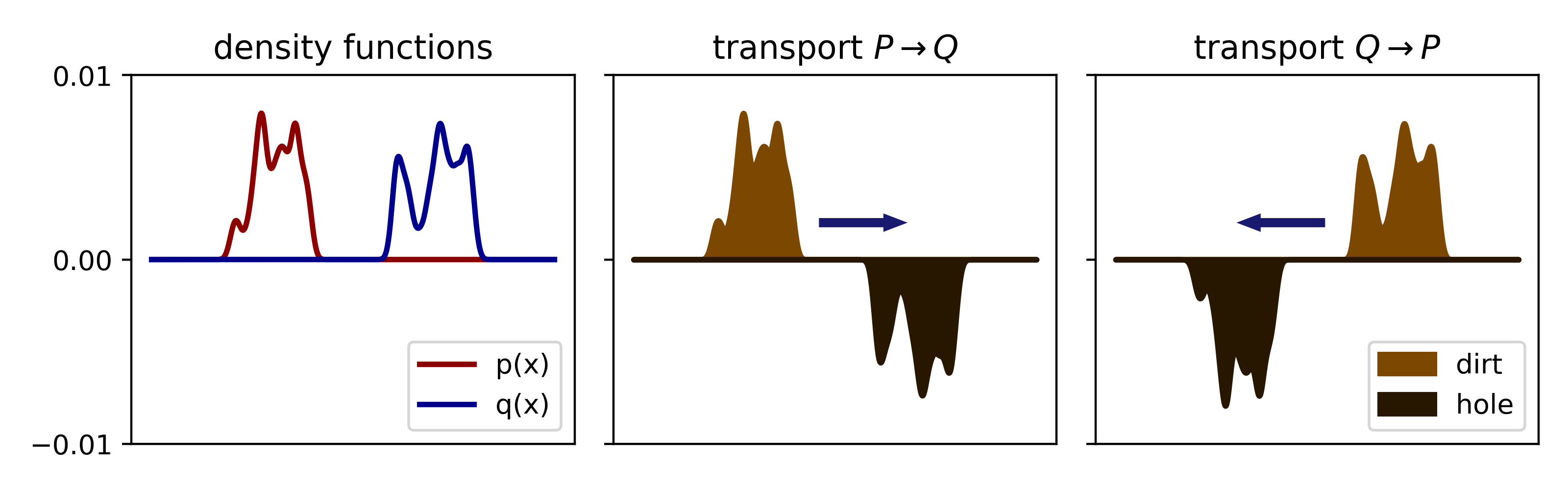
위의 그림를 예시로 Optimal Transport는 확률 분포 p(x)와 q(x)가 존재할 때, 확률 분포를 p에서 q로, q에서 p로 이동시키는 최적의 전략에 대한 연구를 의미합니다.
W_p(P, Q) = \left( \inf_{\gamma \in \Pi(P, Q)} \int |x - y|^p \, d\gamma(x, y) \right)^{1/p}
수식은 다음과 같습니다. 여기서 |x-y|는 두 지점 사이의 거리로 p는 일반적으로 1이나 2로 설정됩니다. d(x,y)는 distance(x, y)로 유클리드 거리 혹은 다른 거리 메트릭일 수 있습니다. \int |x - y|^p \, d\gamma(x, y) 는 \gamma를 따라 x에서 y로 이동할 때의 전체 비용을 나타냅니다.
\Pi(P,Q)는 P와 Q를 연결하는 모든 가능한 조인트 분포의 집합입니다. \gamma는 \Pi(P,Q)에서 두 분포를 연결하는 특정한 조인트 분포로 두 분포 사이의 이동 계획을 나타냅니다. 즉, 두 확률 분포 P와 Q를 연결하는 가능한 모든 확률적 연결을 나타냅니다. 예를 들어 두개의 확률 변수 X와 Y가 있다고 할 때, 이들의 조인트 확률 분포는 P(X = x, Y = y)로 나타낼 수 있고, 이는 X가 특정 값 x를 갖고, 동시에 Y가 y를 가질 확률을 의미합니다.
결국 Wasserstein 거리 계산에서의 목표는 두 분포 P와 Q 사이의 모든 가능한 조인트 분포 \gamma 중에서 비용을 최소화하는 최적의 조인트 분포를 찾는 것입니다. 더 직관적으로는 분포 P에서 분포 Q로의 최적의 이동 경로를 찾는다를 의미합니다.
이러한 Wasserstein 거리는 두 확률 분포 안의 확률 변수의 매칭(이동계획)도 고려하기에 전체적인 구조적인 차이를 고려할 수 있습니다. 즉, 단순히 두 분포의 평균, 분산을 고려하는 것이 아니라 두 분포의 생김새를 반영합니다. 따라서 Euclidean 거리나 Kullback-Leibler (KL) Divergence와 같은 다른 거리 측정법와 차이점이 있습니다. 또한, Wasserstein 거리는 두 분포가 근접해질수록 거리 값이 매끄럽게 변할뿐만 아니라 이상치에 민감하지도 않기에 인공지능 학습의 관점에서 최적화시킬때 장점이 있습니다. KL-Divergence의 경우, 두 분포가 겹치지 않을 경우 말그대로 발산할 수 있는 반면, Wasserstein 거리는 분포 사이의 모든 가능한 매핑을 고려하기에 더 Robust하다는 장점도 있습니다.
위에서 설명한 Wasserstein 거리는 다양한 데이터 유형과 상황에서 보다 안정적이고 직관적인 분포 간의 비교를 가능하게 하며, 특히 분포의 구조적 차이를 정확하게 반영하는 데 강점이 있습니다.
일반적으로 Wasserstein 거리는 연속적인 분포에 대해 정의된 개념으로 \gamma가 두 분포 간의 최적의 결합 분포를 찾는 데 초점을 둡니다. 이러한 방식은 계산 비용이 높아 고차원 문제에서 계산이 복잡해지고, 효율적인 근사방법이 필요합니다.
OT in discrete manner
OT는 이산적인 확률 분포를 갖는 데이터에 대해서는 선형 계획 형태로 쉽게 표현할 수 있습니다. 비용 행렬 C와 이동 계획 행렬 \pi를 통해 표현되며 이산적 점들 사이의 매핑을 행렬을 통해 나타냅니다.
각각 길이가 n과 m인 두 확률 벡터 \mu와 \nu 사이의 비용 행렬 C (크기 n*m)이 주어지면 비용을 최소화하는 이동 계획 \pi를 찾는 것을 통해 OT문제를 다룹니다.
\min_{\pi \in U(\mu, \nu)} \sum_{i=1}^{n} \sum_{j=1}^{m} \pi_{ij} C_{ij}
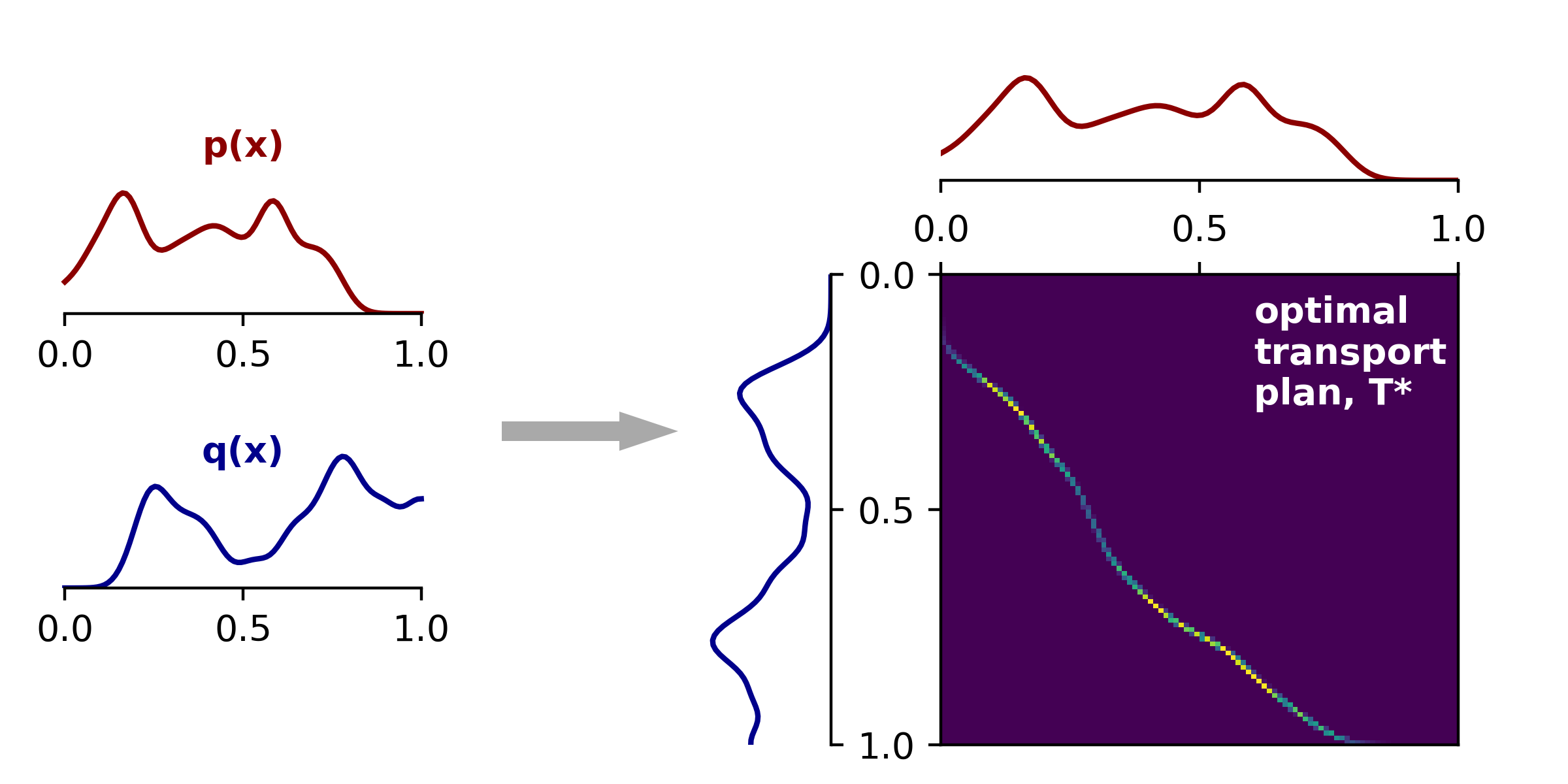
이해를 위해 그림으로 1차원 확률 분포를 예시로 확률 분포 p(x)를 q(x)로 이동시키는 최적의 이동전략을 구하기 위해 우측의 그림과 같이 p(x) 내 확률 변수와 q(x) 내 확률 변수를 매핑시키고, 어떻게 이동시키는 것이 제일 최적인지를 구하는 것입니다. 위 그림은 연속적인 확률분포를 다루는 문제로 Wasserstein 거리의 예시이지만, 선형 계획 형태의 OT 또한 위와 같은 방식으로 OT문제를 다룹니다(Wasserstein 거리, 이산 계획 형태의 OT 모두 본질은 같음). 이산 계획 형태의 OT는 위 그림에서 데이터가 벡터로, 오른쪽 매핑 과정이 행렬을 통해 진행됩니다.
Wasserstein 거리에 비해 더 직관적이고 계산하기 쉬울 뿐만 아니라 행렬의 곱과 합을 통해 해결되고 인공지능에서 다루는 데이터는 이산 분포의 벡터들로 표현되기에 인공지능에서 활용되는 OT문제는 대부분 위의 수식의 형태를 가진다고 생각하시면 될 것 같습니다. 해당 논문에서도 위의 선형 계획 형태의 OT를 다루고 있습니다.
정리하면, Wasserstein 거리와 선형 계획 형태의 OT문제는 본직적으로 같은 목표를 갖고 있지만(두 확률 분포 사이의 거리를 최소화하는 것), 다루는 데이터의 형태와 접근 방식에서 차이가 있으며 인공지능에서는 이산적인 데이터를 다루고 행렬 연산이 유리한 선형 계획 형태의 OT를 주로 사용합니다.
Sinkhorn Algorithm
Sinkhorn 알고리즘은 OT 문제의 계산을 효율적으로 다루기 위한 알고리즘으로 OT문제에 엔트로피 항을 추가한 형태입니다.
\min_{\pi \in U(\mu, \nu)} \sum_{i=1}^{n} \sum_{j=1}^{m} \pi_{ij} C_{ij} + \epsilon \sum_{i=1}^{n} \sum_{j=1}^{m} \pi_{ij} \log(\pi_{ij})
\epsilon>0은 정규화 강도를 조절하는 파라미터로 값이 커질수록 문제는 부드럽게되고 작을수록 원래의 OT 문제와 가까워집니다. 위 수식에서의 두번째 항이 엔트로피 항으로 \pi 행렬의 분포를 균일하게 만들어주는 효과를 줍니다.
Sinkhorn 알고리즘은 다음과 같은 과정 반복하는 것으로 최적의 \pi를 찾습니다.
- 초기화: 초기 이동 계획 \pi를 설정합니다.
- 행과 열 스케일링:
- 행 스케일링: \pi의 각 행의 합이 \mu에 맞도록 조정합니다.
- 열 스케일링: \pi의 각 열의 합이 \nu에 맞도록 조정합니다.
- 반복: 위의 스케일링 과정을 \pi가 수렴할 때까지 반복합니다.
Sinkhorn 알고리즘은 이처럼 엔트로피 정규화를 도입하여 OT 문제를 더 빠르게 풀 수 있는 알고리즘으로 이산 계획 형태의 OT문제와 결합하여 대규모 데이터에서도 효율적으로 사용할 수 있도록 도와줍니다.
Introduction

다시 논문으로 돌아와 저자는 크게 MNC 문제를 두 granularites로 구분하여 설명합니다.
- Coarse-grained misalignment (Clip-caption).
- Fine-grained misalignment(Frame-word).
첫번째, Coarse-grained misalignment에는 두 가지 misalignment가 존재합니다. asynchronous와 irrelevant misalignment입니다. asynchronous는 subtitles(captions or 자막)와 visual clips간의 temporal misalignment를 의미합니다. Figure 1.에서 t_1에 해당합니다. t_1의 caption정보가 영상 내 다른 clip의 설명에 해당에 시간적으로 일치하지 않아 asynchronous misalignment에 해당하는 coarse-grained misalignment입니다. irrelevant misalignment는 말 그대로 잘못된 경우로 어느 video clip과도 맞지 않는 caption을 뜻합니다. 어느 video clip과도 align되지 않기에 irrelevant misalignment입니다. Figure 1.에서 t_2와 t_6이 irrelevant misalignment에 해당됩니다. 저자는 비디오와 비디오를 설명하는 캡션이 있는 HowTo100M 데이터셋에서 30%의 clip-caption쌍만이 시각적으로 잘 align되어 있으면 그 중에서도 자연스럽게 잘 align된 것은 15%밖에 되지 않는다고 말하며 기존 연구들이 이러한 misalignment에 무관심했었다는 것을 지적합니다.
두번째, Fine-grained misalignment는 video clip과 설명하는 문장이 부분적으로만 상관관계가 존재하는 경우로, Figure 1.에서 t_5가 이에 해당합니다. “sugar goes on top”은 v_5와 강한 상관관계를 가지지만, “watch the glaze take off”는 상관 관계가 없음을 지적하며 이러한 무관한 단어 혹은 프레임은 단어의 식별을 왜곡하는 것으로 더 나아가 부정확한 유사성 측정을 초래하는 문제라고 저자는 주장합니다.
저자는 기존의 연구 중 소수만이 Coarse-grained misalignment를 문제 삼았으며, Fine-grained misalignment를 문제 삼은 연구는 아직 없었다는 것을 강조하며 MNC는 temporal modeling에 있어 중요한 장애물임을 언급합니다. 저자가 제안하는 Norton은 OT기반의 Framework를 사용하는 것으로 시간적 상관관계를 파악합니다.
video-paragraph contrast를 위해 Norton은 fine-to-coarse 관점에서 video clip과 caption 사이의 sequence 거리를 측정합니다. fine-trained misalignment를 다루기 위하여 Norton은 clip-caption 쌍에서 중요한 단어와 핵심 프레임을 구분하기 위하여 token-wise soft-maximum 연산을 사용합니다. 이 연산자는 fine-grained multi-modal interaction에서 clip-caption의 유사성을 측정하는 방식을 개선할 수 있습니다. 개선된 유사성을 기반으로 Norton은 clip과 caption 사이의 유연한 할당이 가능하고 OT를 활용하여 video clip을 여러개의 관련있는 captions에 재정렬하고 caption또한 관련있는 여러개의 video clips에 재정렬하는 것으로 asynchronous misalignment를 완화합니다. irrelevant misalignment를 위해서는 noisy한 clip이나 caption에 대한 후보 alignable target으로 기능하는 alignable prompt bucket을 통해 해결합니다. 특정 bucket에 align된 것들을 버리는 것으로 OT과정 중에 필요 없는 콘텐츠를 걸러내 long video에 대한 OT의 계산 비용을 줄입니다.
clip-caption contrast에서 Norton은 faulty negative problem을 지적합니다. 구체적으로 설명하면 올바르게 매칭된 clip-caption 쌍을 제외한 유사한 의미를 는 clip과 caption은 contrastive learning에서 negative로 간주되어 학습되는 데 이는 clip-wise representation에 악영향을 미칩니다. Norton은 batch 내 clip-caption 쌍을 추가적인 supervision을 통해 contrastive loss에 활용하는 것으로 잠재적으로 faulty negative sample이 생길 가능성을 낮추고 temporal learning의 성능을 올립니다.
이에 따른 Norton의 main contribution은 다음과 같습니다.
- 저자는 temporal learning(video-language 연구)에서의 coarse-grained asynchronous misalignment, coarse-grained irrelevant misalignment 그리고 fine-grained misalignment 문제를 포함하는 multi-granularity noisy correspondence (MNC)문제를 정의합니다.
- MNC문제의 해결을 위해 soft-maximum 연산자, alignable prompt bucket, faulty negative exploitation을 활용하는 OT기반 프레임워크를 통해 효과적이고 robust한 correspondence learning 방법 NOise Robust Temporal Optimal traNsport (Norton)을 제안합니다. video retrieval, videoQA 등의 task에서의 실험결과를 통해 Norton의 강력함을 증명합니다.
Method

위 Figure가 Norton의 Framework을 보여주는 Figure입니다. 저자가 제안하는 multi-granularity correspondence 학습은 총 3단계로 진행됩니다.
1단계: Fine-grained Alignment
clip과 caption 사이의 fine-grained 유사도를 측정하는 단계로 video clip과 text caption 단어 사이의 유사도를 계산하여 frame-word 유사도 행렬을 생성합니다. 그후 각 행과 열에 대해 log-sum-exp (로그-합-지수) 연산자를 적용하여 더 정확한 fine-grained 유사도를 얻습니다.
2단계: Coarse-grained Alignment
clip들과 caption들 간의 coarse한 align을 수행하는 단계로 clip-caption 유사도 행렬에 alignable prompt bucket를 추가하여 관련 없는 clip이나 caption을 필터링합니다. 필터링틀 통해 각 clip, 혹은 caption에 관련없는 요소를 제거하는 것으로 좀 더 정확한 유사도 행렬을 얻을 수 있습니다.
3단계: Video-paragraph Contrastive Learning
video와 paragraph 사이의 시간적 상관관계를 coarse한 level에서 align하고 위에서 설명한 OT(선형 계획 형태의 OT와 Sinkhorn 알고리즘)을 활용해 유사도를 계산합니다. clip-caption 유사도 행렬에 Sinkhorn 알고리즘을 반복 적용하여 asynchronous misalignment를 해결하고 최적인 이동 거리를 계산합니다. 최적 이동거리(OT)를 활용하여 coarse한 video-paragraph 유사도를 얻을 수 있습니다.
즉, Norton은 fine-grained level에서 시작하여 coarse-grained level까지 align하는 방법으로 각 단계마다 점점 더 높은 수준의 유사도를 포착하여 최종적으로 paragraph와 video간의 정확한 관계를 얻어 기존 방법론들이 다루지 못했던 long-term temporal dependencies또한 얻을 수 있게 됩니다. fine-to-coarse 관점에서 다단계로 유사도를 계산하고 최적의 매핑방식을 구하는 과정을 통해 비디오의 각 클립이 어떠한 단어 혹은 문장에 연관이 있는지부터 영상이 어떤 문단에 시각적(visual)으로 시간적(temporal)으로 연결되어 있는지를 align할 수 있습니다.
저자가 제안하는 Norton은 위와 같은 총 3단계를 통해 multi-granurality correspondence 학습을 진행합니다.
요약하면 기존 video-language 연구는 높은 연산량으로 인해 long-term temporal dependencies를 고려하지 않는 경우가 많았습니다.
낮은 연산량으로 long-term temporal dependencies를 고려하기 위한 방법으로 video caption을 활용할 수 있으나 fine-grained, coarse-grained level에서 captions가 video에 잘 align되지 않는 multi-granularity noisy correspondence (MNC) 문제가 존재하여 제대로 temporal 정보를 파악하는 데에 한계가 있었습니다.
따라서 저자는 MNC 문제를 해결하고 long-term temporal dependencies를 잘 파악하고자 Optimal Transport(OT)를 활용하였습니다.
OT는 두 확률 분포 사이의 거리를 파악하고 최적의 이동 경로를 구하는 이론으로 기존 euclidean 거리 혹은 KL-divergence보다 정확하고 효율적으로 두 확률 분포(video, text)의 거리를 파악하고 매핑할 수 있습니다.
OT를 활용한 저자가 제안하는 NOise Robust Temporal Optimal traNsport (Norton)은 fine-to-coarse 과정을 통해 효과적으로 frame-word, clip-caption, video-paragraph를 align할 수 있습니다.
오늘 리뷰는 여기서 마치고 다음 리뷰에서는 Norton의 단계별 방법론의 자세한 설명과 실험 결과에 대한 내용으로 돌아오겠습니다.
감사합니다.
안녕하세요 성준님 리뷰 감사합니다
작성해주신 리뷰가 다룬 문제에서 연구들이 misalignment 를 정의하는 방법에 대해 질문이 있어 댓글을 남깁니다. 소개해주신 논문에서 “HowTo100M 데이터셋에서 30%의 clip-caption쌍만이 시각적으로 잘 align되어 있으면 그 중에서도 자연스럽게 잘 align된 것은 15%밖에 되지 않는다고” 라고 함을 소개해주셨는데, align 여부에 대한 판독은 주관적 판단에 영향을 받을 것 같습니다. 이러한 주관적 요소(align의 정도)를 평가하는 방법은 따로 없는지 궁금합니다.
제가 이해한 바가 맞다면, 해당 연구는 데이터와 캡션의 misalignment를 데이터셋의 내제적 문제로서 재라벨링 등이 아닌 학습과정에서의 해결법을 제시한 것 같습니다. 혹시 LLM 등을 활용해 데이터를 재라벨링해 사용하는 방법과 해당 학습개선 방법을 결합, 비교한 연구도 진행되고 있나요? 있다면 두 방법중 어느 방법이 성능 개선에 더 효과적일지 궁금하네요 ㅎㅎ
감사합니다!
안녕하세요 유진님 좋은 댓글 감사합니다.
유진님이 지적해주신 것처럼 저자가 데이터셋에서 30%만이 align이 잘 되어있다고 지적하는 부분은 주관적 판단이 섞일 수 밖에 없다고 생각합니다. 저자는 CVPR 2022에 게재된 Temporal Alignment Networks for Long-term Video 논문의 분석을 인용해 30%만이 잘 align되어 있음을 소개합니다. 해당 논문에서는 video에 해당하는 caption이 시각적으로 video에 들어나지 않는 문장들도 포함되어 있다는 것을 언급하며 30%만이 align이 잘 되어있음을 지적하는데 아쉽게도 이 논문에서도 align이 잘 되어있는 지에 대한 정량적 기준을 소개하지 않아 아무래도 학계에서 사용되는 caption의 주관적 요소를 평가하는 방법은 존재하지 않는 것 같습니다. LLM을 사용해 caption의 정확도를 올리려는 연구 또한 진행되고 있습니다. 하지만, video-language level에서 LLM을 활용한 재라벨링을 통한 align을 맞추는 방법이 아니라 downstream task에서 prompt를 활용해 caption을 잘 활용하려는 연구들이라 정확한 비교는 어려울 것 같습니다.
감사합니다.
안녕하세요. 좋은 리뷰 감사합니다.
해당 연구 분야에 굉장히 흥미가 드네요.
논문에서 misalignment에 대해서 구체적으로 분류하고 이것이 문제가 있음을 어필한 점이 굉장히 contribution이 있는 것 같습니다. 그런데 읽다보면 아예 잘못된 caption이 있는가 하면, 어떤 caption은 텍스트의 일부분만 프레임과 상관관계가 있고 나머지 부분은 상관 관계가 없다고 하는데,,,, 이런 전개로 논문이 시작된다면 새롭게 데이터셋을 어필해야할 것 같은데 실험 결과가 없으니 아직 이 방법론이 효과가 있는지는 모르겠으나(물론 효과가 있었으니 엑셉되었다고 생각합니다) 논문의 저자가 따로 데이터셋 구축에 대해서는 언급하지 않았나요…?
감사합니다.
안녕하세요 주연님 좋은 댓글 감사합니다.
저자가 따로 데이터셋을 구축을 언급하지는 않습니다. 저자가 제안하는 방법이 기존 contrastive learning에서의 cosine 유사도는 temporal misalignment를 고려하지 않아 video-language alignment를 맞추는데 어려움이 있음을 지적하고 Optimal Transport를 통해 정렬하는 데에 있어 그런 것으로 생각됩니다.
감사합니다.
안녕하세요 성준님 좋은 리뷰 감사합니다.
본문의 Method ‘2단계: Coarse-grained Alignment’에서 질문이 있습니다. 설명에 따르면 ‘clip-caption 유사도 행렬에 alignable prompt bucket를 추가하여 관련 없는 clip이나 caption을 필터링’한다고 했는데 이는 caption 전체가 필터링 되는건가요 아니면 caption안의 단어가 필터링 되는건가요?
감사합니다.
안녕하세요 의철님 좋은 댓글 감사합니다.
alignable prompt bucket은 캡션 전체를 필터링합니다. video-caption 쌍이 잘 align되지 않을 때 이런 쌍을 사용하지 않는 것으로 올바른 쌍만을 사용해 학습하는 것으로 저자는 학습에 방해가 되지 않도록 유도하는 방법입니다.
감사합니다.