지난번 리뷰에 이어 이번 논문 리뷰도 Adapter 관련 논문입니다. CVPR2023에 게재된 논문으로 지난번 ViT Adapter랑은 접근 방식이 제법 다른 방법론입니다.
Intro
InternImage, GPT 등등 Vision, NLP 분야 내 대부분의 foundation 모델들은 방대한 자원을 가지고 학습을 수행하여 우수한 성능을 달성하지만, 이러한 대용량 데이터 기반 학습 방식은 많은 학교나 기관에서 시도하기 어려운 방법입니다.
대용량 데이터를 취득하는 것은 어려울뿐더러, 설령 공개된 대용량 데이터가 존재한다 하더라도, 거대 모델을 대용량 데이터로 학습시키기 위해서는 상당히 많은 양의 GPU 자원이 필요로 하기 때문이겠죠.
그렇다면 이미 대용량 데이터로 사전 학습된 foundation model을 가져다가 저희가 풀고자 하는 downstream task에 fine-tuning을 하는 방향으로 접근하면 어떨까요? 아쉽지만 이러한 방향 역시도 쉽지만은 않습니다. 이전 연구들에서는 사전학습된 거대 모델을 fine-tuning 할 때 적은 자원을 활용할 경우 모델의 특징 표현력이 감소된다는 결과를 발표했습니다. 아무래도 fine-tuning을 수행하기 위한 데이터 셋의 규모가 작으면 방대한 양의 가중치들이 해당 학습 셋으로 fitting이 되지 않았나 싶습니다.
설령 적절한 양의 데이터를 가지고 있어 사전 학습된 모델 전체 파라미터에 대해 fine-tuning을 하여 성능을 잘 뽑아낼 수 있다고 할지라도, 모델 학습에 사용되는 파라미터가 너무 많아 GPU 리소스가 과하게 필요한 것 역시 foundation model을 fine-tuning하는데 어려움으로 남게 됩니다.
다시 말해, Pretraining & Fine-tuning이라는 저희가 학부 인공지능 수업에서부터 배웠던 매우 직관적인 패러다임은 이러한 foundation model에 한해서는 함부로 활용하기 어렵다는 것이죠.
이러한 문제를 해결하기 위해, NLP 분야에서는 Adapter나 Prompt Tuning을 통하여 사전학습된 파라미터들은 고정시켜놓고, 기존 백본보다 10% 이하에 작은 파라미터들로 구성된 레이어들을 학습시키는 방식을 활용하였다고 합니다.
Prompt Tuning이란 새로운 task에 따른 입력 공간을 변화시키기 위해 입력 혹은 중간 레이어들에 학습 가능한 파라미터를 추가하는 과정을 의미합니다. Adapter tuning의 경우 새로운 task 수행을 위해 사전 학습된 모델을 구성하는 각 블록들 사이에 학습 가능한 bottleneck 구조를 추가하는 것을 의미한다고 합니다.
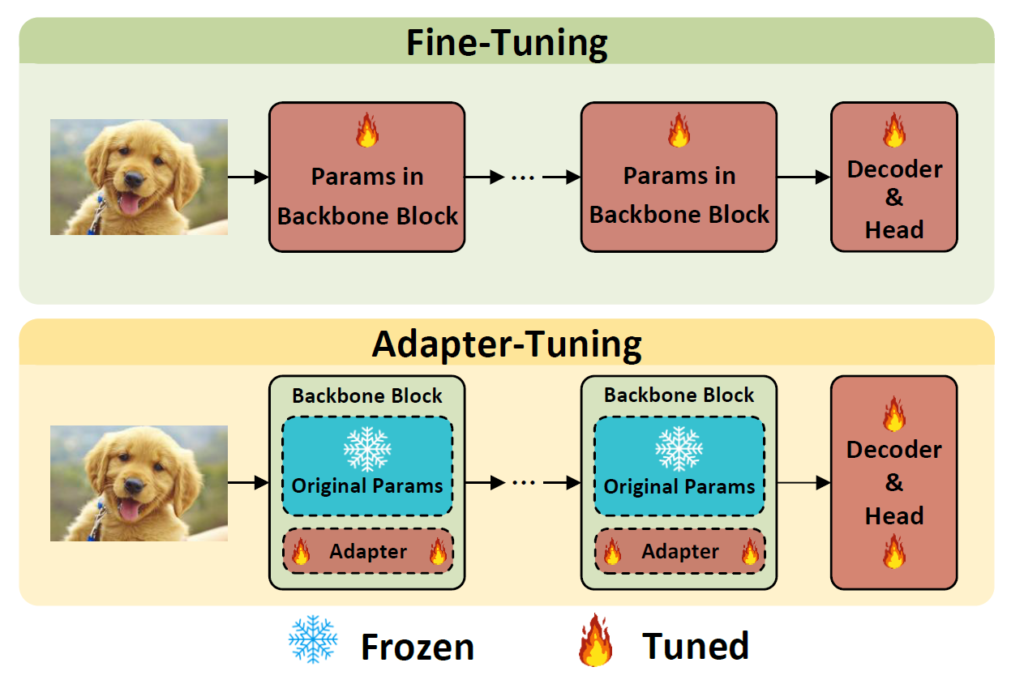
그림 1에서 보이듯이 Fine-tuning이 모델 전체를 다 학습시키는 것이라면, Adapter-Tuning 방식은 사전학습된 파라미터들은 내버려두고, 전체 모델 파라미터의 10% 미만 수준의 task-specific 블록을 추가하여 해당 블록들을 학습시킨다고 보시면 될 것 같네요.
아무튼 프롬포트 튜닝 또는 어댑터 튜닝 방식이 NLP에서 좋은 결과를 보여주었으며, Vision 도메인에서도 이러한 튜닝 방식을 적극 도입했다고 합니다. 가장 대표적인 것이 Visual Prompt Tuning (VPT)라는 것인데, 저자들은 VPT 방법론이 영상 분류에서는 좋은 성능을 보여주었지만, segmentation과 같은 dense-prediction task에서는 좋은 성능을 보여주지 못하였다고 합니다.
따라서 저자들은 Visual Dense Prediction task를 위한 Adapter tuning 기법을 새롭게 제안하고 싶어했고, ImageNet-22K으로 사전 학습된 Swin Transformer를 기본 백본으로 기존 adapter 방법들을 실험하였다고 합니다. 가장 대표적으로 bottleneck adapter 구조를 Swin block 사이 사이에 추가한 뒤, Swin block들은 모두 freeze 시키고 adapter들만 학습시켰는데, 이러한 방식으로는 VPT 논문에서 언급된 fine-tuning 방식 성능과 비교하여 좋지 못한 성능을 달성했다고 합니다.
저자들은 다양한 실험들을 수행하고 결과적으로 가벼운 adapter 구조가 가장 효과적이라고 주장하게 되는데, 바로 Low-Rank Adapter (LoRAND)라는 새로운 adapter 구조를 제안합니다.
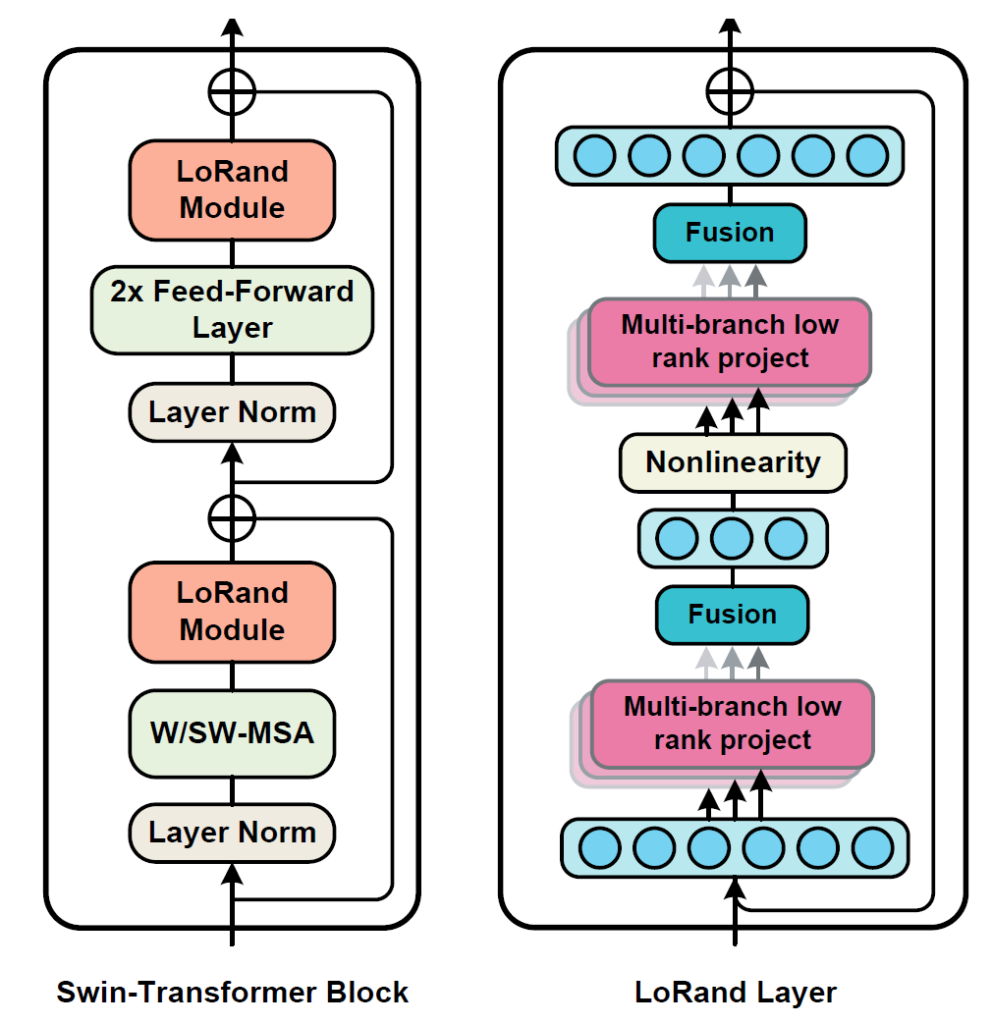
LoRand layer의 역할은 adapter의 파라미터 수를 감소시키는 것으로, FC layer의 투영 행렬이 LoRAND에는 존재하여 해당 행렬이 low-rank 행렬들과 내적하면서 FC 레이어의 파라미터수를 80% 이상 감소시킨다고 합니다. 보다 자세한 설명은 바로 밑에서 다뤄보도록 하겠습니다.
Low-rank Approximation
LoRand layer의 핵심은 Low Rank approximation이기 때문에 Low-rank approximation에 대해서 먼저 간단하게 알아보겠습니다. Low-rank approximation이란 쉽게 말하면 여러개의 저차원 행렬(또는 텐서)를 사용해서 더 큰 차원의 행렬(또는 텐서)를 근사화하는 것을 의미합니다.
사실 개념이 SVD 같이 Matrix Decomposition이랑 많이 유사해보이는데, 만약 b x c 크기의 행렬 M이 있다고 했을 때, 해당 행렬을 N개의 low-rank 행렬들의 집합 Q로 근사화 할 수 있게 됩니다.
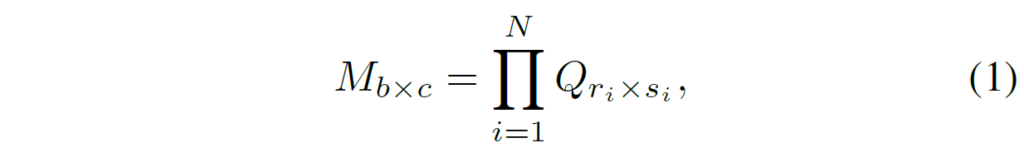
여기서 low-rank의 개수 N은 어떠한 근사화 기법을 사용하는지에 따라 달라지게 되는데, 본 논문에서는 휴리스틱한 학습 방식을 통해 adapter의 행렬들을 low-rank approximation 했다고 합니다. 대충 뭐 SVD 처럼 행렬 3개 기준으로 분리한 뒤 학습시켰다는 의미인 것 같은데 밑에서 LoRand 구현에 대해 다룰 때 조금 더 다루겠습니다.
Adapter Tuning Paradigm
우선 Adapter를 어떻게 tuning하는지에 대해서 간략하게 설명하겠습니다. 어떠한 데이터 셋 D = \{(x_{i}, y_{i})\}^{N}_{i=1} 에 대하여 추론 결과와 label 간에 loss 계산은 다음과 같이 진행한다고 볼 수 있습니다.
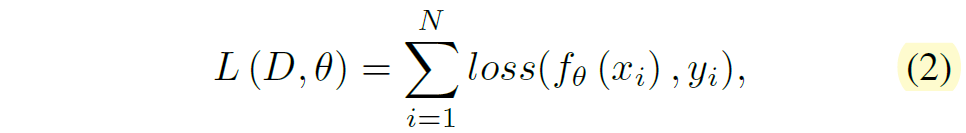
여기서 f_{\theta} 는 network의 forward function을, loss는 loss function을 의미합니다. 말 그대로 입력을 모델에 forwarding 시켜서 나온 결과와 label y간에 loss를 계산한다~라는 supervised learning 방식을 아주 직관적이게 수식으로 나타낸 것입니다.
수식2를 통해 loss를 계산하게 되면 이제는 역전파 과정을 통해 learnable parameters \theta 가 최적화됩니다.
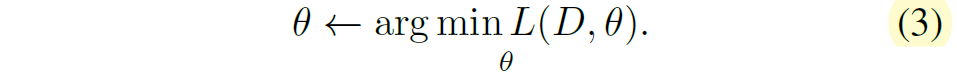
수식 2~3번까지가 일반적인 모델의 학습 과정이었다면 이제는 adapter tuning 관점에서 수식 2, 3을 다시 조정하력 ㅗ합니다. 우선 adapter tuning에서는 사전학습된 원래의 모델의 파라미터 \theta 와 adapter의 파라미터 \theta_{A} 로 구분을 지을 수 있습니다.
그리고 원래 모델의 파라미터 \theta 에 대해서도 freeze한 부분과 학습 가능하도록 바꾼 부분으로 나누어 \theta = \{ \theta_{F}, \theta_{T} \} 로 구분을 지을 수 있습니다. 그러면 여기서 학습 가능한 파라미터들만 모두 모으면 \Omega = \{ \theta_{A}, \theta_{T} \} 로 나타낼 수 있습니다. 이러한 용어 정리를 기반으로 수식2, 3을 바꿔쓰면 adapter tuning 과정은 다음과 같이 나타낼 수 있습니다.
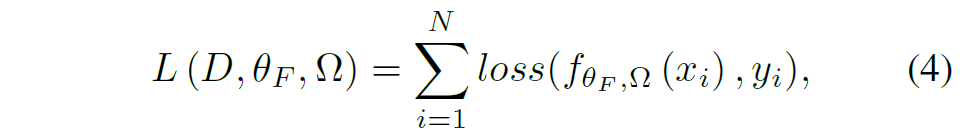
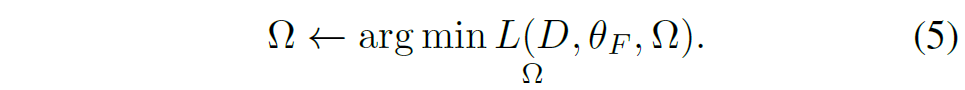
LoRand
그럼 이제 Adapter의 구조에 대해서 살펴볼까요? NLP에서 많이 사용하는 일반적인 Adapter의 경우 병목 구조를 많이들 사용하는데 병목 구조는 아래와 같이 구성되어 있습니다.
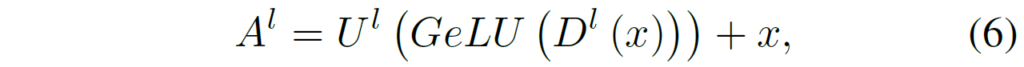
여기서 U와 D는 up/down projection layer를 의미하며, GeLU는 activation function을 나타내죠. 즉 adapter의 구조는 어떠한 feature x에 대해 down projection을 수행하는 fc layer와, 비선형 활성화 함수, 그리고 다시 원래의 차원으로 올려주는 up projection layer로 크게 구성이 되며 그 다음에 residual connection 연산을 수행하는 매우 단순한 구조입니다.
여기서 이 Projection layer는 FC layer로 구성되기 때문에 아래 수식 7과 같이 weight와 bias 꼴로 나타낼 수 있으며, low-rank approximation에서는 bias보다는 Weight가 더 중요한 파라미터라는 것을 염두하셔야 합니다.
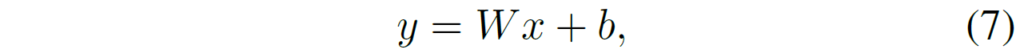
자 그러면 이러한 adapter의 학습 파라미터의 수를 줄이기 위해서, 저자들은 low-rank approximation을 기반으로 구성된 adapter 즉 LoRand라는 새로운 구조를 제안하게 되는데요.
인트로에서의 그림 2에서 LoRand Layer 구조를 대략적으로 볼 수 있는데, 크게 Multi-branch low rank down projection – GeLU – Multi-branch low rank up projection으로 구성되어 있습니다.
학습을 통하여 사전학습된 모델의 특징 공간을 새로운 task로 변환하는 이상적인 행렬 \hat{W} 를 근사화하는 것이 저자들의 목표라고 하며, 이러한 근사화된 행렬 \hat{W} 는 원래의 W와 동일한 크기이지만 더 적은 자유도를 가진다고 생각하시면 됩니다.
구체적으로 W에 대하여 3개의 low-rank 행렬들 P \in \mathcal{R}^{\beta \times m}, K \in \mathcal{R}^{\beta \times \beta}, Q \in \mathcal{R}^{\beta \times n} 를 분해를 할 수 있습니다.
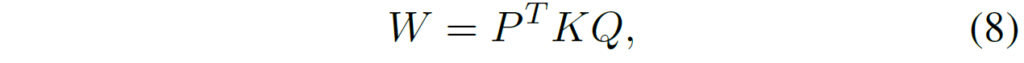
여기서 P와 Q는 \beta < min(m, n) 를 보장한다고 합니다. 그리고 K는 커널 행렬로 간주되어 LoRand의 파라미터 크기를 조절할 수 있는 역할입니다. 즉 커널 행렬 K의 크기인 베타값들이 몇인지에 따라서 LoRand를 구성하는 학습 가능한 파라미터의 크기가 결정된다는 것이죠.
아무튼 이러한 수식8의 연산은 multi-branch 구조로 구성되어 있는데, 이는 adaboost가 그랬던것처럼 low-rank 행렬들의 안정성과 강인성을 키우기 위함이라고 합니다.
즉 모든 W들은 \alpha 개의 브랜치들로 구성이 되어서 수식 8을 다음과 같이 재작성할 수 있습니다.
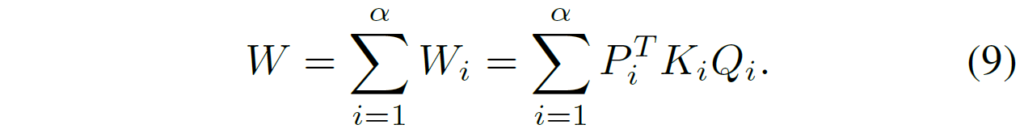
또한 kernel 행렬 K의 경우 각 브랜치 내부에 up/down 2개의 projection layer에 대하여 모두 활용이 되는 (즉 공유되는) 행렬이기에 더 파라미터 효율적이라고 저자는 주장하며 또한 두 투영 레이어 사이에 통일성을 촉진한다고 주장합니다.
아무튼 이러한 Up projection과 Down projection 레이어 대한 가중치들은 아래 수식으로 표현할 수 있습니다.
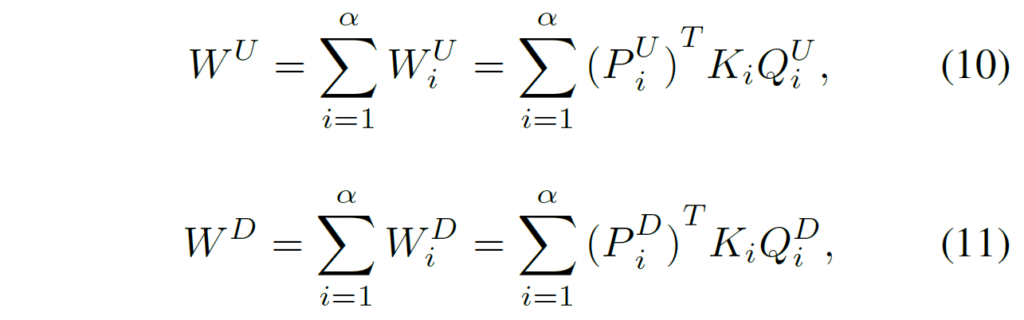
수식10,11에 대한 과정을 아래 그림으로도 확인하실 수 있습니다.
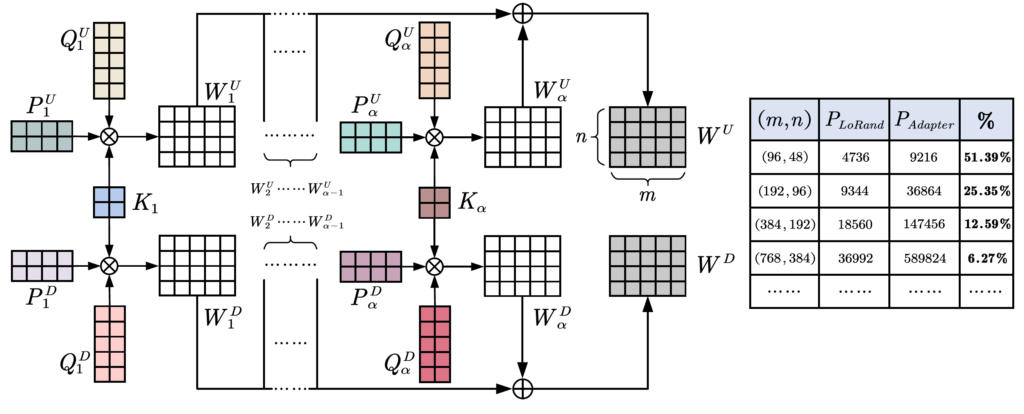
동일한 크기의 projection 행렬을 가질 시 파라미터의 효율성을 나타낸 것.
Parameter Analysis
그래서 이러한 low-rank approximation 과정을 수행하면 얼마나 파라미터 효율적인 것이냐는 물음에 저자들은 기존의 adapter 구조와 approximation 기반 구조에 대한 파라미터 수를 비교하였습니다.
adapter에 대하여 m 길이의 차원을 가진 입력이 들어왔을 때, down projection 이후의 middle layer의 차원을 n이라고 합시다. 그러면 각 adapter에 대하여 파라미터의 개수는 bias를 제외하였을 때 2mn 꼴로 나타날 수 있습니다.
일반적으로 adapter는 각 backbone의 블록마다 2개씩 존재하기 때문에 backbone의 블록이 \gamma 개 있따고 하면 아래와 같은 공간 복잡도를 가지게 됩니다.
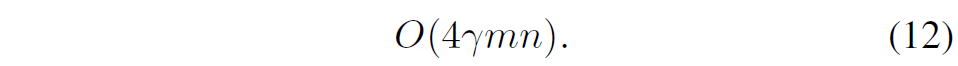
반면에 LoRand의 경우에는 위에서도 다뤘듯이 P, Q, K 행렬이 \alpha 개의 집합으로 구성이 되어 있습니다. 즉 \alpha (m\beta + \beta^{2} + n\beta) 만큼 존재하는 것이죠.
여기서 Up/down projection weight가 2개이면서 동시에 K의 경우 2개의 weight에 대해 공유를 하기 떄문에 다음과 같이 파라미터의 양을 표현할 수 있습니다.
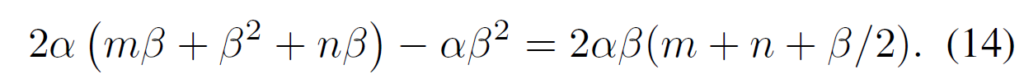
그리고 LoRand 역시 각 블록마다 2개씩 존재하기 때문에 수식 (14)에 대하여 블록의 개수 * 2배씩 더 곱해주어야 합니다.
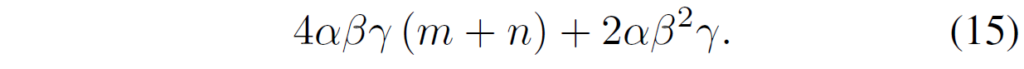
여기서 알파 베타 감마는 m과 n 사이에 최소값보다 더 작아야하기 때문에 다음과 같이 표현할 수 있다고 합니다.
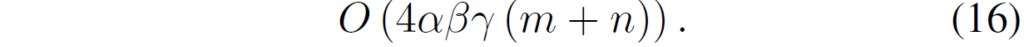
Adapter에 대한 공간 복잡도 수식 12와 LoRand의 공간 복잡도 수식 16 사이에 크기 비교를 단순히 하기 위해서, 식들을 간략화 해보면 다음과 같습니다.
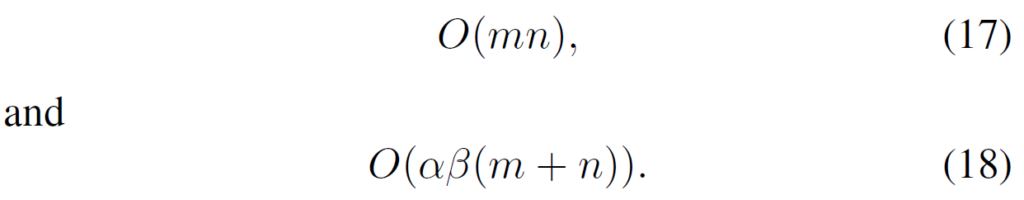
즉 Adapter의 경우 m과 n의 곱으로 표현이 되지만, LoRand의 경우 m과 n의 합으로 구성이 되기 때문에 더 효율적이다~라고 저자들은 주장합니다. 알파 값과 베타 값이 m과 n 의 최소값 보다 훨씬 작게 설정한다는 가정아래에서는 LoRand가 효율적으로 보이긴 합니다만 만약 스케일을 비슷하게 가져가게 될 경우에는 오히려 LoRand가 연산 복잡성이 더 클거 같긴 해서 알파 베타 값 설정을 잘 해야할 것으로 판단되네요. 참고로 저자들은 구현 당시에 알파를 2, 베타를 8의 값으로 사용했기 때문에 m과 n가 모델 복잡도에 더 지배적이라고 판단한 것 같습니다.
Experiments
그럼 이제 실험 섹션에 대해서 다뤄보겠습니다. 실험의 기본적인 세팅에 대해서 먼저 설명드리면, 앞서 소개드렸다시피 ImageNet-22K로 사전학습한 Swin Transformer를 본 논문에서는 기본 모델 세팅으로 가져가며, 여기서 3가지의 학습 세팅을 구분 짓는다고 합니다.
- FULL : 모델의 모든 파라미터를 학습하는 방식
- Fixed: Swin backbone의 사전 학습된 파라미터를 고정시키고, neck, head와 같은 downstream task를 위한 모델의 다른 구조들은 학습하는 방식?
- Adapter: 2개의 학습 가능한 adapter 구조를 각 Swin block마다 추가하고, 이때 backbone과 관련된 모든 파라미터들은 freeze 시키는 adapter tuning 실험 세팅. 여기서 Aadapter-B와 Adapter-T로 나뉘는데 B와 T의 차이는 adapter 내부의 middle layer의 차원(D_{ML} )를 입력 차원의 절반만 사용할지, 1/4를 사용할지 라고 함.
그리고 LoRand 내부의 구성 세팅은 다음과 같습니다.

평가에 사용하는 task는 크게 Object Detection과 Semantic Segmentation으로 설정되어 있습니다.
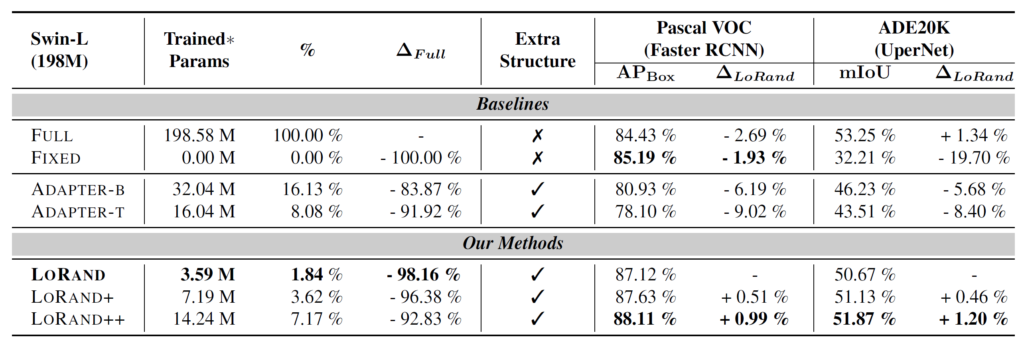
먼저 첫번째 표를 살펴보시면, 검출 성능의 경우 매우 이상적이게도 모델을 전체 fine-tuning한 FULL과 학습을 전혀 하지 않은 Fixed와 비교하였을 때 논문에서 제안하는 LoRand adapter를 사용할 경우 성능이 더 향상되는 것을 볼 수 있습니다.(84.43/85.19 vs 88.11%)
이게 Adapter를 추가해서 모델의 크기가 더 커졌기 때문에 성능이 오르는 것이 당연한 것아니냐? 라고 생각하실 수도 있는데, 일반적인 Adapter를 추가하게 될 경우에는 오히려 성능이 5~7% 가량 더 하락하는 것을 보실 수 있습니다. 이를 통해서 단순히 adapter만을 추가한다고 해서 좋은 결과를 얻는 것은 또 아니라는 것을 확인할 수 있습니다.
물론 Semantic Segmentation의 경우에는 전체 모델을 fine-tuning하는 것이 가장 좋은 성능을 보여주긴 했습니다만, 모델 학습에 사용된 파라미터의 수가 92% 가량 차이가 난다는 점에서 놓고 봤을 때, 학습에 사용되는 리소스는 최소화하면서 모델의 성능 차이 폭은 1.5% 수준 이내로 나타낸 것입니다.
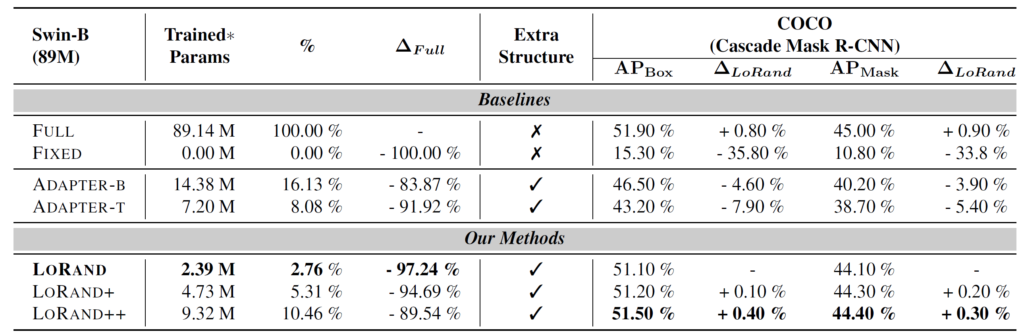
COCO 데이터 셋에 대한 검출 & instance segmentation 성능 역시도 아래 표에서 확인 가능하듯이 유사한 결과값을 보여주고 있습니다.
다음은 ablation study 관련입니다.
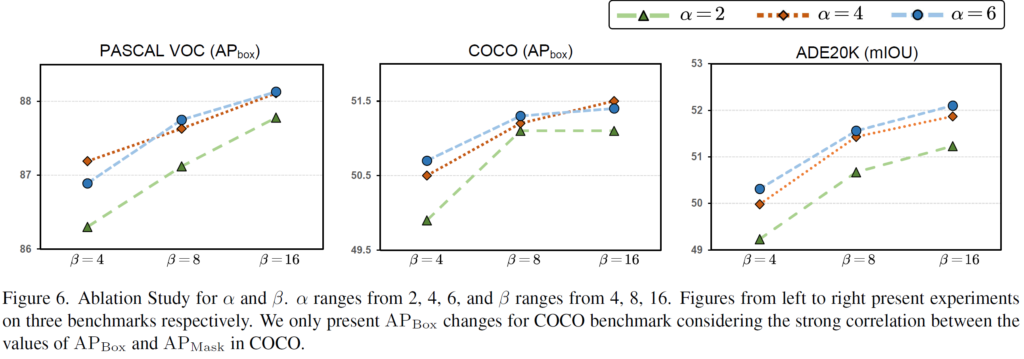
사실 논문에서 제안한 LoRand block에서 ablation study를 할만한 것이 딱히 없는데, 대략 알파값과 베타 값을 어떻게 설정하는 것이 모델 성능에 유의미한가에 대한 실험입니다.
당연한 말이겠지만.. 대략적인 경향은 알파와 베타 값이 크면 클수록 좋긴 합니다. 물론 COCO 데이터 셋의 경우에는 베타 값이 무작정 크타고 해서 성능의 향상을 반드시 보장하는 것은 아니지만 대부분은 그러합니다. 근데 저자들이 알파랑 베타 값을 키울수록 모델의 파라미터가 대략 얼만큼 증가하는지 FLOPs나 파라미터 수를 좀 함께 보여줬으면 좋았을텐데 그런 부분은 쏙 뺏네요.
결론
low-rank approximation라는 개념에 대해서 익숙치 않으셨던 분에게는 어찌보면 참신하게 와닿을지도 모르겠습니다. 하지만 논문이 아쉬운 점들이 많이 존재합니다. 먼저 왜 그냥 adapter를 사용하면 모델의 성능이 떨어지지만, low-rank approximation을 활용하여 파라미터 수를 효율적으로 줄인 adapter를 사용한 경우에는 성능이 개선되는가에 대한 질문에 저자들이 그럴듯한 설명을 하지 못하고 있습니다.
아마도 실험적으로 해보니깐 이게 되네? 싶어서 논문을 쓴 것 같긴한데.. 왜 low-rank approximation을 통한 파라미터 수 감소를 시켜야만 tuning 성능이 좋아지는지를 설명했으면 좋았겠네요.
사실 그냥 adapter의 경우에도 tuning 관점에서 학습해야할 파라미터의 수가 7M정도 수준이라서 그렇게 많다고 비춰지지는 않는데.. LoRAND++의 경우 9.32M로 학습해야하는 파라미터 수가 더 많긴 하거든요. 그럼에도 tuning 시 성능 하락이 없고 오히려 잘 나온다는 것은 low-rank approximation이 단순히 메모리 효율적이다라는 측면 뿐만 아니라 어떠한 다른 기전이 또 작용한게 아닐까 싶습니다.
게다가 추론 속도도 따로 언급하는 게 없어서 그 부분도 좀 아쉽긴 하네요. 사실 파라미터 수도 중요하지만 추론 속도도 중요하다고 생각이 들어서, 그런 부분을 함께 넣지 않은 것이 아쉽고 또 코드도 공개 안되어있다보니 아쉬운 점이 여럿 존재하는 논문입니다.
안녕하세요 정민님, 좋은 리뷰 감사합니다.
제가 아직 많은 논문들을 읽어보고 follow up 한 단계가 아니라서, 처음 보는 표현들과 아직 이해가 덜 된 모델들이 있어 구글링을 통해 간단하게나마 개념을 훑어보며 리뷰를 읽어보았습니다.
그럼에도 불구하고 Intro 부터 결론까지 천천히 읽어보면 흥미로운 내용 투성이었는데요.
초거대모델인 foundation model은 학부관점에서 배웠던 fine-tuning 패러다임이 통하지 않는다는 것과, 이를 해결하기 위해 Adapter를 도입하여 pretrained모델을 구성하는 각 블록 사이 사이에 학습 가능한 bottle-neck 구조를 추가하고, 기존 사전학습 파라미터들은 freeze하고 Adapter만을 파라미터 튜닝하는 구성이 정말 신기했습니다.
여기에 더해 기존의 adapter를 LoRand 형식의 layer로 바꾸면서 파라미터수를 감소시키는 효과를 가져간 것 또한 신기했습니다.
질문이 하나 있습니다.
수식 7 에서, low-rank approximation에서는 bias보다 weight이 더 중요한 파라미터라는 것을 염두해두라고 하셨는데, 그 이유가 무엇인가요?
이후에 Parameter Analysis에서도 각 adapter에 대해 파라미터 개수를 bias를 제외하였을 때로 표현했는데, bias가 그다지 큰 영향을 미치지 않기 때문에 단순히 제외시키는 것으로 이해하면 될까요?
추가로 정민님의 결론을 보며 논문을 읽을 때 비판적인 시각이 왜 필요한 것인지 다시 한번 느꼈습니다!
감사합니다.
안녕하세요.
수식7 관련해서 답변드리면, 인공지능에서 모델을 구성하는 레이어 하나하나 들은 대부분 y = Wx + b 꼴로 되어있음은 알고 계실겁니다. 여기서 입력 x의 shape이 데이터 개수 (N) x 데이터 차원 (D) 라고 했을 때 W의 shape은 D x 출력 차원 (C) 꼴로 표현됩니다. 만약 레이어 하나의 모델이고 output이 하나의 실수로 나타나는 회귀 문제 같은 경우에는 W가 D x 1이 되겠죠. 그리고 여기서 bias는 이 W의 출력 차원 크기에 맞춰서 C x 1꼴로 나타납니다.
즉 bias는 말 그대로 가중치 W를 통해 새로운 공간으로 데이터가 투영되었다면 투영된 결과값들이 여기서 얼만큼 더 이동해야하는가를 수행하는 단순한 덧셈 연산에 불가합니다. 즉 데이터를 새로운 latent space(대충 함수를 통해 새로운 의미를 가지는 차원?으로 이해하면 될 것 같네요)로 투영시키는 W 파라미터가 더 중요하지 bias는 사실 어떠한 대상을 추론하는데 있어 상대적으로 중요한 파라미터는 아니긴 합니다.
그래서 종종 y = Wx + b를 다 표현하지 않고 y = Wx 꼴로 많이들 생략해서 표현하기도 하고, 실제 구현 단계에서도 torch에서 bias 옵션을 false로 해두는 경우도 많이 있습니다. pytorch에서 FC layer나 Convolution을 처음 선언할 때 Weight를 선언해주기 위해서 Input dimension, Output dimension을 선언해주어야만 하지만 bias는 True False 옵션으로 설정할 수 있다는 것 자체에서 무엇이 더 비중있는 파라미터인지 알 수 있을 거라고 생각합니다.
결론은 bias라는 파라미터는 수 많은 레이어로 구성된 딥러닝 모델 관점에서 그렇게 중요한 파라미터가 아니라고 여겨지고, 이때문에 실제 사용 여부와 관계없이 연산량 계산 관점에서 생략을 많이들 한다고 이해하시면 좋겠습니다.
감사합니다.
리뷰 잘 읽었습니다.
전체 학습을 엄두내지 못할 정도로 큰 foundation 모델들이 붐을 불러일으키고 있는 이런 상황 속에서 이 adapter 라는 녀석을 잘 활용한다면 여러 vision task들에서 좋은 결과가 나올 거 같네요.
저번주에 리뷰해주신 [ICLR2023] paper와 본 paper에서 설계하는 pipeline의 구조를 보니 adapter의 삽입 위치? 가 다른 거 같더라구요.
통상적으로 adapter를 ViT 외부에 두는지, 아니면 본 논문처럼 transformer block 내에 구성하게 되는지 궁금합니다.
감사합니다.
안녕하세요.
저도 Adapter 논문을 이제 막 읽기 시작한거라 사실 정확하지는 않지만, 이 논문을 읽었다는 관점에서는 내부에다가 두는 것이 근본인 것 같습니다. NLP쪽 애들이 그렇게들 하나봐요. 근데 사실 ViT 외부에 두냐 내부에 두냐는 취향차이라고 여겨집니다. 애초에 지난번에 리뷰한 논문은 ViT 백본에다가 CNN의 특징을 추가해주고 싶은 것이 핵심이었기 때문에, 내부에서의 CNN 연산보다는 바깥으로 빼서 정보를 주입하는 injection 컨셉이 더 어울렸다고 보여지네요.
즉 자신이 어떠한 의도로 adatper를 쓰고 싶은지에 따라서 백본의 내부에 삽입할지 외부에 삽입할지를 결정하면 될 것 같습니다.
감사합니다.