Speech Recognition Domain 정리

안녕하세요. URP를 마치고 3주가 지나고 이렇게 첫 X-REVIEW를 작성하는 시기가 왔네요. 이번 X-REVIEW는 논문 리뷰가 아닌 음성 도메인과 관련하여 공부한 것을 정리한 글입니다.

간략하게 목차를 작성하였으니 참고해주시면 좋을 것 같습니다.

<목차>
1. 소리(Sound)
1.1 물리 음향
1.2 심리 음향 (Psychoacoustic)
2. 디지털 신호 처리
2.1 Sampling (표본화)
2.2 Quantization (양자화)
3. Fourier Transforms (푸리에 변환)
3.1 푸리에 변환 접근
3.2 푸리에 변환식 유도 과정
3.3 Discrete Fourier Transform (DFT)
3.4 Fast Fourier Transform(FFT)
3.5 Short Time Fourier Transform (STFT)
4. Feature Extraction
4.1 Pre-emphasis
4.2 Framing
4.3 Windowing
4.4 Fourier Transforms
4.5 Spectrum & Power Spectrum
4.6 Mel Filter Bank
4.7 Log Mel Spectrogram
4.8 IDFT (or DCT)
4.9 MFCC

1. 소리 (Sound)

소리는 어떻게 발생하는 걸까요? 소리는 진동으로 인한 공기의 압축으로 생성됩니다. 여기서 압축이 얼마나 되느냐를 wave(파동)으로 표현할 수 있습니다. 파동은 진동하며 공간/매질을 전파해 나가는 현상인데, 질량의 이동은 없지만 에너지/운동량의 운반은 존재합니다.

1.1 물리 음향

그렇다면 여기서 말하는 에너지/운동량이 뭘까요? 소리에서 얻을 수 있는 물리량(운동량)은 크게 3가지가 있습니다.

• Amplitude(Intensity) : 진폭
• Frequency : 주파수
• Phase (Degress of displacement) : 위상

https://velog.io/@p2yeong/오디오-처리Audio-Processing (이미지 참고)

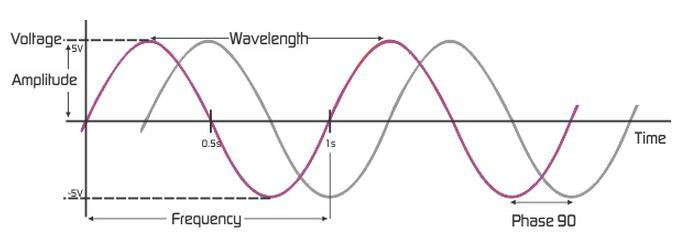
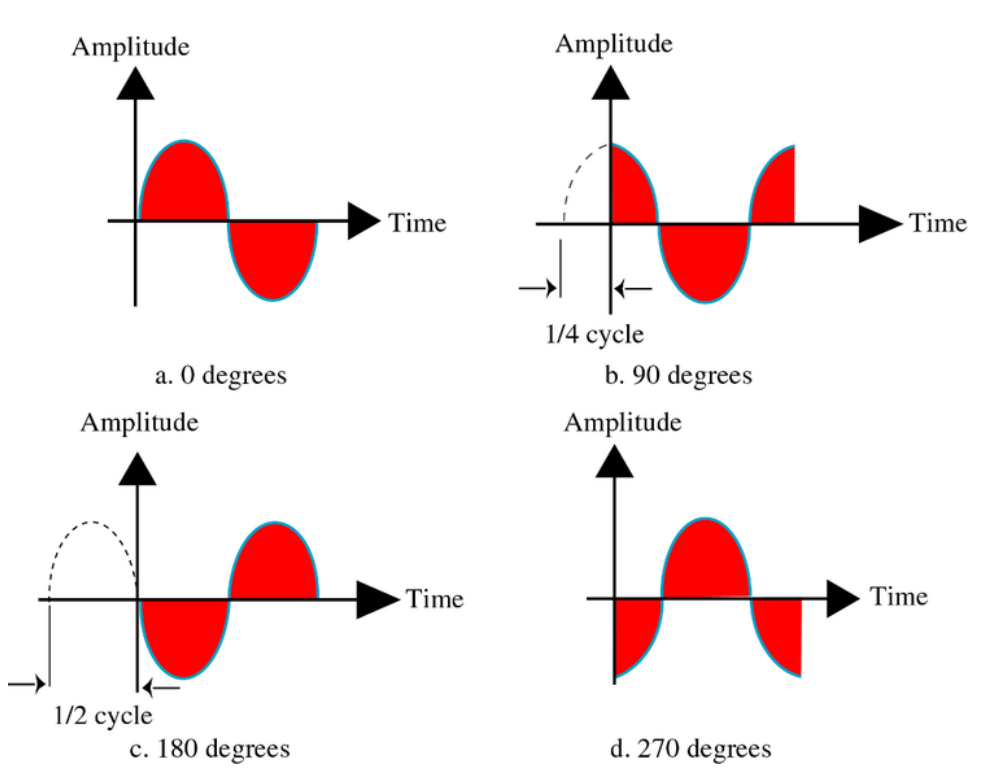
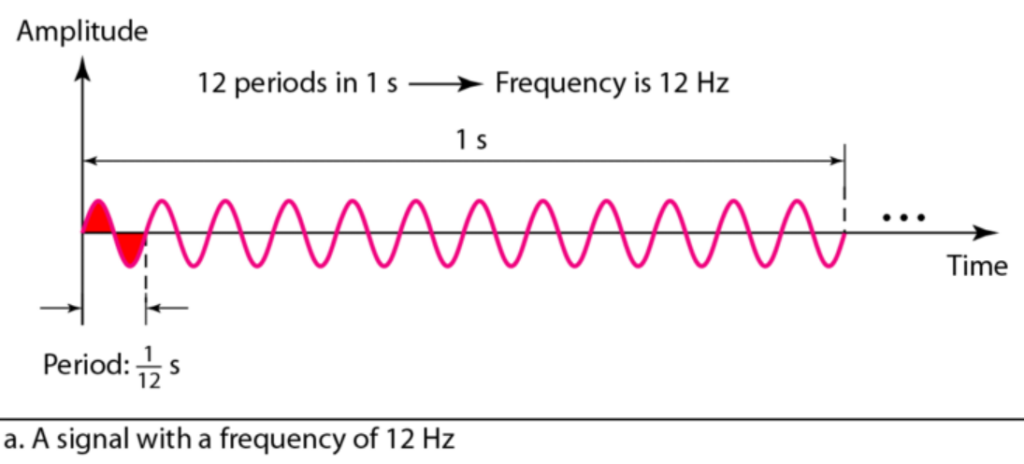
위의 그래프는 위상의 차이를 쉽게 파악할 수 있도록 그려진 그래프인데, 위상(Phase)은 동일 주파수에서 시간차/어긋남 등을 표현하는 양입니다. 시간 0시에 대한 파형의 상대적인 위치를 말합니다. 진폭(Amplitude;Intensity)은 신호의 세기(음성의 크기) 혹은 신호의 높이를 말합니다. 주파수(Frequency)는 1초에 완성되는 주기의 횟수, 1초 동안 생성되는 신호 주기의 수를 말합니다. 단위는 Hz입니다. 주기(Period; Wave length)는 한 사이클을 도는 데 걸리는 시간으로 몇 초에 한번 반복이 되는지 파악할 수 있습니다. 단위는 s 입니다. 아래 그림을 통해 T = 1/f를 확인할 수 있습니다.

1.2 심리 음향 (Psychoacoustic)

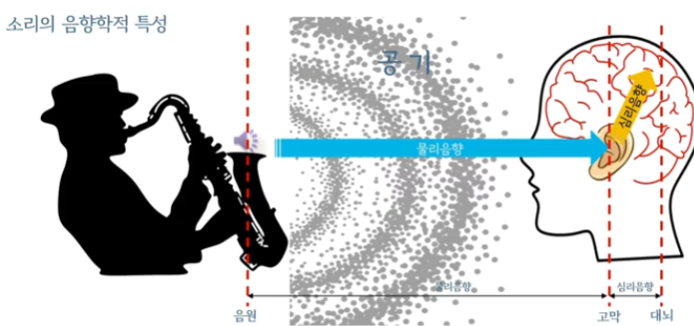
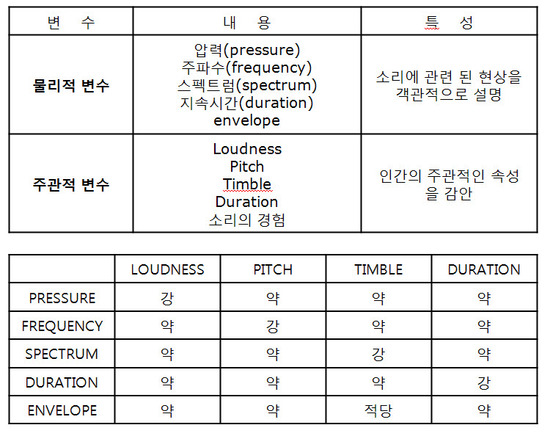
위에서 언급한 주파수, 위상 등은 소리가 갖는 자연적인 고유의 음향학적 특성으로 물리 음향이라 불립니다. 물리 음향과 같이 업급되는 것으로는 심리 음향이 있습니다. 소리가 청각을 통해 청각신호로 변환된 이후에 대뇌에서 일어나는 음향학적 특성을 심리 음향이라고 합니다. 심리 음향과 관련된 용어로는 Loundness(소리 크기), pitch(음정, 소리의 높낮이/진동수), Timble (음색, 소리 감각) 등이 있습니다.
(더 자세하게 알고 싶다면 여기 참고 https://www.youtube.com/watch?v=fIbgW-gGwBQ&list=PLcOmWKTcXBwjJdpFgNnvchz81nxMCs7rl&index=18)

2. 디지털 신호 처리

우리가 듣는 음성은 analog 신호입니다. 여기서 말하는 analog 신호는 시간을 축으로 가지는 연속적인 신호를 말합니다. 이러한 아날로그 신호는 컴퓨터와 같은 전자기기에서는 다룰 수 없기 때문에 아날로그 신호를 기계가 다룰 수 있는 디지털 신호로 바꿔주는 과정이 필요합니다. 먼저, 시간축을 따라 sampling(표본화)을 진행합니다.

2.1 Sampling (표본화)

sampling은 일정한 시간 간격 마다 음성 신호를 샘플해서 continuous singal을 discrete singal로 변환시킵니다. 샘플링 간격에 따라 amplitude를 측정하는데, 1초의 연속적인 신호를 몇개의 숫자들의 sequence로 표현할 것인가를 sampling rate f_s 라고 합니다. sampling rate는 Hz단위를 사용합니다. sampling rate가 클 수록, 원본 데이터와 비슷해지지만 그만큼 저장해야 하는 데이터의 양이 늘어나게 됩니다. sampling rate가 작게 되면 aliasing이 일어나게 되는데 이런 경우 원본 데이터로 복원하는데 어려움을 겪을 수 있습니다. sampling rate가 낮은 경우 원래 신호보다 주파수가 낮은 검은색 점선 형태로 복원될 수 있습니다.

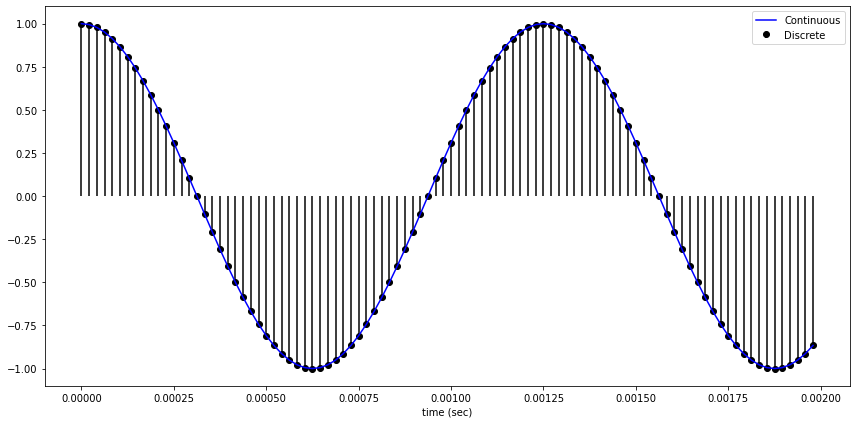
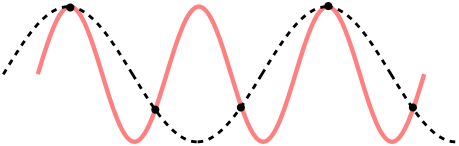
sampling을 어느정도로 해야 원래 신호로 복원할 수 있는지에 대한 고민은 Nyquist Theorem이 해결해줄 수 있습니다. 나이쿼스트 정리는 원래 신호가 가진 최대 주파수의 2배 이상으로 샘플링하면 원래 신호를 충분히 재생할 수 있다는 정리 입니다. (f_s는 sampling rate/sampling frequency, f_m는 신호의 최대 주파수)

f_s = 2f_m

사람의 가청 주파수는 20~20kHz이기 때문에 대부분은 나이쿼스트 정리를 이용하여 sampling rate를 오차를 고려해 44100Hz로 sampling 합니다.

2.2 Quantization (양자화)

양자화란 실수 범위의 이산 신호를 정수(integer) 이산 신호로 바꾸는 것을 의미합니다. sampling은 time인 x축을 기준으로 이산화 했다면, 양자화는 amplitude인 y축을 기준으로 이산화 진행했다고 생각하면 편합니다. Bit depth라는 변수를 통해 몇 비트로 양자화를 할 것인지 결정할 수 있습니다. B bit의 Quantization의 경우 -2^{B-1} ~ 2^{B-1} -1 구간으로 이산화 됩니다. 양자화도 마찬가지로 bit를 많이 줄수록 원래 음성 신호의 정보 손실을 줄일 수 있지만 그만큼 저장 공간이 늘어나는 단점이 있습니다.

아래 그림을 통해 표본화, 양자화를 확인할 수 있습니다.

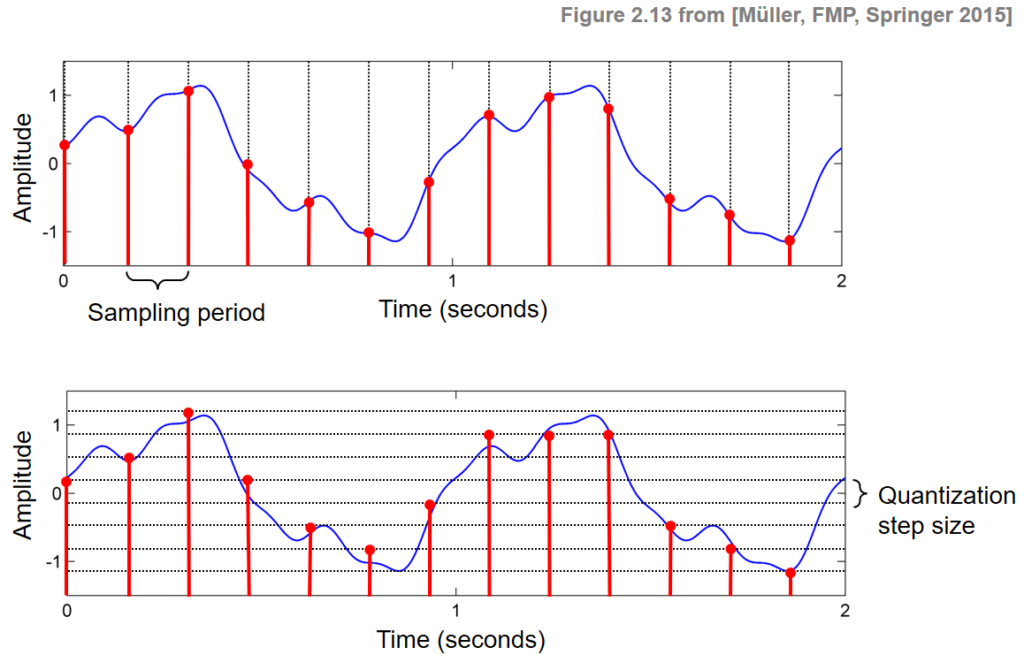
이렇게 샘플링과 양자화를 통해 음성 데이터를 디지털화 시켰습니다. 이 이후는 이렇게 변환한 데이터를 어떻게 가공해야 하는지 작성해보겠습니다.

3. Fourier Transforms (푸리에 변환)

앞에서 그림으로 나온 신호들은 거의 대부분 단순한 사인파 형태로 신호가 그려져 있었습니다. 하지만 현실에서는 이렇게 하나의 웨이브인 단순파(simple wave)로 그려지는 경우가 없습니다. 대부분 여러 웨이브로 구성된 복합파(complex wave)로 구성된 경우가 많기 때문에 분석이 어렵습니다. 푸리에 변환은 복합파를 여러개의 단순파의 합으로 나타낼 수 있도록 합니다. 아래는 푸리에 변환 전급 방식과 변환식 유도 과정을 작성하였습니다.

3.1 푸리에 변환 접근

복잡한 파형의 그래프를 보고 어떻게 해야 순수한 진동수로 다시 분해할 수 있을까요? 첫 번째, 소리의 진동수를 주기 함수로 나타냅니다. 두 번째, 주기 함수를 임의의 간격으로 감아 새로운 함수를 그립니다.

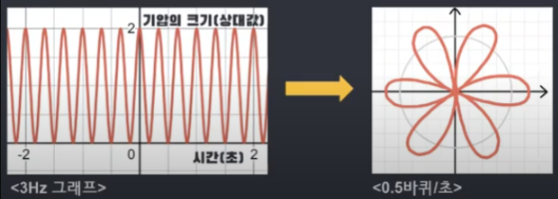
위의 그림을 예시로 설명하자면, 1초에 3번 진동하는 신호 자체의 진동수가 있고 1초에 원을 반바퀴 도는 감긴 그래프의 진동수가 있습니다. 여기서 중요한 점 두가지가 있는데, 첫 번째는 감긴 그래프의 진동수는 우리가 임의로 설정하는 것이 가능하다는 것입니다. 두 번째는, 원함수 3Hz 그래프를 복소평면 단위원에 따라 감고 있다는 것입니다.

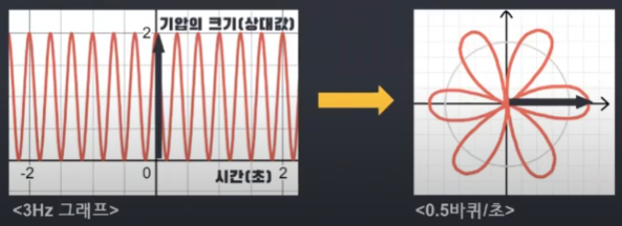
매 시점에서 오른쪽 그래프의 벡터 크기는 그 시점에서 원래 그래프의 높이와 같습니다. 그래프의 높은 점을 원점에서 먼 거리에 대응하고, 낮은 점은 원점에서 가까운 거리에 대응합니다.

감긴 그래프의 진동수를 임의로 설정할 수 있다고 하였는데, 만약 감긴 그래프의 초당 도는 바퀴수를 다르게 설정하면 어떻게 될까요? 이럴 경우 감긴 그래프가 다른 형태로 그려지게 됩니다. 아래의 그림으로 확인할 수 있습니다. (0.5Hz → 1.5Hz)

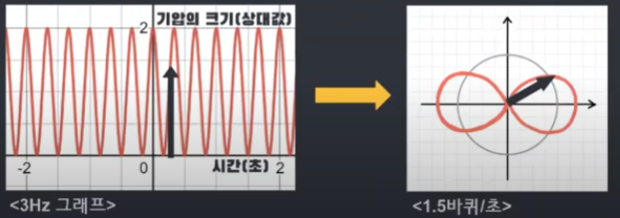
그렇다면 초당 도는 바퀴수를 원래 진동수와 동일한 3으로 설정하면 어떻게 될까요? 신호 자체의 진동수와 감긴 그래프의 진동수를 동일하게 설정한다면, 신호 그래프의 높은 점은 모두 오른쪽에 몰리고 남은 점은 왼쪽에 몰리는 것을 확인할 수 있습니다. (아래 그림을 통해서 확인 가능)

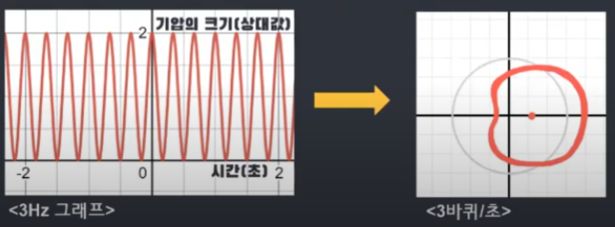
위의 내용을 인지한 상태에서 그래프를 질량이 있는 철사라고 생각해봅시다. 그래프를 질량이 있는 철사라고 생각하고 무게 중심에 대해 생각해 볼때, 무게중심은 대부분 원점 부근에 존재하지만 아래 그림에서 초당 도는 바퀴수가 진동수와 같을 때인 3번째 그래프를 보면 무게중심이 예외적으로 오른쪽에 치우치게 되면서 특이한 무게중심의 위치를 가지게 되는 것을 확인할 수 있습니다. (아래 그림의 하트 모양이 무게 중심을 의미함)

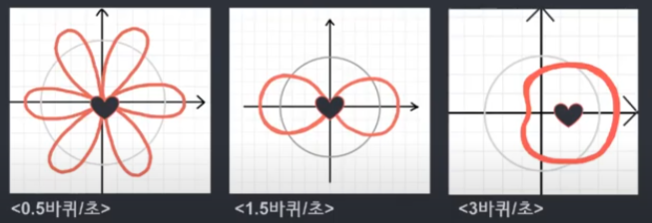
원래 그래프의 진동수와 초당 도는 바퀴수가 같은 경우에 무게중심이 특이한 위치에 생긴다는 것을 이용하여 여러 코사인파가 합쳐져 있을 때 합쳐지기 전 순수한 코사인파의 진동수를 추론할 수 있습니다.

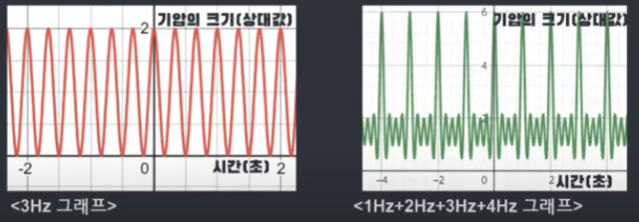
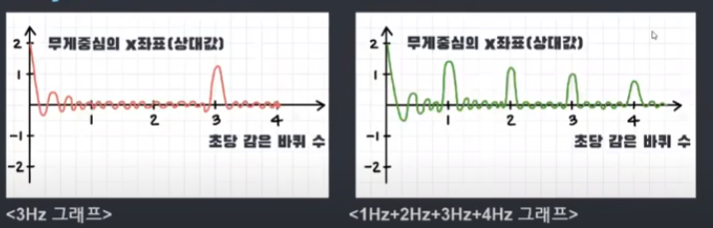
무게 중심은 대부분 원점 부근에 위치하다가 초당 감은 바퀴수가 원래 그래프의 진동수와 일치하는 경우에만 오른쪽 으로 치우쳐서 위치하게 되므로 무게중심을 좌표평면 위에있는 점이라고 생각하고 초당 감은 바퀴수에 따른 무게중심의 x좌표를 그래프로 나타내면 그래프가 뛰는 지점이 발생합니다. 이때, 그래프의 뛰는 지점이 원래 그래프의 진동수인 것을 확인할 수 있습니다. 아래 그림을 보시면 3Hz 그래프와 1부터 4Hz까지 합쳐진 그래프가 있습니다. 이것을 위에 설명한 것처럼 무게중심의 x좌표 그래프를 그리게 되면 아래처럼 뛰는 지점을 확인할 수 있는데 뛰는 지점이 원래 그래프의 진동수인 것을 확인할 수 있습니다.

3.2 푸리에 변환식 유도 과정

위에서 푸리에 접근에 대해서 설명드릴 때는 무게중심의 x좌표에 대해서만 고려하였는데, 2차원 공간에 있기 때문에 y좌표도 고려해야 합니다. 이때 무게 중심을 복소평면에서 다루는데, 복소수는 회전과 감기를 잘 설명할 수 있기 때문입니다.

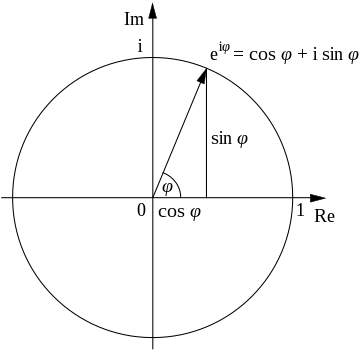
오일러 공식이 이를 잘 설명할 수 있는데, e에 ix 제곱을 취했을 때, 그 점은 복소 평면에서 단위원을 따라 딱 x rad을 회전한 점과 같습니다. 아래 그림에서 e에 2i제곱한 점을 확인할 수 있는데 이는 2만큼 이동했다는 것을 알 수 있습니다.

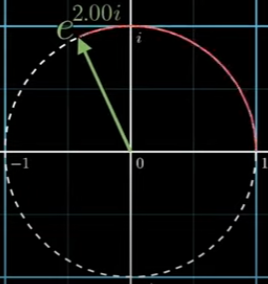
이것을 이용해서 1초에 단위원을 한 바퀴 도는 것을 표현할 수 있는데, e^{2πit}로 표현할 수 있습니다. 여기서 t는 흐른 시간, 2π는 2π rad, 즉 단위원의 둘레의 길이를 의미합니다. 지수에 진동수 f를 곱해 단위원이 도는 속도를 조절할 수 있습니다. 푸리에 변환에서는 관습적으로 시계방향의 화전을 다루기 때문에 지수에 마이너스를 곱해 줍니다. (직교 좌표계에서는 x축에 대한 각을 측정할 때 시계 방향 각에 (-)를 매기기 때문입니다) 설명한 것을 정리하여 최종적으로 e^{-2πift}로 표현할 수 있습니다.

어떤 신호를 g(t)라고 표현해보겠습니다. g(t)를 e^{-2πift}에 곱하면 회전하는 복소수는 g(t)의 값에 영향을 받아서 커졌다 작아졌다를 반복할 것입니다. 이를 반복하면 원래 그래프의 감긴 그래프를 그리게 됩니다. ⇒ g(t)e^{-2πift} (진동수 f를 변수로 그래프를 원에 감는 행위를 수식으로 표현)

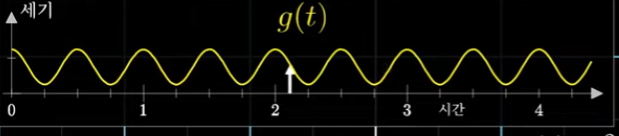
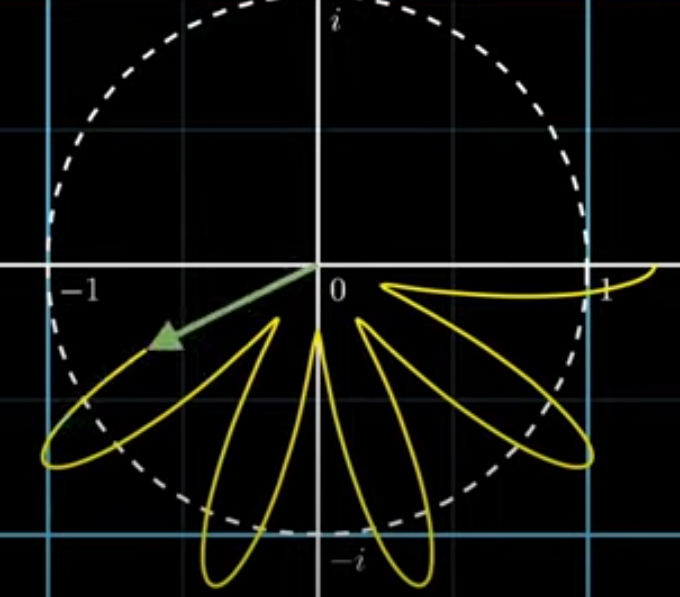
그렇다면 원래 이 감긴 그래프의 무게중심의 위치를 추적하는 것은 어떻게 할까요? 원래 시간에서 수많은 시점을 고른 다음에 각각의 점이 원래 그래프에 어느점에 대응하는지를 확인한 다음 평균을 취합니다. 이 근사는 점의 개수가 늘어날수록 정확해지기 때문에 극한을 취하면 이 행위는 함수의 적분을 취한뒤 구간의 길이를 나누는 것이 됩니다.

{1\over{t_2-t_1}}\int_{t_1}^{t_2}-g(t)e^{-2πift}dt (⇒ 감긴 그래프의 무게중심을 가리킨다)

이 식에서 실제 푸리에 변환 식과 차이가 있는 부분이 있는데, 실제 푸리에 변환 식은 시간 구간으로 나누지 않습니다. 푸리에 변환은 이 식의 적분 부분만 가리키는데, 무게 중심 자체를 보는 것이 아니라 벡터에 일정량이 곱해진 값을 보기 때문입니다.

원래 그래프에서 3초간을 관찰 구간으로 설정했다면, 무게중심의 백터에 3이 곱해지게 되게 됩니다. 구간의 길이가 6초였다면, 무게중심에 6이 곱해지게 됩니다. 물리적으로 어떤 진동수가 오랜 시간 지속될수록 그 진동수에서의 푸리에 변환 값이 커지게 되는 효과가 있습니다.

예를 들어서 진동수가 1초에 2번인 순수한 코사인파 신호가 있고, 감는 진동수를 똑같이 1초에 2바퀴로 하면 무게 중심은 변하지 않을 것입니다. 구간이 바뀌어도 모양은 바뀌지 않기 때문입니다. 하지만 신호가 오래 지속될수록 그 진동수에서의 푸리에 변환 값은 커질 것입니다. 하지만 두 진동수(원래 신호의 진동수와 감는 그래프의 진동수)끼리 아주 조금만 달라지더라도, 그래프가 고르게 분포하는 효과가 생기기 때문에 시간이 지나도 그 크기는 상쇄될 것입니다.

아래 그림들을 통해 상쇄되는 것을 확인할 수 있습니다.

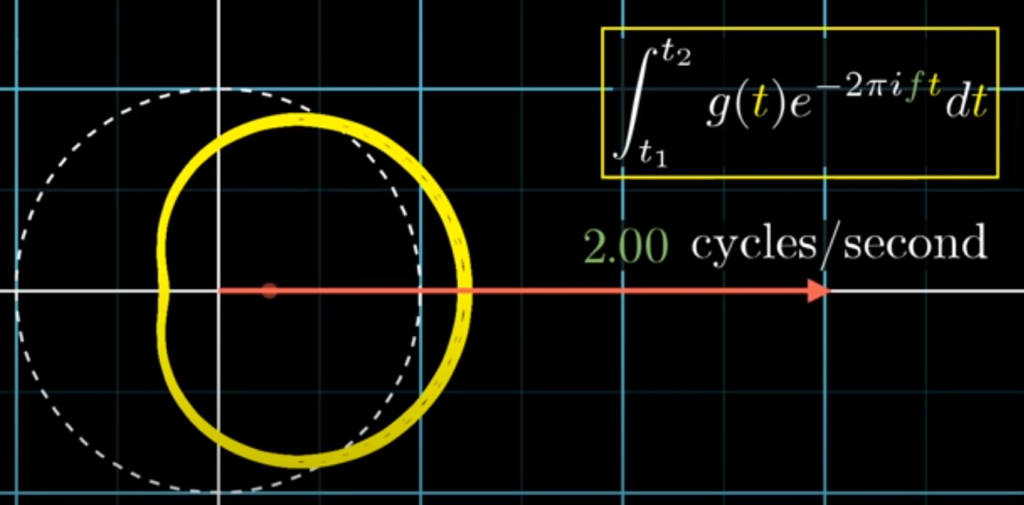
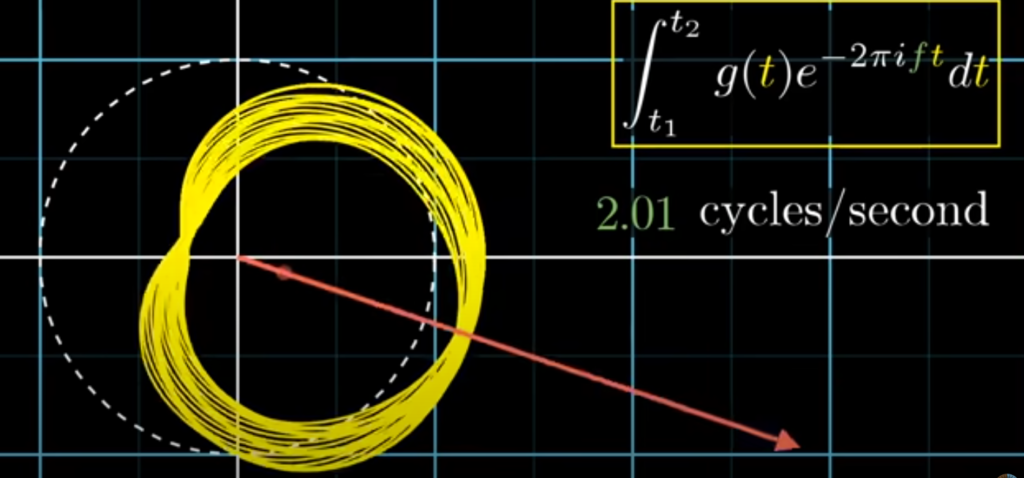
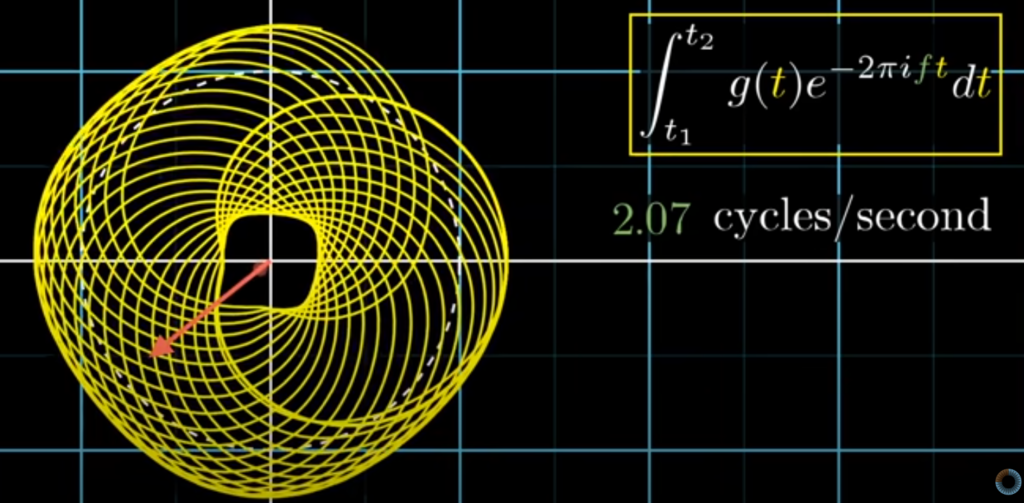
위의 설명한 것을 바탕으로 최종적으로 푸리에 변환 식은 아래와 같습니다.

X(f) = \int_{-\text{∞}}^{\text{∞}}x(t)e^{-2πift}dt 혹은

X(jw) = \int_{-\text{∞}}^{\text{∞}}x(t)e^{-jwt}dt ( 여기서 ω(각주파수/angular frequency)는 2πf를 의미합니다 )

푸리에 변환을 통해 time domain에서 연속적이고 무한한 길이의 신호를 frequency domain에서 연속적이고 무한한 주파수로 나타낼 수 있습니다.

3.3 Discrete Fourier Transform (DFT)

하지만 우리는 아날로그 신호를 discrete하게 바꾸주었기 때문에 위의 푸리에 변환 식을 discrete한 영역으로 바꿔주어야 합니다.

아래의 식은 Discrete Time Fourier Transform 입니다. 이 식으로부터 DFT를 구할 것입니다.

X(f) = \sum_{n=0}^{N-1}x[n]e^{-j2\pi\\fn}

DTFT의 수식을 살펴보면 x[n]과 X(f) 모두 연속 주파수 f를 가지고 있다는 것을 알 수 있습니다. 연속 주파수 f는 lim_{N->\infin}\frac{k}{N}에서 출발했기 때문에 아래처럼 DFT를 정의할 수 있습니다.

X[k] = \sum_{n=0}^{N-1}x[n]e^{-jk\frac{2\pi\\}{N}n}

우리가 가진 신호 x[n]에서, 이산 시게열 데이터가 주기 N으로 반복한다고 할때, DFT는 주파수와 진폭이 서로 다른 N개의 사인 함수의 합으로 표현이 가능합니다.

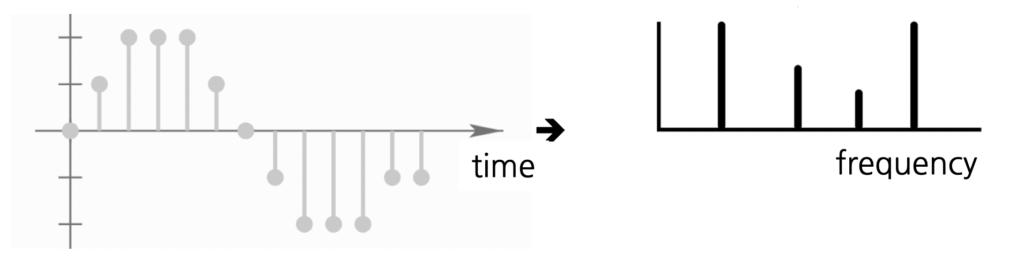
(위의 내용과 관련하여 더 자세하게 알고 싶다면 참고 (추천) https://angeloyeo.github.io/2019/07/14/Freq_Sampling.html)

3.4 Fast Fourier Transform (FFT)

FFT는 DFT의 방대한 계산량을 줄이고자 나온 알고리즘 입니다. 대부분의 신호처리 응용에서는 계산량을 줄이기 위해서 FFT 알고리즘을 사용합니다. X[k] 하나의 계산은 N개 항의 곱셈 및 (N-1)개의 덧셈이 필요합니다. 즉, N점 DFT(N-point DFT) 계산은 N^2번의 복소수 곱셈 등 방대한 계산이 필요합니다. 이를 알고리즘 효율성의 척도로써 볼 때, O(N^2) 만큼 걸립니다.

FFT는 DFT의 상수 및 종작의 대칭성을 이용하여 계산량을 줄였습니다. DFT를 길이가 짧은 여러 DFT로 계속 분할시켜 곱셈 량을 N에 비례하도록 하였습니다. 이 덕분에 O(Nlog_2N)만큼이 걸리게 됩니다.

(더 자세히 보고 싶다면 여기 참고 http://www.ktword.co.kr/test/view/view.php?m_temp1=2596)

3.5 Short Time Fourier Transform (STFT)

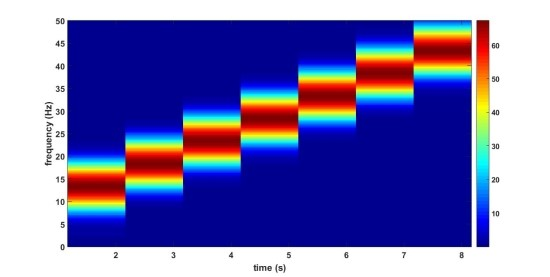
만약 아래의 그림처럼 시간에 따라 주파수가 변하는 신호가 있다고 가정해보겠습니다. 10Hz, 20Hz, 30Hz를 가집니다. 아래 두번째 그림을 보면 신호를 FFT 변환한 것을 확인할 수 있습니다. 각각의 주파수 영역대에 맞추어서 봉우리가 있는 모습을 확인할 수 있습니다.

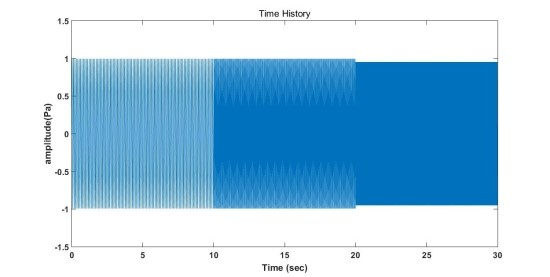
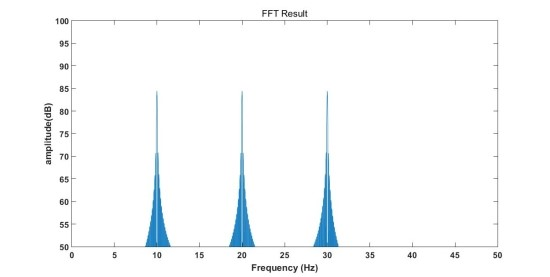
위의 FFT를 통해 우리가 알 수 있는 정보는 신호의 주파수 성분이 10Hz, 20Hz, 30Hz로 이뤄졌다는 것 뿐이고, 3가지 주파수 성분이 어느 시점에 존재하는지 여부는 알 수 없습니다. 이런 경우, 복잡한 신호일수록 알기 어려워지며 이에 따라 Time-Frequency 분석 기법인 STFT가 생기게 되었습니다. 위의 신호를 STFT 변환하면 아래 그림과 같은 결과를 얻을 수 있습니다. 그래프를 자세히 보면 시간과 주파수 2개의 축으로 이뤄져 있는 것을 확인할 수 있습니다. 이렇게 spectrum을 시간 순서대로 이어 붙여 time domain으로 나타낸 것을 spectrogram이라고 말합니다.

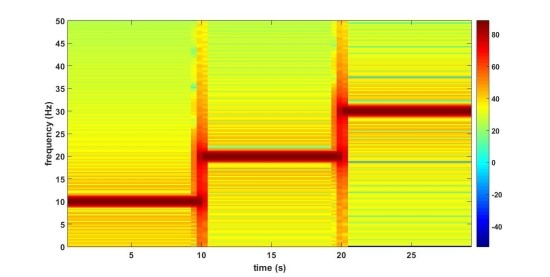
이러한 STFT에도 단점이 있는데, 초기 신호를 window length에 따라서 분리시키기 때문에 푸리에 변환에 사용되는 신호의 길이를 감소시킵니다. 이에 따라 주파수 Resolution이 악화됩니다. 그렇다고 Window length를 증가시켜 Resolution을 향상시키면, 시간에 대한 Resolution은 악화됩니다. 이러한 주파수와 시간의 trade off 관계로 인한 Resolution의 한계를 완화시키기 위한 방법이 Overlap 입니다. (여기서 말하는 주파수 해상도란 원하는 신호를 주파수 domain에서 관찰할 때 얼마나 촘촘한 간격으로 해당 주파수 대역의 값을 관찰 할 수 있는가를 말합니다. (주파수 해상도 참고 https://angeloyeo.github.io/2019/10/12/Frequency_Resolution.html)

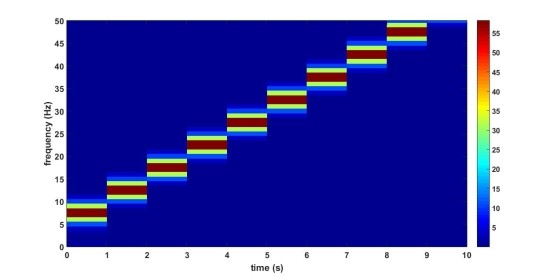
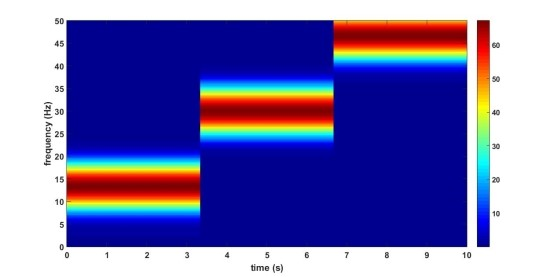
위의 그림들은 5Hz에서 50Hz까지 주파수가 일정하는 증가하는 신호에 대해서 window length를 1초(위 첫번째 그림), 3.3초(아래 두번째 그림)로 STFT 분석한 것입니다. 같은 신호임에도 window length에 따라 표현이 달라지는 것을 확인할 수 있는데, window length가 작을 경우 시간에 대한 Resolution은 좋지만 주파수 Resolution은 단순한 것을 확인할 수 있습니다. window length가 큰 경우, 시간 Resolution이 단순하지만 주파수 Resolution은 좀더 세밀한 것을 확인할 수 있습니다.

만약 window를 overlap하면 어떻게 될까요?

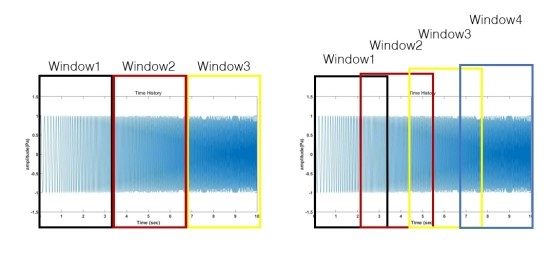
위의 그림의 왼쪽은 overlap하지 않았고, 오른쪽은 overlap 하였습니다. 그림과 같이 overlap을 적용하면 window가 서로 겹쳐짐으로 인해 더 많은 window가 적용되고 이에 따라 시간에 대한 Resolution이 좋아지게 됩니다. 아래의 그래프는 window length가 3.3초인 것에 overlap 70%를 적용한 것입니다. 적용하지 않았던 것과 비교하면 Time resolution이 확실하게 좋아진 것을 확인할 수 있습니다. 일반적으로 overlap은 50~ 75%로 적용한다고 합니다.

4. Feature Extraction

이제 푸리에 변환까지 이해했으니, 본격적으로 오디오 데이터에서 중요한 feature를 뽑아보도록 합시다. 가장 대표적인 feature로 MFCC (Mel-Frequency Cepstral Coefficient)가 있습니다. MFCC는 음성데이터를 특징벡터화 해주는 알고리즘인데, 머신러닝에서 어떠한 데이터를 벡터화 한다는 것은 학습이 가능하다는 의미이기 때문에 중요한 부분이라 말할 수 있습니다.

MFCC는 아래의 과정을 거쳐서 추출할 수 있습니다.

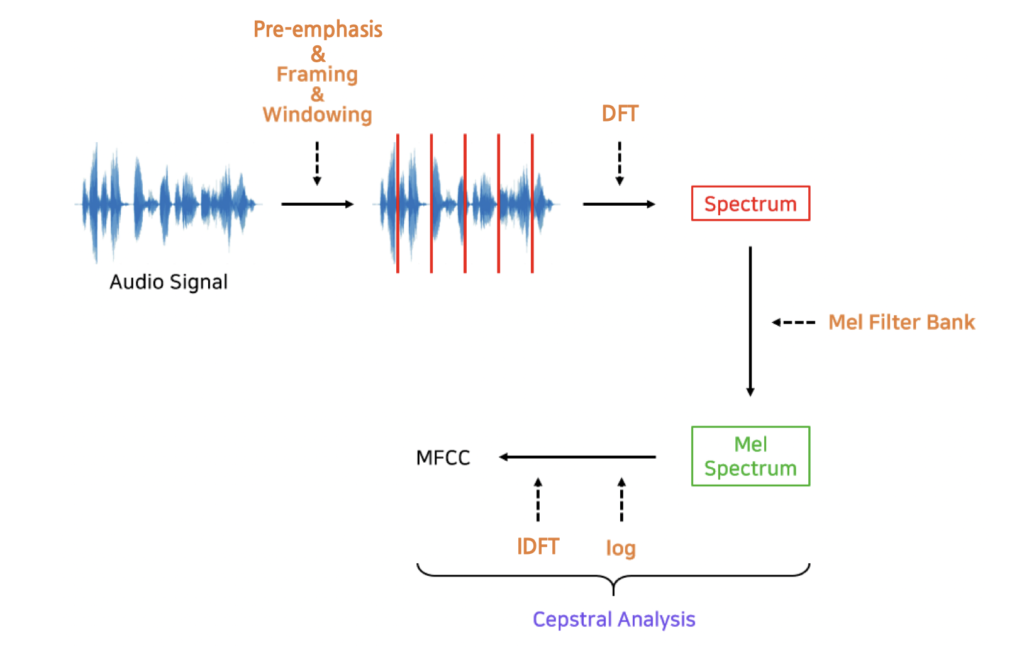
4.1 Pre-emphasis

사람의 말소리를 스펙트럼으로 변환해서 관찰하면 고주파보다 저주파 성분의 에너지가 더 많은 경향이 있다고 합니다. 아래 그림을 보면 대부분의 에너지가 스펙트럼 하단에 집중되어 있는 것을 관찰할 수 있습니다. 이러한 경향은 모음에서 자주 확인되는데, 고주파 성분의 에너지를 조금 올려주면 음성 인식 모델의 성능을 개선할 수 있다고 합니다. 고주파 성분의 에너지를 올려주는 전처리 과정을 pre-emphasis라고 합니다.

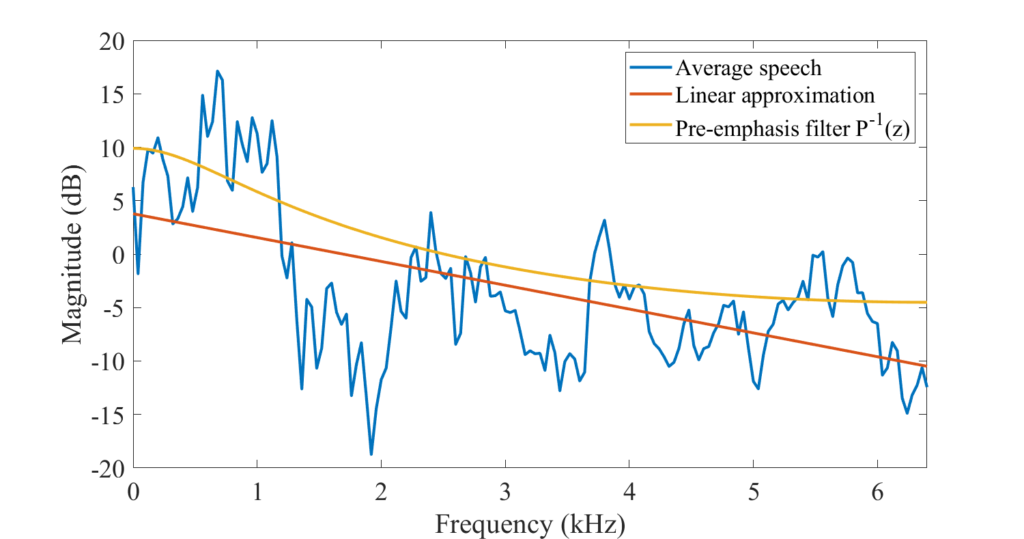
아래 그림을 통해 pre-emphasis filter(P(z) = 1 - 0.68z^{-1})가 어떻게 생겼는지 확인할 수 있습니다.

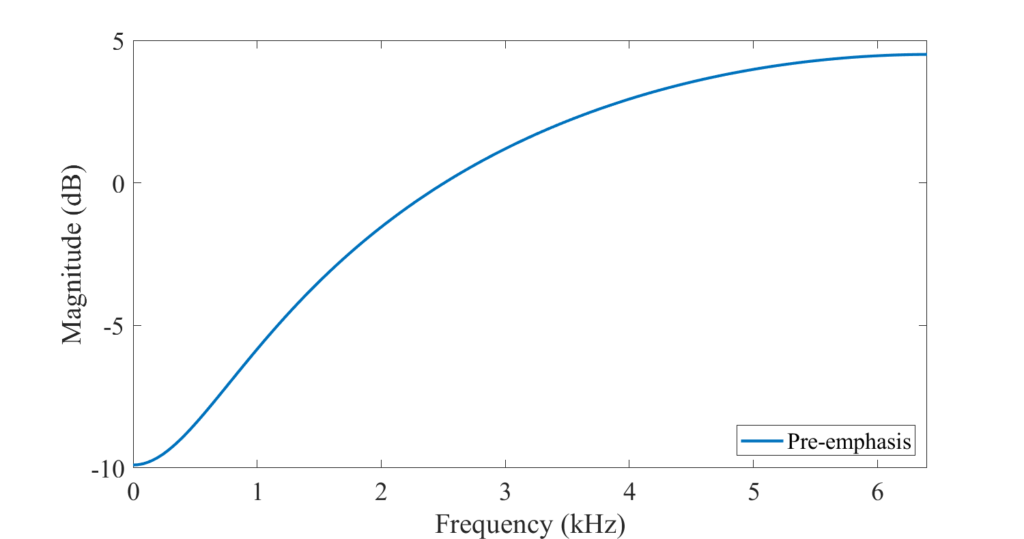
(그림 참고 https://wiki.aalto.fi/display/ITSP/Pre-emphasis)

4.2 Framing

음성 신호가 stationary하다고 가정해도 좋을 만큼 원시 음성 신호를 아주 짧은 시간 단위로 자르는 것을 framing이라고 합니다. 여기서 stationary는 ‘마치 지속적으로 울리는 사이렌 소리처럼 시점이 변하더라도 신호가 변하지 않는다’는 것을 의미합니다.

4.3 Windowing

앞에서 STFT를 설명하면서 잠깐 Windowing과 관련된 단어가 등장했는데, windowing은 각각의 프레임에 특정 함수(window function)를 적용해 경계를 스무딩하는 기법입니다. window function을 적용하면 깁스 현상(불연속을 포함하는 파형이 푸리에 합성되었을 때 불연속 값에서 나타나는 불일치 현상)을 방지할 수 있습니다.

window function에는 여러 종류가 있지만 그 중에 Hamming window를 가장 많이 사용합니다.

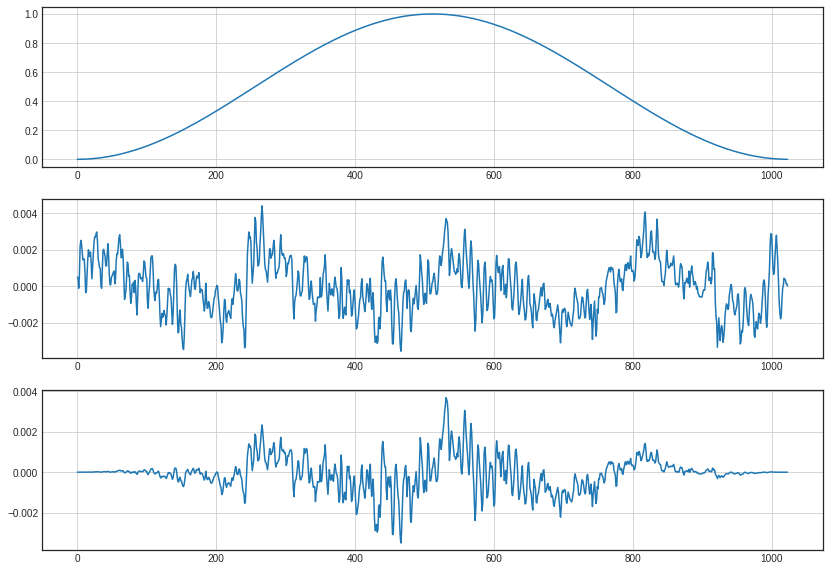
위의 그림을 보면 windowing을 적용하기 전 그래프의 끝부분이 다 다르지만, windowing을 지나고 나서 나오는 그래프는 끝이 0으로 일치한다는 특성을 볼 수 있습니다.

STFT에서 언급하였지만 다시 정리하면, window length/size는 time과 frequency의 resolutions를 제어합니다. short-window인 경우, frequency resolution이 낮고 time resolution이 높습니다. long-window인 경우, frequency resolution이 높고, time resolution이 낮습니다.

4.4 푸리에 변환

framing을 통해 나온 frame에 windowing을 적용하고 난 뒤에는 푸리에 변환을 해줍니다. 이때, FFT를 이용합니다. 푸리에 변환은 결정론적인 시계열 데이터를 주파수 영역으로 변환하는 것을 말하기 때문에 주파수 성분의 진폭(amplitude)과 위상(phase) 정보를 가지고 있습니다. 진폭은 주파수 성분의 크기를, 위상은 복소평변상 단위원상 위치를 나타낸다고 할 수 있습니다.

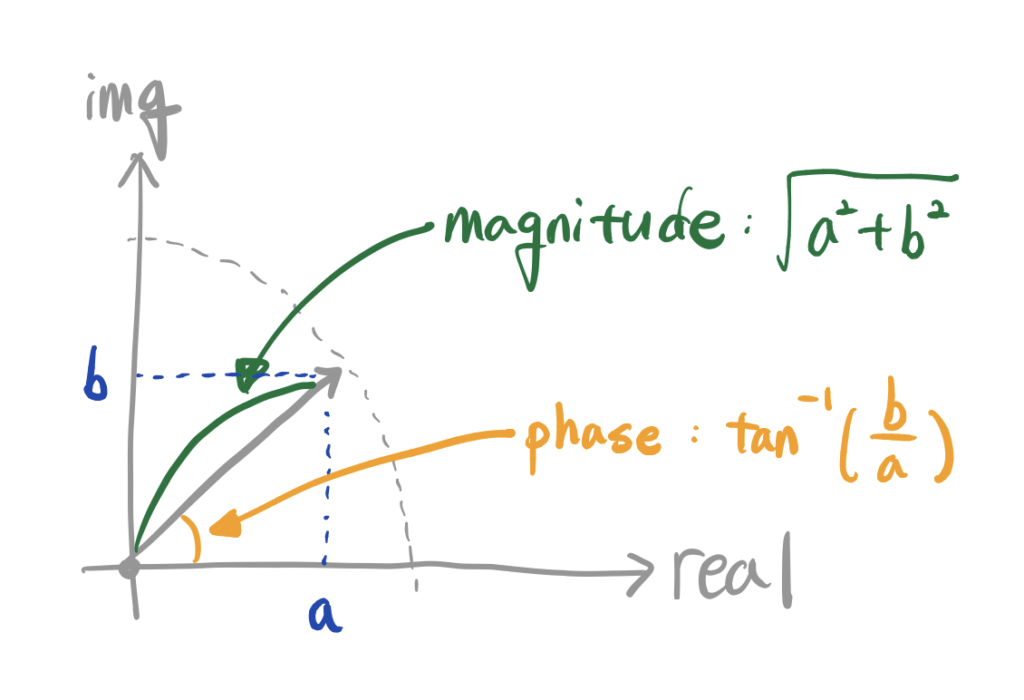
4.5 Spectrum & Power Spectrum

스펙트럼은 확률론적인 확률과정(random process) 모형을 주파수 영역으로 반환하는 것을 말하기 때문에 푸리에 변환과는 달리 시계열의 위상(phase) 정보를 가지고 있지 았습니다. 이 때문에 spectrum을 이용해 구하는 MFCC의 경우, 위상 정보를 활용하지 않습니다. ( 자세한 내용은 이 링크 참고 (추천) https://datascienceschool.net/03 machine learning/03.03.02 푸리에 변환과 스펙트럼.html#id7)

Power spectrum은 spectrum의 y축인 magnitude를 제곱해서 구할 수 있습니다.

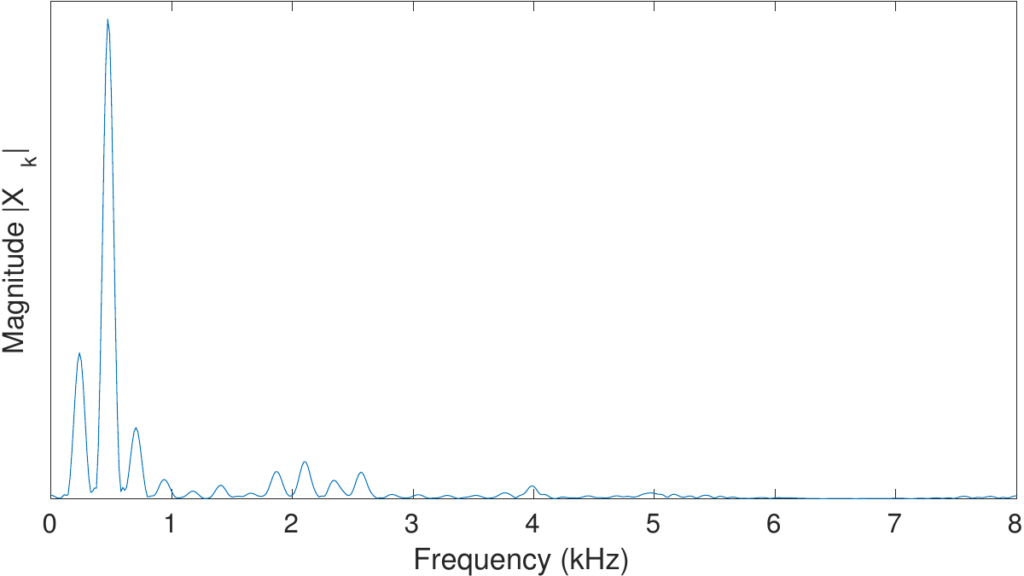
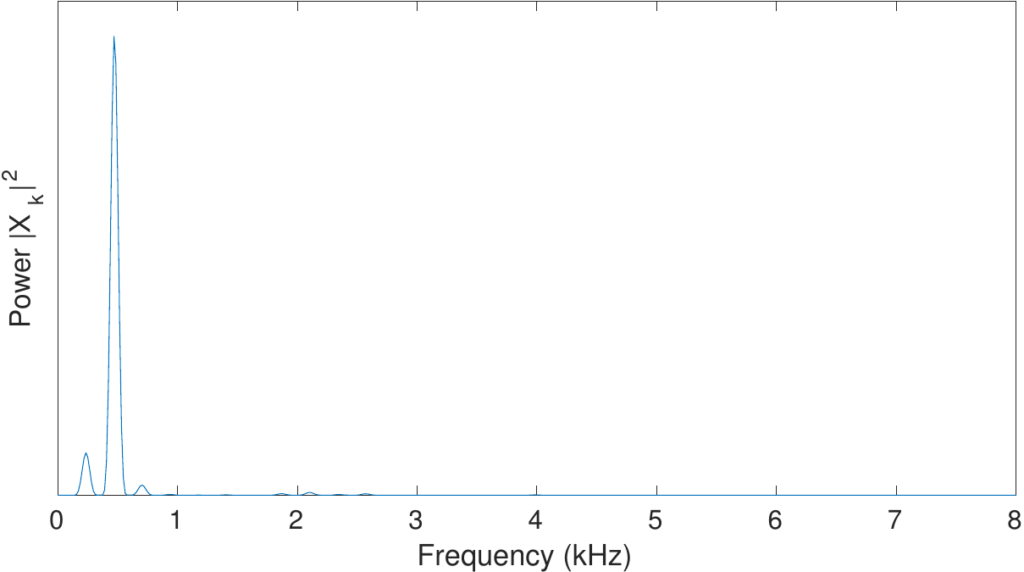
4.6 Mel Filter Bank

사람의 소리 인식은 1000Hz 이하의 저주파수 영역대가 고주파수 대비 민감하다고 합니다. 이 때문에 저주파수를 고주파수 영역대 대비 상대적으로 세밀하게 볼 필요가 있는데, 이때 적용하는 기법을 필터 뱅크 (filter banks)라고 합니다. 필터 뱅크는 멜 스케일 (mel scale) 필터를 사용합니다.

그러면 멜 스케일은 무엇일까요? mel-scale은 사람의 음을 인지하는 기준(threshold)을 반영한 scale 변환 함수 함수 입니다. 사람이 인지하는 음의 높낮이가 Hz와 linear한 관계가 아니라 exponential한 관계임을 이용하여 주파수를 바로 linear하게 다루지 말고, log함수를 통과시켜 mel scale로 바꾼 다음, linear하게 다룹니다.

아래와 같은 함수를 이용해 mel scale로 변환합니다. 멜 스케일읕 통해 기존 주파수 f를 멜(m)로 변환할 수 있습니다.

Mel(f)(혹은 m)= 2595log(1+\frac{f}{700})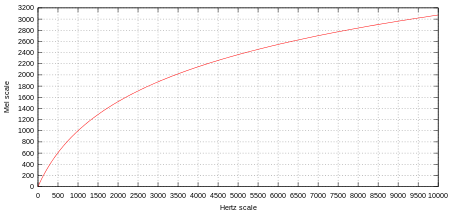

이제 멜 스케일을 알았으니 필터 뱅크로 돌아가봅시다.

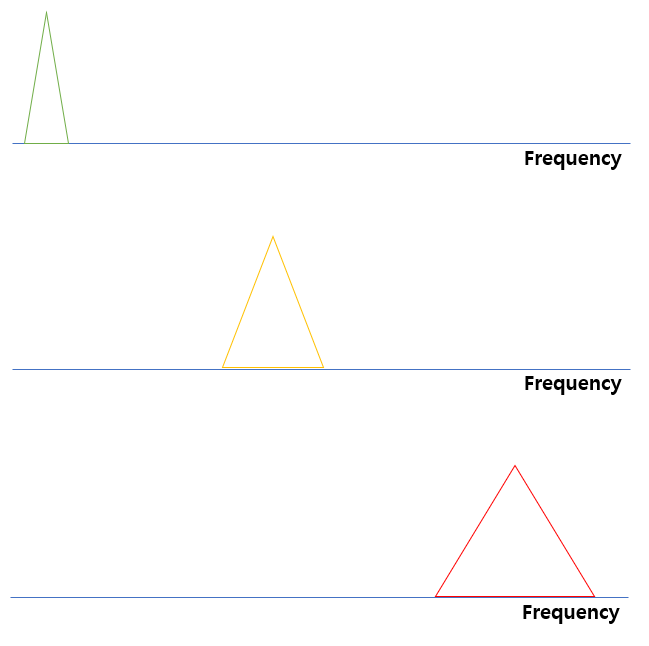
각각의 프레임에 대해 언어낸 주파수들에 대해서 m 값을 얻어내기 위해서 mel fiter를 적용하는데, 사람이 소리를 감지하는 특성을 이용하여 낮은 주파수에서는 작은 삼각형 filter를 가지고 고주파 대역으로 갈수록 넓은 삼각형 fiter를 가진다고 생각하면 됩니다.

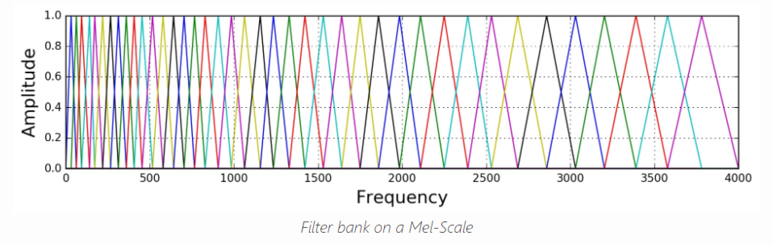
그래서 위와 같이 삼각형 필터 N개를 모두 적용한 필터를 Mel-filter bank라고 부릅니다.power spectrum이 위의 mel-fiter bank을 통과하게 되면 mel-spectrogram이라는 feature가 뽑히게 됩니다.

4.7 Log Mel Spectrogram

mel spectrogram에 log를 취해 log mel spectrogram을 구합니다.

(참고하면 좋음. 타대학교 랩실 세미나 자료 및 영상 시청 가능 http://dsba.korea.ac.kr/seminar/?mod=document&uid=254)

4.8 IDFT (or DCT)

멜 스케일 필터를 보면, 주변 몇 개의 헤르츠 기준 주파수 영역대 에너지를 한데 모아 보는 것을 확인할 수 있는데 이 때문에 멜 스펙트럼 또는 로그 멜 스펙트럼 feature 내 변수 간 상관관계가 존재하게 됩니다. 변수 간 상관관계를 해소하기 위해서 역푸리에 변환을 수행합니다. 로그 멜 스펙트럼에 역푸리에 변환을 실시하면 상관관계가 높았던 주파수 도메인 정보가 새로운 도메인으로 바뀌어 이전 대비 상대적으로 변수간 상관관계가 해소되게 됩니다.

여기서 역푸리에 변환 대신에 Discrete Cosine Transform을 행하기도 합니다. DCT는 특정 함수를 cosine 함수의 합으로 표현하는 변환을 말하는데, 이때 앞쪽(low) cosine 함수의 계수가 변환 전 데이터의 대부분의 정보를 가리고 있고 뒤쪽으로 갈수록 0에 근사해 데이터 압축의 효과를 보입니다. 즉, 낮은 주파수 쪽으로 에너지 집중 현상일 일어납니다.

4.9 MFCC

역푸리에 변환을 수행한 뒤 계수들 중에서 가장 저차원의 12개만 MFCC feature로 사용합니다. 이외 주파수 영역대 정보들은 만들 때마다 워낙 빠르게 바뀌어 음성 인식 시스템 성능 향상에 도움이 되지 않기 때문입니다.

딥러닝에서는 MFCC 대신 log mel spectrogram을 사용하기도 한다고 합니다.

---

이렇게 MFCC를 구하는 과정을 설명하면서 이제까지 공부한 것을 정리해봤습니다. 더 설명을 잘하고 싶은 부분도 있는데 더 구체적으로 적지 못한 부분이 있는것 같아 조금 아쉬움이 남습니다. 푸리에 변환과 관련하여 이해한 것을 더 적고 싶어 힘을 많이 썼더니 다른 부분에서 힘이 덜 들어간거 같아 아쉽습니다.

위의 내용보다 더 자세히 알고 싶다면, 제가 중간에 (추천)이라고 적어둔 링크를 확인하시면 좋을 것 같습니다. 굉장히 정리가 잘 되어있습니다.

+) 음성 데이터에서 위상 정보가 왜 중요한지 찾아보았으나 이렇다 할 이유를 찾지 못했는데, ‘Utilization of Phase information for speech recognition(음성 인식에서 위상 정보의 활용)’ 논문을 발견하여 시간이 허락한다면 이 논문을 읽어 위상 정보를 어떻게 활용하는지 알아보고자 합니다. (https://www.kci.go.kr/kciportal/ci/sereArticleSearch/ciSereArtiView.kci?sereArticleSearchBean.artiId=ART002037127)

읽어주셔서 감사합니다.