Intro
본 논문의 task는 단안 영상을 입력으로 받아 깊이를 추정하는 task로 DepthAnything 시리즈나 marigold와 같은 foundation model에 관한 논문입니다. 저자들은 이상적인 Depth foundation 모델이 갖춰야 할 세 가지 필수 조건으로 1) 정확한 기하 구조(Geometry Accuracy), 2) 실제 물리적 크기 예측(Metric Prediction), 3) 세밀한 디테일 표현(Geometry Granularity)을 제시합니다 . 하지만 기존 모델들은 이 세 가지를 동시에 만족시키는 것이 어려웠는데, 특히 이 연구의 기반이 되는 mogev1 모델은 상대적인 형태(Affine-invariant geometry)는 매우 정확하게 추정하지만, 실제 스케일(Metric scale)을 알 수 없고 디테일이 뭉개진다는 결정적인 한계를 가지고 있었습니다 .
일반적으로, 단순히 깊이(Depth) 값을 실제 미터 단위로 직접 예측하려고 하면 초점 거리와 실제 거리의 모호성(Focal-distance ambiguity)으로 인하여 깊이 추정의 성능이 저하된다고 합니다 . 이를 해결하기 위해 저자들은 이 둘을 분리하는 전략을 택했습니다. 기존 MoGe V1이 잘하는 ‘형태(Affine-invariant point map)’ 예측 능력은 그대로 유지하되, 전체적인 크기를 결정하는 전역 스케일 인자(Global Scale Factor)만 별도로 예측하여 합치는 방식으로 접근하는 것이죠. 이 방식이 상대적인 기하학적 정확도를 해치지 않으면서도 정밀한 스케일 복원을 가능하게 한다고 합니다.
두번째로 고려해야할 사항은 학습에 사용되는 데이터입니다. 실제 데이터는 노이즈가 많고 경계선이 불완전하여 디테일 학습을 방해하고, 반대로 합성 데이터는 깔끔하지만 현실 세계의 다양성을 담지 못합니다 . Depth Anything V2나 Depth Pro 같은 최신 연구들은 합성 데이터에 의존하여 깊이 추정 결과의 선명함을 얻었지만, 그 대가로 기하학적 정확도(Accuracy)를 희생했습니다 . MoGe-2는 실제 데이터를 쓰되, 깨끗하게 닦아서 쓰자는 실용적인 접근법(Data Refinement)을 도입합니다. 합성 데이터로 학습된 모델을 이용해 실제 데이터의 오류를 걸러내고, 빈 곳을 채워 넣음으로써, 실제 데이터의 정확도와 합성 데이터의 선명함을 모두 챙겼다고 합니다.
결과적으로 MoGe-2는 방대한 양의 실제 및 합성 데이터셋으로 학습되어, 상대적 기하 정확도, 절대적 스케일 정확도, 세밀한 디테일 복원이라는 세 가지 목표를 동시에 달성할 수 있었다고 하네요.
Method
저자들은 MoGe-2의 기반이 되는 기존 MoGe 모델의 작동 원리와 그 한계점을 우선적으로 설명하는데, MoGeV1은 단일 이미지를 입력으로 받아 장면의 3차원 포인트 맵을 추정하는 모델입니다. 이때 예측되는 결과물은 절대적인 좌표가 아닌 아핀 불변(Affine-invariant) 포인트 맵으로, 모델이 예측한 형상이 실제 정답(Ground Truth)과 구조적으로는 동일하지만, 미지의 전역 스케일(Scale)과 이동(Shift) 값만큼의 차이를 가지고 있어 실제 물리적인 거리를 예측하지는 못함을 의미합니다.
이러한 아핀 불변의 특성을 지니게 되는 이유는 모델 학습 때 예측값과 실제 정답 사이의 오차를 줄이기 위해, 우선 예측된 포인트 맵에 최적의 스케일과 이동 값을 적용하여 정답과 정렬시켜서 학습을 시키게 됩니다. 이때 정렬을 위한 최적의 파라미터는 병렬 탐색 알고리즘에 기반한 ROE Solver을 통해 계산되며, 이후 정렬된 결과와 정답 간의 L1 손실(Loss)을 최소화하는 방향으로 학습이 진행됩니다 . 특히, 가까이 있는 물체의 기하 정보를 더 중요하게 다루기 위해 깊이의 역수를 가중치로 사용하기도 합니다.
또한, 단순히 전체적인 형태만 맞추는 것에 그치지 않고 국소적인 기하 정확도를 높이기 위해 멀티 스케일 감독(Multi-scale Supervision) 기법을 사용합니다. 이는 이미지 내의 국소적인 구형 영역(Spherical regions)들을 샘플링하고, 각 영역 내부에서도 앞서 설명한 정렬 및 손실 계산을 수행하여 세부적인 굴곡까지 학습하도록 유도하는 방식입니다.
이렇게 학습된 Moge는 선명한 깊이 맵을 추정할 수는 있지만 구조적으로 물리적인 크기(Metric Scale)를 예측할 수 없으며 실제 활용에 필요한 세밀한 디테일(Fine-grained details)을 복원하는 데도 부족함이 있습니다.
Metric Scale Estimation
그럼 이제 Mogev1의 relative depth 문제를 해결한 부분에 대해서 살펴보겠습니다. 저자들의 MogeV2의 framework은 아래 그림2와 같은데 DepthAnything 모델 시리즈와 유사하게 DINOViT를 백본으로 하고 컨볼루션 디코더를 사용하는 모습입니다. 다만 차이점은 relative depth를 예측하는 head와 mask를 예측하는 head 뿐만 아니라 metric depth 예측을 위한 MLP head도 함께하는 모습입니다.
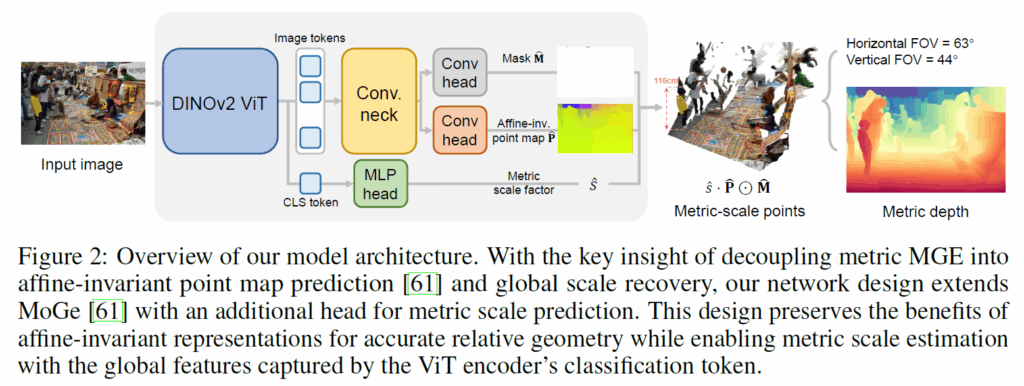
저자들의 그림2의 구조를 채택하기까지 이전에, 아래 그림3과 같이 scale estimation에 대하여 3가지 구조로 실험을 했다고 합니다.
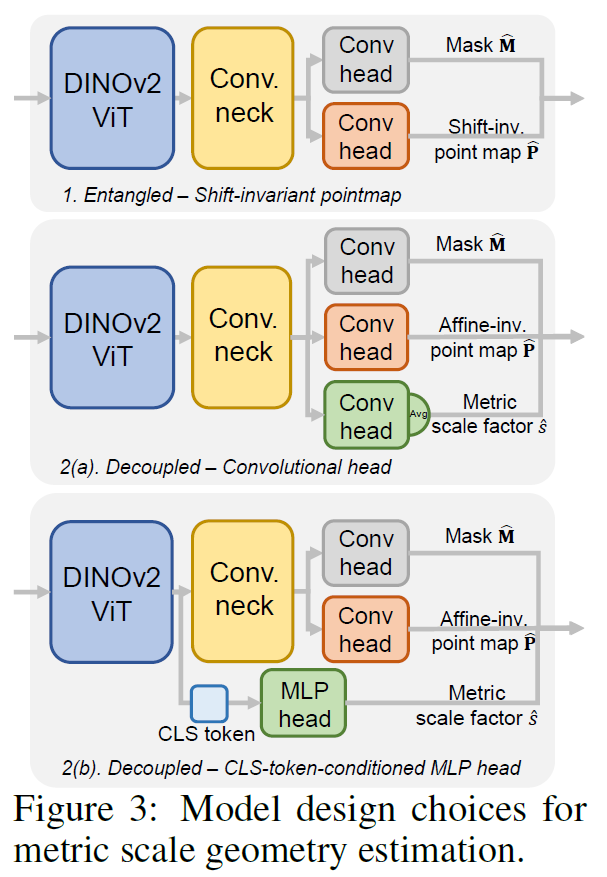
첫 번째 시도는 스케일 정보를 포인트 맵 자체에 포함시키는 ‘이동 불변(Shift-invariant) 예측’ 방식이었습니다. 하지만 이 방식은 실내와 실외를 아우르는 다양한 환경에서 예측값의 범위가 너무 넓어 학습이 불안정했고, 무엇보다 부정확한 스케일 예측이 발생시키는 큰 그래디언트가 기하학적 형태 학습까지 방해하는 치명적인 단점이 있었습니다 . 이러한 실패를 통해 저자들은 상대적인 기하 구조와 절대적인 스케일을 서로 간섭하지 않도록 완전히 분리(Decoupling)해야 한다는 결론에 도달했습니다. 즉, 기존 MoGe의 아핀 불변 포인트 맵 예측 경로는 그대로 유지하여 형태 정확도를 보장하고, 별도의 독립적인 경로를 추가하여 전역 스케일(Global Scale)만을 따로 예측하게 한 것입니다.
분리된 스케일 예측 모듈을 설계하는 과정은 그림3에 2(a)와 2(b)로 나뉩니다. 2(a)의 경우 일반적인 방식처럼 합성 곱(Convolutional) 헤드를 추가하여 공유된 특징 맵(Neck)에서 스케일을 뽑아내는 방식으로 해당 방식 역시 relative depth를 추정하는 부분과 metric scale을 예측하는 정보가 여전히 얽혀 있어(Entangled) 상대적 기하 정확도를 떨어뜨렸으며, 좁은 수용 영역(Receptive field) 탓에 전체적인 스케일을 파악하는 데 한계가 있었습니다 .
이에 대한 해결책으로 저자들은 CLS 토큰 기반의 MLP 헤드라는 매우 단순하고 직관적인 구조를 채택했습니다. DINOv2 인코더의 CLS 토큰에 담긴 풍부한 전역 정보를 직접 활용하여 스케일만 깔끔하게 예측해 내는 이 방식이, 결과적으로 기하학적 정밀함을 전혀 해치지 않으면서도 가장 정확한 스케일 추정 성능을 보여주었음을 확인했다고 합니다.
Real Data Refinement for Detail Recovery
저자들은 MoGe 모델이 미세한 구조를 제대로 복원하지 못하는 근본적인 원인을 실제 학습 데이터(Real-world Data)에 내재된 노이즈와 불완전성 때문이라고 판단하였습니다. LiDAR나 SfM(Structure from Motion)으로 얻은 실제 데이터는 센서 동기화 문제로 인해 색상 이미지와 깊이 정보가 어긋나거나(Mismatch), 반사되는 표면 등의 깊이 정보가 누락되는 경우가 빈번하기 때문입니다.
DepthAnythingv2와 같은 이전 연구들은 이를 회피하기 위해 깔끔한 합성 데이터(Synthetic Data)에 의존하기도 했으나, 이는 현실 세계의 복잡성을 담지 못해 기하학적 정확도가 떨어지는 딜레마가 있었습니다. 이에 저자들은 실제 데이터를 주력으로 사용하되, 합성 데이터의 선명함을 빌려와 실제 데이터의 오류를 수정하는 상호 보완적인 정제 전략을 제안합니다.
이 정제 과정의 첫 단계는 오류 필터링(Mismatch Filtering)입니다. 저자들은 DepthAnythingV2처럼 합성 데이터로만 학습된 모델(G_{syn})을 일종의 ‘참조 교사’로 활용했습니다. 하지만 G_{syn}이 예측한 절대적인 깊이 값은 실제와 다를 수 있으므로, 저자들은 전역적인 비교 대신 국소적(Local) 비교 방식을 채택했습니다.
즉, 이미지 내의 작은 영역마다 실제 데이터 포인트와 G_{syn}의 예측값을 정렬해 보고, 그 형태가 서로 크게 어긋나는 지점들을 센서 오류로 간주하여 과감히 제거하는 것입니다. 이를 통해 전역적인 스케일 편향 문제는 피하면서도 경계면의 부정합 같은 미세한 오류만 정밀하게 걸러낼 수 있었습니다.
필터링 후 구멍이 뚫린 영역이나 원래 데이터가 없던 부분은 ‘Geometry Completion’ 단계에서 채워집니다. 여기서 저자들은 로그 공간에서의 Poisson completion 기법을 적용했습니다. 이는 비어있는 영역의 ‘형태(Gradient)’는 선명한 $G_{syn}$의 예측값을 따르도록 하되, 그 ‘수치(Value)’는 주변에 남아있는 신뢰할 수 있는 실제 데이터 값에 부드럽게 이어지도록 경계 조건을 설정하여 채워 넣는 방식이라고 하네요. 결과적으로 이렇게 정제된 데이터는 실제 데이터가 가진 정확한 물리적 깊이 정보를 유지하면서도, 합성 데이터 수준의 날카롭고 선명한 디테일까지 갖추게 되어 MoGe-2의 성능을 극대화시킬 수 있었다고 합니다.

위의 그림은 깊이 결과 필터링 방식으로 기존의 RawGT에서 얇고 가는 객체라던지, 전경과 배경이 마주하는 테두리 영역 등에서 부정확한 GT 결과값이 생기는 여러 문제점들을 어느정도 완화해주는 모습을 보여주고 있습니다.
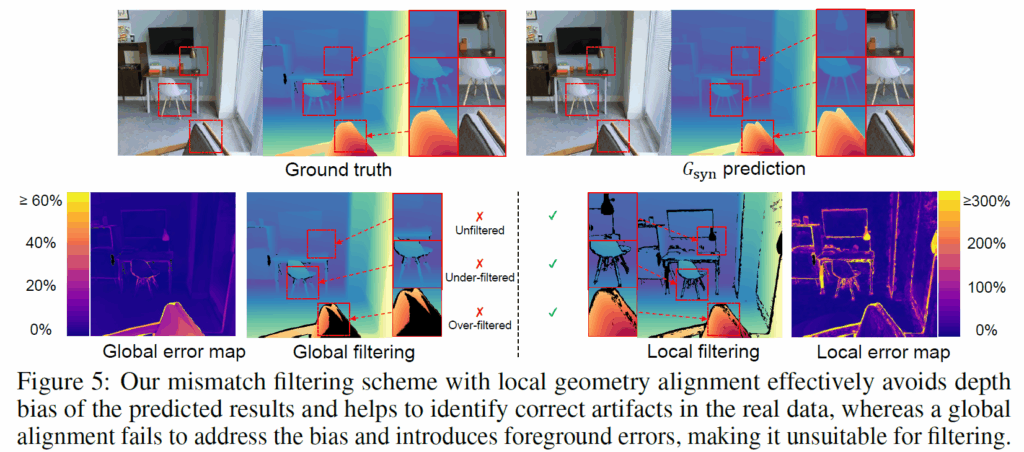
그리고 지금 그림의 경우에는 아까 소개드린대로 합성데이터로 사전에 학습된 모델이 real data에 곧바로 예측할 경우 해당 결과값의 metric scale이 부정확할 가능성이 높기 때문에 global error map을 구하는 것이 아닌 local error map을 구하기로 한 것의 예시를 의미합니다. 그리고 필터링 과정 자체도 global level로 할 경우 적절한 필터링을 수행하지 못하거나 너무 과한 필터링을 하지만, local 필터링의 경우에는 저자들 말로는 적절한 필터링이 이루어지고 있다고 합니다.
Experiments
실험 결과 소개하고 글 마무리 짓겠습니다.
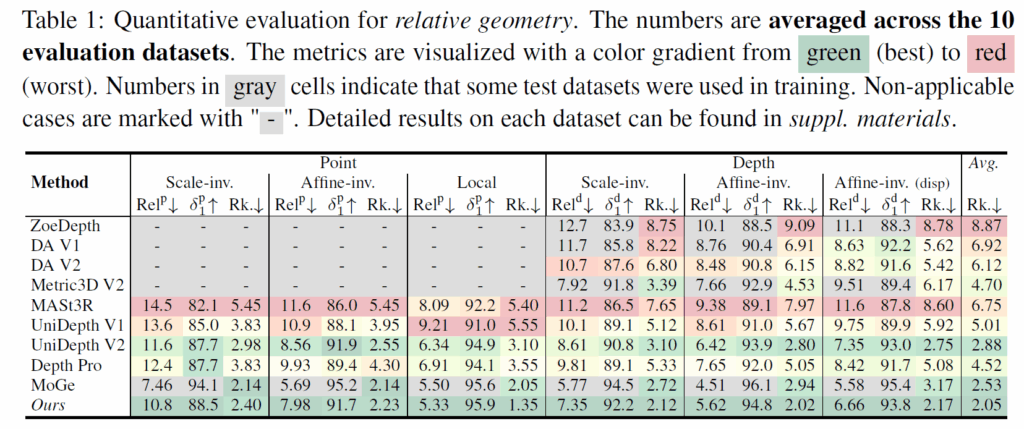
저자들은 모델의 범용성을 입증하기 위해 실내 상황(NYUv2, ScanNet++ 등), 주행 상황(KITTI, DDAD), 사물(GSO), 합성 데이터(Sintel, Spring) 등 다양한 도메인을 아우르는 총 10개의 데이터셋에서 평가를 진행했습니다.
표1은 relative geometry에 대한 실험으로 해당 실험의 주 평가 목적은 스케일을 예측하려다 원래 잘하던 형태(Shape) 추정 능력을 잃어버리지는 않았는지에 대한 것입니다. 이를 위해 저자들은 스케일 불변(Scale-invariant) 및 아핀 불변(Affine-invariant) 지표를 사용하여 형태적 유사성을 측정했습니다. 그 결과, MoGe-2는 모든 베이스라인 모델을 능가했을 뿐만 아니라, 상대적 기하 추정 분야의 SOTA인 기존 MoGe 모델과 동등한 수준의 정확도를 유지했습니다. 이는 스케일과 형태를 분리한 설계가 형태적 정확도를 크게 희생하지 않음을 의미한다고 볼 수 있겠습니다.
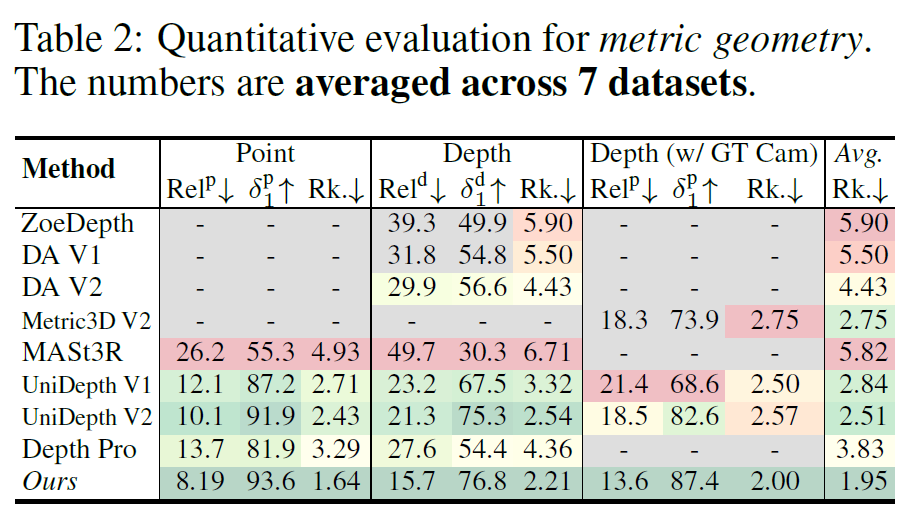
다음은 metric scale을 얼만큼 잘 예측하는지에 대한 실험으로, 평가 결과 MoGeV2는 상대적 포인트 에러(Rel_point)와 깊이 에러(Rel_depth) 등 모든 지표에서 기존 방법들과의 큰 격차를 보여줍니다. 특히 단순한 깊이 추정을 넘어, 카메라 내부 파라미터(Intrinsics)가 GT로 제공되지 않는 경우에서도 기존 연구들 대비 높은 성능을 보여준다는 점에서 긍정적으로 보여집니다.
Ablation Study
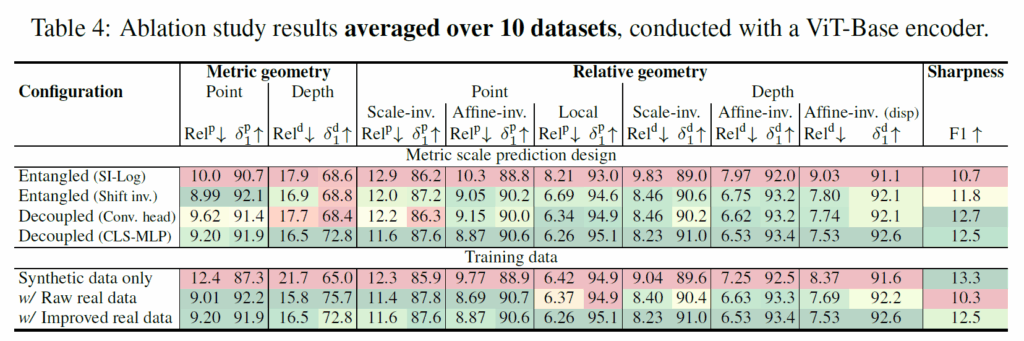
다음은 ablation study 관련 실험입니다. 먼저, 물리적 스케일(Metric Scale)을 예측하는 가장 좋은 방법을 찾기 위해 여러 구조를 비교했는데, 스케일과 형태 정보를 하나의 포인트 맵에 섞어서 학습하는 ‘결합(Entangled)’ 방식이나, 아핀 불변성을 유지하더라도 합성곱(Convolutional) 헤드를 통해 스케일을 예측하는 방식은 보다 저자들이 최종 채택한 ‘분리된 MLP 헤드(Decoupled MLP)’ 방식이 가장 우수한 성과를 보였습니다.
이는 기하학적 형태(Relative Geometry) 학습과 스케일 학습을 서로 방해하지 않도록 완전히 분리하는 것이 중요하며, 특히 이미지 전체의 정보를 담고 있는 CLS 토큰을 활용하는 것이 국소적 정보만 보는 합성곱 방식보다 ‘전역적인 크기(Global Scale)’를 파악하는 데 훨씬 유리하다는 것을 시사합니다 .
다음으로, 제안된 데이터 정제 파이프라인의 효과를 확인하기 위해 학습 데이터 구성을 달리하여 실험했습니다. 합성 데이터만 사용(Synthetic only)한 경우 예상대로 경계면의 선명도(Sharpness)는 가장 높았지만, 현실 세계와의 괴리(Domain Gap)로 인해 기하학적 정확도는 현저히 낮았습니다.
두번째로, 가공되지 않은 실제 데이터 사용(Raw real data)를 사용하는 경우 기하학적 정확도는 크게 향상되었으나, 데이터 자체의 노이즈로 인해 결과물의 선명도가 떨어졌습니다. 최종적으로, 저자들의 정제 과정을 거친 데이터를 사용했을 때(improved real data), 가공 전 데이터 수준의 높은 기하학적 정확도를 유지하면서도 합성 데이터에 버금가는 선명도를 달성할 수 있었습니다.
아래 정성적 결과를 끝으로 리뷰 마치겠습니다.
