[NeurIPS2024] Benchmarking LLMs via Uncertainty Quantification

본 논문은 LLM을 불확실성 측면에서 평가하는 벤치마크를 제시하는 논문입니다.

벤치마크의 필요성

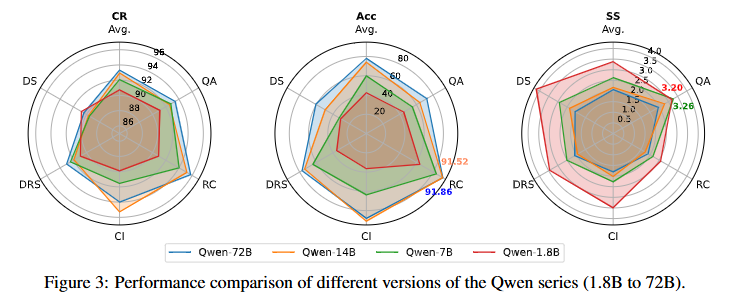
기존의 벤치마크는 LLM을 평가할때 예측의 정확도를 주로 리포팅했습니다. 그러나 논문에서 확인한 결과, 예측의 정확도와 모델의 불확실성은 서로 대체 불가능한 지표라고 합니다. Figure3은 이를 확인할 수 있는 실험 결과입니다. 이는 Qwen 모델의 사이즈별 성능을 MCQA 데이터셋의 테스크 별(QA, RC, CI, DRS, DS, All)리포팅 한 것인데요, 가운데의 ACC가 기본적으로 벤치마크에서 리포팅하는 모델의 정확도 지표입니다. 예상할 수 있는 대로 모델의 사이즈가 커질수록 (붉은색1.8B->파란색72B) 성능이 일관되게 개선됨을 확인할 수 있습니다. 한편 불확실성 지표인 SS의 경우 QA 테스크에서 모델 사이즈가 작은 Qwen 1.8B 모델보다 Qwen 7B의 불확실성이 큰 것을 확인할 수 있습니다. 즉 모델의 불확실성이 정확도와 항상 일관되지 않음을 통해 두 지표를 별개로 벤치마킹 해야함을 알 수 있습니다.

불확실성 측정 이론

논문에서는 기존의 불확실성 정량화 기법인 CP(Conformal Prediction, 정합예)를 LLM 평가에 도입하는 방법을 소개합니다. CP란 확률의 신뢰구간과 유사한 개념으로, softmax와 같은 예측에 대한 점수를 신뢰가능한 확률로 보정하는 기법입니다. 즉, 모델의 예측값들을 통해 prediction set을 만들고, 그 집합이 정답을 포함할 확률(coverage)를 보장하는 기법입니다. 즉 단일 확률은 정확한지 알 수 없지만, set을 통해 구축한 신뢰구간은 신뢰할 수 있는 확률적 기법이라고 이해하면 됩니다.

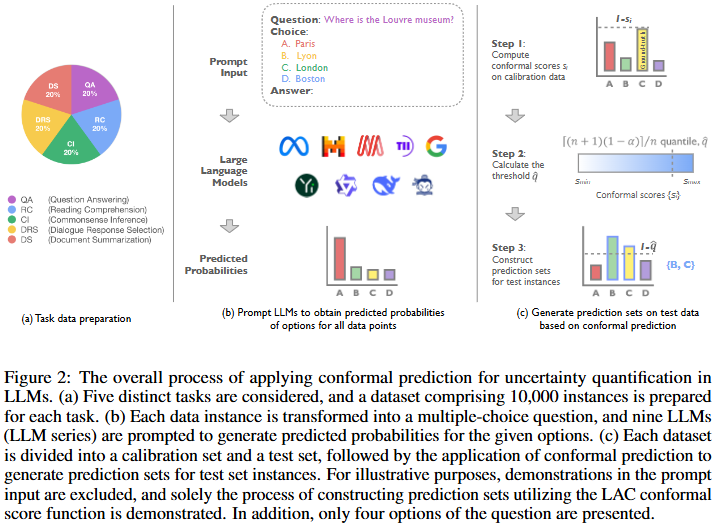
CP 기법은 Figure2와 같습니다. (b)와 같이 LLM 모델을 통해 예측을 생성합니다. 이후 이 예측들을 (c)와 같이 보정하는 것 입니다. 실제 변환 기법이 있는 부분은 (c)이므로 해당 부분을 위주로 설명하면 아래와 같습니다.

먼저 (b) 프로세스로 생성한 각 예측에 대해 score function으로 점수를 계산합니다. score fuction으로는 APS(Adaptive Prediction Sets)를 이용했는데, 수식은 아래와 같이 간단합니다. 정답인 X의 Y’ 라벨의 예측 확신도보다 높은 score를 모두 합산하는 방식으로 A: 0.5 B: 0.3 C: 0.2 로 예측했을 때, 정답이 B라면 0.5 + 0.3 = 0.8 이 됩니다. score가 클수록 잘못된 예측이 많은 것입니다.

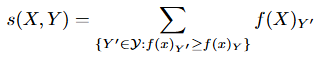
이후, 위와같이 score로 변환한 인스턴스별 점수에 대해서 신뢰도 (1-α) 분위수 값(=(n+1)(1-α)/n)으로 calibration 합니다. 즉, 신뢰구간을 이용하여 예측 중에서 α 보다 신뢰도가 낮은 예측을 없애는 것입니다. (n은 샘플의 갯수, α는 사용자 지정값)

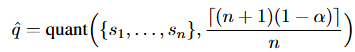
즉, 분위수 q^보다 작은 score에 해당하는 샘플로 prediction set(C(x_t))를 구성하게 됩니다.

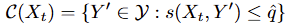
불확실성 측정 지표

논문에서는 CP를 활용하여 불확실성을 측정하는 지표인 SS(Set Size)를 제안합니다. CP가 생성한 prediction set의 크기가 SS입니다. 즉, 직관적으로 이해하면 모델이 불확실할수록 예측의 분산이 커져 SS가 높아지는 것 입니다.

(수식의 직관적 이해: SS는 전체 테스트 데이터셋(D_test)에 대하여 CP 사이즈의 평균)

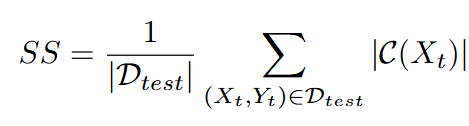
벤치마크

논문에서는 위에서 도입한 SS지표와 모델의 정확도(Acc) 그리고 불확실성 스코어(SS)의 신뢰 가능정도(모델 예측에 실제 정답이 포함되는 정도)를 나타내는 CR(coverage rate)를 리포팅하였습니다. 논문에서는 CP 정의 시 α를 0.1로 세팅하였고, CR 점수가 90%로 보장되어 통계적으로 신뢰가능한 지표임을 알 수 있습니다. 아래는 CR를 계산하는 방법으로 해당 수치가 전체 테스트 데이터셋(D_test)에 prediction set(C_(X_t))에 GT(Y_t)가 포함될 확률을 의미함을 알 수 있습니다.

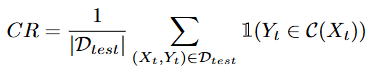
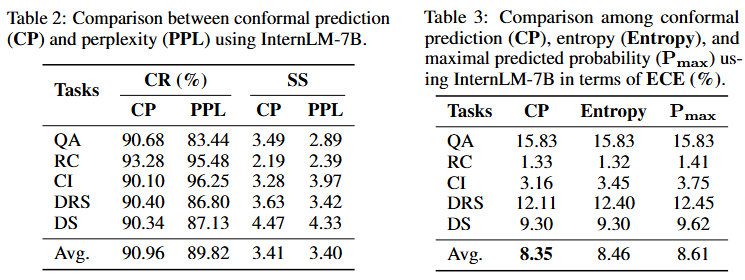
아래는 메인실험의 결과입니다. 실험은 대표적인 NLP 분야의 QA벤치마크인 MCQA(Multiple-Choice Question Answering)에 대해 진행되었으며 CR는 모두 90%이상이거나 그에 매우 가깝게 리포팅되었음을 먼저 확인할 수 있습니다. 또한 ACC와 SS에 대하여, 앞서 Figure3에서 검토하였듯이 두 지표의 관련성이 완전하지는 않고 상호보완되는 지표임을 확인할 수 있습니다. 예를 들어 DRS 테스크에서 MPT-7B와 InternLM-7B의 경우 ACC는 , InternLM-7B가 높으나 SS 지표에서는 그렇지 못함을 확인할 수 있습니다.

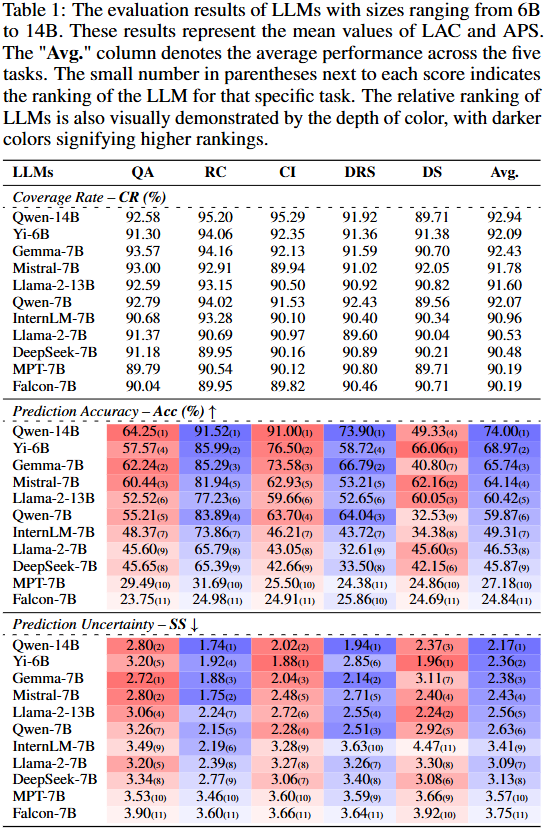
위에서 SS 지표가 ACC와 상호보완 지표임을 위의 메인 실험으로 확인했습니다. 즉 ACC가 높다고 불확실성이 낮음을 보장할 수 없었습니다. 다음으로는 모델의 scale에 따른 불확실성 정도를 확인했으며, 이는 위의 Figure3의 실험에 해당합니다. Qwen 모델을 위주로 실험하였으며, 모델이 클수록 ACC는 일관되게 높았으나, SS 수치의 경우 모델의 크기가 크다고 언제나 uncertainty가 낮지는 않았음을 확인할 수 있었습니다. 이처럼 독립적인 uncertainty benchmark의 필요성을 보이는 결과는 Qwen모델 뿐 만아니라 Llama-2 시리즈, Yi 시리즈, DeepSeek 시리즈, Falcon 시리즈에서도 동일한 경향을 보였으며 부록에 추가적으로 리포팅되어 있습니다.

다음 실험에서는 SS 지표가 다른 불확실성 지표 대비의 우수성을 보였습니다. 아래는 기존의 uncertainty 지표와 제안한 지표를 비교한 것입니다. 가장 일반적으로 사용되는 지표는 예측의 logit을 기반으로 정의된 entropy 지표입니다. 이는 logit의 분산을 수치화한 것으로 정답분포를 고려하지 않는다는 한계가 있습니다. 그러나 CP의 경우 분위수를 기반으로 정답 분포를 고려하여 신뢰도 높은 지표라고 볼 수 있습니다. 이론적으로 우수할 뿐 만 아니라 실험적으로도 기존 지표대비 우수성을 보였는데, 내용은 아래와 같습니다.

먼저 Table 2는 CR 측면에서 기존 지표인 PPL과 제안 방법(CP)을 비교한 것입니다. 이때 PPL은 entropy인 H를 기반으로 아래와 같이 정의되었습니다.

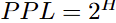
이때 모델이 예측에 강하게 확신하여 entropy가 0이라면 PPL은 1이 되고, 반대로 불확실성이 너무 높다면 entropy의 최댓값은 log2∣Y∣(모든 클래스에 대해 동일한 확률)입니다. 이때 PPL은 |Y|가 되므로 PPL의 범위는[1, |Y|]라고 할 수 있습니다. 이러한 특성으로 PPL의 수치를 CP와 동일하게 예측세트의 크기처럼 해석될 수 있는데, 즉 PPL이 클수록 불확실성이 크다고 해석될 수 있다는 것입니다. 이렇게 변환된 PPL과 CP 기반 불확실성 실험의 비교 결과 분위수를 통한 thresholding을 통해 거리가 너무 먼 예측을 제거하므로서 정답이 예측에 포함될 비율이 0.9 수준으로 보장되는 반면 기존 지표인 PPL의 경우 그렇지 못합니다. 따라서 APS를 활용해 CP 기반으로 측정한 score가 아닌 PPL을 통해 test set의 score를 활용하였을때의 CR은 CP 대비 낮습니다. (PPL로 계산한 SS를 기반으로 예측세트를 생성하는 등으로 CR을 측정할 수 있음)

다음으로 Table3는 PPL처럼 score의 대체로 활용할 수는 없지만, 기존에 언급되었던 불확실성 지표에 대해서 예측의 확률 분포와 실제 정답 분포사이의 거리인 ECE 스코어를 리포팅한 것입니다. 그 결과 CP가 가장 낮음을 통해 제안한 거리 산출법인 CP가 불확실성을 산출하기에 가장 적합함을 알 수 있습니다.

다음으로 free-form 생성에 대한 평가 결과입니다. 위의 기본적인 리포팅 방식은 classification 처럼 form이 지정된 예측에 대한 logit을 신뢰도 분위수인 CP로 보정하여 LLM의 능력을 평가했습니다. 이러한 산출 방식은 정답이 사실상 무한개인 free-form 형식의 예측에 평가를 할 수 없어 벤치마크로 활용되기에 취약하다고 평가될 수 있습니다. 이를 위해 논문에서는 free-form 생성에 대한 평가로 제안 방법을 확장한 벤치마크 역시 제시합니다. TriviaQA 데이터셋에 대한 실혐 결과로 질문당 20개의 정답을 생성한 후, PPL을 활용해 score를 산출합니다. 이때 free-form이기 때문에 분위수 설정이 불가능하여 Coverage 를 정확하게 보장하지는 못합니다. Table5의 CR 스코어가 기존 실험에 비해 낮은것으로 이를 확인할 수 있습니다. 그러에도 불구하고 free form에 대한 불확실성 평가가 가능은 하며 그 결과는 아래와 같습니다.

---

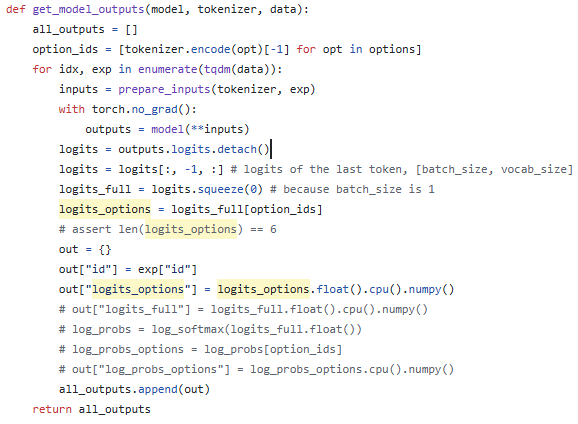
이상으로 리뷰를 마칩니다. uncertainty를 분석하는 방법이 없을까하여 읽게 되었습니다. 해당 방법은 예측의 logit을 활용하여 불확실성 정도를 수치화하는 방법이고 구현된 코드는 아래와 같습니다 open-source LLM의 출력에 logits을 추출할 수 있다는 것을 처음 알았네요.. 감사합니다 … ㅎㅎ