짧은 소개
본 논문은 LLM 답변의 불확실성을 수치화하기 위한 방법을 제시한 논문입니다. 특히 할루시네이션에 직접적인 영향을 미치는 지식부족형 불확실성을 수치화하는 기법을 제시하였으며, 수학적으로 증명할 수 있는 탄탄한 이론을 제시했습니다. 제안한 불확실성 수치화 방법은 기존의 방법보다 우수했음을 실험을 통해 증명하였습니다.
불확실성
모델 파라미터 뿐 만 아니라 데이터도 변수로 정의하는 베이지안 러닝에 따르면, 불확실성은 지식 부족에 의한 불확실성(epistemic uncertainty)과 랜덤성에 의한 불확실성(alcatoic uncertainty) 으로 나눌 수 있습니다. 기존 이론에 따르면 LLM의 할루시네이션을 유도하는 불확실성은 epistemic uncertainty 입니다. 그러나 일반적으로 두가지 불확실성이 구분되지 않은 딥러닝 모델에서 epistemic uncertainty 수치만 얻는것은 불가능에 가깝습니다. 본 논문은 직접적으로 이를 구하는 대신 대체가능한 하안을 제시하여 LLM의 답변을 이용하여 epistemic uncertainty만 수치화할 수 있는 메트릭을 제시합니다.
메인 아이디어
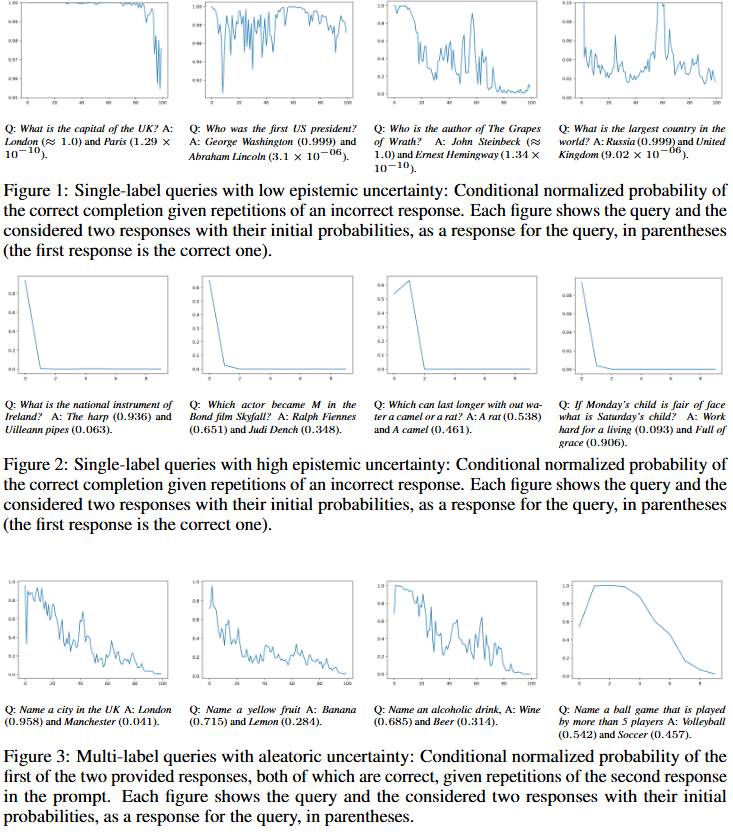
LLM의 응답을 이용하여 epistemic uncertainty만을 수치화하는데 관여한 메인 아이디어는 다음과 같습니다: 만약 모델이 답변에 확신한다면 질의에 대한 답변은 독립적일 것이다. 예를 들어 x=”영국의 수도는?”이라는 질의(x)에 대해 모델이 확신도가 높다면, 답변(y)은 “다른 답변 중 하나는 파리이다”라는 정보를 제공하여도 “영국의 수도는 런던이다”라는 응답에 대한 확신도가 높을것입니다. 이러한 아이디어가 실제로 동작한다는 것을 단적으로 보여주는 것은 위의 Figure1,2,3입니다.
먼저 Figure1은 epistimic uncertainty 즉, 할루시네이션 가능성이 낮은 상황에서의 결과를 보여줍니다. 가장 왼쪽의 첫번째 결과를 보면 “영국의 수도는?”이라는 질문과 함께 “다른 답변 중 하나는 파리이다”라는 다른 예측 결과를 x축의 개수만큼 반복하여 제공했을때 성능 하락 정도입니다. 그 결과 80회 이상 반복했을 때 100에서 95까지 약간의 성능 하락이 있었음을 확인할 수 있으며, 이전 예측에 대한 정보가 답변에 영향을 거의 미치지 않음을 알 수 있습니다. 한편 Figure2는 epistimic uncertainty가 높은 상황에서의 결과를 보여줍니다. 동일하게 가장 왼쪽의 예시를 보면 “아일랜드의 국가 악기는 무엇인가요?”라는 질의에 대해 틀린 응답인 Uilleann pipes를 반복하여 제공할 수록 정답인 The harp라고 답할 가능성이 빠르게 감소하여 0.0 까지 하락함을 확인할 수 있습니다. 즉, 할루시네이션 가능성이 높을때는 이전 답변에 대한 정보를 참조하지만, 할루시네이션 가능성이 낮을때에는 이전 답변에 대한 정보를 아무리 주어도 확신도가 높아 성능에 영향이 없다는 것입니다. 마지막으로 Figure3은 여러개의 정답이 있는경우로 aleatoric uncertainty가 높을 수 밖에 없는 상황에서도 이러한 아이디어가 동작하는지 확인할 수 있는 결과입니다. 가장 왼쪽의 결과를 보면 “영국의 도시는?”이라는 질문에 대한 동작을 보여줍니다. 즉, London과 Manchester가 복수정답인 상황입니다. 이러한 상황에서 “다른 답은 Manchester 이다”라는 프롬프트를 반복적으로 추가하였으나 Figure2와 같이 성능의 급격하게 하락하지는 않으며 100회 반복시 London으로 대답할 확률이 1에서 0까지 순차적으로 감소는 현상을 보였습니다. 해당 실험 결과를 통해 LLM이 Aleatoric uncertainty에 대해 분별할 수 있음을 알 수 있습니다. 즉, LLM의 응답의 분포를 변화를 통해 aleatoric uncertainty(변화가 미묘)와 구별된 epistimic uncertainty(변화가 급진적)를 수치화 할 수 있음을 알 수 있습니다.
이론 정립
논문은 실제로 할루시네이션을 위한 불확실성을 수치화하는 제안 메트릭(MI)를 고안하기 전에 이론적인 하안을 정의합니다. 먼저 epistimic uncertainty의 가장 정확한 산출법은 실제 정답 분포(P~)와 모델의 예측으로 얻은 pseudo joint distribution인 (Q~) 간의 분포 차(쿨백-라이블러 발산)인 아래 [eq.1]과 같습니다. 그러나 추론에서 질의에 대한 답변의 정답 분포(P~)를 알 수 없기에 이를 수치화하는것이 불가능했습니다.
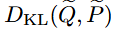
한편, 정답 분포(P~)와 예측(Q~)간의 분포 거리는 독립 분포로 곱 분포이며 아래와 같이 분해될 수 있습니다.
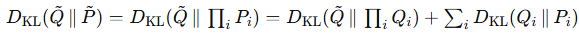
즉, 무한번 시행으로 얻은 예측 분포(Q~ⓧ)와 t시점의 예측 분포(Q~)간의 거리에 0 이상 작은 값인 Qi와 Pi 분포간의 추가 거리를 더한것입니다. 따라서 아래의 부등호[eq.3]를 만족합니다.
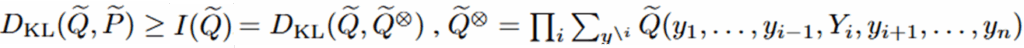
제안한 불확실성 산출 방법(Mutual Information, MI)
위의 수학적 정의를 통해 epistemic uncertainty의 대체가능한 근사치를 정의 했습니다. 그러나 근사치에 활용된 Q~ⓧ의 경우 무한번의 시행을 가정하기에 실제 산출식에 활용하기 어렵습니다. 본 논문에서는 이를 sampling 갯수(k개)를 통해 제한하며 pseudo-joint distribution(μⓧ)을 이용합니다. 전체적인 동작 방법은 위의 [Algorithm 1]과 같습니다.
산출식을 설명하면 아래와 같습니다. k번의 반복시행을 통해 sample tuples(M)을 생성합니다. i번째 응답과 전체 샘플(M)간의 분포 차이를 μ^ⓧ, i번째 추론의 정규화된 분포는 μ^ 입니다.(line4) MI는 이 두 수치를 통해 계산되는데, 두 수치가 0이 됨을 방지하기 위해 γ1,γ2를 정의하여 활용합니다. 두 보정 파라미터는 γ2>=γ1의 관계를 만족하는것이 일반적이지만 보통 1/k로 세팅되에 샘플링 표본의 수가 증가하면 0에 가까워집니다.
MI 지표 실험 결과
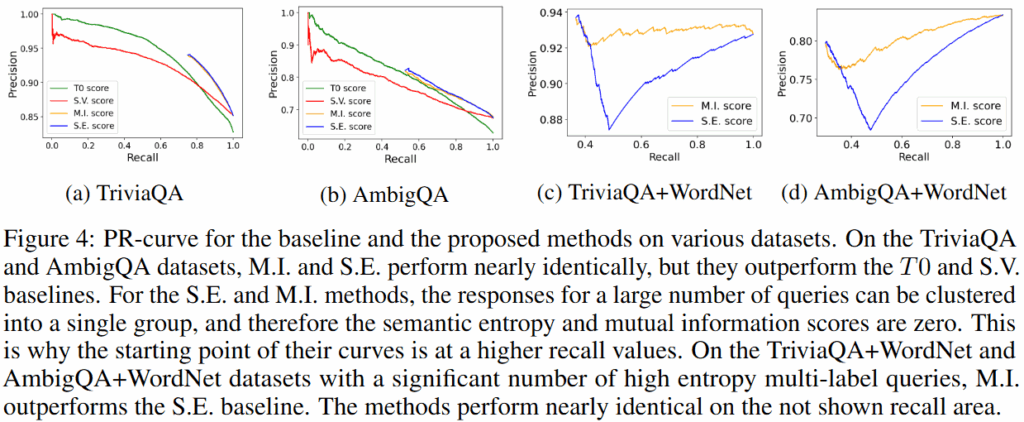
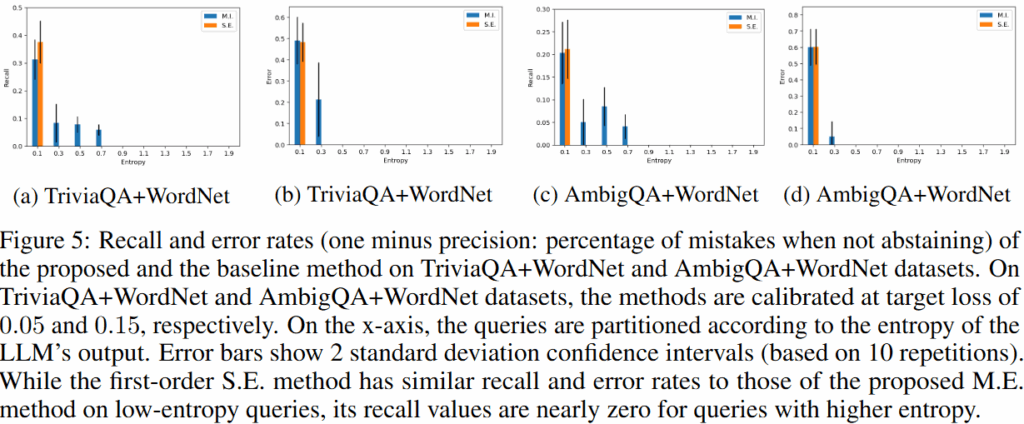
논문에서는 제안한 불확실성 산출 지표인 MI의 타당성을 보이기 위해 기존의 불확실성 수치화 기법과 비교하여 정확도를 리포팅했습니다. 실험은 Gemini 1.o Pro에 대해 메인으로 수행했으며, TriviaQA(단일 정답을 갖는 자연어 QA 데이터셋), AmbigQA(단일 정답을 갖는 자연어 QA 데이터셋), WordNet(어휘 데이터베이스)를 활용하여 실험데이터를 구성하였습니다. 단일 정답 중심 세팅(epistemic 성능, TriviaQA/AmbigQA)과 다중 정답 혼합 세팅(alcatoic, epistemic 구분성 검증, TriviaQA+WordNet/AmbigQA+WordNet)에서 실험을 수행했습니다. 또한 제안한 지표의 우수성을 보이기 위해 기존에 제안된 방법인 S.E.(Semantic-Entropy)/ S.V.(Self-verification)의 결과와 비교합니다.
실험 결과 단일정답중심에서는 제안한 방법이 T0, S.V.보다 우수하며 S.E.와 유사한 성능을 보였습니다. 단일 정답이기 때문에 S.E. 기법으로 충분히 불확실성을 감지할 수 있기 때문인데요, 한편 다중 정답 중심 세팅(Figure4/c,d & Figure5) 에서는 M.I. 기법이 S.E. 기법보다 높은 할루시네이션 감지율을 통해 직접적인 원인인 epistimic uncertainty만을 잘 수치화하였음을 보여주었습니다.
부록
본 논문은 부록에 수학적 증명과 다양한 추가실험이 제공되고 있습니다. 그 중 하나로 소형모델인 Gemini 1.0 Nano-1을 활용한 실험 결과 또한 리포팅 하고 있습니다. 실험 결과 위의 Figure4/5의 경향이 동일하게 나타남을 통해 제안한 아이디어가 유의미함을 한번 더 검증하고 있습니다.
정리
본 논문은 LLM의 응답의 분포를 활용해 할루시네이션을 감지할 수 있는 방법을 제시하였습니다. 특히, 할루시네이션 가능성이 높은 답변의 경우 기존 시행의 응답이 제시되면 추론 결과의 분포가 급격하게 변동한다는 점이 인상깊습니다. 다만, 추론에서 발생하는 비용이 있기때문에, 비디오 연구등에 적용하기 적합한지는 미지수네요. 수학적 정의의 일부 (전제조건)등은 편한 이해를 위해 일부 리뷰에서 생략하였으나 논문에서는 자세하게 논리적으로 다루고있습니다. 따라서 이론적으로 탄탄한 지표라는게 제안 방법론의 장점이라고 할 수 있겠습니다.이상으로 리뷰를 마치겠습니다. 감사합니다.
