오랜만에 엑스리뷰 작성 감 좀 잡을 겸 인턴 기간동안 읽었던 논문 한편을 가볍게 리뷰할까 합니다. ICRA 2025 에 게재된 HeLiOS 라고 하는 논문이며, 서울대 김아영 교수님 연구실에서 작성되었습니다.
해당 논문은 서로 다른 이종(Heterogeneous) 한 LiDAR 간의 place recognition 문제 해결에 초점을 둡니다. 우리가 흔히 생각하는 360도 FoV 를 가지는 3D LiDAR 말고도 스캐닝 방식, FoV 등등이 모두 다른데 이를 고려한 알고리즘 설계를 핵심으로 둡니다. 바로 리뷰 시작하겠습니다.
1. Introduction
로보틱스나 자율주행 분야에서 LiDAR를 이용한 장소 인식은 현재 위치를 이전에 방문했던 장소와 매칭하는 매우 중요한 기술입니다. 리뷰에선 줄여서 LPR 이라 칭하겠습니다 (LiDAR Place Recognition). 기존의 LPR 연구들은 대부분 360도 전체를 스캔하는 고가의 회전형(spinning) LiDAR에 초점을 맞춰왔습니다. 하지만 최근에는 가격이 저렴하고 형태가 다양한 고정형(solid-state) LiDAR 등 여러 종류의 LiDAR가 등장하면서, 서로 다른 종류의 LiDAR 센서로부터 얻은 데이터를 매칭해야 하는 필요성이 커지고 있습니다.
서로 다른 LiDAR는 FoV, 해상도, 스캐닝 패턴이 모두 다르기 때문에, 같은 장소에서 데이터를 취득했다고 한들 취득된 point cloud 분포는 완전히 다르게 나타납니다. 아래 그림을 보면 아시다시피, 동일 장소에서 서로 다른 FoV를 가지는 LiDAR 로 부터 취득된 두 point cloud 의 분포가 상이한 것을 확인할 수 있습니다.
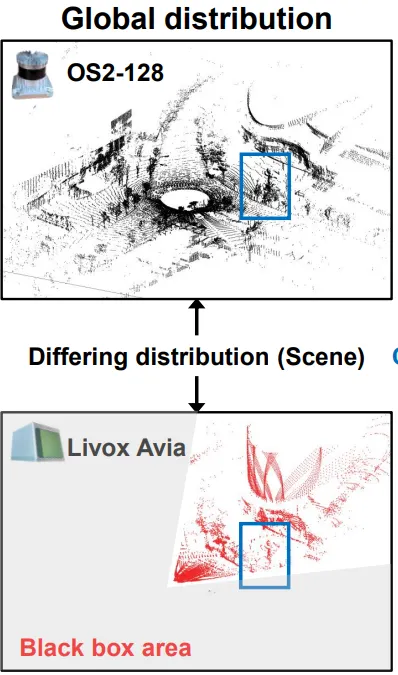
이렇게 서로 다른 분포에 대한 고려가 필요하지만 기존의 방법론들은 이에 대한 고려를 하고 있지 않습니다. 가령 일반적으로 LPR 분야에서는 triplet loss 기반 학습을 위해 현재 query 에 대해 positive 와 negative pairs 를 구성하게 되는데, 보통 일반적으로 데이터들 사이의 물리적인 거리 (meter) 를 기준으로 합니다. 예를들어 현재 query 와 5m 이내인 샘플은 positive로, 5m이상 10m이하인 샘플은 negative로 구성하는 방식이죠.
하지만 아래의 그림에서 볼 수 있듯이, 거리는 가깝지만 실제 겹치는 영역은 없는 경우(파란색-노란색 원)나, 거리는 멀지만 충분히 겹치는 영역이 있는 경우(검은색-노란색 원)가 발생할 수 있습니다. 그리고 이렇게 잘못 구성된 pair로 학습하면 모델의 성능에 악영향을 끼칠 수 밖에 없습니다.
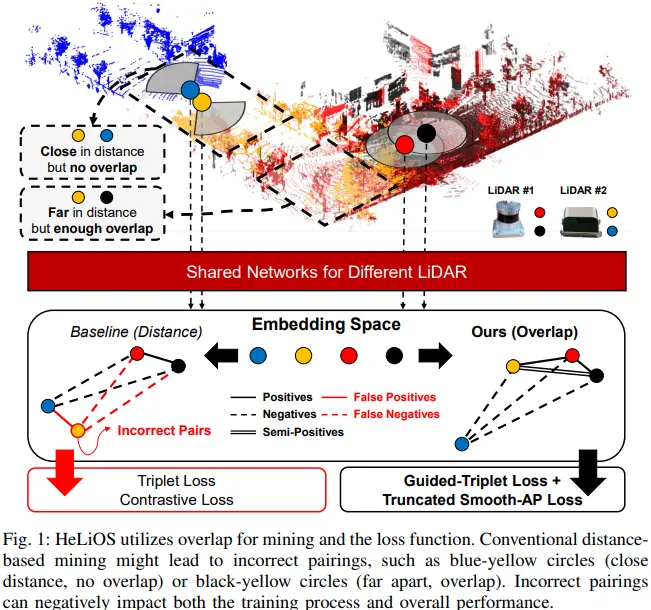
2. Method
본 논문은 이러한 문제를 해결하고자 이종 LiDAR 간의 place recognition 을 위한 모델인 HeLiOS 를 설계합니다.
2.1. Problem Definition
LPR의 목표는 N개의 3D 좌표(x, y, z)로 구성된 point cloud 데이터 P로 부터 global descriptor g 를 생성하는 것입니다. 이는 feature 추출 함수인 f(\cdot) 와, feature 를 집계 (aggregation) 하는 함수인 h(\cdot) 로 구성된 최종 매핑함수 \Omega=h(f(\cdot))를 통해 이루어집니다.
학습의 최종 목표는 이 매핑 함수 \Omega를 최적화하여, 실제 공간에서의 거리 관계가 임베딩 공간에서도 동일하게 유지되도록 하는 것입니다. 즉 실제 gps 기준으로 지도상에서 위치가 가까운 두 point clouds x_q와 x_i 의 global descriptor 간의 거리가, 위치가 멀리 있는 두 point clouds x_q와 x_j 의 global descriptor 간의 거리보다 가깝게 만드는 것을 목표로 합니다. 이를 d_{g}(g_{q},g_{i})<d_{g}(g_{q},g_{j}) 로 표기합니다.
2.2. Locality-aware Feature Extraction Network
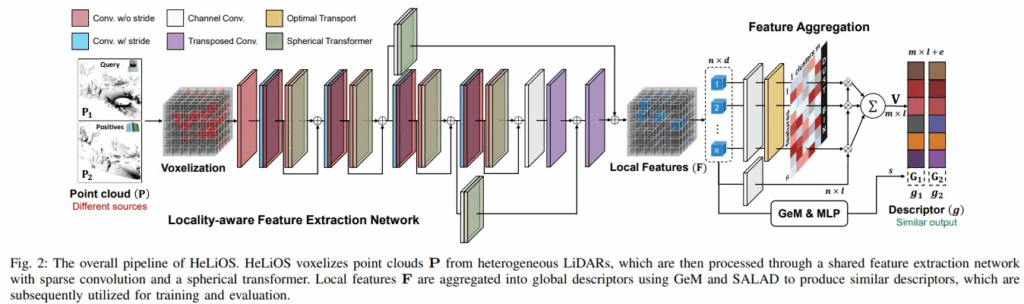
HeLiOS 의 모델 구조는 위 그림과 같습니다. HeLiOS 는 point clouds의 local feature 를 인코딩하기 위해 U-Net 구조와 sparse convolution 기반의 구조를 사용합니다. 여기서 sparse convolution 란, dense한 2d Image와 달리 sparse 한 3d lidar 를 효과적으로 인코딩하기 위해 설계된 방식이며, 모든 공간에 대해 convolution 연산을 하는 것이 아니라 point cloud 가 존재하는 영역에 대해서만 convolution 연산을 수행하는, 효율적인 연산 방식이라 생각하시면 됩니다.
아무튼 이를 사용해서 입력으로 들어온 point cloud 를 3d voxel 형태로 변환한 후 인코딩을 진행합니다. 하지만 이종 LiDAR 의 경우 스캔하는 패턴과 범위(FoV) 가 달라서 취득된 point cloud 데이터 분포가 매우 상이하기 때문에 학습이 많이 불안정해진다고 저자는 말합니다.
이 문제를 해결하기 위해, HeLiOS는 데이터의 전체적인 분포 대신 local 분포에 집중하도록 모델 구조를 살짝 변경합니다. 전체 point clouds 공간을 작은 spherical(구형 모양) window 와 cubic (정육면체 모양) window으로 나누고, 이 작은 window 내부의 복셀들에 대해서만 multi-head attention을 적용합니다. 서로 다른 LiDAR 데이터라도 작은 지역으로 쪼개서 보면 분포가 유사해지기 때문에, 트랜스포머가 효과적으로 특징을 학습할 수 있게 됩니다. 쉽게 생각해 전체 global attention 을 하는 것이 아니라, 작은 window 단위로 잘라서 local attention 을 수행했다~ 라고 생각하시면 됩니다. 또한, 네트워크의 깊은 층에서 downsampling 으로 인해 복셀 수가 점차적으로 줄어드는 문제에 대응하기 위해, sparse convolution이 적용될 때마다 spherical(구형 모양) window 의 크기를 점진적으로 1.5배씩 확장시킵니다.
아무튼 이렇게 global 단위가 아니라 local 한 단위로 이종 LiDAR 간의 point clouds 를 관찰하게 되면 유사한 분포를 관찰할 수 있게 됩니다. 이에 대한 시각 결과는 아래를 보시면 이해가 되실겁니다.
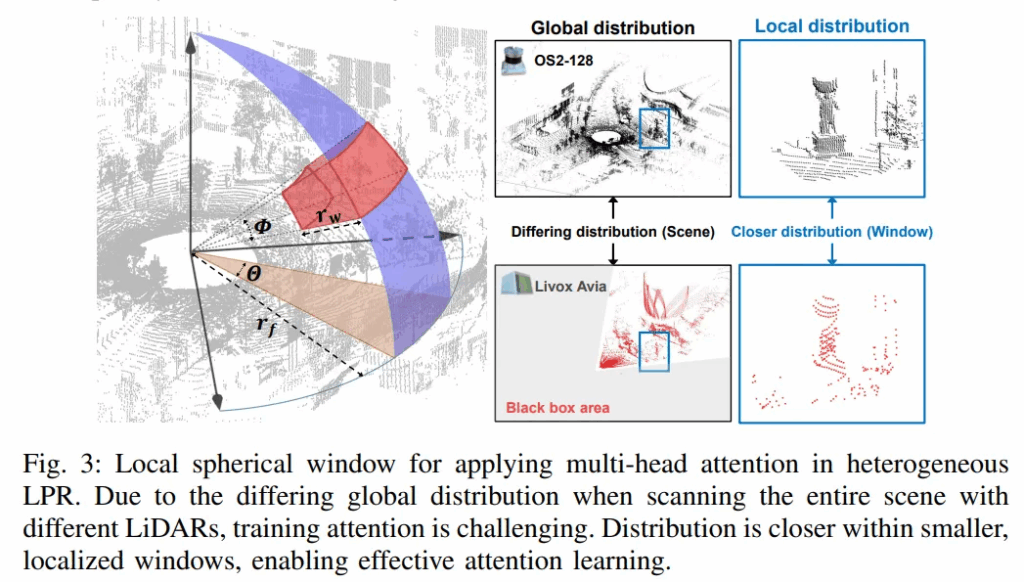
2.3. Feature Aggregation with optimal transport
서로 다른 LiDAR 는 당연하게도 최종적으로 추출되는 local features의 개수도 다릅니다. 이를 효과적으로 하나의 global descriptor 로 합치기 위해 HeLiOS는 clustering 기반의 접근법을 사용합니다. 특별할 건 없고 vision 분야에서 제안된 SALAD 라고 하는 feature aggregation 기법을 LiDAR 환경에 맞게 조금 바꿔서 사용하게 됩니다.
먼저, 각 local features가 m개의 클러스터 중 어디에 속할지를 예측하는 score matrix S 를 계산합니다. 이때 정보 가치가 적은 feature를 걸러내기 위해 dustbin(쓰레기통) channel 을 추가합니다. 이후 최적 수송 이론(optimal transport)에 기반한 Sinkhorn 알고리즘을 사용하여 feature들을 가장 적합한 cluster에 할당하고, 이를 통해 최종적으로 집계된 feature matrix V를 계산합니다. clustering 과정에서 잃어버릴 수 있는 global 정보를 보완하기 위해, GeM pooling과 MLP를 통해 얻은 global representation G를 함께 사용합니다. 최종 global descriptor는 이 둘을 합쳐서 생성됩니다. (g = V+G)
2.4. Overlap Guided Metric Learning
앞서 한번 언급드렸다시피 이전의 LPR 방법론들은 positive, negative 쌍을 구성할 때 거리 (meter) 기반으로 샘플링을 진행합니다. 하지만 이종 LiDAR 환경에 이를 동일하게 적용하게 되면 학습 쌍이 잘못 구성될 수 있습니다. HeLiOS 에서는 이를 해결하고자 두 point clouds 의 overlap 을 직접 계산하여 이를 학습에 활용하게 됩니다.
<Overlap-Based Data Mining>
두 point clouds P_1, P_2 이 있다고 할 때, 이 둘간의 overlap 은 한 point cloud 의 각 point 에서 다른 point cloud 까지의 Nearest Neighbor 거리를 계산하여, 특정 threshold (\tau) 보다 가까운 point 들의 비율로 정의됩니다. 아래 수식처럼 말이죠.
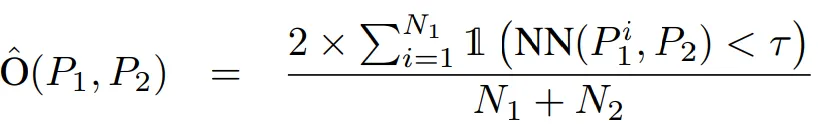
해당 방식은 point clouds를 2D image 로 변환할 필요 없이 3D 공간에서 직접 overlap을 계산하기 때문에 이종 LiDAR 환경에 매우 강건하다고 저자들은 설명합니다. 그리고 이렇게 계산된 overlap 값에 따라 데이터 pair 를 positive (overlap>0.5), semi-positive (0<overlap<0.5), negative(overlap=0) 으로 나눠서 학습에 사용한다고 합니다.
Overlap 계산에 대한 그림은 아래와 같습니다.
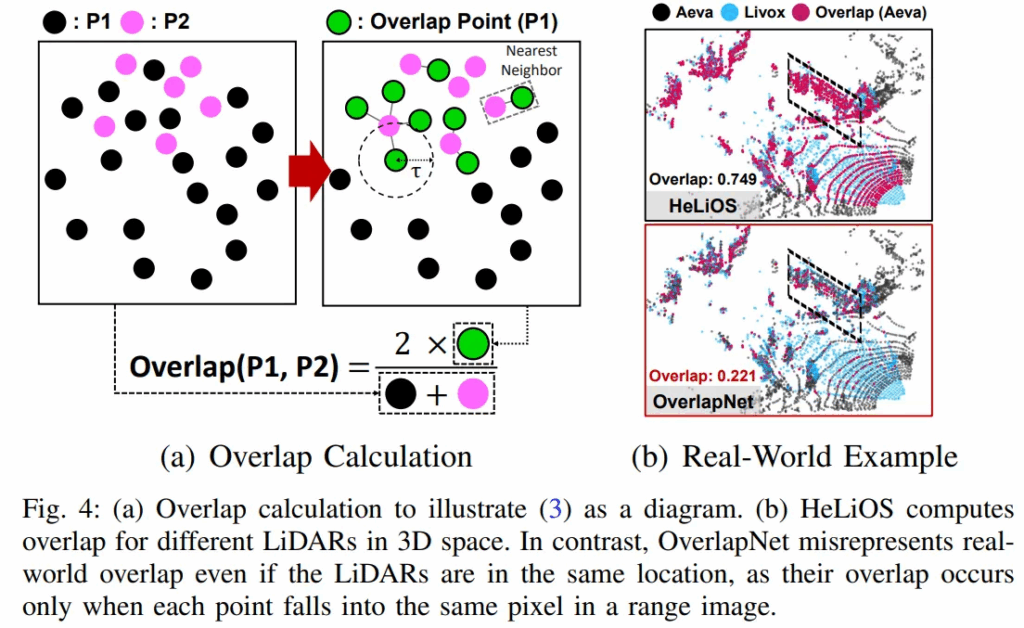
<Guided-Triplet Loss>
저자들은 loss 계산때도 앞서 계산된 overlap 값을 반영하고자 하였습니다. overlap 값에 따라 triplet loss의 margin 이 조절되는 Guided-Triplet Loss 를 설계합니다. 조절되게되는 margin \alpha_{uv} 는 아래와 같습니다.
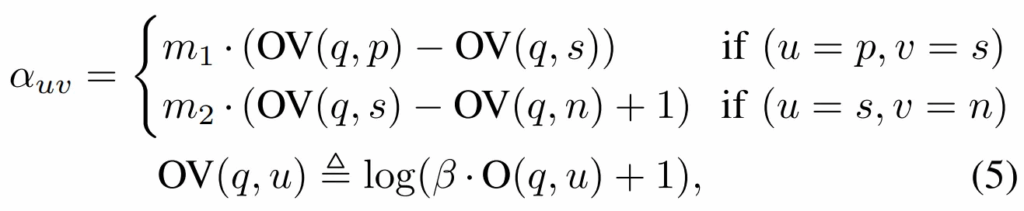
그리고 이를 사용한 loss 식은 아래와 같습니다. embedding space 에서 각 descritpors 들이 더 정교하게 구분성을 가지면서 분포되도록 학습이 진행된다고 합니다
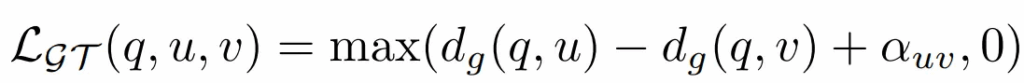
최종 loss term 은 아래와 같습니다. 이전 논문들에서 사용되는 L_{TSAP} 에다가 저자들이 제안한 L_{GT} 2가지를 더해서 사용하게 됩니다. 2가지인 이유는 pos-semi pos 간 한번, semi pos-neg 간 한번 이렇게 총 두번 계산되기 때문입니다.
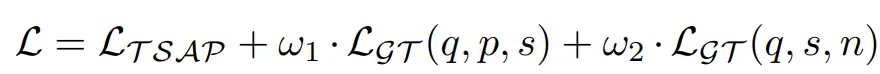
3. Experiment
3.1. Heterogeneous LiDAR Place Recognition
본 실험은 HeLiOS의 핵심 성능을 검증하기 위해 4가지 다른 종류의 LiDAR (Ouster, Livox, Aeva, Velodyne)를 포함하는 HeLiPR 데이터셋을 사용했다고 합니다. 이도 마찬가지로 김아영교수님 연구실에서 취득한 데이터셋입니다.
실험을 위해 Aeva, Livox와 같이 FoV가 좁은 LiDAR 그룹(“Narrow“)과 Ouster, Velodyne처럼 FoV가 넓은 그룹(“Wide“)을 나누어 평가를 진행합니다. 예를 들어, Ouster 센서 데이터를 데이터베이스로 구축하고, 나머지 4종류의 센서 데이터를 쿼리로 사용하는 식으로 LiDAR place recognition 실험을 진행합니다. 우선 결과는 아래 표와 같습니다.
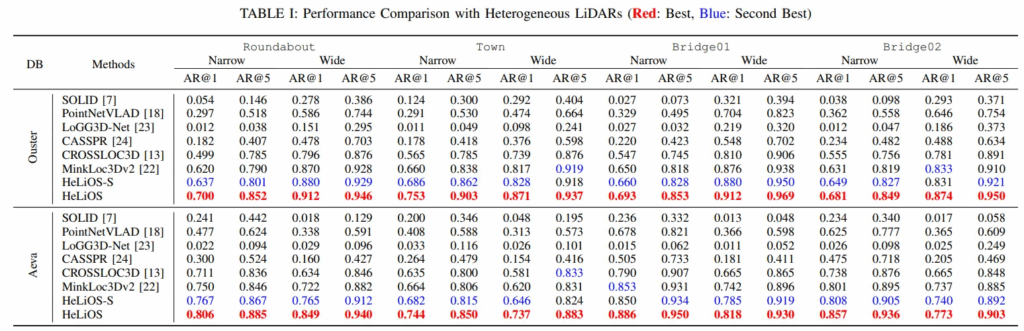
위 표에서는 여러 장소(Roundabout, Town, Bridge)에서의 실험 결과를 보이고 있습니다. HeLiOS와 경량화 버전인 HeLiOS-S는 모든 테스트 시나리오에서 다른 SOTA 모델들을 큰 차이로 능가하는 모습을 보이고 있습니다. 여기서 HeLiOS-S 는 기존 HeLiOS 보다 global descriptor dimension이 조금 작은 버전이라고 생각하시면 됩니다.
3.2. Long-term Place Recognition with Heterogeneous LiDAR
또한 시간적 변화에도 과연 HeLiOS 가 강인한지를 평가하기 위해 Long-term 환경에서의 실험도 진행했습니다. 2023년에 HeLiPR 데이터셋의 Ouster(OS2-128) 센서로 구축된 것을 DB로, 그리고 4년전인 2019년에 MulRan 데이터셋의 이종 LiDAR 센서(OS1-64)로 취득한 것을 Query 로 사용하여 실험을 진행했다고 합니다. 결과는 아래와 같습니다.
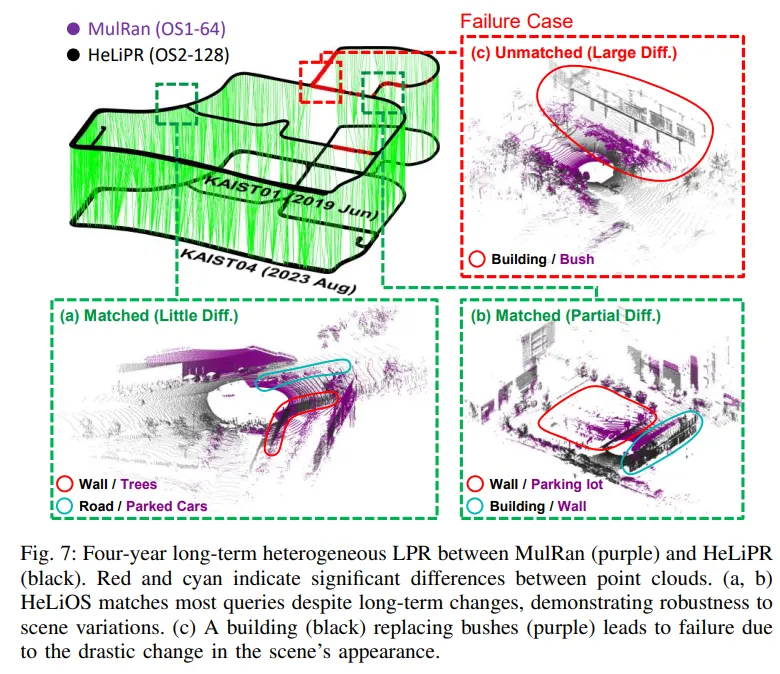
(a), (b)에서 볼 수 있듯이, 4년의 시간동안 나무, 건물 등 여러 환경이 바뀌었음에도 불구하고 HeLiOS 는 대부분의 장소를 성공적으로 매칭하고 있습니다. 이를 통해 저자는 이종 센서간 매칭 뿐만 아니라 long-term 한 상황도 잘 해결할 수 있다고 주장합니다. 그리고 (c) 는 매칭이 실패한 경우인데, 과거엔 수풀이였던 영역에 건물이 들어선 경우라고 합니다. 이에 대해선 오히려 HeLiOS 모델이 두 장소가 (2023 vs 2019년) 다르다는 것을 정확히 인지했기 때문에 분별력이 높은것을 증명하는 결과라고 저자들은 주장합니다.
3.3. Ablation
다음은 최종 descriptor 의 dimension 이 변함에 따라 측정되는 성능과 runtime(ms) 의 변화 테이블 입니다. 우선 결과는 아래와 같습니다.
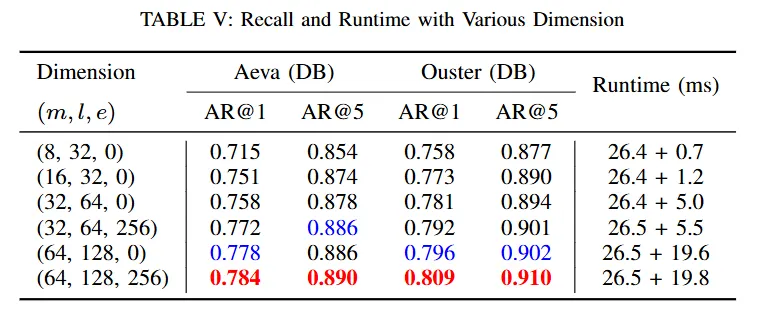
descriptor 의 dimension은 위에서 ml+e 로 계산된다고 보시면 됩니다. 가령 표 제일 아래 모델의 경우 64 *128+256 = 8448 채널의 descriptor 인것입니다. 그리고 runtime 의 경우 모델 inference time 과 retrieval time 을 ‘+’를 기준으로 분리하여 표기하였습니다.
결과적으로 당연히 dimension 이 클수록 모델 성능은 높아집니다. 하지만 이에 따라 retrieval time 이 꽤나 증가하기 때문에 사용하는 환경에 따라 유동적으로 선택할 수 있다고 합니다.
네, 오랜만에 리뷰를 작성해서 좀 어색하긴 하네요. 읽을때와 리뷰할때 모두, 문제정의와 이에 대한 방법론 설계까지 매우 잘 구성된 논문이라는 생각이 계속해서 드는 것 같습니다. 역시 김아영 교수님 연구실이네요.
이상으로 리뷰 마치겠습니다. 감사합니다.
