[CVPR2023]Causalainer: Causal Explainer for Automatic Video Summarization

비디오 요약은 입력된 비디오에서 중요하다고 여겨지는 프레임을 선택하거나 중요도 순으로 점수를 매기는 과제입니다. 그러나 모델이 데이터에 대해 중요도하다고 평가하는 이유에 대해 분석할 방법이 없다는 것이 해당 태스크의 문제 중 하나로 남아있는데요, 본 논문은 이러한 태스크의 내제적 모호성을 해결하기 위한 방법을 소개합니다. 대표성, 흥미도와 같은 중요도에 영향을 미치는 요인을 직접적인 변수로 예측하여 해당 데이터가 높은/낮은 중요도로 평가되는 이유를 명확히 하는 방법을 사용하는데요, 해당 변수를 도입하여 프레임의 노이즈, 화질등의 요소가 아닌 맥락적 중요성이 평가에 핵심이 되도록 했습니다. 자세한 방법은 리뷰를 통해 알아보겠습니다.

---

Motivation: 왜 인과관계에 대해 설명가능해야 하는가?

위의 Figure1은 사람이 요약한 비디오(위)와 당대 SOTA인 video summarization 방법론으로 요약된 비디오(아래)를 시각화 한 것이며, 캡션에서 확인할 수 있듯이 붉은 색이 제외된 프레임이다. 사람이 요약한 비디오의 경우 중요한 클립에 대해 연속성등을 고려해 중간에 한두 프레임이 제거되지 않았다. 반면 ML기반의 요약 결과는 중간에 한두 프레임이 제거됨을 확인할 수 있다. 또한 요약된 비디오 프레임의 예시를 보면 위의 경우 흥미와 내용적으로 중요한 프레임을 선별했음을 알 수 있다. 그러나 아래의 예시의 경우 역동적이거나 움직임이 많아보이는 즉, 시각적 단서(visual cues)에 집중해 비디오 요약을 수행했음을 예측할 수 있다.

이처럼 사람이 비디오 요약을 수행할 때는 흥미로움, 대표성, 스토리의 연속성과 같은 다양한 요소를 고려한다. 그러나 기존의 방법론의 경우는 위처럼 생성된 데이터셋을 기반으로 흥미로움, 대표성과 같은 내제적 고려요인을 모델링하지 않은채로 시각적 단서에 의존해서 요약을 수행했다.

즉, 본 논문은 흥미도, 대표성과 같은 비가시적 요인의 예측에 미치는 영향(인과관계)를 명확히하여 기존 방법론이 예측에 시각적 단서만을 고려하는 한계를 해결하고자 했다. 아쉽게도 이에 대한 정성적 실험은 없지만, SOTA를 달성하는 등 정량적 수치로 제안 방법의 효과를 증명하였다.

Methods

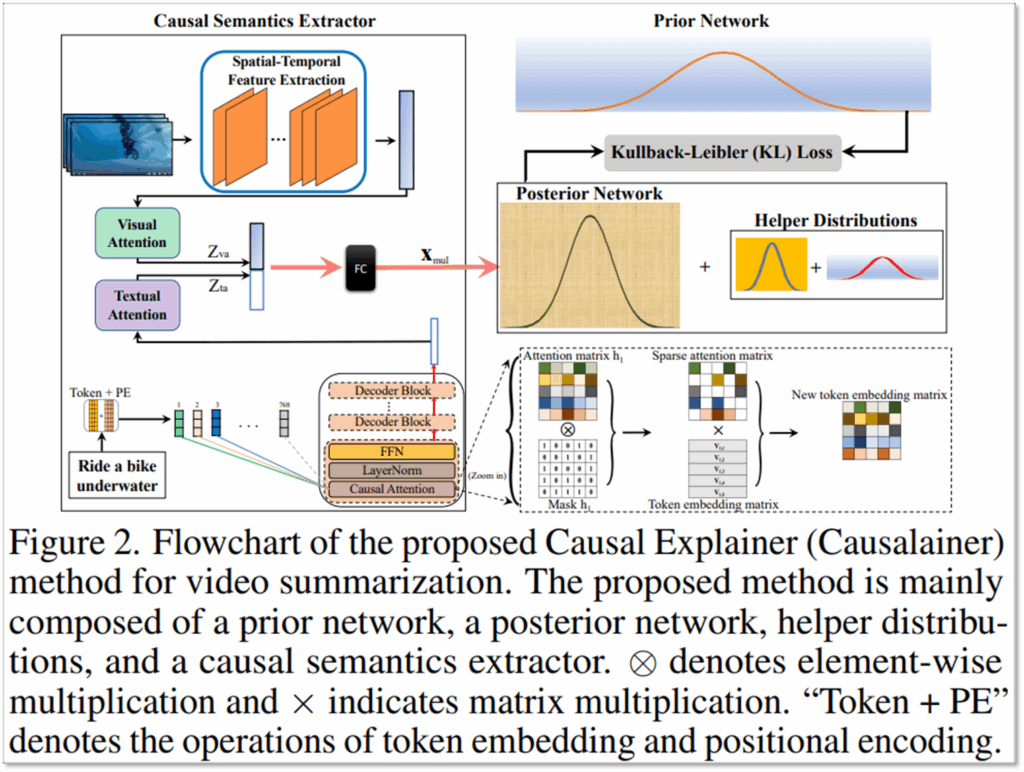
본 논문은 설명가능한 비디오 요약장치인 Causal Explainer(Causalainer)를 제안하였다. 위의 Figure2는 제안한 방법의 Flowchart이다. 좌측의 Causal Sementic Extractor가 제안한 모델에 해당한다. 프레임단위(1FPS) 나뉜 이미지와 같이 입력된 텍스트를 통해 임베딩된 feature X_mul을 생성한다. 이후 X_mul을 통해 y, t, Z 값을 예측한다. 이때 y가 데이터에 대한 최종 모델의 예측 score이다.

설명에 앞서 Causalainer가 도입한 네가지 파라미터(y, t, X, Z)에 대해 소개하면 다음과 같다(Figure3 참조). 먼저 y는 모델의 최종 예측으로 일반적인 비디오 요약 방법론의 예측 결과에 해당한다. t는 e데이터 개입(data intervention)로 입력 데이터에서 발생하는 누락, 블러, 노이즈를 모델링하기 위한 변수이다. 다음으로 X는 입력 비디오에 해당한다. 마지막으로 Z가 본 논문의 핵심 파라미터로 잠재 혼란변수(unobserved confounders)를 의미하며 관측된 데이터(X) 외에도 예측 결과(y)에 영향을 미치는 주관적 잠재요인들(흥미도, 대표성)을 의미한다. 본 논문은 각 파라미터를 분포로 모델링하여 학습하였다. 특히 사전확률을 정의하고 학습데이터를 통해 더욱 적합한 분포(사후확률)로 근사하도록 학습(베이지안 러닝)하였다.

사전 분포의 정의

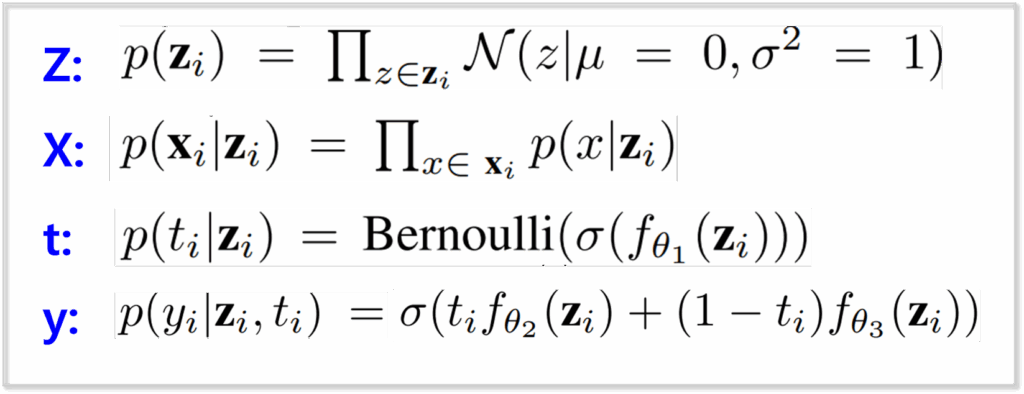
사전 분포는 변수별로 위와 같이 정의되었다. Z는 연속성 있는 정규분포로, t는 이산 데이터이므로(노이즈 있음/없음) 베르누이 분포로 모델링되었다. 내제 데이터인 z가 입력데이터x 생성에 관여함을 가정하며, 최종 예측의 경우 z와 t을 기반으로 생성된다.

사후 분포의 정의

x는 관측 데이터이므로 우리는 관측(x, y)을 통해 z와 t의 분포를 업데이트하도록 marginalize해서 모델링해야하며, 그 방법은 아래와 같다. 아래의 수식을 통해 관측 x, y를 활용하여 z를 모델링 할 수 있음을 알 수 있다.

목적함수

일반적으로 베이지안 러닝의 경우 사전확률과 사후확률이 같아지도록 하는 ELBO를 목적함수로 하여 학습한다. 해당 논문 또한 ELBO 역할을 하는 term과 helper loss라는 term을 통해 목적함수를 설계하였다. helper loss는 ϕ_k(k=5,6,7)를 도입해 t를 모델링하기 위한 보조 term이다. 위의 사후분포에서 관측값을 통해 z를 위주로 모델링하였기에 helper term으로 주된 t 생성 분포를 학습하는 것이다.

그 외

본 논문은 위의 설계 외에도, 멀티모달 입력에서 텍스트의 입력이 종종 전반적인 성능에 악영향을 미치는 현상을 해결하고자 일부 테크닉을 적용했다. 다만 텍스트 입력의 악영향에 초점을 맞춘것으로 보아 멀티모달을 위한 설계라기 보다는 시각 정보 입력에 중점을 둔 비디오 요약 수행을 위한 설계라고 보는게 좋다.

논문이 제시한 방법은 텍스트 입력에만 causal attention 구조를 두어 입력된 텍스트 데이터에세 유용한 정보만을 연산에 활용하도록 하는 것이다. 해당 연산 구조를 확대해서 보면 아래와 같다.

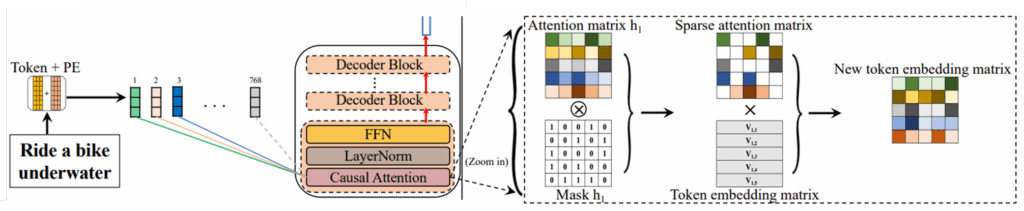
기존 Transformer 기반의 방법의 경우 Positional Encoding(PE)가 결합된 토큰들을 Self-attention 연산을 수행했다. 그러나 causal attention에서는 attention matrix에서 top-k개만(그림의 Mask h)을 key에 attention 하도록 설계했다.

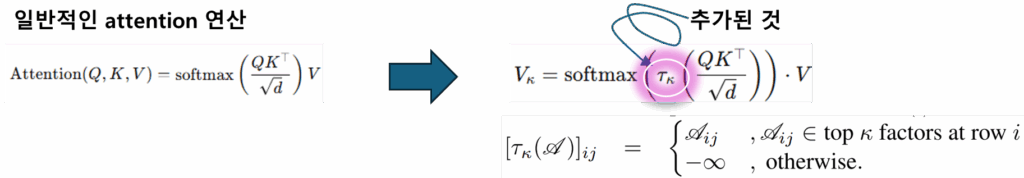
실험 결과

실험은 아쉽게도 분석 실험보다는 SOTA와의 정량적 성능 비교 위주로 진행되었다. 대신 다양한 세팅에서 실험을 진행하였는데, Fully supervised (1FPS 기준, 1초단위로 중요도 라벨 존재), Multi-modal supervised (텍스트 쿼리와 영상을 동시에 입력), Weakly-supervised(1FPS 기준, 2초단위로 중요도 라벨 존재, 기존 방법론의 평가방식에 따른 정의라고 함) 세팅에서 실험결과를 보였다. 실험은 대표적인 비디오 요약 데이터셋인 TVSum, QueryVS, SumMe에 대해 진행되었으며, 평가 방식은 F1-score로 리포팅 되었다. 이는 ground-truth와 모델이 예측한 중요 프레임의 겹치는 정도를 의미하여 높을수록 좋은 평가방식이다.

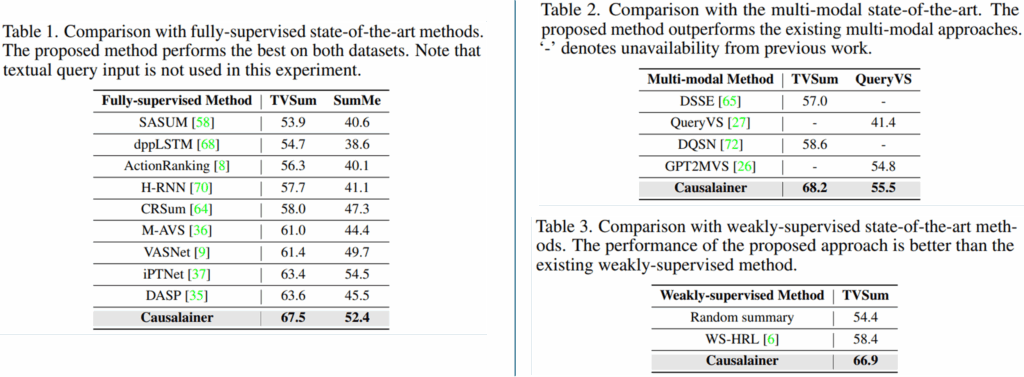
위의 실험 결과 모든 세팅에서 비교 SOTA 방법론 대비 높은 성능을 거두었음을 확인할 수 있다. 본 논문에는 별도의 추가 분석 실험은 없었지만, 해당 성능 향상의 원인을 인과 추론 능력 강화 때문이라고 밝혔다. 실험이 이렇게 간단한 이유는 제안한 프레임워크 자체의 이점 때문이다. 프레임워크는 인과관계에 대한 파라미터 도입으로 예측의 설명가능성을 높였는데, 이는 비디오 요약이 잘못될 수 있는 상황, 예를 들어 관제 비디오를 요약했는데 강도가 들어온 프레임을 누락했다,의 예방효과를 기대할 수 있다고 한다(Figure.4 참조). 그러나 이러한 부수적 효과를 증명하려면 정성적 결과가 필요할 것 같은데, 이에대한 결과가 없어 아쉽다.

논문 초반에 data intervention의 도입은 일반적으로 causal relation을 개선한다는 언급(Figure. 5 참조)이 있었는데, 이러한 인사이트를 video summerization에 확장가능함을 보인것에 가치가 있는 논문으로 생각된다. (레퍼런스된 논문은 모두 video summerization 연구가 아님) 다만 내제적 변수인 z가 아닌 t의 도입이 성능 개선에 큰 영향을 미쳤을 것 같다는 찝찝함이 있는데 이에 대한 분석이 없는 점이 아쉽다.