안녕하세요 3번째로 리뷰할 논문은 2025년에 AAAI에 기재된 Zero-shot depth completion via Test-time Alignment with Affine-invariant Depth Prior라는 논문입니다.
논문 : https://arxiv.org/abs/2502.06338

제목에서 알 수 있듯이 Depth Completion 문제를 다루며 특히 Zero-shot 환경에서의 일반화 성능에 집중합니다. 사전학습된 Monocular depth prior 를 활용하여 sparse depth 를 dense depth 예측을 학습없이 수행하는 최초의 논문입니다.

Diffusion을 활용한 depth completion task를 처음 접하다 보니 논문을 이해하는 데 많은 시간이 걸렸고,
아직 부족한 부분도 많지만 최대한 상세히 리뷰를 해보도록 하겠습니다!

Abstract & Introduction

Depth completion을 이해하기 위해서는 우선 Depth map 의 형태에 대해서 아는 것이 필요합니다. 일반적으로 Depth map의 결과는 다음 두 가지 형태로 나누어집니다

• Metric depth: 실제 거리를 나타내는 값입니다. 예를 들어 LiDAR 센서로부터 얻어진 depth입니다. Metric depth는 실제 거리 정보를 담고 있기 때문에 3D reconstruction, obstacle avoidance와 같은 작업에 직접적으로 활용될 수 있습니다.
• Relative depth: 실제 거리 값이 아닌, 이미지 내에서 상대적인 거리 관계만을 나타내는 값입니다. 예를 들어 어떤 픽셀이 다른 픽셀보다 멀리 있는지 또는 가까이 있는지만 알 수 있습니다. 즉, 실제 거리(scale)는 모르는 상태입니다.

실제 응용 분야에서는 metric depth를 정확하게 예측하는 것이 중요하지만, 이를 바로 얻기가 쉽지 않습니다.
센서마다 각기 다른 한계점을 갖고 있기 때문입니다. 예를 들어 LiDAR는 정확한 metric depth를 제공하지만 데이터가 sparse하여 dense depth를 얻기 어렵고, 카메라 기반의 monocular depth estimation은 dense하지만 relative depth만을 제공합니다.

또한 실제 환경에서는 센서 노이즈와 outlier 문제가 빈번하게 발생하여 sparse depth 데이터의 신뢰성을 크게 저하시킵니다. 게다가 기존 학습 기반 모델은 특정 데이터셋에서만 우수한 성능을 보이고, 새로운 환경에서는 성능이 떨어지는 domain gap 문제가 존재합니다.

이러한 배경을 가지고 있음에도 불구하고 본 논문은 monocular depth estimation을 zero-shot 환경, 즉 별도의 학습 과정 없이 unseen 데이터에서도 우수한 성능을 보이는 방법을 제안합니다.

이를 가능하게 한 핵심은 바로 Foundation model의 활용입니다. 대규모 데이터셋을 통해 사전학습(pre-training)된 모델이 다양한 downstream task에서 강력한 일반화 성능을 보이는 것으로 알려져 있습니다. 이 논문 역시 이러한 Foundation model의 아이디어를 Depth completion에 최초로 도입합니다.

사전학습된 (RGB-D 기반) Affine-invariant Monocular Depth Prior를 기반으로 Metric depth사이의 alignment를 맞추어 zero-shot으로의 Depth completion을 수행하였습니다
(여기서Affine-invariant depth는 이미지 내에서 상대적인 깊이 관계를 표현하는 depth입니다. 하지만 일반적인 relative depth와 달리, 이름 그대로 affine 변환에 대해서는 불변성을 유지합니다. metric scale은 알 수 없지만, 이미지 내 상대적인 깊이 차이는 일정한 affine 변환 내에서는 변하지 않고 유지됩니다)

input이 RGB인데 inference 만으로 어떻게 sparse한 depth를 dense metric으로 변환하지라는 의문이 들수 있습니다. 추론 과정에서 sparse depth를 직접 input으로 넣는 것이 아니라, 신뢰성있는 sampling된 depth 예측 결과와 sparse depth 사이의 차이를 guidance로 활용하는 최적화 방식을 사용합니다.
이 구체적인 방식은 method 파트에서 다시 자세히 설명드리겠습니다.

본 논문의 주요 아이디어는 다음과 같습니다.

• 먼저, Diffusion 모델 기반의 foundation model을 사용하여 일반화 능력을 향상시키는 depth completion 제안
• 하지만 Affine-invariant depth는 metric depth를 직접 제공하지 않기 때문에 실제 거리로 변환하는 과정에서 Test-time alignment를 통해 최적화하여 relative depth를 metric depth로 변환
• outlier filtering 기법을 제안하여 sparse depth에 존재하는 노이즈와 outlier를 효과적으로 제거함으로써 depth alignment의 신뢰성을 향상

Method

Preliminary

Diffusion 모델은 원본 데이터에 time-step 별로 노이즈를 추가한 뒤 reverse(noise 제거) 과정으로 원본 데이터로 복원하는 과정을 통해 데이터의 분포 p(x)를 모델링합니다. 이 논문에서 사용된 diffusion 모델은 데이터 분포의 log-density를 직접적으로 모델링하는 Score-based Diffusion입니다. 이는 밑에 식으로 표현됩니다

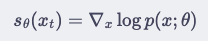
여기서 $s_{\theta}(x_t)$는 주어진 time-step에서 데이터가 어떤 방향으로 움직여야 원본 이미지에 가까워지는지를 나타내는 gradient, 즉 score를 의미합니다.

이러한 score를 활용하면 기존의 diffusion 모델처럼 단순히 무작위 이미지를 생성하는 방식이 아닌 저희가 원하는 형태의 이미지를 생성하는 Guided Diffusion이 가능합니다.
Guided Diffusion에서는 이 score를 통해 원하는 이미지로 생성을 할 수있게 만들어주는 핵심적인 역활을 수행하는 것이 guided diffusion에 핵심입니다.

그렇다면 저희는 sparse depth 와 일치하는 depth를 생성할 수 있을 것입니다

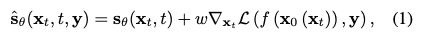
• w : 가이드의 정도를 조절하는 가중치
• y : 조건 (원하는 이미지 스타일, 여기서는 sparse depth y)
• f(x0​(xt​)) : x0(xt))를 변환하여 제공하는 조건과 비교할 수 있도록 하는 함수
• L(f(x0(xt)),y) : 조건 y와 비교하는 loss

즉, 쉽게 말로 풀어서 설명드리면 Xt에서 노이즈가 섞인 상태와 X0의 복원하고자하는 이미지와 사후 확률을 기반으로 gradient 방향을 구하여 sparse depth y와 일치하도록 보정해주는 것 입니다.

이로써 uncoditinonal 한 모델이 conditional model로 확장되었다로 이해해주시면 될 것 같습니다.

Inverse problem

그렇다면 여기서 한 가지 의문이 생깁니다.
“Unconditional 모델을 조건부 모델로 확장한다고 해서, 정말 우리가 원하는 dense depth를 정확히 생성할 수 있을까?” 단순히 sparse depth를 조건으로 걸었다고 해서 모델이 그 정보를 반영할 수 있으리라는 보장은 없습니다. 특히나 sparse depth는 정보량이 매우 제한적이기 때문에, 모델이 복원 과정에서 구조적 일관성을 유지하면서도 sparse depth를 dense depth를 생성하기란 쉽지 않습니다.

이러한 문제를 해결하기 위해, 저자는 이를 inverse problem의 관점에서 접근합니다. 즉, sparse depth(y)를 관측값으로 보고, 이로부터 원래의 dense depth (x)를 추론하는 문제로 재정의하는 것입니다. 이는 본질적으로 ill-posed 문제(하다마드 조건)이기 때문에 추가적인 prior가 필요합니다.

따라서 저자는 이 문제를 최적화 문제로 재정의하게됩니다.

1. 즉 예측된 dense depth x는 sparse depth (y) 와의 likelihood p(y|x)
2. 일반적인 depth 분포를 따르는 prior p(x)

이를 수식으로 표현하게 베이즈 정리를 이용하여 아래와 같이 Maximum a Posterior(MAP)를 추정하여 해결 할 수 있습니다

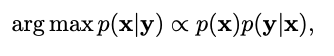
자 그렇다면 여기서 P(x), P(y|x)에 log를 씌움으로써 minimization으로 바꿀 수 있습니다.

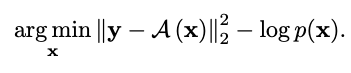
A(x) => x에대해 forward 적용 결과입니다. 이렇게되면 sparse한 부분과 일반적인 depth 분포를 따르는 두 정보를 최적화 할 수 있게 됨으로써 최적화가 가능해집니다.
그렇다면 이 부분을 guided score smapling 에 적용을 해야합니다 정확한 prior를 따르면서도 sparse depth 조건을 만족하는 방향으로 복원 과정을 조정해야합니다

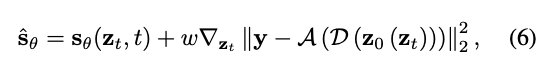
각 항에 대한 해석은 앞서 설명한 것과 동일하며, 다만 입력 공간 x에서 latent 공간 z로 표현이 바뀐 것이 주요 차이점입니다. 이는 Latent Diffusion 구조를 적용했기 때문입니다. 원래의 image space x에서 수행되던 guided sampling을 latent representation z 상에서 수행하도록 확장한 것입니다. 이때 decoder D는 latent z를 다시 depth map x로 복원해주는 역할을 수행하며, forward operator A는 복원된 depth map에서 sparse 위치에 해당하는 값들만 추출하여 조건 y (sparse depth)와 비교하게 됩니다.

Test-time Alignment with Hard Constraints

다음으로는 이 논문에서 제안한 핵심적인 부분이라고 생각하시면 될 것 같습니다. TTA 방식은 diffusion 과정 중간에 최적화 루프를 삽입하여 sparse depth를 hard constraint로 활용하는 방식입니다. 이 방법은 Test 시점에서 수행되며 학습없이도 sparse depth와 일치하는 결과를 생성할 수 있게 해주는 부분이라 핵심입니다.

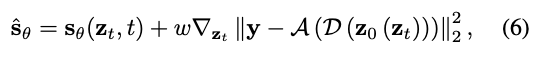
위 식은 확률적으로 sampling을 유도하는데 사용이 된다고 말씀을 드렸습니다. 하지만 diffusion 모델 특성상 sampling은 확률적으로 이루어지기 때문에 같은 입력 Z에 대해서도 매번 생성되는 결과는 달라질 수 밖에 없습니다. 단순히 위 식을 기반으로 score 방향을 보정해주는 것 만으로는 정확히 일치하는 결과를 보장할 수는 없다는 것입니다. 이러한 한계를 보완 하기 위해서 저자는 inference 과정에서 optimization loop를 추가해 줍니다. Z0(Zt) 식을 계속해서 조정해주는 것입니다. 이를 저자는 hard constraint로 작동하게하며 sampling이 진행되는 도중에도 지속적으로 align을 맞춰주는 방식입니다.

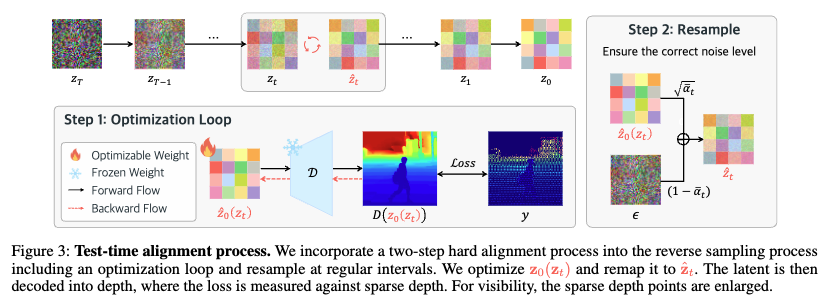
위 fig는 제자가 제안한 TTA 방법론이며 총 두가지의 step으로 나뉘게 되는데요

Step 1의 Optimization Loop는 현재 시점의 latent 벡터 z_t를 입력으로 받아, decoder D를 통해 복원된 depth 맵 D(z_0(z_t))를 얻고, 이를 ground truth sparse depth y와 비교하여 loss를 계산합니다. 이 loss에 대한 gradient를 이용해 z_t 자체를 반복적으로 업데이트합니다.

복원될 dense depth 맵 D(z_0(z_t))는 아직 noise가 제거되지 않은 중간 latent representation인 z_t입니다. 이 단계에서의 최적화 alignment step으로 작동합니다. 이때 핵심은 projection 연산 A(·)입니다. 이 연산은 복원된 dense depth 중 실제 sparse depth y가 존재하는 위치만을 추출하여 비교함으로써, 모델이 sparse한 정답 위치에 더욱 정확히 맞추도록 유도하는 역할을 합니다.

Step 2는 Step 1에서 최적화된 결과를 기반으로 다시 diffusion 경로에 올바르게 resampling시키는 과정입니다. 앞서 Step 1에서는 중간 latent representation인 z_t에서 시작해 복원된 z_0(z_t)가 sparse depth y와 일치하도록 최적화하였습니다. 그러나 이 과정은 기존 diffusion 고유의 노이즈 스케줄을 왜곡할 수 있다고 합니다. 따라서 Step 2에서는 noise resampling을 수행하여, 현재 time-step t에 맞는 올바른 분포를 다시 부여합니다. 아래와 같은 수식을 따릅니다.

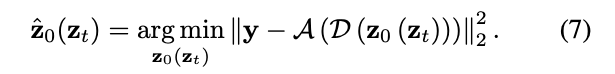
alignment 맞추것에 다시 resampling을 해줌으로 써 diffusion 모델의 시간적 노이즈 스케줄에 맞춰주는 것이 핵심입니다
(노이즈 스케줄에 대해서는 diffusion의 개념에 대해서 안다고 생각하고 넘어가도록 하겠습니다.)

그렇다면 기존의 diffusion 과 다르게 sampling -> alignment -> resampling 이 구조라고 보시면됩니다. 이것이 저자가 말하는 hard constraint와 stocaticity를 융합한 구조로 기존의 soft guided sampling과의 차별점이라고 강조합니다.

Affine-invariant depth는 scale과 offset에 영향을 받지 않는 상대적인 깊이 정보를 담고 있습니다. 따라서 이 prior는 metric depth 분포와는 다른 공간에서 작동합니다. 이로 인해 metric depth를 복원하기 위해 affine-invariant prior를 그대로 사용할 수 있을지에 대한 의문이 생깁니다.

왜냐하면 diffusion 모델은 학습 시점에서 affine-invariant depth 데이터의 분포만을 학습하기 때문에,

metric depth와 같은 절대 단위의 데이터를 복원하기 위해선, 해당 데이터가 학습된 분포 내에 존재해야 하기 때문입니다. 하지만 TTA통해 그것을 가능하게했고 실험적으로 증명하였습니다

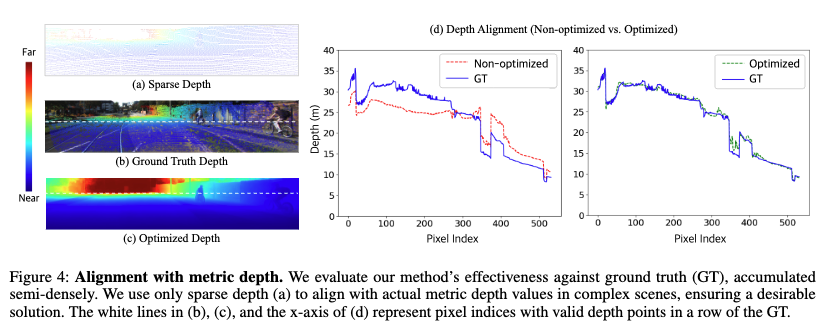
위 실험은 sparse depth만을 활용해 복원된 depth가 실제 metric depth(GT)와 얼마나 alignment되는지를 보여주는 정성적·정량적 비교입니다. (c) Optimized Depth는 alignment 과정을 거쳐 ground truth와 구조적으로 잘 일치하는 것을 시각적으로 확인할 수 있습니다. (d)의 그래프는 optimization 전후의 결과를 정량적으로 비교하며, 최적화를 통해 GT와의 차이가 현저히 줄어든 것을 보여줍니다.

Prior -based Outlier Filtering

실제 센서로부터 얻은 sparse depth는 신뢰하기에는 outlier가 자주 포함됩니다. 이는 depth map 생성에 큰 악영향을 미칠 수 있습니다. 만약, 이러한 포인트들이 alignment 시 supervision 신호로 작동하게 되면, 모델이 잘못된 정답에 맞춰 학습되거나 수렴이 느려지는 문제가 발생할 수 있습니다. 특히 저자의 방법처럼 test-time에 sparse depth를 활용해 optimization을 수행하는 구조에서는, 잘못된 supervision은 직접적으로 복원 품질에 영향을 줍니다.

저자는 이런 문제를 막기 위해 먼저 depth map을 비슷한 깊이를 가진 영역들로 나눕니다. 이때 사용하는 방법이 바로 SuperPixel 알고리즘으로, 비슷한 위치와 깊이를 가진 픽셀들을 하나의 덩어리로 묶는 방식입니다.

이렇게 나눠진 각 영역 안에서는 깊이 값이 거의 비슷하다고 가정할 수 있습니다. 하지만 센서 노이즈나 오류 때문에 일부 포인트는 튀는 값일 수 있어서, 저자는 RANSAC 알고리즘을 적용합니다. 결과적으로 정제된 sparse depth 포인트들만 supervision 신호로 활용하게 되어, alignment 과정의 안정성과 정확성을 높이는 데 핵심적인 역할을 합니다.

Losses

본 논문에서는 세가지 주요 loss function이 존재합니다.
첫번째 loss는 sparse depth consistency loss입니다. sparse depth y 가 존재하는 위치에서 복원된 depth D와의 차이를 최소화 하는 L1 loss 입니다

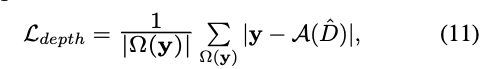
두 번째로는 복원된 Depth map의 gradient가 지나치게 날카롭거나 거칠어지는 것을 방지하게 됩니다. 이는 ‘람다’ 인 항으로부터 RGB 이미지의 texture 경계에 따라 픽셀 간 smoothness를 depth map의 x, y 방향의 gradient에 대해 아래와 같이 L1 loss를 추가하여 과도한 smoothing이 일어나지 않도록 하였습니다.

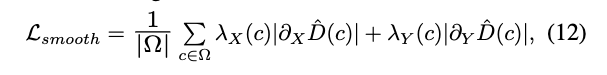
마지막으로는 구조적인 디테일을 보존을 위해서 SSIM으로 부터 밝기 요소를 제거하고 상대적인 구조만을 유지하기 위해서 R-SSIM 구조 유사도 손실을 도입하였습니다.

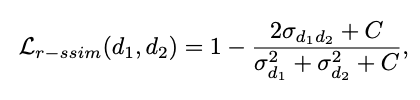
여기서 d1 은 (affine invariant depth) 이고 d2는 metric depth 입니다. 여기서는 두 값이 pixel-wise 하게 정확히 일치할 필요는 없고 구조적으로 비슷한 형태만 유지하면 됩니다. 이미 그에대한 것은 식 (11)에서 이루어졌기 때문입니다.

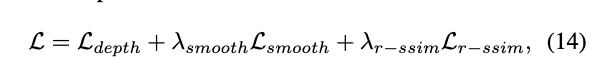
종합된 losss는 위 식과 같습니다.

Experiments

실험에는 indoor 데이터셋,outdoor 데이터셋을 사용하여 평가하였습니다.

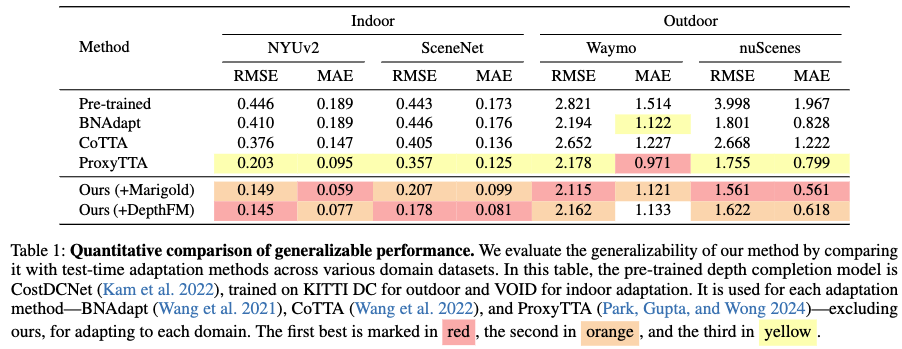
Table 1은 제안한 방법의 domain generalization성능을 기존 TTA기법들과 정량적으로 비교한 것입니다. 평가지표는 RMSE, MAE 입니다. 저자는 Marigold와 DepthFM이라는 diffusion 모델을 사용함으로써 일반화 성능을 갖추었다는 것을 입증하였고 SOTA에 준하는 성능을 달성하였습니다.

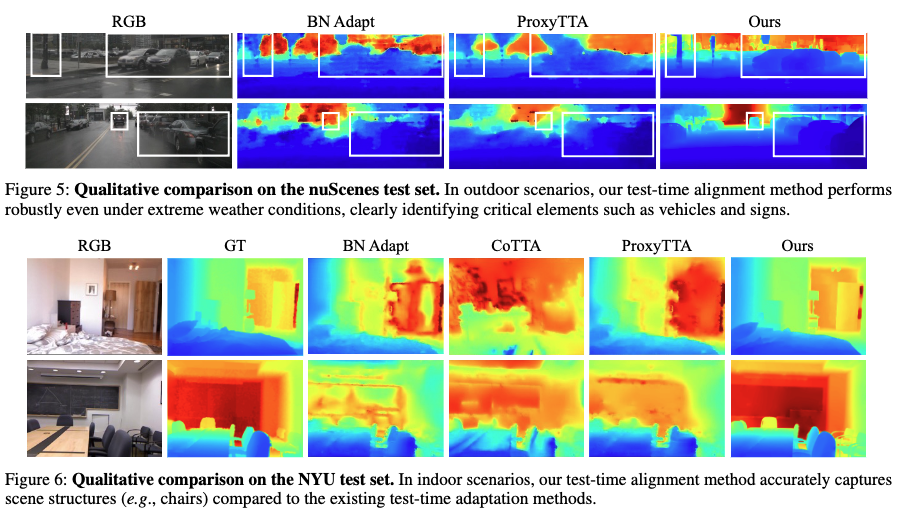
fig 5, 6은 각각 indoor,outdoor 에서의 정성적으로 비교한 그림입니다. 정성적으로 보더라도 기존 deptmap들과의 성능차이를 보실 수 있습니다.
outdoor 는 기존의 raw sparse depth는 그대로 사용할 수 없었다고 합니다. 이는 실제 센서에서 수집된 depth 데이터에 노이즈가 과도하게 포함되어 있어 학습 및 평가에 어려움이 있었기 때문입니다.이를 해결하기 위해 저자들은 기존 raw depth와 RGB 영상을 기반으로 정제된 depth 정보를 생성하는 전처리를 적용했습니다.

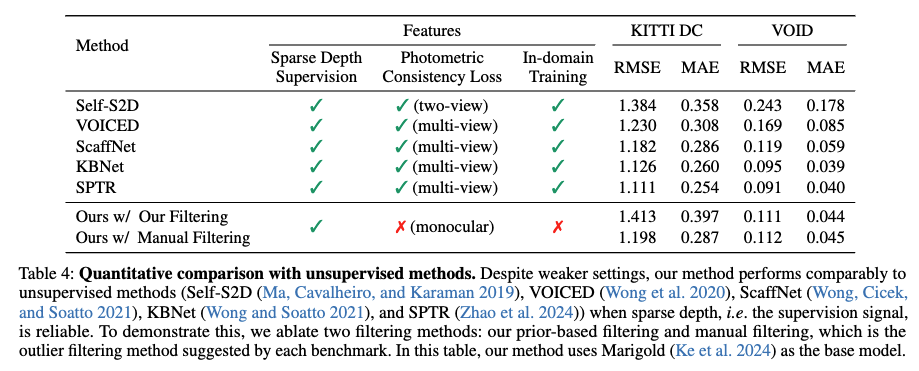
Table 4는 제안한 방법이 unsupervised depth completion 방법들과 비교했을 때도 경쟁력 있는 성능을 보인다는 것을 보여줍니다. 기존 방법들은 대부분 multi-view photometric loss와 in-domain 학습을 활용하지만 제안한 방법은 monocular 입력만으로도 유사하거나 더 낮은 MAE를 달성했습니다.
특히 KITTI DC와 VOID 벤치마크에서 prior-based outlier filtering을 적용한 경우 기존 manual filtering보다 더 일관된 성능을 보였습니다. 이는 제안한 filtering 전략이 신뢰성 있는 sparse depth로 alignment를 유도하는 데 기여했다고 합니다.

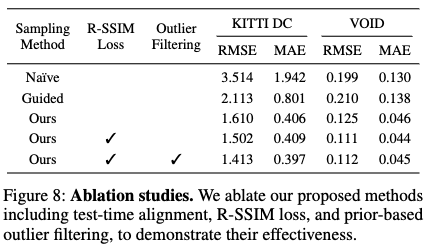
Figure 8은 제안된 TTA기법이 성능에 미치는 영향을 분석한 ablation 실험 결과입니다. Naïve 설정은 alignment 없이 단순 생성만 수행해 성능이 가장 낮았으며, Guided는 alignment를 도입했지만 여전히 불안정했습니다. 이후 점진적으로 R-SSIM을 추가하고 , prior-based outlier filtering까지 적용한 최종 모델이 가장 낮은 RMSE와 MAE를 기록했습니다. 특히 KITTI DC처럼 indoor 보다는 outdoor도메인에서는 filtering 기법의 효과가 더욱 도드라졌다고 합니다. 아무래도 outdoor scene이 indoor 보다 불안정한 outlier들이 많아서 그렇다고 저자는 얘기를 합니다.

결론 : 논문은 monocular 기반 depth prior를 활용한 최초의 zero-shot depth completion 기법을 제안합니다. 제안한 방식은 sparse한 입력과의 alignment를 유지하면서도 다양한 도메인에서 일반화성능을 입증하였습니다.
하지만 diffusion 모델이다 보니 아직까지는 inference에서 속도가 느리다고 합니다. 향후 이런부분을 개선하는 연구를 하겠다고 합니다.