[CVPR 2025] SharpDepth: Sharpening Metric Depth Predictions Using Diffusion Distillation

안녕하세요, 67번째 x-review 입니다. 이번 논문은 CVPR 2025년도에 게재된 diffusion 기반 depth estimation 논문 입니다.

그럼 바로 리뷰 시작하겠습니다 !

1. Introduction

Monocular Depth Estimation(MDE)는 하나의 이미지를 사용하다보니 스케일 모호성과 depth를 예측하기에는 제한된 depth cue만을 가진다는 어려움이 존재하며, 이러한 어려움은 제로샷 세팅에서 더 크게 나타나게 됩니다.

제로샷 MDE는 크게 discriminative와 generative 방식으로 나눌 수 있는데요, 전자는 보통 sparse한 GT depth가 존재하는 데이터셋을 이용한 supervision 방식에 의존한다고 합니다. metric depth값을 직접 예측하도록 하는데, GT 데이터 자체의 sparse함과 depth cue의 부족으로 인해 물체의 경계에서 블러 현상 등이 발생하게 됩니다.

최근에는 후자인 generative 방식이 diffusion 모델을 사용해서 디테일하고 선명한 엣지를 표현하는 depth map을 생성할 수 있다고 합니다. 그러나 latent diffusion 모델의 내재된 한계가 있는데, 바로 완전히 dense한 depth map을 사용할 수 있는 합성 데이터로만 diffusion 기반 depth 모델을 finetuning할 수 있다는 것 입니다. 이로 인해 real 데이터에 적용할 때 도메인 갭이 발생하게 되죠. 또한 이러한 모델은 기본적으로 affine-invariant depth를 예측하는데, 즉 metric depth를 예측하지 않는 것 입니다.

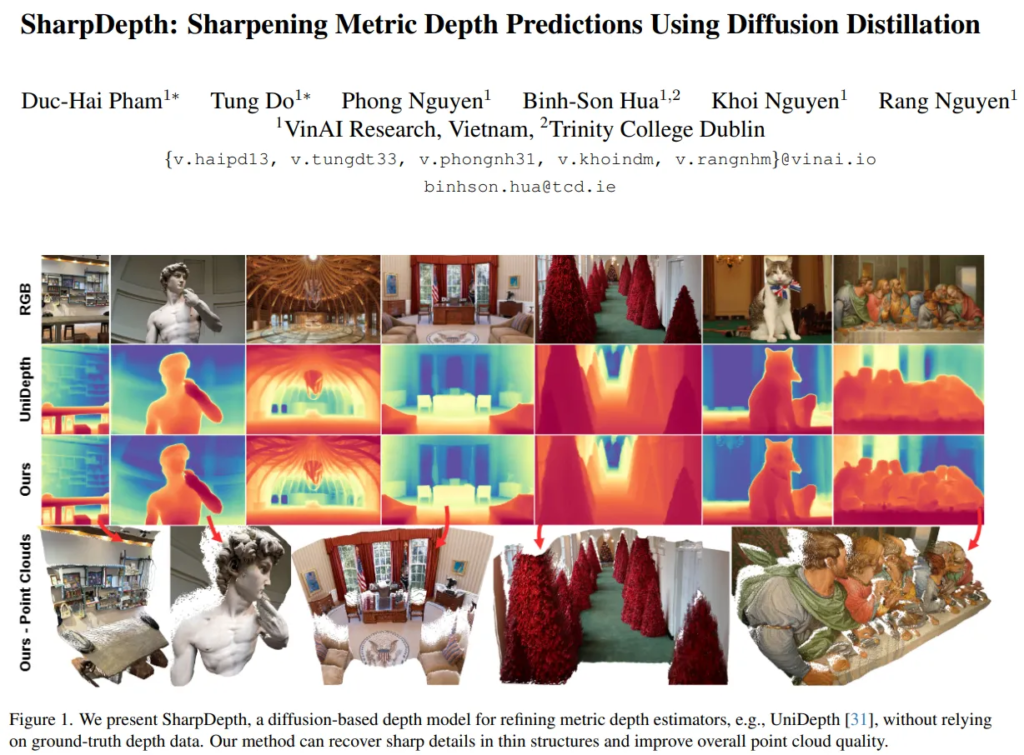
그래서 본 논문에서는 엣지 영역과 같은 고주파의 디테일을 포함한 metric depth를 생성할 수 있도록 diffusion 기반의 모델인 SharpDepth를 설계하고 있습니다. affine-invariant depth estimator를 기반으로 하며, 기존 metric depth 예측 모델의 초기 예측을 개선하여 depth의 디테일을 향상시킨다고 합니다. 이를 위해 affine-invariant 모델과 metric 모델의 depth 예측 결과를 공통된 스케일로 정규화한 다음, 두 예측 사이의 difference map을 생성합니다. 이 difference map을 통해 신뢰할 수 있을만한 이미지 영역과 추가적으로 선명도와 같은 개선이 필요한 영역을 구분할 수 있게 된다고 합니다. difference map에서 불확실한 예측으로 보이는 영역에 diffusion 모델이 좀 더 초점을 맞출 수 있도록 Noise-aware Gating을 제안한다고 합니다.

자세한 방법론에 대해서는 method 파트에서 설명드리며, 본 논문의 main contribution을 정리하면 다음과 같습니다.

1. zero shot 세팅에서 고주파 영역의 엣지 디테일을 가진 metric depth를 생성할 수 있는 diffusion 기반의 SharpDepth 제안
2. 두 개의 noise 인지 모듈을 가지고 real 이미지에 대한 finetuning을 진행하였으며, 이 때 기존의 MDE 방식들보다 약 100~150배 적은 학습 이미지 사용
3. 여러 데이터셋에서 실험 결과, discriminative 방식과 비교할 수 있을 정도의 성능을 가지면서 생성형 모델의 디테일한 출력 결과를 포함

2. Preliminaries

Score Distillation Sampling(SDS)

본 논문에서 사용하는 SDS는 diffusion 모델의 복잡한 역전파 과정 없이도 학습이 가능하도록 하기 위한 distillation 방식이라고 합니다.

기본적인 개념을 살펴보면, x=g(\phi)는 최종 생성된 이미지 x는 어떠한 파라미터 \phi를 가진 함수 g를 통해 생성되는데요, 즉 최적화하려는 대상은 이미지가 아니라 그 이미지를 생성하는 latent 벡터인 \phi라는 것이죠.

다음으로 U-Net에서 자코비언 항을 제거하게 됩니다. 보통 diffusion 모델은 U-Net을 통해 역전파를 하는데, U-Net 안에서 입력에 대해 미분했을 때의 미분 값이 자코비언 행렬이 됩니다. 이는 입력의 변화가 출력에 주는 영향을 나타내는 기울기 정보가 되며, 이 자코비언 행렬을 역전파할 때 계산량이 커지고 복잡해지게 됩니다. 그래서 SDS는 식(3)과 같이 설계되어 U-Net의 자코비언 항을 제거하면서도 학습이 가능하도록 합니다.

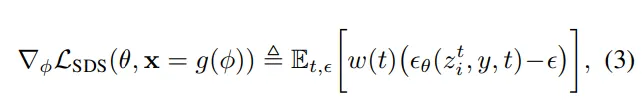
• \epsilon_\theta(z^i_t,y,t) : diffusion 모델이 timestep t에서 노이즈 \epsilon을 예측하는 함수
• w(t) : timestep에 따른 가중치
• y : 텍스트 프롬프트로, 일반적으로 이미지 생성 시에 condition으로 들어가는 값
• z^i_t : timestep t에서 입력 이미지 latent

(\epsilon_\theta-\epsilon)는 예측된 노이즈와 실제 노이즈의 차이를 의미하는데요, 이 차이를 줄이는 방향으로 \phi를 업데이트함으로써 이미지가 diffusion 모델이 원하는 샘플처럼 보이도록 유도합니다. 즉 diffusion 모델에 대한 직접적인 역전파 없이도 \phi를 최적화할 수 있는 것 입니다.

3. Methodology

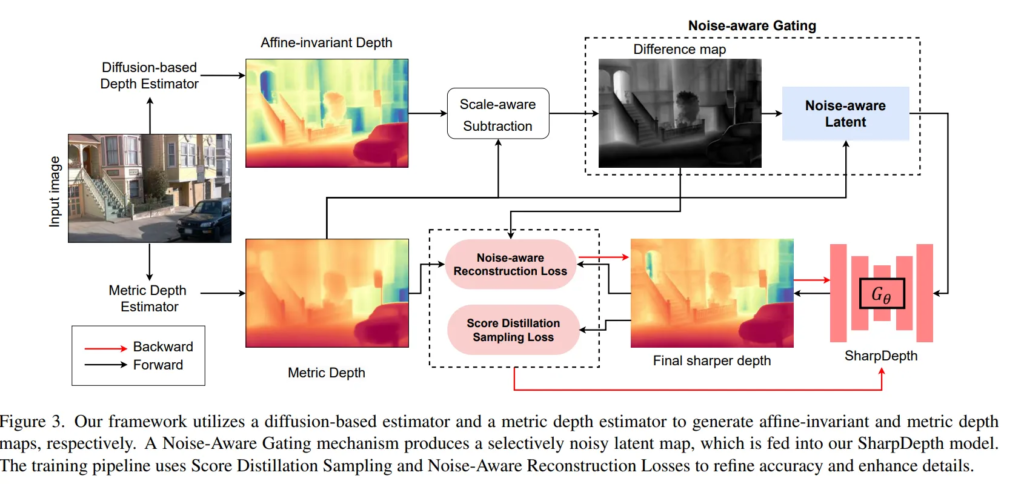
입력 이미지 \mathcal{I}가 들어오면, 사전학습된 metric depth 모델 f_D와 diffusion 기반 depth 모델 f_G에 대해 각각 d, \tilde{d}를 생성 합니다.

여기서 목표하는 바는 제안하는 선명도를 위한 모델 G_\theta를 사용해서 보다 선명해진 metric depth map \hat{d}를 생성하는 것 입니다. 이 모델은 SOTA difusion depth 모델인 LOTUS와 Marigold를 기반으로 한다고 합니다.

diffusion 모델의 forward 과정에 무조건적으로 의존하는게 아니라, 불확실한 영역에 대한 G_\theta에 가이드를 제공하는 노이즈 인지 게이팅 알고리즘을 설계하였습니다. 이는 GT에 의존하지 않고 fine-tuning 할 수 있도록 하기 위해 두 가지 loss 함수를 사용합니다.

우선 SDS loss를 활용하여 사용하여 f_G로부터 미세한 디테일 정보를 distillation하고, Noise-aware Reconstruction loss를 통해 최종 예측된 depth가 기존의 metric depth 예측값과 일치하는 정확도를 유지할 수 있도록 합니다.

3.1. Noise-aware Gating

SharpDepth의 목적은 전체 이미지의 depth를 무작정 다 개선하는게 아니라 개선해야 할 부분만 골라서 처리하는 것 입니다. 이를 위해서는 불확실하거나 부정확한 영역을 찾아내는 것이 먼저겠죠. 그러나 전체 픽셀에 대한 dense한 depth GT를 얻는게 어렵기 때문에 기존 방식들처럼 GT 기반의 학습에만 완전히 의존하기에는 한계가 존재합니다.

그래서 metric depth 예측 모델인 UniDepth와 diffusion 기반 모델이 Lotus를 사용하여 두 모델의 장점을 모두 사용하고자 합니다. 여기서 가정을 하나 하는데요, 두 모델의 예측값 차이가 작으면 그 부분은 둘 다 잘 예측하였기 때문에 신뢰할 수 있는 영역이고, 반대로 차이가 크면 불확실한 영역이라고 가정합니다.

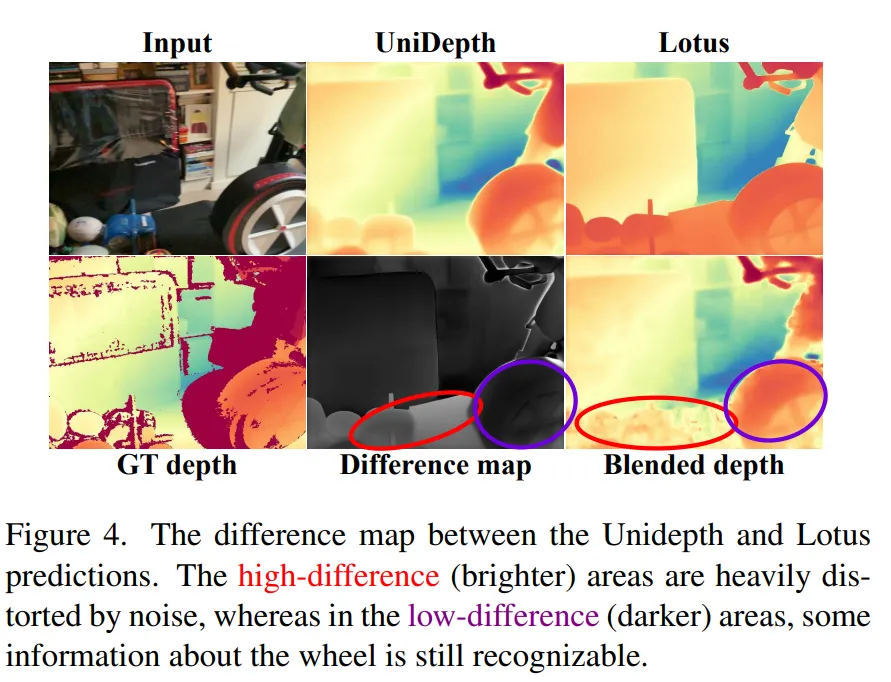
Fig.4를 보면, Unidepth와 Lotus의 출력을 동일한 범위로 정규화를 합니다. 그 다음 동일한 픽셀에서의 차이를 각각 계산해서 difference map을 만듭니다.

이 difference map은 밝은 영역은 두 모델이 예측한 값의 차이가 크기 때문에 개선이 필요하고, 어두운 영역은 거의 동일한 예측이기 때문에 상대적으로 신뢰할 수 있음을 의미합니다. 그래서 밝은 영역역은 개선하기 위해 학습 리소스를 할당하고, 어두운 부분은 그대로 두거나 최소한의 수정만 진행하도록 합니다. 즉, 불확실한 부분에 더 강한 노이즈를 주어 집중적으로 학습할 수 있도록 하는 방식이며, 이를 Noise-aware gating이라고 부르는 것 입니다. Noise-aware Gating을 통해 어떤 부분을 개선해야할 지 결정합니다. 이건 저도 처음 안 부분인데, 최근 diffusion 모델을 활용한 여러 task에서는 관심 있는 영역만 집중적으로 개선하거나 수정하기 위해 마스크를 사용한다고 합니다. 그래서 본 논문도 동일하게, 단순히 이미지 전체에 노이즈를 주지 않고 중요한 영역에만 선택적으로 노이즈를 넣음으로써 학습을 효과적으로 할 수 있도록 합니다. 앞서 이야기한대로 difference map을 만든 다음, 이를 기반으로 차이가 큰 영역에는 강하게 노이즈를 주고, 차이가 작은 영역은 약한 노이즈를 넣거나 또는 거의 노이즈를 주지 않게 됩니다.

difference map을 만드는 방식에 대해 좀 더 얘기해보면, 앞서 정규화를 한다고 이야기했었죠. 예측한 두 depth는 서로 스케일이 다르잖아요. 가령 하나는 0~1 범위가 되고, 다른 하나는 실제 metric depth 값일 수 있기 때문에 직접 비교하면 의미가 없습니다. 이를 해결하기 위해 정규화라고 말했던, 스케일과 shift의 범위를 같은 범위로 맞춰야 합니다. diffusion 모델에서 나온 \tilde{d}에다가 스케일과 shift 파라미터를 통해 d와 동일한 범위에 포함될 수 있도록 합니다. 이렇게 정규화된 두 depth map을 metric depth 값에 대해서 차이를 구하면 그게 difference map이 됩니다.

여기서 특이한 것은 학습이 진행될수록 SharpDepth 모델 G_\theta가 점점 원래의 f_G보다 더 나은 예측을 하게 된다는 것을 실험적으로 발견했다고 합니다. 이 때부터는 사실 f_G는 더 이상의 teacher 역할을 하지 못한다고 판단하고, 그 때부터는 G_\theta의 EMA 버전인 \bar{G}_\theta를 새로운 기준으로 삼는다고 합니다. 이는 단순하게 처음 정한 teacher 모델 하나만 믿는게 아니라 모델이 스스로 점점 teacher가 되어 발전하는 구조이며 일종의 self-distillation에 가까워지게 됩니다. EMA라는건 현재까지의 학습된 모델 파라미터들을 시간에 따라 가중 평균하는 방식인데, 최신 파라미터일 수록 가중치를 더 많이 주고, 오래된 파라미터는 덜 반영하는 방식이라고 합니다.

이렇게 difference map을 얻고 나면, 이제는 어디에 얼마나 노이즈를 넣을지 조절하는게 중요한 부분이 되겠죠. 입력이 앞서 metric depth라고 했는데 다만 이미지 레벨이 아니라 VAE 인코더를 토해 latent 공간으로 변환한 depth이 z_d가 들어갑니다. 수식적으로 보면 식(4)와 같은데요,

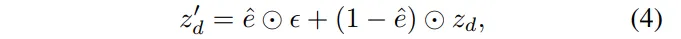
• \epsilon : 가우시안 노이즈
• \hat{e} : difference map e를 latent 크기에 맞추어 다운샘플링한 형태

difference map의 밝은 영역은 \hat{e}의 값이 1에 가까우면서 z’_d가 거의 전부 \epsilon으로 구성되어, 즉 노이즈를 많이 넣어 개선을 유도합니다. 반대로 어두운 영역은 차이가 작은, \hat{e}가 0에 가깝기 때문에 z’_d가 거의 전부 원래의 z_d와 유사한 형태가 되어 기존 정보를 유지하도록 합니다. 즉, 노이즈와 원래의 latent를 섞는 비율을 \hat{e}로 조절하는 방식이라고 할 수 있습니다.

앞서도 계속 이야기하였지만, 이렇게 하는 이유는 식(4)의 출력으로 나오는 z’_d는 모델 G_\theta의 입력으로 들어가는데 강한 노이즈가 들어가면 모델이 복원하려고 집중할 것이고, 노이즈가 없거나 약하면 거의 신경쓰지 않기 때문에 원래의 metric depth 구조를 그대로 유지할 수 있습니다.

3.2. Training Objectives

Diffusion Depth Prior Distillation

이제 학습에 사용하는 두 loss에 대해 살펴볼건데, 첫번째는 SDS loss 입니다.

목적은 diffusion 모델의 knowledge를 G_\theta로 distillation하는 것 입니다. 즉, G_\theta는 처음부터 새로 학습하는게 아니라 이미 잘 학습된 f_G의 출력을 기준으로 삼아 비슷한 출력을 내도록 학습하는 것 입니다.

먼저 앞서 만든 z'_d와 입력 이미지 latent z_i를 G_\theta에 입력으로 넣습니다. 그럼 \hat{z}=G_\theta(z’_d, z_i)의 형태가 되는데, 이 때 \hat{z}는 SharpDepth의 출력 latent로 본 논문에서 학습하고자 하는 대상이 됩니다. 이제 이 \hat{z}를 diffusion 모델에서 원래 쓰이는 방식처럼 노이즈를 부여하여 \hat{z}_t로 만들고, 이걸 다시 f_G에 넣어서 원래 \hat{z}를 얼마나 잘 복워하는지 평가하도록 합니다. 이 때 사용하는 기존의 SDS loss와 다르게 수정된 SDS loss는 식(5)와 같이 정의합니다.

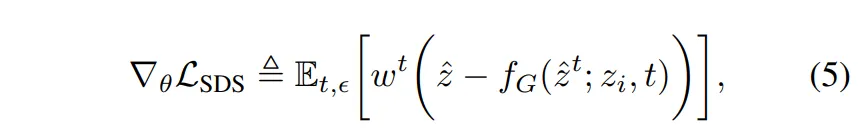
• f_G(\hat{z}_t;z_i,t) : diffusion 모델 f_G가 노이즈를 복원하는 과정
• \hat{z} : SharpDepth의 output
• w_t : timesetp별 가중치

원래의 SDS loss와 달라진 점은 원래 SDS loss는 노이즈를 예측하는 방식이지만, SharpDepth가 사용하는 diffusion teacher 모델은 denoising된 결과를 예측하는 방식이기 때문에 그에 맞춰 비교 대상을 \epsilon이 아니라 복원된 latent \hat{z}로 바꾼 것 입니다.

결국 SDS loss는 SharpDepth의 출력은 diffusion 모델의 결과와 얼마나 일치하는를 계산하는 방식으로, f_G의 출력을 기준으로 G_\theta를 학습합니다.

Noise-aware Reconstruction Loss

SDS loss는 디테일한 영역을 복원하는데 효과적이지만 diffusion 기반 모델의 한계도 같이 따라온다고 합니다. diffusion 기반 모델은 metric 정확도가 낮아서 SharpDepth의 결과는 디테일은 좋아지지만 정확한 거리 추정은 떨어질 수 있는 것 입니다. 이를 해결하기 위한 것이 바로 noise-aware reconstruction loss 입니다. 본 논문의 모델 출력이 diffusion 모델만 따르지 않고 초기 metric depth 모델의 출력 d와도 일정 수준의 유사성을 유지할 수 있도록 유도합니다.

이 loss에서는 단순히 두 depth map 사이의 차이를 계산하는 건 아니고 다시 difference map e를 사용하여 불확실한 영역에만 reconstruction 정도를 높이고자 합니다.

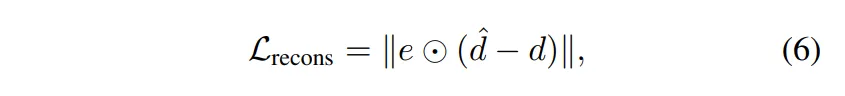
• d : 초기 metric depth

해당 loss를 통해 중요한 부분만, 다르게 말해서 불확실한 영역만을 비교해서 정확하게 학습할 수 있도록 유도하는 것 입니다.

이렇게 두 loss를 같이 사용해서 디테일한 영역은 SDS loss로, 전체 metric한 depth 구조에 대해서까지도 보완할 수 있도록 하였습니다.

4. Experiments

4.1. Experimental Setup

데이터셋에 대해 먼저 보면, 학습에는 여러 데이터셋을 사용하기 위해 각 데이터셋의 약 1%씩을 사용한다고 합니다. 학습에 사용하는 데이터셋은 다음과 같습니다.

• Pandaset, Waymo, ArgoVerse2, ARKit, Taskonomy, ScanNetv2

→ 이는 discriminative depth 모델에 사용된 데이터셋보다 약 100-150배 작은 90,000개의 이미지로 이루어진 학습 데이터를 만들었다고 합니다.

다음 테스트 데이터셋은 아래와 같은 데이터셋을 사용하였습니다.

• KITTI, NYUv2, ETH3D, Diode, Booster, nuScenes, iBims (real 데이터)

4.2. Comparison with the State of the Art

실험에는 4개의 metric depth 모델과 비교한다고 합니다.

(UniDepth, Metric3Dv2, ZoeDepth, 그리고 PatchRefiner)

다만 ZoeDepth는 KITTI와 NYUv2 데이터셋으로 finetuning 된 모델이라 제로샷 모델에는 해당하지 않아서 제로샷 평가에서는 제외하였다고 하네요. 또한 추가적으로 Unidepth-aligned Lotus라는 비교 모델을 선정하였는데요, 이는 Lotus의 예측을 UniDepth의 값 범위로 scale과 shift를 해서 metric처럼 보이도록 만든 모델 입니다.

또한 Marigold, Lotus, BetterDepth라는 zero shot relative depth 모델도 함께 비교하고 있습니다.

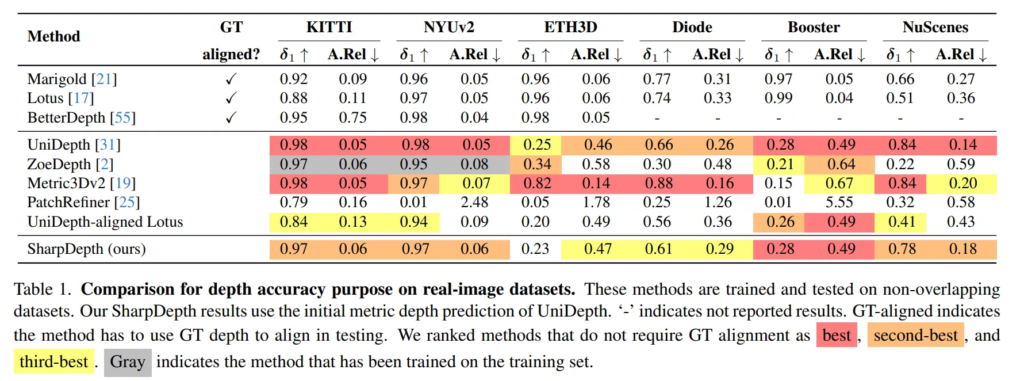
Tab.1을 보면, metric depth 모델과 거의 유사한 정확도를 달성한 것을 확인할 수 있습니다. 이 결과를 통해 결과의 선명함을 위해 확실한 영역은 그대로 유지하면서 불확실한 영역을 선택적으로 집중할 수 있도록 한 것이 효과적이었음을 알 수 있습니다. 또한 UniDepth-aligned Lotus와 비교하였을 때 본 논문이 모든 메트릭과 데이터에서 더 좋은 성능을 보이는데요, 이는 UniDepth의 출력에만 의존하는 것이 최선의 방식이 아니며 difference map을 이용하여 신뢰할 만한 픽셀에 대해서만 align을 맞추고 나머지는 개선하는 과정이 중요함을 어필하고 있습니다.

4.3. Ablation Study

Analysis of Noise-aware Gating

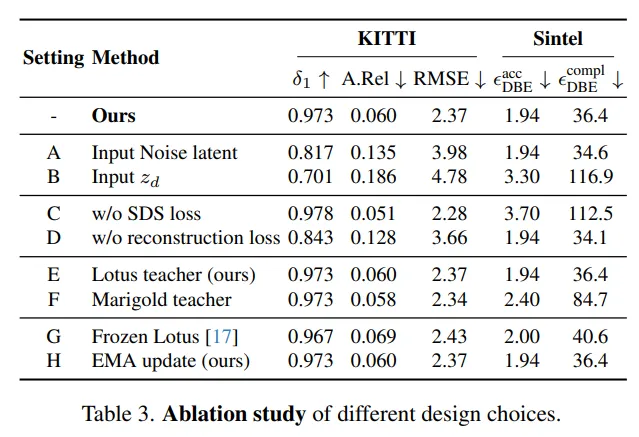
Tab.3은 ablation study 결과를 모아놓은 표 입니다.

우선 noise-aware gating에 대해서는 A-B 세팅을 보시면 됩니다.

제안하는 difference map 대신에 (A) 가우시안 노이즈, (B) 사전학습된 메트릭 depth를 대체 입력으로 넣었을 때를 비교하였습니다. 두 세팅 모두 성능이 저하되는 것을 알 수 있는데, 구체적으로 (A)는 metric depth에 대한 사전 지식이 부족하여 Lotus와 유사하게 작동하게 된 것이라고 분석하였습니다. 두번째 (B)는 metric depth 모델이 유용한 정보를 제공하지만 difference map으로 제공할 수 있는 정보가 부족하기 때문에 reconstruction loss 중에 어떤 영역을 개선해야 할 지 모호해지기 때문에 성능이 저하된다는 것을 알 수 있습니다.

Effects of the Training Objectives

다음 C-D를 통해 학습 loss에 대한 효과를 평가할 수 있습니다.

(C)는 SDS loss를 제외하였는데, distillation loss가 없이도 모델이 f_D에 가까워질 수 있도록 align되어 거의 최종 모델과 유사하거나 더 좋은 예측 결과를 생성합니다. 그냥 metric 모델을 모방하는 방식으로 학습하기 때문에 디테일은 부족하지만 metric 정확도 자체는 높게 평가됩니다. (D)는 reconstruction loss를 제거한 결과로, metric 모델과의 align이 없어서 metric 정확도는 낮지만 diffusion 모델의 디테일은 잘 따라가서 ours와 거의 일치하는 결과를 내는 것을 알 수 있습니다.

Study of Pretrained Teacher Model

다음은 사전학습된 teache 모델에 대한 ablation 결과로, 우선 (E)는 ours랑 동일하다고 합니다. (F)는 Lotus 대신 Marigold를 사용한 결과이구요.

(F)가 depth 정확도가 조금 더 좋지만, (E)는 DBE completion metric에서 50이라는 큰 차이를 두고 높은 세부 정확도를 달성한 것을 알 수 있습니다. 이러한 결과를 통해 Marigold와 Lotus 중 Louts를 디폴트 teacher 모델로 선택하였다고 합니다.

Fig.7의 정성적인 결과만 봐도 Lotus가 더 선명한 엣지를 가지고 정확한 depth를 예측하는 것을 확인할 수 있습니다.