안녕하세요, 65번째 x-review 입니다. 이번 논문은 CVPR 2025년도에 게재된 depth completion 논문으로 Monocular Depth estimation의 결과를 depth completion에 활용한 논문 입니다.
그럼 바로 리뷰 시작하겠습니다 !

1. Introduction
현재 depth completion의 SOTA 모델들은 RGB 이미지와 sparse depth를 같이 사용함에도 불구하고 여전히 기하학적인 fine-grained 디테일 영역들을 표현하는데 어려움이 있습니다. 이는 학습에 사용하는 GT 데이터조차도 sparse한 것에서 나오는 한계인데요, 완전히 dense한 GT 데이터가 아니기 때문에 모델이 전체 scene에 대해서 depth completion을 온전히 학습하는 것이 어려워집니다. 반면에 monocular depth estimation(MDE)에서는 단일 이미지에서 훨씬 dense한 relative depth 예측이 가능하기 때문에, 이를 depth completion에서 유용하게 사용할 수 있을 거라고 가정합니다.
이를 효과적으로 활용하기 위해 본 논문에서는 MDE에서 depth completion 모델로 기하학적인 knowledge를 distillation하는 새로운 2-stage distillation 프레임워크를 제안합니다. 먼저 첫번째 distillation 단계에서는 MDE를 통해 데이터를 만든 다음에 제안하는 사전학습 방식을 통해 knowledge를 distillation합니다. 좀 더 자세히 말해보면 MDE를 통해 pseudo depth map을 만들고, 무작위로 샘플링한 카메라 파라미터를 사용해서 scene을 재구성하여 라이다 데이터를 만드는 것이죠.
그런데 MDE는 relative depth를 예측함에 따라 스케일 모호성이 존재하기 때문에 depth 예측에 있어서 스케일이 달라질 수 있기 때문에 실제 depth라는 신뢰성이 떨어집니다. 그래서 이를 해결하기 위해 두번째 distilltaiton 단계에서 스케일과 sift invariant(SSI) loss를 설계합니다. depth completion 모델이 예측한 depth와 MDE가 예측한 depth가 유사해지도록 학습하되 두 depth 사이의 스케일과 sift는 자동으로 보정할 수 있도록 하였습니다.
이러한 본 논문의 main contribution을 정리하면 다음과 같습니다.
- MDE에서 depth completion으로 knowledge를 전달하는 새로운 2단계 distillation 프레임워크를 제안하여 dense한 depth를 제공함으로써 더 정확한 depth completion 학습이 가능하도록 설계
- 1단계에서는 MDE와 데이터 재구성을 통해 학습 데이터를 시뮬레이션하는 데이터 생성 방식을 제안하여 실제 GT 데이터 없이도 기하학적인 정보를 학습할 수 있도록 제안
- 2단계는 MDE에서의 스케일 모호성을 보완하기 위해 SSI loss를 제안하여 모호한 relative depth에서의 스케일을 일관된 depth completion에 사용할 수 있도록 학습
- KITTI-DC 데이터에서 SOTA를 달성하면서 방법론의 효과를 입증
2. Method
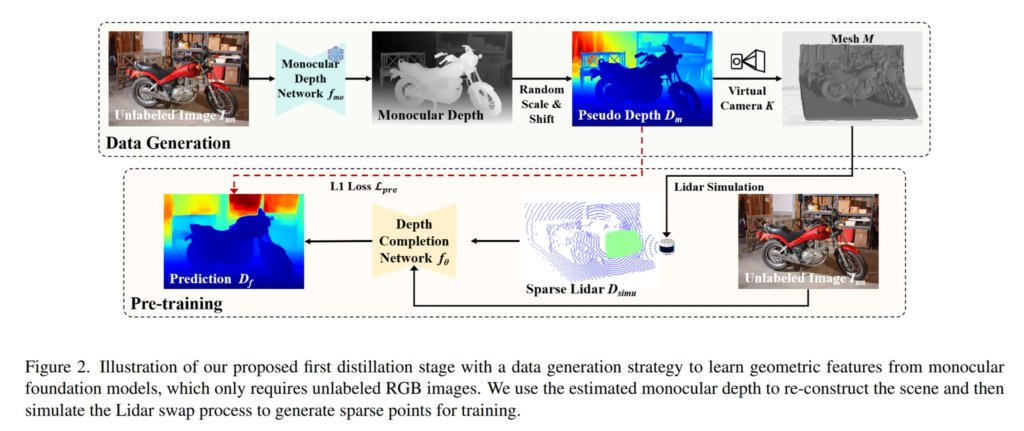
2.1. First Stage: Data Generation and Pre-training
더 많은 학습 데이터를 사용하기 위해 라이다나 GT depth가 없는 일반 RGB 이미지들을 사용하여 MDE를 통해 depth map을 생성합니다. Depth Anything V2와 같은 사전학습된 MDE 모델 f_{mo}를 사용한다고 합니다. 이 결과로 나온 depth map은 절대적인 depth는 아니지만 scene 안에서의 상대적인 depth 구조는 잘 표현하고 있습니다.
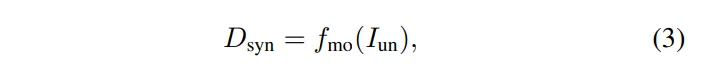
- D_{syn} : dense한 depth map
- I_{un} : RGB 이미지
- f_{mo} : MDE 모델
그 다음에는 실제 라이다 dense map을 대신할 데이터로 만들기 위해 카메라 내부 파라미터를 식(4)와 같이 무작위로 생성합니다.
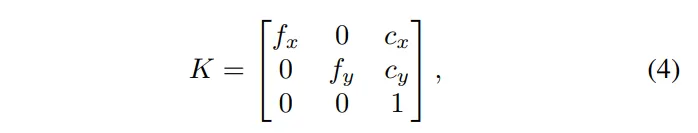
이제 카메라 내부 파라미터가 있으니 예측한 relative depth를 3차원 좌표로 변환할 수 있죠. 각 depth map의 픽셀 (u,v)에는 depth 값 Z가 있으니 내부 파라미터를 통해 3차원 좌표인 (X,Y,Z)를 계산합니다. 이러한 과정을 모든 픽셀에 적용하면 3차원 포인트로 구성된 P=\{(X,Y,Z)\}를 생성하게 됩니다. 이렇게 만든 포인트 집합 P을 재구성을 통해 연속적인 메쉬 형태로 만들었습니다. 이러한 메쉬 형태는 전체가 연결된 3D 구조로 동작하여 시뮬레이션으로 활용할 수 있습니다.
이렇게 메쉬 형태까지 만들었으니 가상의 라이다 센서를 구현해야겠죠.
각 픽셀의 (i,j) 방향으로 가상의 ray d_{i,j}를 쏘는데 이 ray가 메쉬 데이터와 충돌하는 지점까지의 거리를 계산합니다. 그 값을 각 위치의 depth로 저장하는데, 이를 D_{simu}(i,j)로 정의하고 시뮬레이션된 라이다 depth map이 됩니다.
이렇게 만든 depth map을 이용해서 depth completion 모델을 식(5)와 같이 학습합니다.
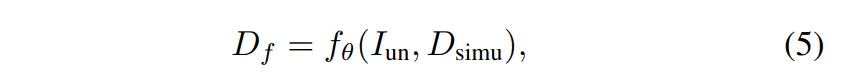
- f_{\theta} : depth completion 네트워크
- I_{un} : 라벨이 없는 일반 RGB 이미지
- D_{simu} : 앞에서 시뮬레이션하여 만들어낸 sparse depth map
- D_f : 예측한 dense depth map
이 depth completion 모델은 아래의 식(6)과 같은 L1 loss로 사전학습 됩니다.
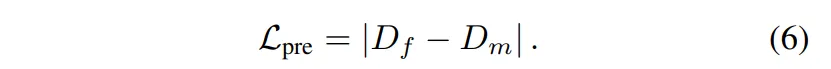
- D_m : MDE가 만든 dense depth map
즉 depth completion이 예측한 depth가 MDE가 만든 dense depth와 유사해지도록 학습합니다.
비록 앞서 이야기하였듯 D_m은 스케일이 정확한 GT depth가 아니지만 상대적인 기하학적 정보를 잘 담고 있기 때문에 D_f가 이와 alignmet가 되도록 학습하는 것 입니다.
2.2. Second Stage: Fine-tuning
앞선 1단계는 사전학습 과정이었고, 이제 GT를 포함한 데이터셋을 사용해서 fine-tuning하는 2단계 입니다.
MDE를 통해 만들어져서 metric 스케일을 알 수 없는 depth map을 기반으로 학습하면 depth completion 모델이 스케일을 잘못 예측할 가능성이 높습니다. 그래서 실제 라이다의 sparse depth와 MDE depth map을 사용해서 2개의 loss를 구성합니다.
첫번째는 식(2)로 정의한 supervised loss 입니다.
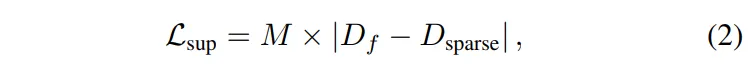
- D_{sparse} : 데이터셋에서 제공하는 sparse GT
- M : valid mask
여기서는 여느 depth completion 네트워크와 동일하게 모델이 예측하는 depth map과 데이터셋에서 제공하는 GT 사이의 loss를 계산합니다.
두번째가 중요한데, 식(7)이 D_m을 적절하게 s(scale)와 b(sift)를 조정해서 모델의 출력과 최대한 비슷하게 만드는 역할을 합니다.
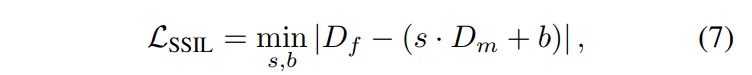
- D_m : MDE의 relative depth
즉, MDE가 전체적인 구조는 맞지만 스케일이 다르기 때문에 그 구조는 따라가되 depth 자체의 스케일과 위치는 무시하도록 설계한 것 입니다. 따라서 D_m에 대해 가장 잘 맞는 s와 b를 따로 찾아서 D_f와의 오차를 최소화하도록 합니다. 모든 픽셀에 대해 D_f와 잘 alignment가 되도록 s와 b를 최적화하여 오차 계산을 함으로써 스케일이나 위치 차이가 아니라 구조 차이만 반영하도록 학습을 하게 됩니다. 이렇게 loss를 설계해서 모델이 상대적인 구조는 잘 따라가면서 스케일이 잘못되었다고 해서 페널티를 주지 않도록 하는 것이죠. 이 loss를 전체 픽셀 단위로 계산되어 실제 학습 때 s와 b를 최적화해서 찾고, 그 상태로 D_f와 s \cdot D_m + b의 차이를 L1로 계산을 하는 것이기 때문에 s와 b는 각 이미지마다 최적화됩니다.
이렇게 설계한 두 loss를 통해 MDE의 구조 정보를 모델이 잘 따르도록 만들 수 있는데, 여기서 단순히 L1 loss를 사용하게 되면 물체의 경계 부분이 흐릿하게 표현될 수 있습니다. 그래서 여느 depth task에서 많이들 설계하는 방식으로 gradient 기반의 loss를 식(8)과 같이 정의하여 함께 사용합니다.
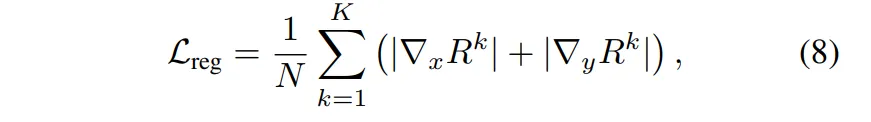
- R : D_f - D_m, 예측 depth와 MDE depth 차이
- R^k : 이미지 해상도를 k 단계만큼 축소한 상태에서의 R
- K=4 : 총 4개의 해상도 레벨
이 loss는 다른 이전에 리뷰했던 논문들에서 사용하는 edge 기반의 loss라고 이해해주시면 되는데요, 예측된 depth map의 gradient가 MDE와 비슷한 형태로 유지될 수 있도록 유도합니다. 물체나 scene 사이에서의 경와 depth의 불연속성이 잘 표현되기 위해서는 depth 값 자체를 잘 예측하는 것도 중요하지만 depth의 변화 정도, 즉 gradient가 유사해야 합니다. 따라서 gradient를 계산하여 모델이 절대적인 depth 값을 예측하면서도 엣지 부분과 같은 영역에서 선명하게 구조가 유지될 수 있도록 도와주는 것이죠.
3. Experiments
3.1. Experimental Pipeline
First Stage
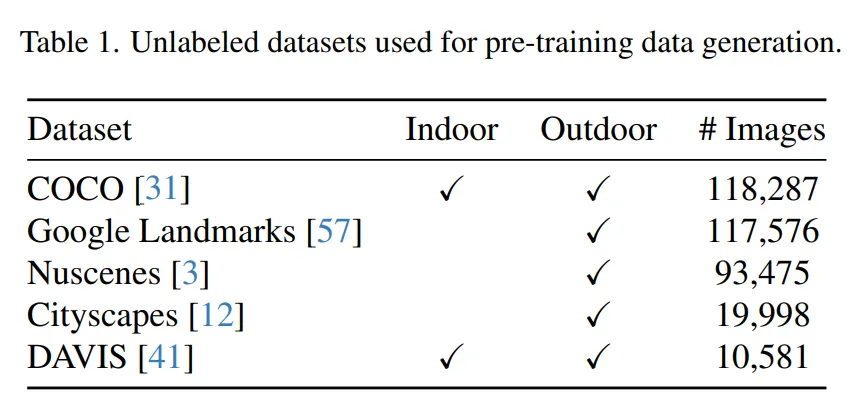
첫번째 단계에서는 method에서 설명한 것과 같이 데이터 생성 방식을 활용해서 depth completion 모델을 scratch 레벨로 사전학습 합니다. Tab.1의 RGB 이미지를 모두 사용해서 depth completion을 위한 시뮬레이션 라이다 데이터를 모두 생성하고, SSI loss만을 사용해서 학습을 하게 됩니다. 이 단계에서는 사전학습된 모델이 라벨링이 된 데이터에 제한되지 않기 때문에 다양한 이미지에서의 기하학적인 특징을 학습함으로써 여러 scene에서의 일반화를 향상시키는 목적으로 수행됩니다.
Second Stage
두번째로는 이제 depth completion을 위한 GT가 존재하는 데이터로 scetion 2.2에서 제안하는 loss를 사용하여 사전학습된 모델을 fine-tuning하는 과정이죠. 여기서 이제 SSI loss를 또 사용하여 MDE 모델에서 depth completion 모델로 distillation하여 metric 단위의 dense depth map을 예측할 수 있도록 합니다. 이 때 fine-tuning에는 KITTI와 NYU Depth v2 데이터를 각각 사용했다고 합니다.
3.2. Comparison with State-of-the-art Methods
Evaluation on Depth Completion Benchmarks
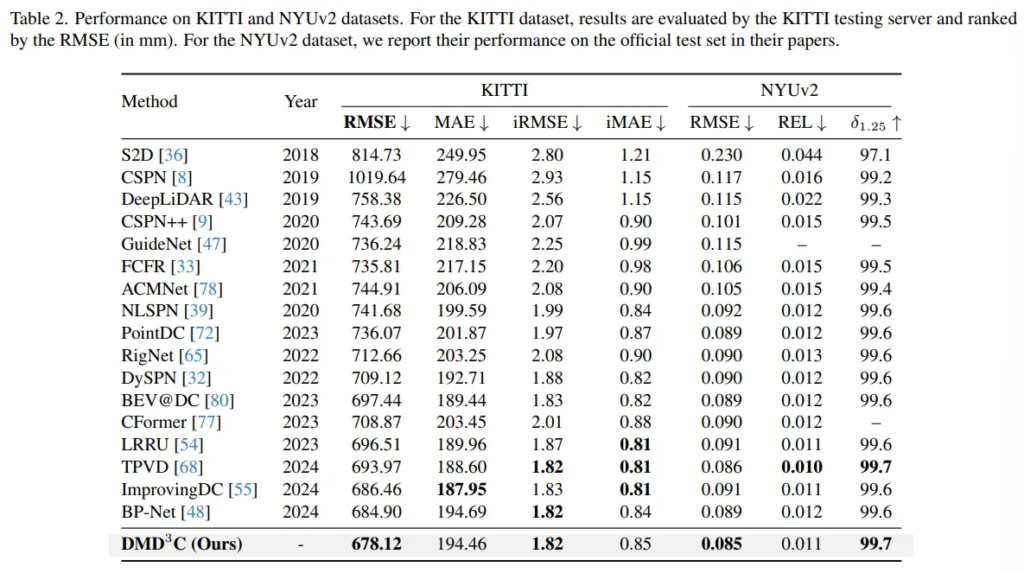

첫번째 실험으로는 KITTI와 NYUv2 데이터에 대해 depth completion을 평가하였습니다. KITTI 데이터에서는 이전의 SOTA, 최신 모델들 대비 RMSE에서 메트릭에서 SOTA를 달성한 것을 확인할 수 있습니다. NYUv2 데이터셋에서도 역시 RMSE에서 좋은 성능을 보이고 있네요. 그런데 KITTI에서의 RMSE를 제외하고는 SOTA를 달성한 메트릭에서도 그렇게 큰 차이는 보이고 있지 않고, 그렇다고 성능을 넘지 못한 MAE 등의 메트릭에서도 크게 하락된 성능을 보이지 않는 매우 유사한 정도의 성능을 보이고 있습니다. 역시나 저자도 SOTA를 달성한 것은 강조하지만 그렇지 못한 평가 메트릭에 대해서도 비슷한 성능을 도달하여 큰 차이가 없다라고 이야기하고 있습니다. 이렇게 좀 더 좋은, 혹은 이전 SOTA와 유사한 정도의 성능을 보이며 강인성과 일반화 가능성을 확인하였다고 분석하고 있습니다.
Fig.4로 정성적으로 보면, 강조된 부분에서 구조가 복잡하거나 다양한 거리에 물체가 있는 scene에서 좀 더 본 논문의 방법론이 더 잘 표현하는 것을 알 수 있습니다. 다른 방법론들도 구조를 아예 표현 못하는 것은 아니지만 본 논문의 방법론이 보다 선명하게 엣지 구조를 유지하고 개별적인 물체들의 depth를 예측하고 있는 것 같습니다
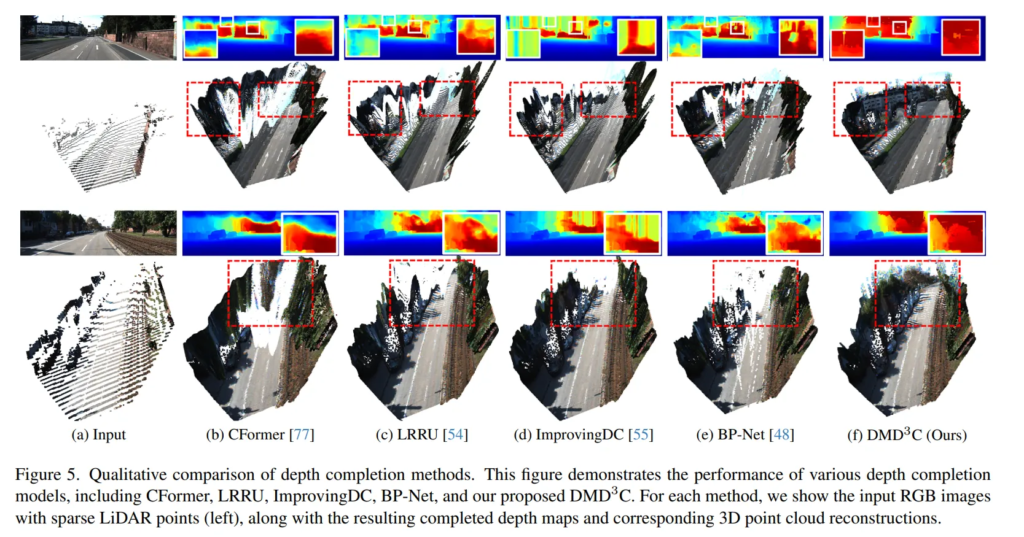
Fig.5의 정성적 결과가 좀 더 어필이 되는 것 같은데요, 최종적으로 예측한 depth map을 포인트 클라우드로 시각화한 결과를 보여주고 있습니다. 확실히 나무의 결이나 뒷쪽 영역들에 대해서 본 논문이 디테일하게 depth를 예측하는 것을 확인할 수 있습니다. 3차원으로의 정성적 결과까지 보이면서 보다 일관성 있게 3차원적인 구조를 생성함으로써 기존 방법론들보다 더 나은 성능을 보일 수 있었다는 것을 보여주고 있습니다.
3.3. Discussions
해당 섹션은 논문에서 제안한 방법들에 대한 ablation study 결과 입니다.
Effect of Pre-training in the First Stage
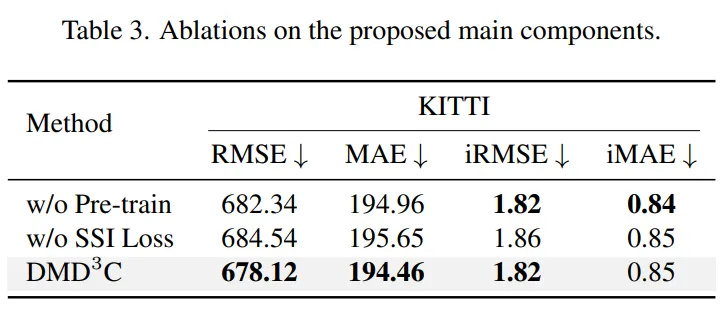
먼저 depth 라벨이 없는 다양한 RGB 이미지를 이용한 사전학습 방식에 대해 비교한 실험 결과 입니다. 이를 위해 사전학습 없이 depth completion 모델을 단순히 처음부터 학습하였다고 합니다. Tab.3을 보면 사전학습 과정인 1단계를 제거하면 RMSE가 약 4.22mm 증가하여 성능이 저하되는 것을 알 수 있는데 이를 통해 사전학습 1단계가 많은 데이터를 이용하여 모델의 일반화 성능을 끌어올려주고 다양한 scene에 대해 복잡한 기하학적 구조를 표현하는데 중요한 역할을 한다는 것을 강조하고 있습니다.
Effect of SSI Loss in the Second Stage
다음은 Tab.3에서 두번째 행에 대한 결과인데요, 사전학습은 논문에서 제안하는대로 그대로 하되, 두번째 distillation 단계에서 SSI loss를 제거하였을 때의 결과를 나타냅니다. 결과적으로 제안하는 SSI loss가 단순히 사전학습하고 depth completion 네트워크를 데이터셋이 제공하는 GT를 사용하여 학습하는 것보다 성능 향상에 도움이 된다는 것을 보여주고 있습니다. 이를 통해 논문에서 가장 강하게 contribution으로 어필하는 만큼 MDE depth를 사용하면서도 절대적인 metric depth 스케일에 맞추도록 설계한 SSI loss가 성능에 크게 영향을 미친다는 것을 알 수 있습니다.
Network Architectures
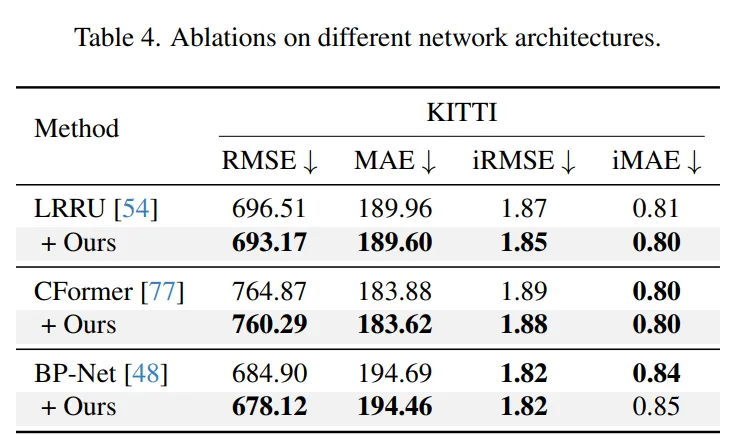
다음은 Tab.4를 통해 여러 기존 네트워크에서의 사용 가능성을 보여주고 있습니다. 학습 방식을 제안한 것이기 때문에 여러 모델에 쉽게 적용할 수 있고 적용했을 때 성능적으로 강인성을 보여준다는 것을 강조하고 있습니다. 실제 결과로도 기존 네트워크 그대로 평가한 것보다 본 논문의 2-stage 학습 방식을 적용했을 때 모두 성능이 향상되는 것을 확인할 수 있습니다.
Generalization to Out-of-Domain Datasets
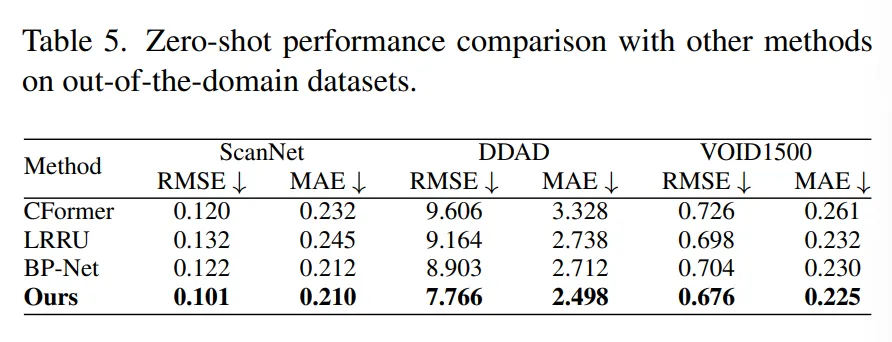
사전학습 단계에서 다양한 이미지를 사용하면서 일반화 성능을 갖출 수 있다고 계속해서 이야기하였는데요, 이를 입증하기 위한 OOD 데이터에 대해 zero shot 성능을 같이 리포팅하고 있습니다.
Tab.5의 ScanNet, DDAD 그리고 VOID1500은 사전학습과 fine-tuning에서 모두 한번도 사용하지 않은 unseen 데이터 입니다. 타 방법론 대비 RMSE와 MAE 메트릭에서 모두 가장 좋은 성능을 보이고 있고, 특히 DDAD 데이터에 대해서 가장 큰 차이를 보이고 있습니다. DDAD 데이터셋도 ScanNet과 마찬가지로 outdoor 데이터인데요, 어떤 차이로 인해서 DDAD에서 특히나 큰 차이를 보이면서 성능 개선이 되었을지에 대해서는 별다른 언급은 없지만 어쨌든 OOD 세팅에서 좋은 결과를 보이면서 주장했던 일반화 성능이 타 방법론들에 비해 잘 이루어졌다는 것을 확인할 수 있는 결과 입니다.