[ICLR 2016] Continuous Control With Deep Reinforcement Learning

안녕하세요, 이번주도 Deep Reinforcement learning 논문을 들고왔습니다. 사실 Deep RL을 적용한 논문을 처음으로 리뷰했을 때 그 논문에 쓰인 알고리즘인데, 그 때는 지식이 너무 부족한 상황이어서 이제서야 해당 알고리즘을 리뷰하게 되었습니다 허허,,

DQN 부터 현재까지의 흐름을 좀 정리해보자면, DQN은 기존 Q-learning을 확장하여 Q-테이블 대신 딥러닝 모델을 사용해 Q-value를 근사하는 방식을 사용한 첫 시도였습니다. DQN 에서 Experience Replay와 Target Network를 도입하여 학습 안정성을 높였고, 이미지와 같은 고차원 data에서도 동작 가능한 강화학습이 가능해졌습니다. 하지만 DQN은 Q-value를 추정할 때 최대값을 선택하는 과정에서 Maximization Bias 문제가 발생하는 한계가 있었고, 이를 해결하기 위해 Double DQN이 등장했습니다. DDQN은 행동 선택과 평가를 분리하여, 온라인 네트워크로 최적 행동을 선택하고 타겟 네트워크로 그 행동의 Q-value를 평가함으로써 Bias를 완화하였습니다. 하지만 DQN과 DDQN은 모두 연속적인 행동 공간에는 최적화가 안 됐다는 한계가 있었습니다. 이번에 리뷰할 논문은 연속적인 행동 공간에서도 학습할 수 있도록 개발된 DDPG(Deep Deterministic Policy Gradient)라는 알고리즘을 소개하는 논문입니다.

DDPG는 지금껏 리뷰했던 논문들과는 다른 Actor-Critic 구조를 기반으로 하며, Actor(액션)가 연속적인 행동을 직접 출력하고, Critic은 해당 행동의 Q-value를 평가하는 방식으로 작동합니다. DDPG 역시 Experience Replay와 Target Network를 활용하는 알고리즘 입니다. 요약하자면 Q-Learning 부터 각종 문제들을 해결해나가면서 연속적인 공간에서의 RL 까지 가능해진 상황이 왔고, joint position과 같이 연속적인 제어가 필수인 manipulator 제어를 위한 강화학습 기법의 시작이라고 보시면 될 것 같습니다. 결과적으로도 하나의 동일한 학습 알고리즘, 신경망 구조, 하이퍼파라미터를 사용하여 카트폴, 로봇팔 조작, 보행 로봇, 자동차 주행 등 기존에 해결하지 못 하던 20가지가 넘는 다양한 시뮬레이션 물리 문제를 해결했다고 합니다. 이제 더 자세하게 알아보도록 하겠습니다.

Background

Actor-Critic

Actor-Critic 구조도 Q-learning 과 같이 주어진 상태에서 어떤 행동을 하는것이 가장 유리한지를 학습합니다. 다만 Q-learning에서 특정 상태에서 어떤 행동을 했을 때의 return을 가지고 학습 할 때, 가능한 모든 행동들을 비교해가며 값을 업데이트 하기 때문에, 가능한 행동이 무한대인 경우(연속적인 공간)에서는 문제가 발생합니다. 무한대로 많은 경우의 수에 대해서 Q값을 전부 계산할 수 없기 때문입니다. 그렇기 때문에 Actor, Critic 네트워크를 따로 만들어서 사용합니다. Actor는 Policy 자체를 의미합니다. 주어진 상태 s에서 직접 a를 출력하는 네트워크이고, 이 때의 (s,a)쌍을 입력으로 Q(s,a)를 예측하는 알고리즘이 Critic 네트워크 입니다. DQN 처럼 여러 Q(s,a)들 중 최댓값을 선택할 수 없기 때문에, Q function을 학습하는 것이 아니라 Policy 자체를 학습해서 action을 출력하는 네트워크 Actor, 가치를 평가하는 네트워크 Critic을 따로 두는 것입니다. 요약하자면, Q function만을 학습하는것에 반해 policy 와 value 자체를 둘 다 학습한다고 보시면 될 것 같습니다.

DPG – Deterministic Policy Gradient

DDPG라는 알고리즘의 이름이 Deep DPG인 만큼 DPG의 개념에 대해서도 정리하고 가도록 하겠습니다. DQN과 DDQN 방법들은 주어진 상태에서 어떤 행동이 가장 높은 가치를 갖는지를 학습하여 최적의 행동을 ‘선택’하는 방식이었습니다. 특히 discrete한 행동 공간에서 모델링 했습니다. 하지만 앞서 말했듯 세상의 많은 문제들은 연속적인 행동 공간을 가지고 있고, 이런 환경에서는 가능한 모든 행동에 대한 Q-값을 계산하고 그중 최댓값을 찾는 연산이 불가능합니다.

이 문제를 해결하기 위한 접근법 중 하나가 Policy Gradient 방법입니다. Policy Gradient에서는 Q-function를 통해 간접적으로 행동을 선택하는 대신, 정책 π 자체를 직접 학습합니다. 정책 π는 주어진 상태 s에서 어떤 행동 a를 할지를 결정하는 함수 또는 확률 분포입니다. Policy gradient의 목표는 기대되는 총 보상을 최대화하는 방향으로 정책의 파라미터 θ를 업데이트하는 것입니다. 즉, ∇θ​J(θ)를 계산하여 gradient ascent를 사용합니다.

일반적인 Policy Gradient 알고리즘들은 주로 확률론적 정책 π(a∣s;θ)를 사용합니다. 이는 상태 s가 주어졌을 때 행동 a를 선택할 ‘확률’을 출력합니다. 이 확률 분포에 따라 행동을 샘플링하여 환경과 상호작용하고, 얻어진 보상을 바탕으로 좋은 결과를 낸 행동의 확률은 높이고, 나쁜 결과를 낸 행동의 확률은 낮추는 방향으로 정책 θ를 업데이트합니다. 확률론적 정책의 경사는 보통 아래과 같은 형태로 나타납니다.

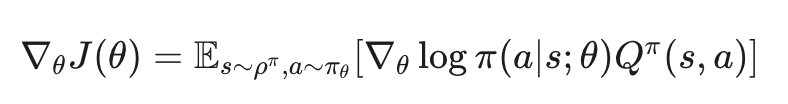
여기서 logπ(a∣s;θ) 항 때문에 확률적인 샘플링이 필요하고, 이로 인해 그래디언트 추정치의 variance가 커지는 문제가 발생할 수 있습니다. 따라서 Deterministic Policy Gradient는 확률 분포를 출력하는 대신, 주어진 상태 s에 대해 하나의 특정 행동 a를 직접 출력하는 Deterministic Policy μ(s;θ)를 사용합니다. 결정론적 정책 μ(s;θ)의 파라미터 θ에 대한 목적 함수 J(θ)의 그래디언트는 아래와 같이 표현될 수 있습니다.

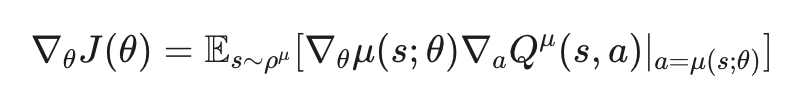
액터가 어떤 행동 μ(s;θ)를 출력했을 때, 크리틱이 그 행동을 조금 바꾸면 Q-값이 증가할 것이라고 알려주면(∇a​Q>0), 액터는 그 방향으로 행동을 출력하도록 파라미터 θ를 조정하라(∇θ​μ를 따라 업데이트)는 의미로 해석할 수 있습니다. Actor의 행동이 Critic을 통해 개선되는 방향입니다. 이러한 Deterministic Policy는 샘플 효율성과 계산 효율성 크게 증가시킨다고 합니다. 갑자기 Actor Critic이 나와서 추가로 설명을 하자면 Determiniscit Policy Gradient의 구조에서 Deterministic Policy 자체를 학습하는 네트워크가 Actor이고, Q(s,a)를 학습하는 네트워크가 Critic 역할을 하게 됩니다.

DDPG – Deep Deterministic Policy Gradient

Algorithm

DDPG는 위에 설명한 DPG 이론을 기반으로, Actor와 Critic을 Deep Neural Network로 구현하고, DQN에서 사용된 경험 리플레이Experience Replay와 Target Network 기법을 결합하여 안정성과 성능을 높인 model-free, off-policy, actor-critic 알고리즘입니다. 우선 저자는 DPG에서 deep neural network을 사용하면 이론적인 수렴성이 보장되지 않았다고 합니다. 하지만 대규모 상태 공간에서 효과적으로 학습하고 일반화하기 위해서는 강력한 Approximator(DQN과 DDPG 모두 DNN을 활용했습니다)가 필수적이라고 합니다. 과거의 연구인 NFQCA는 DPG와 동일한 업데이트 규칙을 사용하고 신경망 함수 근사기를 적용했지만, 안정성을 위해 batch learning을 사용했다고 합니다. 그러나 batch learning 대규모 네트워크에서는 실용적이지 않은 방식이기 때문에 minibatch 방식으로 수정하고 매 업데이트마다 정책을 초기화하지는 않음으로써 본질적으로 DPG 알고리즘과 동일한 알고리즘을 구현했다고 합니다.

저자는 핵심 Contribution이 여기에 있다고 합니다. 연구진은 DQN의 성공 사례를 통해 DPG 알고리즘에 DNN을 결합해 Large State Space와 Action Space에서 online으로 학습하는 것이 가능해졌다고 합니다. 다만 여기서 신경망을 강화학습에 사용할 때 주요 문제들 중 하나는 대부분의 최적화 알고리즘은 샘플들이 독립적이고 동일하게 분포되어 있다고 가정한다는 점이라고 합니다. 하지만 강화학습에서의 데이터는 환경을 순차적으로 탐험하면서 생성되는 샘플들은 강한 시간적 상관관계를 가지므로 이 가정을 만족하지 못합니다. 이와 더불어 하드웨어 최적화 기법을 효율적으로 활용하기 위해서는 온라인 방식보다는 미니배치 단위로 학습하는 것이 필수적이었다고 합니다.

DQN에서와 마찬가지로, DDPG는 이러한 문제들을 해결하기 위해 replay buffer를 사용합니다. Buffer는 유한한 크기를 가지는 메모리 R입니다. exploration policy에 따라 환경과 상호작용하면서 얻는 transition 정보, 즉 <st​,at​,rt​,st+1​> 튜플이 replay buffer에 순차적으로 저장됩니다. 버퍼가 가득 차면 가장 오래된 샘플부터 폐기됩니다. 매 time step마다 actor와 critic을 업데이트하기 위해, 버퍼에서 무작위로 uniform 하게 미니배치 크기만큼의 transition들을 추출합니다. DDPG는 off-policy 알고리즘이기 때문에, 현재 정책과 다른 과거의 정책으로부터 생성된 데이터를 학습에 사용할 수 있습니다. 이를 통해 알고리즘은 시간적으로 상관관계가 없는 다양한 전이 데이터 집합으로부터 학습하는 이점을 얻을 수 있었다고 합니다. (사실 이 부분은 DQN의 replay buffer 개념과 완전 일치하는 것 같습니다.)

추가적으로 단순히 Q-러닝의 업데이트를 신경망에 직접 적용하는 것은 많은 환경에서 학습이 불안정해지는 결과를 낳았다고 합니다. 업데이트되는 네트워크 Q(s,a∣θ)가 타겟 값 yt​=r(st​,at​)+γQ(st+1​,μ(st+1​)∣θQ) 계산에도 사용되기 때문에, Q 업데이트 과정이 발산하기 쉬운 경향이 있었다고 합니다. 이 문제를 해결하기 위해 저자들은 DDPG의 접근 방식을 DQN에서 사용된 target network와 유사하지만 actor-critic 구조에 맞게 수정하고, 가중치를 직접 복사하는 대신 soft target update 방식을 사용했다고 합니다. 구체적으로, 타겟 값을 계산하는 데 사용될 Q′(s,a∣θQ′)와 μ′(s∣θμ′) (복사본들 입니다)를 생성하고, 이 타겟 네트워크들의 가중치는 학습 중인 메인 네트워크들의 가중치를 서서히 추적하도록 업데이트 했다고 합니다. 업데이트 규칙은 θ′←τθ+(1−τ)θ′ 이며, τ는 보통 0.001과 같은 매우 작은 값을 활용했다고 합니다. 이 방식을 통해 target value가 천천히 변하도록 제약되어 학습의 안정성이 크게 향상됐다고 합니다. 이러한 변경을 통해 action-value 학습이라는 비교적 불안정한 문제를, 안정적인 해법이 존재하는 supervised learning 문제에 더 가깝게 만들 수 있었다고 합니다. 연구진은 안정적인 타겟 값 yi​를 얻고 Critic이 발산하지 않고 일관되게 학습되기 위해서는 타겟 액터 μ′와 타겟 크리틱 Q′가 모두 필요하다고 주장합니다. 타겟 네트워크는 가치 추정치의 전파를 지연시켜 학습 속도를 늦출 수도 있지만, 실제로는 학습 안정성 향상이라는 이점이 훨씬 더 크다는 것을 확인했다고 합니다.  

또 low-dimensional feature vector 관측값을 사용하여 학습할 때, 관측값의 각 요소는 서로 다른 물리적 단위를 가질 수 있으며, 그 범위도 환경에 따라 크게 다른 문제를 확인할 수 있었다고 합니다. 이는 네트워크가 효과적으로 학습하기 어렵게 만들 수 있으며, 다양한 환경에 걸쳐 일반화될 수 있는 하이퍼파라미터를 찾기 어렵게 만들었다고 합니다. 저자들은 이 문제에 대한 햅버으로 특징 값들이 환경과 단위에 걸쳐 유사한 범위에 있도록 수동으로 스케일링하는 것을 택했다고 합니다. 저자들은 이러한 문제를 해결하기 위해 Batch Normalization를 적용했습니다. 또한, inference를 진행할 때 정규화를 위해 평균과 분산의 running average를 유지했다고 합니다. 심층 신경망에서는 각 층이 whitened 입력을 받도록 보장함으로써 학습 중 covariance shift를 최소화하는 데 사용된다고 합니다. 저차원 특징 벡터를 사용하는 경우, DDPG에서는 상태 입력과 액터 네트워크의 모든 은닉층, 그리고 크리틱 네트워크에서 행동 입력이 들어오기 전까지의 모든 은닉층에 배치 정규화를 적용했습니다. 저자들은 배치 정규화를 사용함으로써 각 단위들이 특정 범위 내에 있도록 수동으로 조정할 필요 없이, 다양한 유형의 단위를 가진 여러 다른 작업에서 효과적으로 학습할 수 있었다고 합니다.

DQN의 장점을 살리면서 연속 행동 공간에서 학습할 때 또 해결해야 할 포인트는 exploration이었다고 합니다. DQN에서는 epsilon-greedy 정책을 사용해 exploration을 진행했습니다. DDPG 역시 exploration 개념이 적용돼있는데, DDPG와 같은 오프-폴리시 알고리즘의 장점 중 하나는 탐험 문제를 학습 알고리즘과 독립적으로 다룰 수 있다는 점었다고 합니다. 저자는 exploration 정책 μ′를 Actor 정책 μ(st​∣θtμ​)에 노이즈 프로세스 N로부터 샘플링된 노이즈를 추가하여 구성했습니다. 확률적으로 random하게 액션을 선택하게 하는 방식과 달리 복사된 policy에 임의로 아래와 같이 gaussian noise를 추가했다고 합니다.  

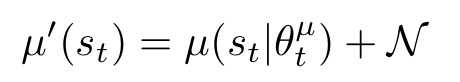
노이즈 N은 환경의 특성에 맞게 선택될 수 있다고 합니다. 관성(inertia)이 있는 물리 제어 문제에서 탐험 효율성을 높이기 위해, 논문에서는 시간적으로 상관관계가 있는 노이즈를 생성하는 Ornstein-Uhlenbeck 프로세스를 사용했다고 합니다. 이 프로세스는 마찰이 있는 브라운 입자의 속도를 모델링해서, 결과적으로 0을 중심으로 시간적 상관관계를 갖는 노이즈 값을 생성한다고 합니다. 저도 이해가 안 돼서 조금 찾아봤는데, 쉽게 말하자면 평균 회귀(mean-reverting) 성질을 가진 랜덤 노이즈인 것 같습니다. 서로 시간적으로 연관되어있고, 평균에서 멀어지면 다시 평균으로 회귀하는, 평균으로 당기는 성질을 가졌다고 합니다. 이는 로봇 팔 제어와 같이 관성이 있는 물리 시스템에서는 행동이 갑자기 크게 변하는 것보다 부드럽게 변하는 것이 더 현실적이고 효과적인 탐험이 될 수 있기 때문에 채택했다고 합니다. 아래와 같은 확률 미분 방정식으로 표현되고, OU 프로세스 Xt​의 다음 순간 변화량(dXt​)은 현재 값이 평균(μ)에서 벗어난 정도에 비례하여 평균 쪽으로 돌아가려는 힘(θ(μ−Xt​)dt)과 랜덤한 노이즈(σdWt​)의 합으로 결정된다고 합니다.

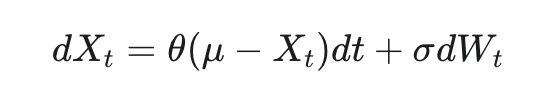
DPG에 기반한 Actor-Critic 구조, Replay Buffer, 소프트 업데이트를 사용하는 Target Network, Batch Norm, Noise로 표현된 exploration까지 결합되어 DDPG 알고리즘을 형성하며, 이를 통해 연속적인 행동 공간을 가진 복잡한 제어 문제를 효과적으로 학습할 수 있게 됐다고 합니다. 알고리즘의 전체적인 흐름은 아래 Algorithm 1 수도코드를 통해 확인해볼 수 있습니다. 초기화 단계에서는 Actor, Critic 네트워크 및 해당 Target 네트워크들을 초기화하고 Replay Buffer를 선언합니다. 이후 각 에피소드마다 exploration을 위한 노이즈 프로세스를 초기화하고 환경과 상호작용을 시작합니다. 매 timestep t마다 현재 policy와 exploration 노이즈를 결합하여 액션 at​를 선택하고, 이 액션을 실행하여 보상 rt​와 다음 상태 st+1​을 관찰합니다. 관찰된 transition(st​,at​,rt​,st+1​)은 Replay Buffer(R)에 저장됩니다. 그런 다음, R에서 N개의 transition sample로 구성된 미니배치를 무작위로 추출합니다. 이 미니배치를 사용하여 타겟 값 yi​=ri​+γQ′(si+1​,μ′(si+1​∣θμ′)∣θQ′)를 계산하고, 이 타겟 값과의 MSE를 최소화하여 Critic 네트워크를 업데이트합니다. 마지막으로, 샘플링된 Policy Gradient​​를 사용하여 Actor 정책을 업데이트하고, soft 업데이트 규칙에 따라 Target Network들의 가중치를 업데이트합니다. 이 과정이 에피소드가 끝날 때까지, 그리고 총 M 에피소드 동안 반복됩니다.

Results

저자들은 다양한 난이도의 시뮬레이션 기반 물리 환경들을 구축하여 실험을 수행했습니다. 실험 환경에는 cartpole과 같은 전통적인 강화학습 문제뿐만 아니라, gripper와 같은 고차원 과제, puck striking과 같이 충돌 및 접촉이 포함된 과제, 그리고 cheetah와 같은 이동과제 등 더 어렵고 복잡한 문제들도 포함되었다고합니다. cheetah 환경을 제외한 모든 환경에서 에이전트의 action은 작동되는 관절에 가해지는 토크값으로 정의되었습니다. 환경들은 아래와 같이 MuJoCo 물리 엔진을 사용하여 시뮬레이션 했다고 합니다.

저자는 모든 실험에 대해 두 가지 다른 형태의 observation을 사용하여 실험을 진행했다고 합니다. 첫 번째는 관절 각도나 위치와 같은 low-dimensional state 정보를 직접 사용하는 방식이고, 두 번째는 환경을 렌더링한 high-dimensional renderings 정보를 직접 사용하는 방식이었다고 합니다. DQN 논문에서와 유사하게, 고차원 환경에서 문제를 거의 fully observable하게 만들기 위해 action repeats 기법을 사용했다고 합니다. 에이전트가 한 번의 timestep을 결정하면, 시뮬레이션은 해당 행동을 3번 반복하며 3 timestep 동안 진행되고 각 step마다 환경을 렌더링합니다. 따라서 에이전트에게 전달되는 관측 정보는 총 9개의 feature map으로 구성됩니다(3개의 렌더링 프레임 각각의 RGB 채널). 이를 통해 에이전트는 프레임 간의 차이를 이용하여 속도와 같은 동적인 정보를 추론할 수 있는 구조라고 합니다. 입력 이미지는 64×64 픽셀로 다운샘플링되었고, 8비트 RGB 값은 0과 1 사이의 부동 소수점 값으로 변환되었습니다. 모델은 공통적으로 ReLU를 activation으로 사용한 3층의 CNN구조와 2층의 fc layer로 구성됐다고 합니다.

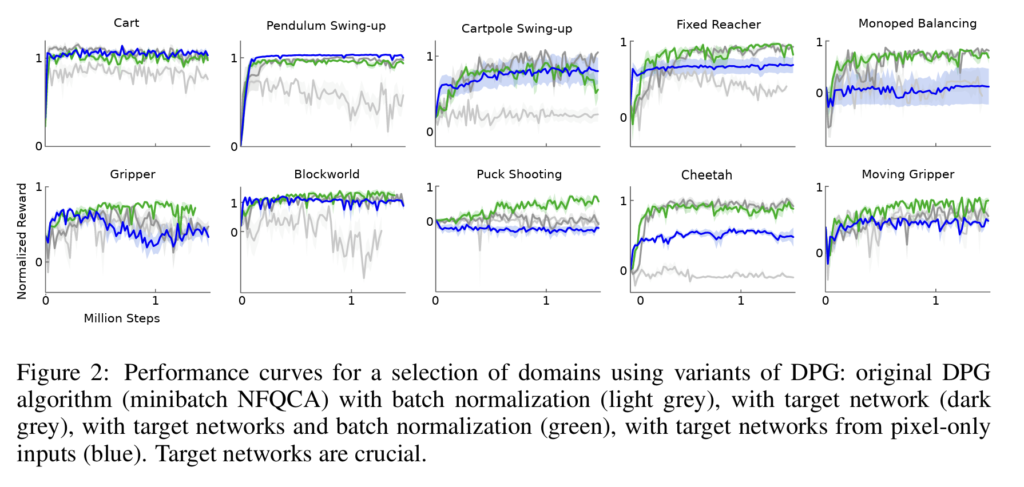
알고리즘의 성능 평가는 학습 과정 중에 주기적으로 이루어졌으며, 평가 시에는 exploration noise를 제거한 상태에서 정책을 테스트했다고 합니다. 아래 figure는 일부 선택된 환경에서의 성능 변화 곡선을 보여줍니다. 아래 그래프는 Target Network 없이 Batch Norm만 사용한 버전, Target Network만 사용한 버전 , 모두 사용한 버전 , 그리고 픽셀 입력과 Target Network를 사용한 버전입니다. 결과를 통해 알 수 있듯이, 모든 과제에서 좋은 성능을 달성하기 위해서는 Target Network와 Batch Norm은 모두 필수적이었다고 합니다. 특히, 기존의 DPG 연구처럼 타겟 네트워크 없이 학습하는 경우, 많은 환경에서 성능이 매우 저조하다고 합니다. 일부 비교적 간단한 과제에서는 pixel image로부터 직접 정책을 학습하는 속도가 low dimension 정보를 통해 학습하는 속도만큼 빠른 경우도 관찰되었는데, 저자는 이것이 행동 반복 기법이 문제를 더 단순하게 만들었기 때문일 수도 있고, CNN을 통한 feature가 상태 공간을 쉽게 분리 가능한 표현으로 변환하여 상위 레이어들이 빠르게 학습할 수 있었기 때문일 수도 있다고 추측했습니다.  

저자는 학습 후 DDPG의 Critic 네트워크 Q가 추정한 return과 실제 테스트 에피소드에서 관찰된 GT return을 비교하여 DDPG의 가치 추정 정확도를 경험적으로 조사했다고 합니다. 아래 figure의 density plot을 통해 확인할 수 있습니다. pendulum 이나 cartpole과 같은 간단한 과제에서는 DDPG가 체계적인 편향 없이 꽤 정확하게 반환값을 추정하는 것을 볼 수 있었다고 합니다. 더 어려운 과제에서는 Q 추정치의 정확도가 떨어지지만, 그럼에도 불구하고 DDPG는 여전히 우수한 정책을 학습하는 데 이 추정치를 효과적으로 사용할 수 있었다고 합니다.

Conclusion

대부분의 강화학습 알고리즘과 마찬가지로, DDPG 역시 비선형 approximator를 사용하기 때문에 이론적인 수렴성이 보장되지는 않는다고 합니다. 주목할 만한 점은, 본 논문의 모든 실험에서 문제 해결에 사용된 experience의 수가 DQN이 아타리(Atari) 게임 영역에서 해답을 찾는 데 사용했던 것보다 현저히 적었다는 사실이라고 합니다. 연구진이 다룬 거의 모든 문제들은 250만 스텝 이내의 경험(대부분의 경우 250만 보다 훨씬 더 적은 스텝)으로 해결되었는데, 이는 DQN이 아타리 게임에서 좋은 성능을 보이는 데 필요한 스텝 수보다 약 20배나 적은 수치였다고 합니다.

다만 그럼에도 불구하고, 제안된 접근 방식에는 몇 가지 한계점이 여전히 남아 있다고 합니다. 가장 두드러진 한계점은 대부분 model-free 강화학습과 마찬가지로, DDPG 역시 해답을 찾기 위해 상당한 수의 학습 에피소드(training episodes)를 필요로 한다는 것입니다. 하지만 저자는 이러한 한계점에도 불구하고, 안정적인 모델 프리 접근법이 이러한 한계점들을 극복하기 위한 더 큰 시스템의 중요한 구성 요소가 될 수 있을 것이라고 믿습니다. (저도 이건 model free 아니면 거의 불가능 하기 때문에 그래도 괜찮지 않나 싶긴 합니다..) 결론적으로, 이 연구는 DDPG라는 알고리즘을 토대로 향후 복잡한 제어 문제 해결을 위한 중요한 기반을 마련했다고 평가할 수 있다고 합니다. 실제로 해당 연구 이후 TD3나 HER과 결합한 DDPG등 많은 연구들이 진행된것을 확인할 수 있었습니다.