안녕하세요, 이번주도 저번주에 이어서 강화학습에 딥러닝을 적용한 논문을 리뷰해보도록 하겠습니다. 강화학습에 처음으로 딥러닝을 적용한 DQN이 가지고 있는 Q-value 과대추정(overestimation bias) 문제를 해결하기 위해 제안된 알고리즘입니다. 특정 조건에서 action value를 과대평가하는 경향이 있다고 알려진 Q Learning에서 과대평가가 실제로 자주 발생하는지, 성능에 어떤 영향을 미치는지, 그리고 이를 일반적으로 방지할 수 있는지는 명확히 밝혀지지 않았다고 합니다. 이번 논문에서는 이러한 명확하지 않은 부분들을 해결했습니다. 제안된 알고리즘은 예상대로 과대평가를 줄이는 동시에, 여러 게임에서 성능 향상도 함께 이끌어냈다고도 합니다. 자세히 살펴보도록 하겠습니다.
Background
DQN
앞서 DQN 리뷰에서도 Q-learning에 대한 이야기를 다루기는 했지만 필요한 내용들을 정리해보도록 하겠습니다.
순차적인 의사결정 문제를 해결하기 위해서는 각 상태에서 가능한 행동의 가치 함수를 학습해야 합니다. 가치 함수란 특정 상태에서 어떤 행동을 선택하고, 이후 최적의 정책을 따른다고 가정했을 때 기대되는 미래 보상의 총합을 의미합니다. 특정 정책 π 하에서 상태 S에서 행동 A의 action value는 다음과 같이 정의됩니다.
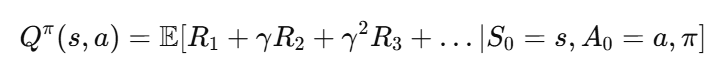
여기서 γ는 현재 보상과 미래 보상 사이의 균형을 조절하는 할인율(discount factor)입니다. 최적의 정책을 따를 경우의 가치, 즉 최적 행동 가치 함수는 모든 정책 중 최대 기대 보상인 a를 행하는 형태로 정의됩니다.
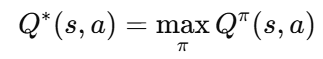
하지만 이전의 DQN 논문에서 말했듯 대부분의 현실 세계의 문제는 상태 공간이 너무 커서 상태-행동 쌍마다 별도로 값을 저장하는 것이 불가능하기 때문에, 신경망 등으로 파라미터화된 함수 Q(s,a;θt)를 활용해 다음과 같이 업데이트 해나갑니다. 모든 에피소드를 확인 할 수 없기 때문에 이 때 에이전트가 환경과 상호작용한 내역을 버퍼에 저장하고 샘플링하면서 업데이트 하고, 이 때 별도의 Target Network를 사용해서 안정성을 높였습니다.
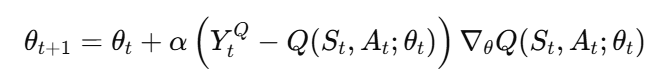
이 때 α는 학습률, Y_t^Q는 학습의 목표인 타겟 값으로, 같고 DQN의 Target Network의 경우 아래의 Y^DQN을 사용합니다.
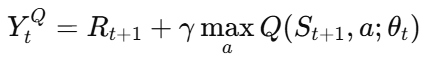
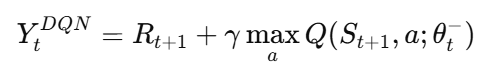
정리하자면 DQN은 현재의 가치 예측이 미래의 최대 기대 보상에 얼마나 가까운지를 반영하며 SGD 형태로 업데이트가 수행됩니다.
Double Q-Learning
Q-learning 및 DQN에서는 타겟 값을 계산할 때 같은 Q함수로 행동을 선택하고 평가합니다. 다시 말해, 최대 Q값을 선택하기 위해 사용한 함수로 그 값 자체를 평가하기 때문에, 과대평가된 행동이 선택될 가능성이 높아집니다. 이로 인해 전반적으로 행동 가치가 과도하게 낙관적으로 추정되는 문제가 발생할 수 있다고 합니다.
이를 해결하기 위한 접근이 바로 Double Q-learning입니다. 핵심 아이디어는 행동 선택(selection)과 행동 평가(evaluation)를 분리하는 것입니다. 원래의 Double Q-learning 알고리즘에서는 두 개의 Q함수를 유지하며, 각 경험을 무작위로 한 Q함수에 할당해 업데이트합니다. 따라서 Double Q-learing에서는 Y를 다음과 같이 나타냅니다.
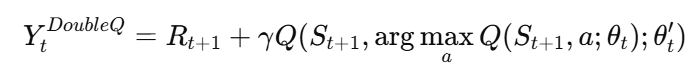
조금 정리를 해보자면… 기존 Q-learning과 DQN에서는 가장 좋은 행동을 고를 때도, 그 행동의 가치를 평가할 때도 같은 Q함수를 사용합니다. 이렇게 되면 실제보다 과도하게 낙관적인 예측이 반복되면서, 전체 정책이 왜곡될 수 있습니다. Double Q-learning은 이 문제를 선택과 평가를 다른 Q를 활용해서 해결합니다. 하나의 네트워크는 가장 좋아 보이는 행동을 고르고, 다른 네트워크는 그 행동이 진짜로 좋은지 평가합니다. 이러한 컨셉이 그대로 Double DQN에도 연결됩니다.
Maximization Bias
논문에는 과대평가된 행동을 선택하는 경우에 대해 조금 더 자세하게 설명하고 있습니다. (아무래도 문제를 해결한 부분에서 가장 중요한 개념이어서 그런 것 같습니다.) 기존의 Q-Learning 및 DQN 알고리즘에서는 다음 상태의 추정된 Q값들 중 최대값을 사용하여 현재 Q값을 업데이트합니다. 하지만 이 과정에서 추정값에 오차나 노이즈가 포함되어 있을 경우, 최대값을 선택하는 연산 자체가 실제보다 큰 값을 선택하게 되는 경향이 있다고 합니다. 이러한 현상을 Maximization Bias, 즉 행동 가치의 과대평가 문제라고 합니다. 결과적으로 에이전트는 실제로는 최적이 아닌 행동을, Q값이 높게 추정되었다는 이유만으로 선택하게 되며, 이로 인해 학습이 불안정해질 수 있다고 합니다. 과대평가를 하는 bias가 발생하는 원인은 크게 노이즈, 최댓값 선택의 구조, 자기강화 피드백 루프 입니다. Q값은 미래 보상의 기대값을 추정한 것이기 때문에, 특히 학습 초반에는 불확실성이 크다고 합니다. 이 때 노이즈나 오차로 인해 일부 행동의 Q값이 실제보다 높게, 다른 일부는 낮게 추정될 수 있습니다. 또 여러 행동의 Q값 중 가장 큰 값을 선택할 때, 운 좋게 우연히 과대평가된 값이 선택될 가능성이 높습니다. 실제로는 가치가 동일한 여러 행동이 있어도, 추정값이 높은 행동이 선택되면서 bias가 발생합니다. 이로 인해 평균적으로 추정된 최대 Q값은 실제보다 항상 높은(양의 편향) 값을 갖게 된다고 합니다. 마지막으로 한 번 과대평가된 Q값을 가진 행동이 선택되면, 그 행동이 더 자주 선택됩니다. 그리고 반복적인 선택을 통해 얻은 경험으로 Q값이 계속 업데이트되면서, 과대평가가 유지되거나 더 강화될 수 있습니다. 이러한 과정은 비최적 행동을 고집하게 되는 악순환을 초래합니다.
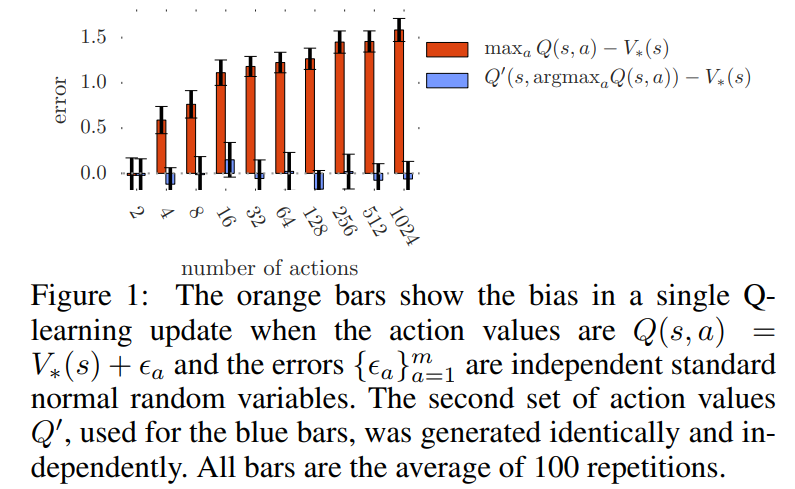
저자는 이런 현상이 일반적임을 강조했는데요, Q-learning이 겪는 과대평가 현상이 단순한 예외적인 경우가 아니라, 이론적으로도 일반적으로 발생할 수밖에 없는 현상임을 수학적으로 보여주고 있습니다. 상태 S에서 모든 행동의 실제 최적 Q값이 동일하다고 가정하더라도, 즉 Q∗(s,a)=V∗(s)인 상황에서도 과대평가가 발생한다는 것입니다. 이때 에이전트가 사용하는 Q값 추정치들이 평균적으로는 정확하더라도, 즉 ∑a(Qt(s,a)−V∗(s))=0으로 unbiased 이더라도, 추정치들 간에 분산이 존재하게 되면 단순히 최대값을 선택하는 연산만으로도 실제보다 높은 Q값이 선택될 가능성이 생긴다고 합니다. 수학적으로는 이때 Q값의 분산이 C이고, 행동의 개수가 m일 때, 최대 Q값은 최소한 V∗(s) + sqrt(C/m−1) 이상이 될 수 있다는 lower bound를 증명하였으며, 이는 tight bound, 즉 가능한 가장 강한 불평등식이라고 합니다. 이 결과는 Q-learning이 실제 강화학습 환경에서 얼마나 쉽게 과대평가에 빠질 수 있는지를 보여주는 이론적 증거가 되며, 반면 같은 조건에서 Double Q-learning은 과대평가 하한이 0이 될 수 있어 보다 안정적인 추정이 가능함을 함께 보여준다고 합니다. 또한 이 이론은 추정 오차들이 서로 독립이라는 가정을 필요로 하지 않기 때문에 실제 다양한 상황에서 적용될 수 있으며, 논문에서는 행동 수가 많아질수록 이론상 하한은 작아지지만, 실제 실험에서는 오히려 행동 수가 많아질수록 과대평가가 커지는 경향이 나타났음을 아래와 같은 figure로 보입니다.
더 나아가서 저자들은 Q-learning의 overestimation 문제를 실험을 통해 시각화해서 보여주었습니다. 아래 figure의 중간 열에 있는 그래프는 한 상태에서 가능한 10개의 행동 각각에 대한 Q값 추정치(녹색 선)와, 이들 중 최대값(검정색 점선)을 함께 보여주고 있습니다. 이 실험에서는 실제로는 모든 행동의 Q값이 동일하도록 설정되어 있으나, 각 행동에 대해 사용된 샘플 상태들이 다르기 때문에 추정된 Q값은 서로 차이를 보이게 되었다고 합니다. 이러한 세팅으로 인해 추정된 Q값들 간의 불균형이 발생하고, 이로 인해 상태별 최대 Q값은 실제 참값보다 높은 경우가 많아지게 됩니다. 왼쪽 열의 보라색 선은 모든 행동의 실제 Q값(V*)을 나타내며, 검정 점선보다 낮은 위치에 있는 경우가 많습니다. 오른쪽 열에서는 검정 점선(추정 최대값)과 보라색 선(실제값)의 차이를 주황색 선으로 나타냈는데, 이 주황색 선이 대부분 양수인 것을 확인할 수 있어 Q-learning이 체계적인 과대평가를 하고 있다는 것을 확인할 수 있습니다.
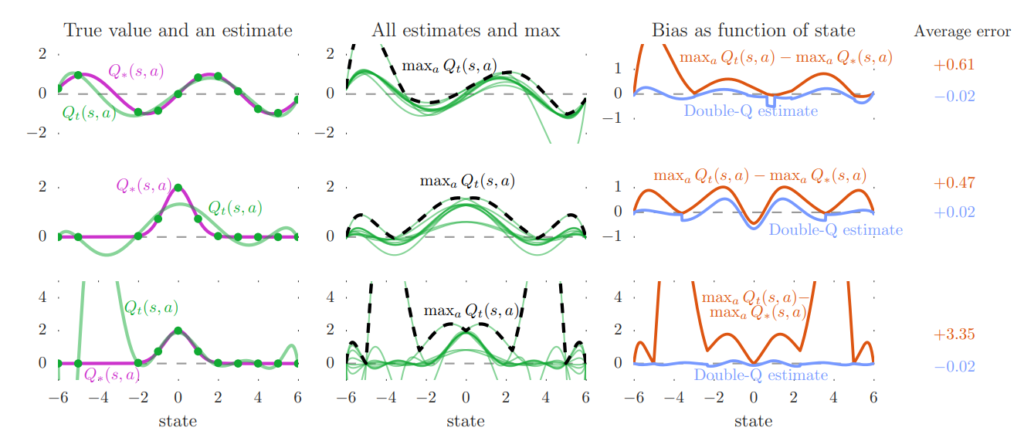
반면, 같은 실험 조건에서 Double Q-learning으로부터 얻은 추정치들은 파란색 선으로 표시되며, 대부분 참값에 훨씬 가까운 위치에 있음을 확인할 수 있습니다. 이 결과는 Double Q-learning이 Q-learning에 비해 과대평가를 명확히 줄여줄 수 있다는 것을 입증하는 사례라고 합니다. 위 figure의 각 행은 동일한 실험 조건에서 일부 요소만 변경한 경우들입니다. 예를 들어, 상단 행과 중간 행의 차이는 실제 Q값 함수 자체이며, 이를 통해 과대평가는 특정 참값 함수의 구조 때문이 아니라 보편적인 문제임을 보여줍니다. 중간 행과 하단 행의 차이는 함수 근사기의 유연성 차이인데, 하단의 경우 함수가 더욱 유연해져 더 많은 상태를 학습할 수 있음에도 불구하고,unseen states에 대해 오히려 추정 오차가 더 커지면서 과대평가도 심화되는 현상이 관찰됩니다. 이는 Q-learning의 구조적 한계를 드러낸다고 합니다.
또한, 저자의 실험은 이전의 연구와는 달리 통계적 근거 없이 deterministic하게 수행되었고, 오류가 불가피한 근사기를 쓴 것도 아니기 때문에, 과대평가는 보다 일반적인 현상이라는 점을 강조하고 있다고 합니다. 특히 이 실험은 특정 상태에서 실제 Q값을 알고 있다는 가정하에 수행되었는데도, 부트스트래핑을 통해 과대평가가 전파되면서 전체 정책 학습의 질을 저하시킨다는 점을 명확히 보여주고 있습니다. 이처럼 Q-learning의 과대평가는 단순히 값이 커지는 문제가 아니라, 상태 간 상대적 가치의 왜곡을 일으켜 결국 policy의 품질을 저해하는 부정적인 효과를 가진다는 점에서 매우 치명적이라고 합니다.
Double DQN
Double DQN은 기존 Q-learning에서 발생하는 과대평가 문제를 해결하기 위해 제안된 Double Q-learning의 핵심 아이디어를 그대로 DQN 구조에 최소한의 변경만을 가해 적용한 알고리즘이라고 합니다. Double Q-learning과 마찬가지로 이 알고리즘의 주요 전략은 TD 타겟의 최대값 계산 과정에서 action selection과 action evaluation를 분리하는 것입니다.
Double Q-learning에서는 두 개의 Q함수를 따로 사용하여 행동을 선택할 때는 하나의 Q함수를, 평가할 때는 다른 Q함수를 사용합니다. 이로 인해 최대값을 취하는 과정에서 특정 행동이 우연히 높게 추정되더라도, 그것이 그대로 업데이트에 반영되지 않도록 편향을 완화할 수 있습니다. 그러나 DQN 구조에서는 하나의 Q-network와 하나의 target network만을 사용하므로, 새로운 네트워크를 추가하지 않고 이 분리를 구현할 방법이 필요했다고 합니다.
Double DQN에서는 이를 다음과 같이 해결합니다. greedy policy를 결정하는 데에는 메인 네트워크로 온라인 네트워크를 사용하고, 그 선택된 행동의 가치를 평가하는 데에는 타겟 네트워크를 사용합니다. 이처럼 기존 DQN의 구조를 유지하면서도 두 개의 Q함수를 구성할 수 있는 구조적 기반을 활용했다고 합니다. 결과적으로 계산 복잡도를 올리지 않고 효과적으로 문제를 해결했다고 합니다. Double DQN의 Y는 아래와 같습니다.
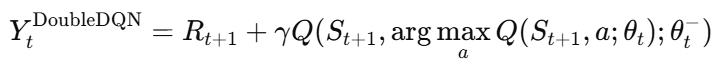
즉, 다음 상태 S_{t+1}에서의 최적의 액션a^*는 온라인 네트워크 theta_t로 선택하고, 그 행동의 Q값은 타겟 네트워크 theta^-_t로 평가하는 구조입니다.
Empirical Results
Double DQN은 DQN의 과대평가 문제를 해결하고자 제안된 방법으로, 논문에서는 이를 value accuracy, policy quality측면에서 평가하였다고 합니다. 실험은 DQN과 동일하게 Atari 2600 게임에서 진행되었으며, 화면 픽셀만을 입력으로 받아 각 게임을 독립적으로 학습하는 구조로 도메인에 특화된 튜닝 없이 진행했다고 하니다. 네트워크는 기존 DQN 구조를 그대로 사용하며 CNN을 통해 마지막 4개의 프레임을 입력받아 Q값을 출력하도록 설계되었습니다. 학습은 각 게임에 대해 단일 GPU로 2억 프레임(약 1주일) 동안 수행되었다고 합니다.
실험 결과 Double DQN의 효과는 Atari 게임에서 명확하게 나타났다고 합니다. 아래 figure에 따르면, DQN은 훈련 중 일관되게, 때로는 매우 심하게 현재 탐욕 정책의 가치를 과대평가하는 경향을 보였으며, 이는 학습 곡선이 실제 최종 정책의 할인 누적 보상보다 훨씬 높은 위치에 위치한 것을 통해 확인할 수 있다고 합니다. DQN의 가치 추정 곡선(주황색 곡선)은 항상 참값(주황색 직선)보다 위에 있으며, 이는 과대평가가 존재함을 시사합니다. 반면 Double DQN의 가치 추정 곡선(파란색)은 참값(파란색 직선)에 더 가깝게 수렴하며, 실제로는 참값 자체도 더 높게 나타나 policy quality 역시 더 우수함을 보여줍니다.
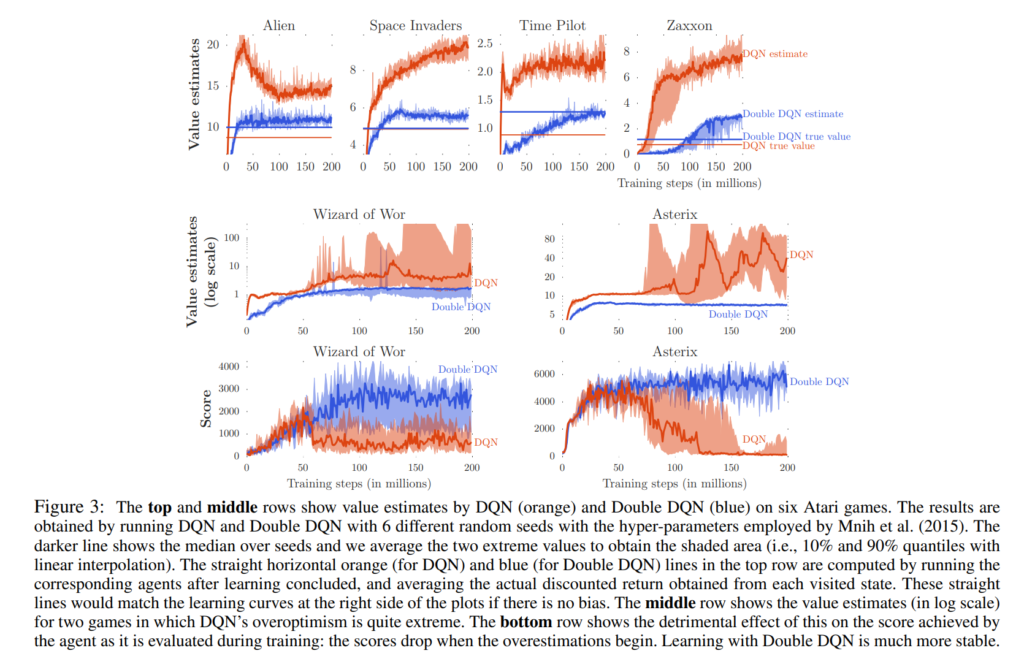
특히 Asterix와 Wizard of Wor 게임에서는 DQN의 가치 추정이 매우 불안정하게 요동쳤으며, 이는 지표가 로그 스케일로 표시되어 있음에도 불구하고 값이 급격히 증가하는 것으로 나타났습니다. 하지만 이때 실제 점수는 오히려 감소하여, 과대평가가 정책 품질을 악화시키는 주된 원인임이 분명히 드러났다고 합니다. 이러한 현상은 단순히 off-policy 학습의 불안정성 때문이라고 보기 어렵고, Q-learning의 구조적overoptimism이 핵심 원인이라는 사실을 실험적으로 보여줍니다. 결정적으로, 이러한 과대평가는 Asterix, Wizard of Wor처럼 극단적인 예외에만 국한된 것이 아니라, 총 49개 게임 전체에서 관측되었으며, 정도만 다를 뿐 모든 게임에서 나타났다고 합니다. Double DQN은 이와 같은 전반적인 과대평가 경향을 효과적으로 완화하여, 더 정확한 가치 추정과 더 나은 정책을 동시에 제공한다는 점에서 DQN 대비 명확한 개선을 보인다고 결론지을 수 있었다고 합니다.
