[NIPS2016] Unifying Count-Based Exploration and Intrinsic Motivation

안녕하세요 박성준 연구원입니다. 오늘은 강화학습 리뷰를 가져왔습니다. 해당 논문은 알파고로 유명한 구글 딥마인드 팀에서 작성한 논문으로 기존 강화학습에 딥러닝을 연계한 DQN 모델에 관한 내용입니다.

리뷰에 앞서 본 논문을 이해하기 위해 알아야한 내용들을 소개하겠습니다.

Reinforcement Learning

강화학습은 에이전드(Agent)가 환경(Environment)와 상호작용하며, 보상을 최대화하는 방향으로 행동을 학습하는 방식을 말합니다. 쉽게 얘기하면, 모델이 주어진 환경 속 최선의 행동을 할 수 있도록 학습하는 것입니다. 이 과정에서 새로운 행동을 시도해 보상을 확인해 보는 것을 Exploration(탐험)이라고 하고 해본 행동 중에 가장 보상이 높은 행동을 하는 것을 Exploitation(이용)이라고 합니다. 당연하게도 Exploration과 Exploitation 사이의 밸런스를 잘 잡는 것이 강화학습에서 중요한 과제 중에 하나 입니다. 이 논문은 Count-based exploration을 다루게 되는데 count-based exploration은 state(상태) 별 방문 횟수를 기반으로 방문이 적은 상태에 보상을 더 크게 함으로 exploration을 유도하는 방법을 말합니다.

위 그림은 tabular 환경을 설명하는 표입니다. tabular 환경은 table 기반 방법론으로 모든 state(상태)와 action(행동) 사이에 테이블 값을 기록하고 행동에 따른 보상을 계산하는 방법입니다. 이와 같은 방식으로 표를 통해 기대 보상을 계산하여 에이전트의 행동을 결정하는 알고리즘이 Q-Learning입니다. Q학습과 같은 count-based exploration은 tabular 환경에서는 잘 작동하지만, tabular 환경이 아니라면 잘 작동할 것이라 기대하기 어렵습니다. 실제 환경에서는 굉장히 많은 상태와 행동이 존재하기에tabular 환경으로 표현하기 힘들고, 때문에 count-based exploration을 현실에 적용하는 것에는 어려움이 있습니다.

Deep Q Network(DQN)

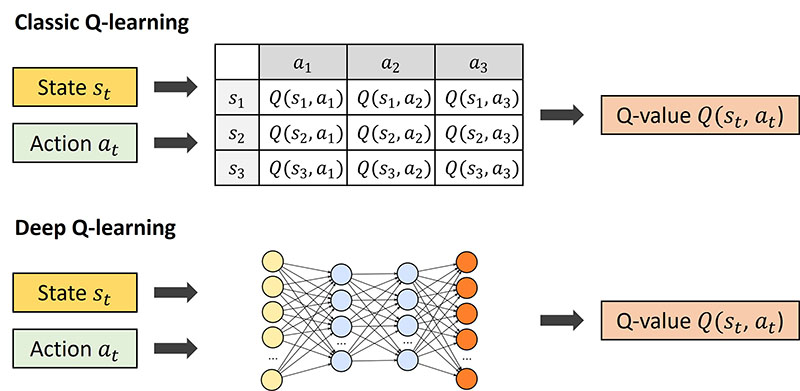
Deep Q Network는 2013년 구글 딥마인드에서 공개한 모델로 Q학습에 딥러닝을 결합한 모델입니다. Q학습에서 사용하는 보상 방식은 Q(s,a)로 나타내며, state s에서 action a 를 했을 때 받을 것으로 예상되는 총 보상에 해당합니다. 모델이 Q값이 높은 행동을 택할 수 있도록 가이드해주는 것을 의미합니다. Q값은 DQN 이전에는 tabular 환경에서 표로 휴리스틱하게 지정하여 사용하고 있었습니다.

DQN은 복잡한 게임 혹은 실제 환경에서는 모든 상태를 표로 저장할 수 없었고, 딥러닝 모델(CNN)을 통해 Q값을 예측하는 모델입니다. 자세하게 내용을 다루지는 않겠지만, 일반적으로 다음과 같은 단계를 통해 동작합니다.

1. 게임 화면을 입력받아 CNN을 통해 모든 행동에 따른 Q(s,a)값 예측
2. \epsilon -greedy 전략을 통해 대부분은 Q값이 높은 행동, 가끔 랜덤한 행동을 통해 Exploration 수행
3. Action 수행 및 보상 획득
4. 경험(행동과 행동에 따른 보상)을 저장해두고 나중에 무작위로 꺼내 학습

이러한 DQN은 기존 Q학습에서 더 발전되어 굉장히 많은 상태와 행동이 존재하는 환경에서도 강화학습의 최적화가 가능하게 만들었습니다. 이번에 제가 리뷰하는 논문은 DQN을 제안한 구글 딥마인트 팀에서 DQN을 개선하는 알고리즘을 제안하는 연구입니다.

DQN의 자세한 내용은 김영규 연구원의 리뷰를 참고바랍니다.

본 연구 이전의 DQN은 count-based 방식을 사용했지만, 저자는 DQN에 pseudo-counts와 density modeling을 적용하는 것을 통해 count-based 방식을 보완하는 방법을 제안합니다. 실제로 Atari 게임(옛날 콘솔 게임)에서 효과가 있었음을 보이며 저자가 제안하는 방법의 강력함을 보입니다. 특히, ‘몬테주마의 복수’라는 강화학습으로 해결하기 어렵다고 악명높은 게임에서도 어느정도 대응할 수 있는 방법임을 보이고 있습니다.

이어서 논문에 대한 내용입니다. 강화학습의 특성상 논문에 알고리즘에 대한 수식이 많이 등장하는데 설명에 있어 필수적인 수식을 제외하고는 많이 생략할 생각입니다(어렵기도하고 말로하면 쉬운설명을 수식으로 어렵게(?) 풀어놓은 부분들이 많네요). 중간에 이해가 안되는 부분이 있으시다면 댓글로 남겨주시면 답변하겠습니다.

Introduction

강화학습에서의 Exploration은 Agent가 Reward(보상) 함수와 Transition(전이) 함수에 대한 불확실성을 줄이기 위한 행동입니다. MDP(Markov Decision Process)에서는 Agent가 환경에 대한 규칙(보상 혹은 전이)를 모르는 상대로 학습을 시작합니다. 어떤 state(상태) x에서 action(행동) a을 했을 때의 얻는 reward(보상) 혹은 다음 상태는 확률적으로 결정되는 데, 이를 직접 알 수 없기에 exploration을 통해 이 state를 얼마나 많이 경험했는 지(방문횟수N(x,a))가 count-based exploration에서 중요한 지표로 활용됩니다.

예를 들어 아래의 수식은 기존의 count-based exploration을 나타낸 수식입니다.

\hat{R}(x,a)은 exploitation 기반의 경험한 보상이고, \hat{P}는 그 transition 확률입니다. 여기서 마지막 항인 \beta N(x,a)^{-1/2}가 exploration에 대한 보너스로 방문 횟수가 적다면 보상을 크게 설정하여 가보지 않은 곳을 가보도록 유도합니다. 이 방식은 이론적으로는 정확도와 최적화가 보장된다고 합니다. 하지만, real world에서는 이러한 방식이 잘 작동되지 않는다고합니다. 그 이유는 상태 공간이 너무 크기 때문에 한번만 보고 두번은 다시 볼 수 없는 상태들이 너무 많고, 그러한 상태들의 방문횟수(N(x,a))는 1이하 이기에 exploration에 대한 보너스가 의미가 없어집니다. 이러한 단점의 해결을 위해 기존 방법론들은 \epsilon -greedy 전략을 통하여 이 문제를 해결하려고 했습니다. \epsilon -greedy 전략은 단순하게 랜덤하게 한번씩 행동들을 섞는 전략입니다.

저자는 이러한 단순한 알고리즘을 통해 문제를 해결하려고 시도하는 것은 바람직하지 못하기에 \epsilon -greedy 전략이 아닌 다른 방식을 통해 기존 count-based exploration이 아닌 다른 방법을 필요성을 강조합니다. 저자의 Intrinsic Motivation에 관심을 갖게 되는데 Intrinsic Motivation은 외부 보상이 없어도 surprise를 찾게 만드는 방식으로 사람이 호기심에 의해 학습하는 것을 모방한 방법입니다. Agent도 사람과 마찬가지로 surprise를 보상으로 받게 함으로 학습하는 것을 말합니다.

위의 수식은 Intrinsic Motivation의 학습을 나타내는 것으로 e는 error를 의미합니다. 즉, 어떠한 행동으로 인해 error가 줄었다면 무언가를 학습했으므로 보상을 주는 방식을 말합니다. 이와 같은 방식은 Markov property가 없어도 사용 가능하기에 count-based exploration보다 더 범용적으로 사용할 수 있습니다. 하지만, 직관적으로는 이해할 수 있는 Intrinsic Motivation 알고리즘은 당시에는 논리적으로 설명되지 않아(이론의 부족) 크게 활용되지 않고 있었습니다.

Information Gain(정보 취득)은 exploration을 통해 uncertainty가 줄었는 지를 수치화하는 방법입니다. 저자는 이러한 Information Gain을 통해서 Intrinsic Motivation과 Count-based exploration을 수학적으로 설명하는 것으로 Intrinsic Motivation을 도입하고자 했고, 그 과정에서 pseudo-count 개념을 사용해 통합적인 프레임워크를 제안합니다. pseudo-count 생성 방식으로는 state 자체의 등장 빈도를 기반으로 density(밀도)를 측정하는 density model을 사용하여 이 밀도를 pseudo-count로 생성합니다. 즉 논문의 내용을 정리하면, density model을 통해 pseudo-count를 생성하고, 기존 count-based exploration과 intrinsic motivation을 결합하여 사용합니다.

수식들을 설명하기 이전에 notation들을 정리하겠습니다. X는 countable(셀 수 있는) state(이후로는 상태라고 하겠습니다)의 집합입니다. x_{1:n}은 길이가 n인 상태 시퀀스입니다. p_n(x):=p(x|x_{1:n})에서 p는 과거 시퀀스를 기반으로 다음 상태가 x일 확률을 예측하는 density model입니다. 즉, p_n(x)는 다음 상태가 x일 예측 확률입니다. 말이 좀 어려운데 만약에 이전 상태들이 [2, 4, 6, 8] 일때 p_4(10)은 앞선 4번의 상태 시퀀스를 토대로 다음 상태가 10일 확률을 말하고 조건부 확률이라 이해하시면 될 것 같습니다. Empirical Distribution \mu_n는 상태 x가 시퀀스 x_{1:n}에서 얼마나 자주 등장했는지를 나타내는 비율입니다. N_n(x)는 Empirical Count Function 즉, 몇번 상태에 방문했는 지를 나타냅니다.

Pseudo-count

드디어 논문에서 제안하는 pseudo-count를 계산하는 방법에 대한 설명입니다. 조금 복잡해보일 수 있지만, 잘 뜯어보면 생각보다 그리 어렵지는 않습니다.

기본 아이디어 자체는 Introduction에서 설명한게 전부고, 굉장히 심플합니다. 기존 tabular 환경에서의 강화학습은 방문횟수 N_n(x)를 기반으로 적을수록 보상을 크게 주지만, 실제 환경에서는 방문이 0인 환경이 대부분이기 때문에 효과적이지 못합니다. 따라서 저자는 방문횟수와 같은 개념의 실제 환경에서도 사용할 수 있는 일반화된 개념의 필요성을 느끼고 pseudo-count를 제안합니다.

앞서 설명드린 것과 같이 pseudo-count는 밀도 모델 p(x|x_{1:n}을 통해 생성됩니다.

p'는 Recording Probability입니다. 데이터 압축 이론에서의 Recording과 비슷한 뜻(압축률?정도로 생각하시면 됩니다)으로 상태 x를 한번 보고난 후에 모델이 얼마나 상태 x를 익숙하게 인식했는지를 계산하는 것과 연결됩니다. 추가로 \hat{N_n}(x)는 구하려는 pseudo-count입니다.

위 수식 둘을 연립방정식으로 묶으면 아래의 수식과 같이 표현됩니다.

위 수식이 최종적으로 밀도 모델로부터 pseudo-count를 계산하는 공식입니다. 위 수식은 밀도 모델의 두 확률 차이로부터 pseudo-count를 계산하고 x 상태를 보기 전과 보고난 후의 값의 차이에 따라 얼마나 많이 증가하는 지에 따라 pseudo-count가 결정되고, 새로움이 클수록(얻는 정보가 많을수록) pseudo-count는 작고, 새로움이 작으면(이미 익숙한 상태)일수록 pseudo-count가 큽니다. 이는 상태 x가 얼마나 모델에게 새로웠는 지를 판단합니다.

저자는 결과적으로 모델의 분포(p_n(x))가 경험적 분포(\mu_n(x))와 같다면 pseudo-count는 실제 count(방문횟수)와 같기 때문에 count의 일반화된 버전이라고 설명합니다. 저자는 실제로 FREEWAY 게임에서의 예시를 통해 pseudo-count의 효과성을 입증합니다.

저자는 다섯가지 조건이 충족된다면 pseudo-count가 count와 같이 사용될 수 있다고 말합니다.

• pseudo-count는 0에 가까운 값으로 시작해야 한다.
• 신뢰할 수 있는 크기를 가져야 한다.
• 상태의 등장 빈도 순서를 잘 반영해야 한다.
• 실제 count와 선형관계에 있어야 한다.
• non-stationarity(비정상성)에도 강건해야 한다.

Figure 1.은 실제 FREEWAY게임에서의 예시입니다. 길건너친구들 게임과 같은 게임으로 지나다니는 차를 피해 무단횡단해야하는 게임입니다. 저자는 기대했던 5가지의 조건이 모두 충족되었으며 실제 count의 비율과 pseudo-count의 비율이 비슷함을 설명하며 exploration 전략으로 이 pseudo-count가 효과적임을 설명하고 있습니다.

Intrinsic Motivation

이번에는 Intrinsic Motivation입니다. pseudo-count가 방문횟수의 일반화된 개념이라면 Intrinsic Motivation은 얼마나 새로운 지를 측정하는 기준인 Information Gain에 연관된 개념입니다. 확률 모델 p 하나가 아니라 여러 개의 밀도 모델 M에서 고른다고 가정했을때 확률의 수식은 다음과 같습니다.

w_n(p)는 n시점에서 모델 p에 대한 posterior 확률입니다. 이 posterior 확률은 다음과 같이 표현됩니다.

posterior는 새로운 데이터에 대한 확률로 베이지안과 같은 개념이기에 자세한 설명은 생략하겠습니다.

Information Gain(IG)의 정의는 위의 수식과 같습니다. 방문 후에 모델의 불확실성을 얼마나 줄었는가를 나타내는 KL-발산입니다. 이때, IG를 계산하는 것은 쉽지 않기에 저자는 실제 학습 때에는 IG를 Prediction Gain(PG)로 대신해서 계산한다고 합니다.

PG는 밀도 모델의 확률에 로그를 취하는 것으로 예측 확률이 얼마나 개선되었는 지를 계산합니다. 즉, 여기서 pseudo-count와 수식적으로 연결됩니다(p_n의 활용). 위 방법은 pseudo-count를 활용하여 간단한 수식으로 구현이 가능하면서도 최적성을 보장한다고 합니다.

그 후에 저자는 PG에 대해서 이론적으로 정리하며 내용을 정리합니다. 핵심은 PG는 learning-positive 상황에서는 항상 0이상이고 PG가 커질수록 pseudo-count는 작아지는 반비례 관계라는 점입니다. 즉, pseudo-count 기반 보너스와 같은 방식으로 동작합니다.

마지막으로 저자는 Asymptotic Analysis(점근적 분석)를 통해 pseudo-count가 실제 visit count와 비슷하게 수렴한다는 것을 수학적으로 증명하게 되는데, 해당 부분에 대한 설명은 생략하도록 하겠습니다.

Experiments

Figure 2는 여러 게임에서의 성능을 비교하며 분석하고 있습니다. 저자의 pseudo-count를 적용한 방법이 가장 좋은 성능을 보이고 있습니다.

특히, Montezuma’s Revenge게임(강화학습에서 Exploration 성능을 평가하기 위해 많이 사용되는 게임으로 난이도가 굉장히 높음)에서는 기존의 방법들이 초기 단게에서 거의 진전이 없는 반면, pseudo-count를 적용하게 되면, 첫번째 방을 넘어 여러 방을 탐험하게 되고 기존 최고 성능을 능가하는 3659점을 달성해 기존 SOTA 방법의 3배에 달하는 점수를 기록했습니다.

다른 게임에서도 월등한 성능을 보였으며, pseudo-count가 exploration을 촉진하고 일반화가 가능함을 보여줍니다.

논문에서는 DQN의 실험결과가 잘 보이지 않아 구글 딥마인드가 논문 공개당시 공개한 pseudo-count를 적용한 DQN의 게임 영상 링크를 첨부하며 리뷰 마치겠습니다.

감사합니다.