[PMLR 2020]Being Bayesian, Even Just a Bit, Fixes Overconfidence in ReLU Networks

여러분은 논문의 제목을 보면서 어떤 내용일 것으로 추측되시나요?

네, 제목 그대로 bayesian 구조를 일반적인 딥러닝 네트워크에 도입함으로써, 딥러닝 네트워크에서 학습 데이터에 대한 overfitting 등으로 발생하는 overconfidence 문제를 해결할 수 있다는 것이 본 논문의 내용입니다.

흥미로운 내용이죠? 지금부터 아래의 목차를 기반으로 논문을 소개해보겠습니다.

• ## 목차 ##
• [용어정리] Overconfidence는 무엇인가
• [용어정리] 베이지안과 ReLU 네트워크의 차이
• [본문: intro] 논문 소개 (컨셉 소개)
• [본문: method] 베이지안 구조를 딥러닝 네트워크에 도입하는 법 (본 논문의 주요 방법론)
• [본문: prove] 실험 결과 (제안 방법론의 우수성 및 효과 검증)
• [본문: Conclusion] 마무리

---

Overconfidence 무엇인가

Overconfidence라는 단어는 꽤 많이 접해보셨을 것 같은데요, 그럼에도 다시 한번 리마인드 해보겠습니다. 단어를 이해할 수 있는 가장 좋은 방법은, 그 용법이나 예시를 확인하는 것이므로 딥러닝에서 Overconfidence가 왜 문제 시 되는지 알아봅시다.

딥러닝은 수많은 파라미터로 입력 신호를 통해 적절한 출력 신호를 생성하는 방법입니다. 특히 딥러닝 기반 이미지 분류 문제를 생각해보면, 일반적으로 입력 이미지가 어떠한 카테고리에 속할 확률이 출력 값이 됩니다. 즉, 예측에 대한 신뢰도(확률)을 함께 생성 출력 신호에 포함하게 되는 것이죠.

그런데, 딥러닝 모델이 학습 데이터에 너무 과적합하게 될 경우, 일반화 성능이 저하되어 학습데이터에 포함되지 않은 분포에 대한 예측에 오류가 발생하게 됩니다. Overconfidence는 이러한 오차로 인한 현상 중 하나이며, 옳지 않은 예측에 대한 신뢰도가 높아지는 현상입니다. 이 현상의 원인은 다양하나, 그 중 하나는 딥러닝 기반 이미지 분류 문제의 이상적인 출력값이 one-hot vector 이므로, one-hot vector 분포와 같이 예측을 특정 클래스에 높은 확률로 예측하게 되는 것 입니다.

정리하면 Overconfidence는 모델이 예측에 대한 신뢰도를 잘못 예측하게 되는 현상입니다. 상업 서비스에서 활용되는 모델이 예측에서 신뢰도를 잘못 반영하게 되면 틀린 예측에 대해서도 서비스의 출력값에 활용되는 등의 문제가 발생하게 되어, 이를 해결하는 것은 딥러닝 학습에 중요한 문제 중 하나 입니다.

베이지안과 ReLU 네트워크의 차이

MacKay(1992a)에 따르면 bayesian neurall networks는 학습되지 않은 데이터에 대해 낮은 확신도를 갖으며, 위에 설명된 Overconfidence 현상에 강인합니다. 본 논문은 이러한 현상을 이용해 딥러닝의 Overconfidence를 해결하는데요, 논문의 이해를 위해 두 구조의 차이를 간단하게 이해해봅시다.

먼저 우리에게 친숙한 ReLU 네트워크는 일반적인 딥러닝입니다. 딥러닝의 학습과정은 대수의 법칙에 따라 학습 데이터(표본 집단)가 실제 데이터(모집단)의 분포를 반영하며, 학습데이터를 통해 결정 경계를 학습하면 실제 데이터를 분류하기 위한 최적의 결정 경계를 생성할 수 있다는 가정을 내포합니다. 딥러닝이 학습 데이터셋의 크기에 의존적이라는 근거도 이와 같습니다.

반면 베이지안 네트워크는 prior이라는 결정 경계를 학습 데이터의 관찰 전부터 가정하고 있으며 학습 데이터 관찰에 따라, 관찰의 발생 가능성을 높이도록 posterior를 업데이트 하는 학습 과정을 반복합니다. 따라서 베이지안 네트워크는 학습데이터가 적더라도, prior에 의존한 모델을 설계할 수 있으며, 관찰한 학습 데이터에 대한 의존성이 ReLU 네트워크에 비해 약합니다.

[Intro] 논문 소개

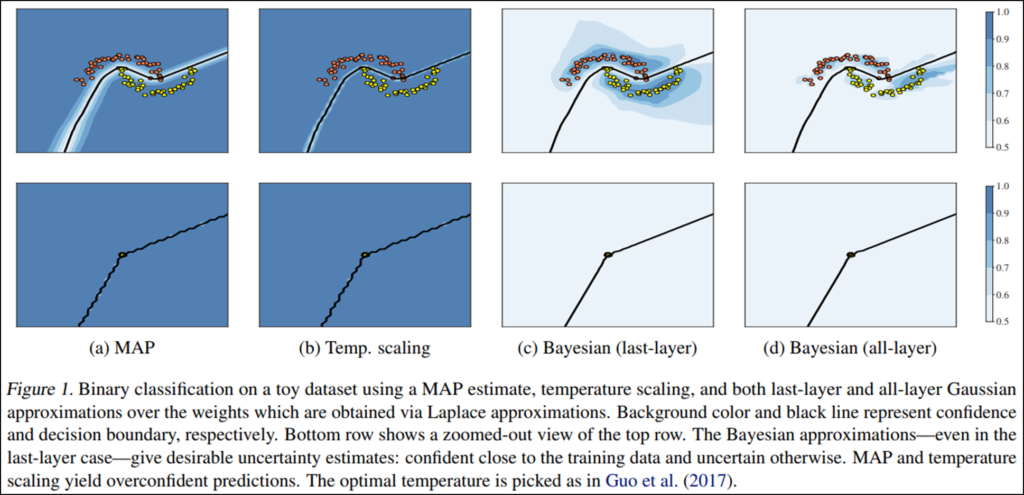
논문은 베이지안 구조의 일부 차용을 통해 ReLU 네트워크의 Overconfidence 현상을 완화할 수 있음을 보이고 있습니다. 위의 Figure1은 논문의 컨셉을 잘 이해할 수 있는 대표 실험 결과입니다. 이미지들의 1행의 붉고 노란 점에 대한 이진 분류 문제의 학습 결과로, 결정 경계(검정 라인)와 예측의 확신도를 나타낸 것이며, 오른쪽의 범주에서 알 수 있듯이 파란색에 가까울 수록 높은 확신도로 예측하였습니다. ReLU 네트워크인 (a), (b)의 경우 학습 데이터의 외부 분포에 대해서도 높은 확신도로 예측을 수행함을 알 수 있으며, MacKay(1992a)가 증명하였듯이 베이지안 구조인 (d)는 학습하지 않은 분포에 대해 낮은 확신도로 예측을 수행했습니다. Figure 1에서 주목할 점은 (c)인데요, ReLU의 마지막 레이어에만 bayesian을 적용하더라도, (d)와 같은 효과를 낼 수 있다는 점이 잘 보이는 논문의 메인 이미지 입니다.

[Method] 베이지안 구조를 딥러닝 네트워크에 도입하는 법

본 논문이 베이지안 구조를 도입하는 법은 아주 간단합니다. L-layer network를 L-1 Layers와 bayesian linear classifier로 구분하는 것으로, 즉, 마지막 레이어만을 베이지안 네트워크로 바꾸는 방법입니다. 수식적 증명은 아래와 같습니다.

1. (문제 정의를 위한 사전지식: 문제 설정) 기존 딥러닝 방법의 문제점

(Hein et al, 2019)에서도 논의 된 기존 딥러닝 방법의 문제는 입력 데이터가 분포를 벗어날수록 confidence가 높아진다는 것입니다. 즉, 불확실한 데이터에 대해 확신도 높은 예측을 하는 Overconfidence 현상이 발생하는것이 문제입니다. 이 문제를 수식적으로 나타내면 다음과 같습니다.

2. (문제 정의를 위한 사전지식: 기존 해결책) 베이지안 딥러닝의 해결책

앞선 연구(Hein et al, 2019)에 따르면, 기존 딥러닝의 학습 분포 외 데이터에 대한 예측의 문제점은 분포에서 크게 벗어날수록(δ→∞) 예측에 대한 확신도(softmax 출력값)이 높아진다는 점이였습니다.

베이지안 러닝의 경우 (δ→∞)에 따른 예측 확률이 상수로 수렴하기에 딥러닝에서 발생하는 overconfidence 현상이 발생하지 않아 해결책이 될 수 있었으며, 이에 대한 수식적 표현은 아래와 같습니다.

3. (논문이 제시하는 해결책) Last layer modification의 효과

베이지안 러닝이 Overconfidence 문제 등에 강인한 것은 이미 MacKay(1992a)에서 연구되었습니다. 따라서 last layer에 베이지안 구조를 적용하여, 완전 베이지안 네트워크의 이점을 갖을 수 있음을 증명한 해당 파트가 본 논문의 메인입니다. 즉, last layer에만 베이지안 네트워크를 적용하더라도 δ가 발산할 경우에 그에 따른 예측 확률이 상수로 수렴함을 증명할 수 있다면, 딥러닝의 단순한 구조변경(just being “a bit” bayesian)으로도 overconfidence를 해결할 수 있음을 보인 것 입니다. 본 논문은 이를 수식적으로 증명하였으며, 수식은 아래와 같습니다.

[Prove] 실험 결과

위에서는 제안하는 방법이 overconfidence를 해결할 수 있음을 이론적으로 증명하였습니다. 이어서 논문은 Toy datasets에 대해 제안 방법이 효과적임을 증명하였습니다. 실험은 LeNet(for MNIST)과 ResNet-18(CIFAR-10, SVHN, CIFAR-100)에 대해 진행되었습니다. 일반적인 딥러닝 학습 방법인 MAP와 그 결과를 Temporal scaling한 것, 제안 방법론(last-layer Laplace approximation, 이하 LLLA) 및 완전 베이지안 방법, 총 4가지 방법론의 결과가 리포팅 되었습니다. 실험은 Binary Classificaiton 실험과 Multi-class OOD detection 두 가지로 진행되었으며 그 결과는 아래와 같습니다.

*Temporal scaling: 은 overconfidence를 해결하기 위한 방법 중 하나로, 스케일 팩터(Τ)로 예측된 출력값을 나누어 과도한 확신도를 정규화 하는 방법임
*또한 베이지안 방법으로는 라플라시안 근사를 통한 DLA, KFLA 등의 방법론이 사용되었습니다.

# Binary Classification 실험: classify it! in-distribution(1) or out-of-distribution(0)

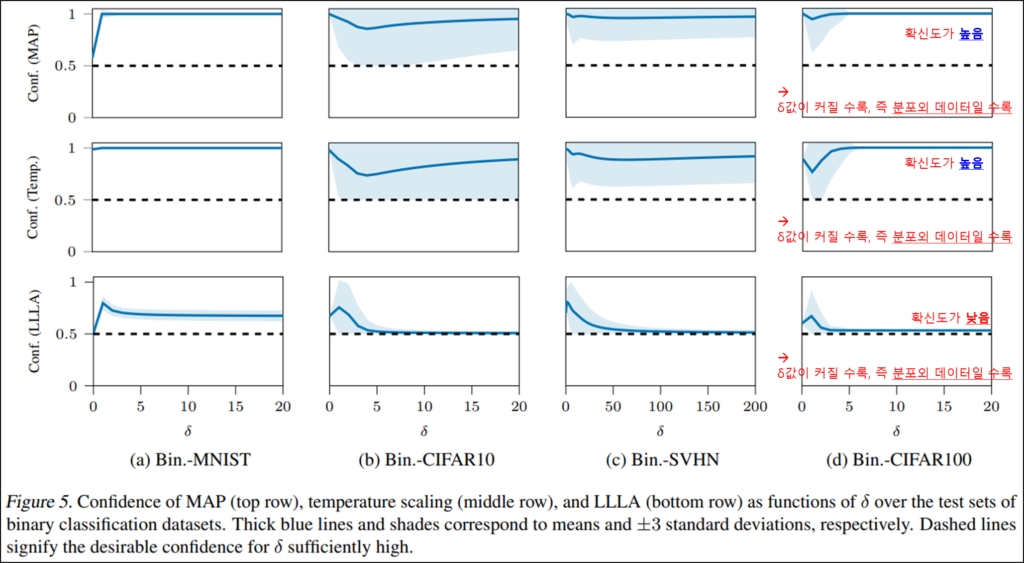
위의 Figure5는 데이터 분포 파라미터 δ에 따른 confidence(예측 확신도) 그래프로 제안 방법론인 LLLA를 적용하였을 때 분포 외 데이터에 대해 높은 확신도로 예측하는 Overconfidence현상이 개선되었음을 확인할 수 있습니다.

# Multi-class Classification: classify it! in-distribution or out-of-distribution(SVHN, LSUN, CIFAR10 or noise)

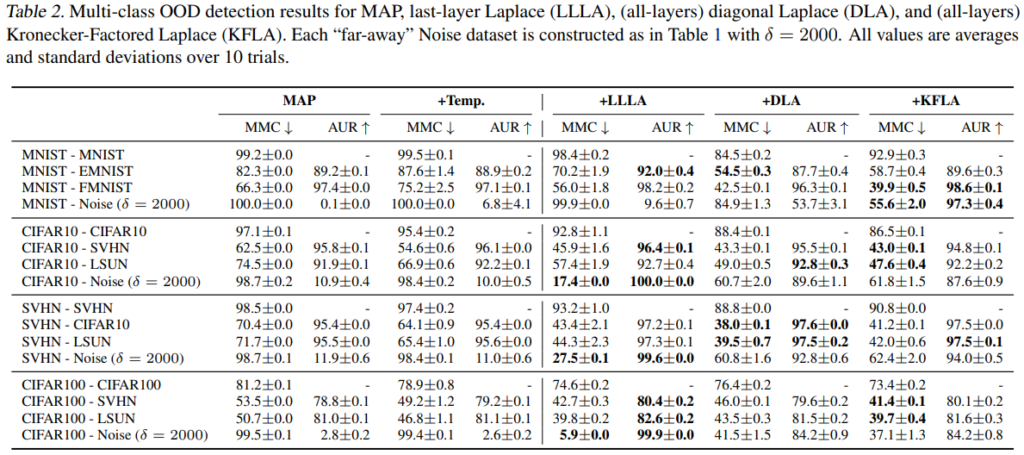
Table2는 기존 딥러닝 학습법인 MAP에서 Overconfidence를 해결하기 위해 단순 스케일링 방법인 Temporal scaling(Temp.), 제안 방법인 LLLA, 비교를 위한 기존 베이지안 근사 방법론인 DLA, KFLA를 적용하여 리포팅 하였다. meanmaximum-confidence (MMC)와 Out-of-distribution 성능인 area-under-ROC-curve(AUR)를 리포팅 하였으며, MAP의 경우 noise 데이터에 대해서도 높은 confidence로 예측하였지만(MMC score 참조) 제안 방법과 베이지안 방법은 이를 효과적을 개선하였음을 알 수 있습니다. 또한 제안 방법은 last layer만을 modification 하여, 기존 딥러닝의 성능에 대한 손실 없이 다른 베이지안 근사 방법(DLA, KFLA)보다 높은 정확도로 out-of-distribution detection을 수행하였음을 확인할 수 있습니다.

즉, 제안 방법은 last layer에만 “a bit”(약간의) 변형을 통해 기존 딥러닝 성능에 대한 손실없이 overconfidence를 해결할 수 있음을 Table2의 실험으로 확인할 수 있습니다.

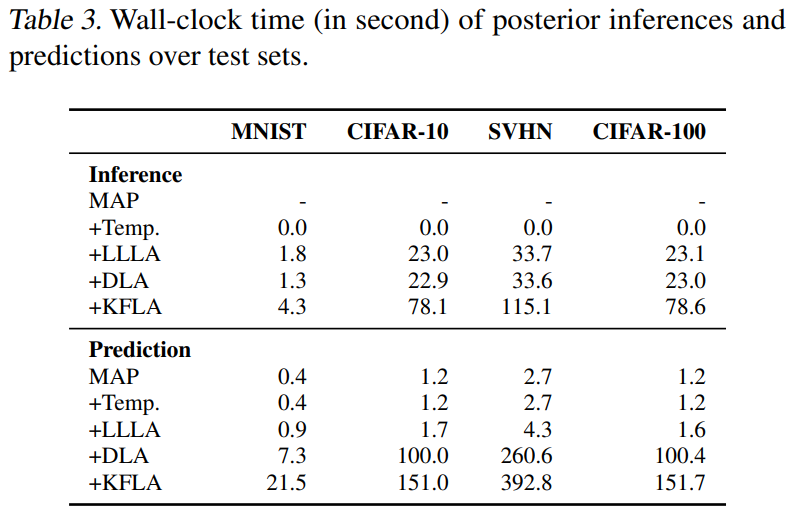
기존 베이지안 근사 기법 대비 장점은 성능 뿐만이 아닙니다. 제안 방법은 베이지안 기법을 약간만 도입하였기에, 기존 방법보다 inference time이 짧다는 장점이 있으며, Table3의 추론 시간 비교를 통해 이를 확인할 수 있습니다.

마무리

본 논문은 “being a bit bayesian”을 통해 베이지안의 이점과 기존 딥러닝의 이점을 모두 갖을 수 있음을 이론적, 실험적으로 증명하였습니다. 특히 기존 딥러닝의 Overconfidence 문제를 비교적 손쉽고 분석 가능한 접근법으로 해결할 수 있음을 보이는 논문이였습니다. 감사합니다.

---

베이지안 딥러닝은 예측의 안전성 개선에 효과적입니다. 하지만 연산량이 많다는 단점을 지니기에, 이를 근사하거나 일부만 도입하여 베이지안 딥러닝과 동일한 효과를 보일 수 있음을 증명하는 연구들이 많이 수행되고 있으며, 본 논문도 그러한 논문 중 하나입니다. 흥미로운 논문이네요, 그럼 리뷰를 마치겠습니다.