오늘 리뷰할 논문은 이미지 분류 모델의 예측 성능 개선에 중점을 맞추어 모델 불확실성을 산출하고, 이를 통해 성능을 개선하는 능동 학습 (Active Learning)에 관련된 논문입니다. 특히 본 논문은 기존 베이지안 능동 학습 (Bayesian Active Learning) 방법을 개선하는데 초점을 맞추었습니다. 기존 방법들은 모델 불확실성 산출에 집중했지, 실질적 성능 개선은 고려하지 못했기 때문입니다. 그럼 리뷰 시작하겠습니다.
배경 지식: 베이지안 능동 학습
베이지안 학습(Bayesian Learning)은 모델 파라미터를 고정된 값으로 간주하는 빈도주의적 접근과 달리, 파라미터를 확률 분포로 표현하여 파라미터의 불확실성을 정량화할 수 있도록 설계됩니다. 베이지안 능동 학습(Bayesian Active Learning)은 이러한 파라미터 불확실성을 기반으로 데이터의 가치를 평가하여 학습에 사용할 데이터를 선택하는 방법론입니다. 이는 일반적인 딥러닝 연구에서 모델링하는 빈도주의적 모델이 예측의 불확실성을 수치화 하는 방식 (모델 출력의 분포나 대조 학습(Contrastive Learning) 등의 추가 기법으로 통해 간접적으로 산출)과는 다른 방식입니다.
빈도주의적 딥러닝 모델은 P(y|x) (x는 입력 데이터, y는 라벨)과 같은 출력 분포를 기반으로 예측의 신뢰도를 수치화합니다. 이는 베이지안 능동 학습에 비해 활발하게 연구되며 예측 성능 개선에 효과적이지만, 불확실성의 정의가 방법론마다 상이하여 직관성과 해석 가능성이 떨어집니다. 반면, 베이지안 학습은 P(θ|x, y) (θ는 모델 파라미터)와 같은 체계적이고 직관적인 방식으로 불확실성을 모델링합니다. 이는 파라미터의 불확실성을 명확히 정의할 수 있다는 장점이 있으나, 베이지안 능동 학습의 근본적인 한계는 예측 성능 향상보다 파라미터 정보량의 최대화에 초점을 둔다는 점입니다.
논문에서는 비모수적 모델(nonparametric model)을 사례로 들며 이러한 한계를 설명합니다. 비모수적 모델에서는 학습 데이터가 증가함에 따라 모델 파라미터의 개수가 유동적으로 변합니다. 베이지안 능동 학습을 이 모델에 적용하면 데이터 증가로 파라미터 불확실성은 줄어들 수 있으나, 선택된 데이터가 실제로 예측 성능 개선에 기여하지 않을 가능성이 있습니다. 이는 전체 데이터 분포와는 관련성이 낮거나 모호한 데이터를 고가치로 평가할 위험성을 초래합니다.
정리하면, 베이지안 능동 학습은 파라미터의 정보량 증가를 목표로 직관적인 데이터 가치를 산출할 수 있지만, 모델의 불확실성 정도 개선이 예측 성능 향상과 직접적으로 연결되지 않는다는 한계가 존재합니다. 이러한 점은 본 논문의 새로운 접근법을 논의하는 중요한 배경이 됩니다.
소개:
본 논문은 기존 베이지안 능동 학습의 한계를 극복하고자 기대 예측 정보 이득(Expected Predictive Information Gain, EPIG)이라는 새로운 접근법을 제안합니다. EPIG는 기존 방법(BALD)[1]이 초점을 맞췄던 모델 파라미터의 정보 이득이 아닌, 예측 공간에서의 정보 이득을 최대화하여 데이터의 가치를 평가합니다. 이를 통해 데이터 선택 과정이 단순히 파라미터 불확실성을 줄이는 데 그치지 않고, 모델의 예측 성능 개선과 직접적으로 연결될 수 있도록 설계되었습니다.
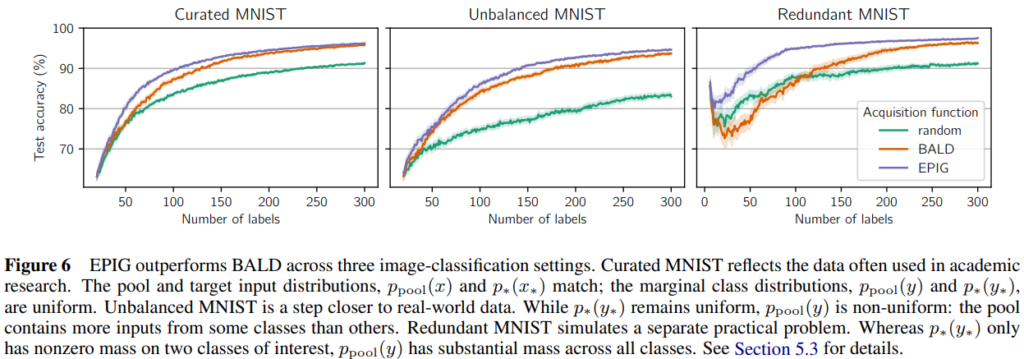
모델의 예측 성능 개선에 직접적인 연관성을 높임으로서 기존 베이지안 능동 학습(BALD)[1]에 비해 안정적인 성능 개선을 보였음을 아래의 Figure 6으로 확인할 수 있습니다. 특히 가장 우측의 Redundant MNIST는 제안 방법(EPIG)의 안전성을 보여줍니다. Redundant MNIST는 기존 MNIST에 가우시안 노이즈나 랜덤 패턴 등을 추가하여 복잡성을 높인 데이터셋 입니다. 해당 데이터셋에서 BALD는 단순 정보량 개선을 목표로 해, 노이즈 데이터를 고가치 데이터로 평가하여 Random 성능 대비 성능이 오히려 하락하는 모습을 보였습니다. 그러나 EPIG는 이러한 데이터셋 환경에서도 성능 개선을 보이며 기존 베이지안 능동 학습의 한계를 극복했음을 보였습니다.
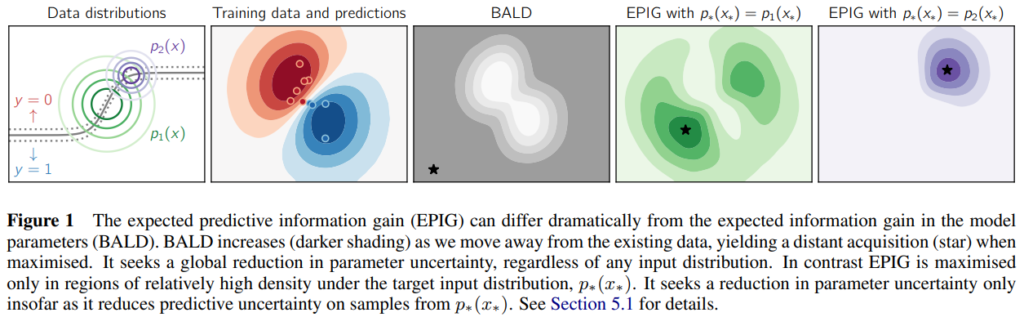
다음은 BALD와 EPIG를 활용하여 고가치 데이터를 선별시 선별되는 데이터의 차이를 시각화한 것입니다. 가운데의 BALD의 경우 학습하지 않은 데이터와 거리가 먼 데이터들을 동일하게 회색영역으로 표시하여 결론적으로 outlier에 해당하는 검은 점을 고가치 데이터로 선별했습니다. 그러나 제안 방법의 경우 입력 분포에 따라 예측에 도움이 될 수 있는 경계선 근처의 데이터(녹색, 보라색 별)를 고가치 데이터로 선별했음을 확인할 수 있습니다.
방법론:
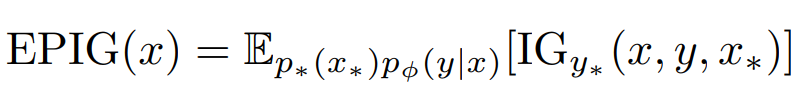
본 논문에서는 데이터 x로 부터 개선할 수 있는 정확한 IG(정보량)를 모델링하기 위해 정답 분포(target distribution)인 p∗를 EPIG 수식에 도입합니다. 위 수식은 EPIG는 데이터 (x, y)를 학습함으로써 랜덤하게 선택된 데이터 포인트 x∗에서 모델이 얼마나 더 나은 예측을 할 수 있는지를 수치화 합니다. 특히, 새로운 데이터(p∗(x∗))와 예측(pϕ(y∣x))의 발생 확률을 고려한 평균을 정보량을 계산(E_p∗(x∗)pϕ(y∣x))하게 됩니다.
이때 정답 분포를 사용한다는 것은 존재하는 모든 데이터를 알고있다는 명제를 내포합니다. 즉, 불가능하죠. 베이지안 방법론들은 정답 분포를 모사하기 위해 샘플링 기법을 활용하며 본 논문에서는 대표적인 샘플링 기법인 몬테카를로 (Monte Carlo) 방식을 활용합니다. 샘플링 기법은 샘플을 추가하여 최종적인 분포를 추정하는 방법입니다. EPIG 또한 수집한 데이터(pool)을 이용하여 target input distribution(p∗(x∗))를 추정합니다. 특히 web-scaled data에 대해 노이즈는 많은 반면, label은 신경써야 할 요소가 적어 비교적 정확함을 이용해 아래의 수식2을 가정할 수 있으며, 이를 활용해 p∗(x∗)를 수집 데이터를 활용해 주정할 수 있습니다. 추정의 수식은 수식3과 같습니다. p∗(x∗)는 베르누이 법칙에 이해 우항과 같이 전개되며 수식 2를 통해 최종적으로 가장 아래의 수식으로 추정됩니다.
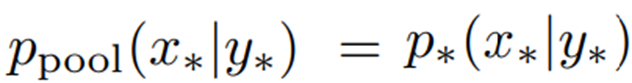
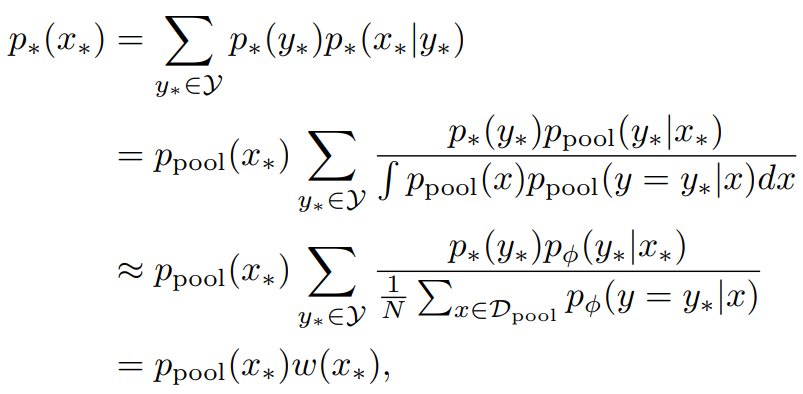
위의 수식 전개는 전체를 파악하시기 어렵더라도 “EPIG 수식이 정답분포를 사용하는데, 실제 능동 학습에서 활용 가능한가?”에 대한 의문으로 수집한 데이터를 활용해 추정한다는 것만 이해하시면 됩니다.
다음은 EPIG를 계산하는 실제 추정 수식의 전개입니다. 정말 EPIG의 정의인 수식1을 전개한것 뿐이라 관심 있으신 분은 아래의 수식4를 훑어보시면 될 것 같습니다. 이때 log의 분수항은 log 항끼리의 차로 바꿀 수 있고, 항 간의 차는 거리로 모델링 할 수 있기 때문에 수식4의 전개를 거쳐 최종적으로 수식5의 KL 거리로 계산할 수 있게 됩니다. 즉, 수식1은 논문이 제안하는 불확실성 산출 방식인 EPIG의 정의고, 수식5는 실질적으로 EPIG를 계산하기 위한 산출식입니다.
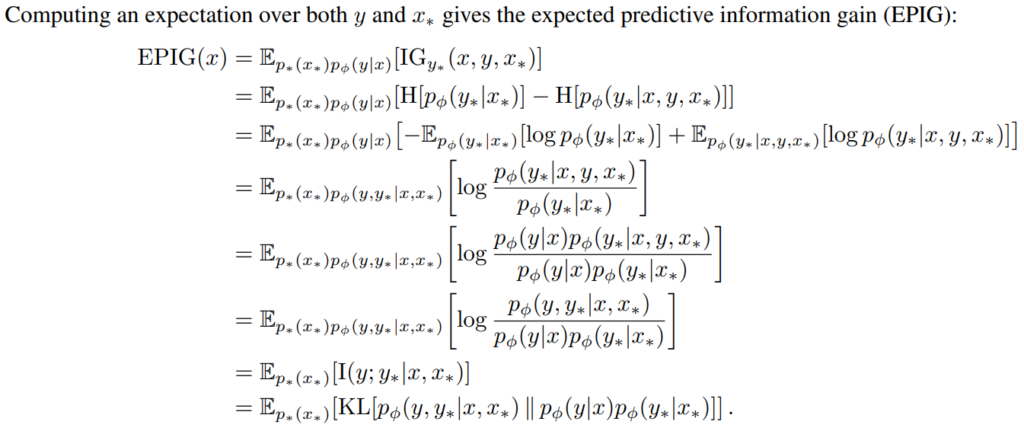
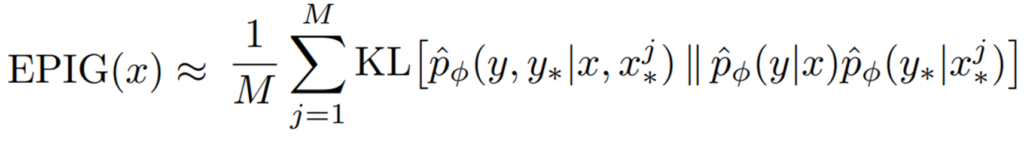
이때 수식5에서 pˆ는 몬테카를로 방식으로 추정한 예측의 분포로 수집된 데이터로 구해집니다. 데이터 x, y를 학습할 때 새로운 데이터 x*, y*의 발생 확률을 수치화하며 결합 분포와 두 분포의 곱의 KL 거리 차이로 구할 수 있습니다.
실험:
실험은 MNIST와 유사하게 적은 특징량을 갖는 쉬운 데이터셋(UCI, MNIST, MNIST 변형)에 대해 진행되었고 BLAD와 Random 성능과 비교가 진행되었습니다. 실험 결과가 시사하는 바는 앞서서 소개한 Figure6의 경향과 유사합니다. 복잡한 데이터셋에서 BALD에서 발생하는 성능 하락 현상이 발생하지 않으며, 전반적으로 BALD 대비 높은 성능 개선을 보입니다.
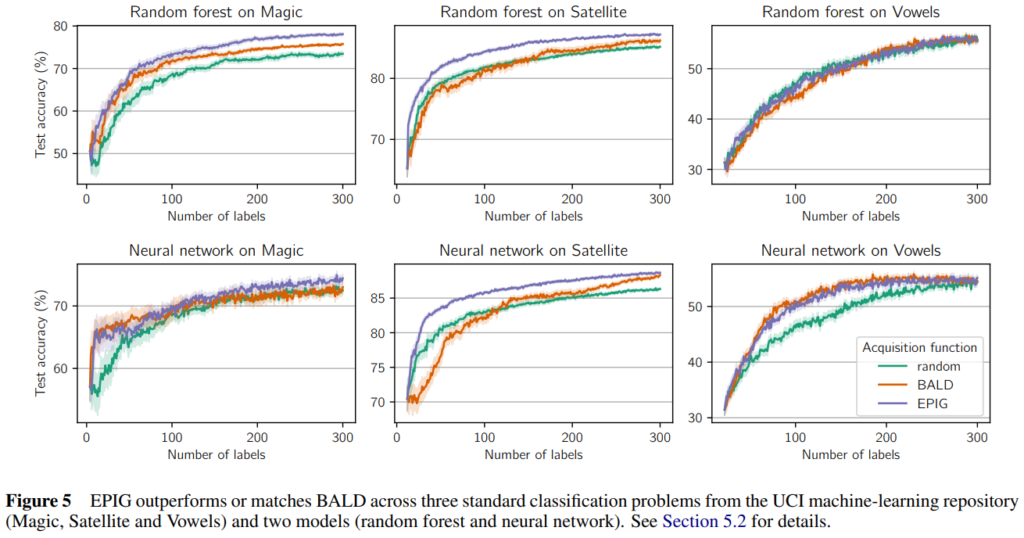
참조:
[1] Houlsby, Huszar, Ghahramani, & Lengyel (2011). ´ Bayesian active learning for classification and preference learning. arXiv.
본 논문은 기존 베이지안 능동 학습 대비 예측 성능 향상을 직접적인 목적으로 하는 불확실성 산출 방식을 제시합니다. BALD에 비해 안정적인 성능 개선을 보이는 것은 긍정적이나, 실험된 데이터가 MNIST 스케일 정도의 매우 쉬운 데이터라는 점이 아쉽습니다. 기존에 소개했던 aleatoric uncentainty, epistemic uncertainty을 제외하고도 Parameter Uncertainty와 Prediction Uncertainty 개념이 본 논문에 소개되었는데요 (기존 BALD는 parameter uncertainty에 타게팅 되었다면 제안 방법은 prediction uncertainty를 고려해 더욱 prediction oriented 된 능동 학습 방법을 설계했습니다) 새롭게 접한 개념인 만큼 이해가 어려웠습니다. 어서 연구가 더 발전되어 해석 가능성 뿐만 아니라 성능적으로도 기존 능동 학습을 압도할 수 있는 방법론이 개발되면 좋겠습니다.
