[ICLR 2021] Free lunch for few-shot learning: Distribution calibration

안녕하세요. 본 논문은 few-shot learning에 관한 논문입니다. 제목에서 알 수 있듯이 데이터 수집 비용 없이 기존의 정보를 활용해 추가 데이터를 생성하여 few-shot learning의 성능을 높인 논문입니다. 특히 few-shot learning의 어려움의 이유로 적은 학습 데이터로 인한 bias를 언급하며 분포를 calibration할 수 있는 데이터를 생성하는 방법론입니다. 자세한 리뷰는 아래를 참고해주세요

---

Few-shot Learning

Few-shot learning 관련 논문을 3번째로 다루기에, 해당 분야에서 사용되는 용어는 친숙하시겠지만 한번 더 다루겠습니다. Few-Shot Learning은 제한된 수의 학습 데이터(특히 클래스당 10개 이하의 샘플)만을 사용해 학습하는 방법에 대한 연구입니다. 따라서 해당 분야는 데이터 부족 상황에서도 모델이 일반화 능력을 갖추도록 만드는 데 중점을 둡니다. Few-Shot Learning은 일반적으로 N-way-K-shot 형태로 정의됩니다.

• N-way: 학습 및 테스트에 사용되는 클래스의 수.
• K-shot: 각 클래스당 제공되는 학습 샘플의 수.
• 예: “5-way-1-shot” 문제는 5개의 클래스를 대상으로, 각 클래스에서 샘플 하나로 학습하고 새로운 샘플을 분류해야 함.

또한 일반적으로 데이터는 다음 두 가지로 구분됩니다:

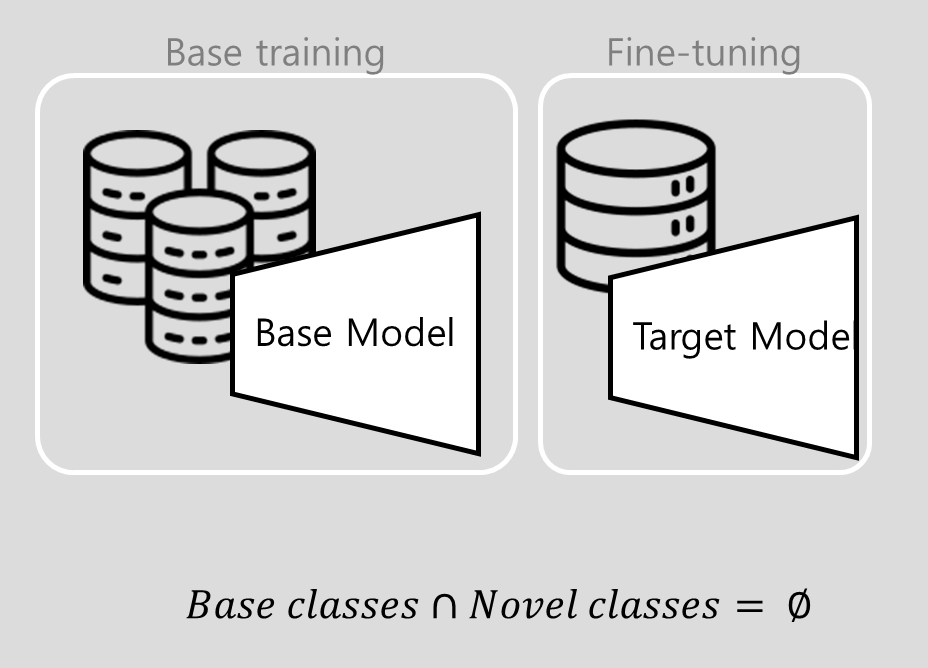
• Base classes: 초기 학습에 사용되는 클래스.
• Novel classes: Target task 수행을 위해 등장하는 새로운 클래스.

이때 base classes와 novel classes 사이에 공통되는 class는 없음이 가정됩니다.

논문 소개

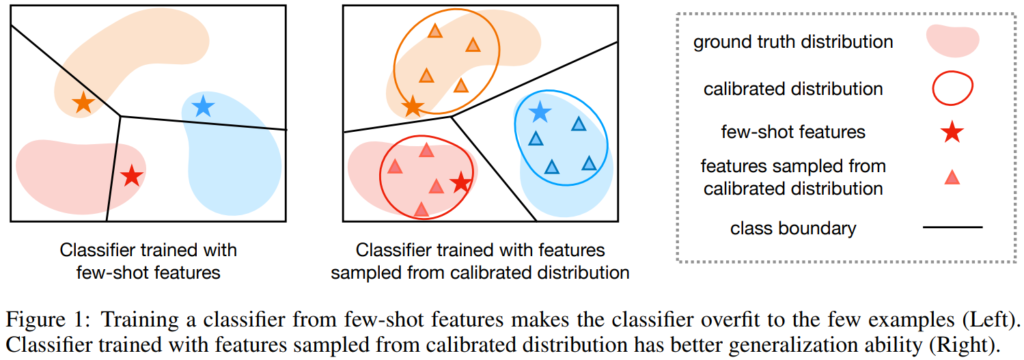
소량의 데이터를 활용해 학습하는 Few-shot Learning은 학습 데이터를 통해 모델을 업데이트 하는 기존의 Supervised Learning 과 동일한 메커니즘을 갖음에도 별개의 분야로 나뉘어졌습니다. 그 이유는 적은 수의 데이터로 학습하는 프로세스에서 발생할 수 있는 어려움 때문입니다. 데이터 편향으로 인한 모델의 일반화 성능 하락은 Few-shot Learning이 해결해야하는 대표적인 문제 중 하나입니다. Figure1은 소량의 데이터가 어떻게 모델의 일반화 성능을 하락시키는지 나타내는 그림인데요, 데이터 선별시에 분포를 고려할 수 없기 때문에 선별된 데이터가 대표성이 낮더라도, 해당 데이터가 클래스를 대표하는 값이 되어 모델의 일반화 성능을 해칠 수 있습니다.

본 연구는 augmentation을 통해 novel class 데이터를 보충하여 최종 target model의 일반화 성능을 개선하는 방법론에 속하며, 해당 연구 방법론 중에서 클래스의 분포를 고려해 bias를 해결하는데 집중한 최초의 방법론입니다. 장점으로는, 학습된 base class의 분포 정보를 활용하여 nover class date를 합성하는 연구로서, 기존에 제안된 상용(off-the-shelf) feature extrector에 쉽게 적용가능하고, feature level의 데이터 augmentation으로 학습 비용이 기존 방법론 대비 낮다는 장점이 있습니다.

방법론

위의 알고리즘에서 확인할 수 있듯이 본 연구의 방법론은 간단합니다. base class를 통해 분포의 평균과 분산을 구하고, 해당 정보를 활용하여 novel class의 분포를 정의한 다음, 정의된 분포에서 feature를 샘플링하여 학습 데이터를 증강하는 것 입니다. 수식을 통해 조금 더 자세하게 알아보겠습니다.

먼저 Algorithm1에 Require로 제시된 base class 의 분포를 구하는 수식은 아래와 같습니다. 본 논문에서 class의 statistic은 가우시안 분포라고 가정합니다. 가우시안 분포는 정규 분포(Normal Distribution)의 가장 대표적인 꼴로, 대칭을 이루는 종모양의 분포이며, 평균(µ)과 분산(Σ)을 정의하면 분포 전체를 특정할 수 있다는 장점으로 데이터의 분포를 모델링하는데 자주 사용됩니다. 따라서 우리는 특정 base class(C_i)에 속하는 base class data의 평균과 분산을 구함으로서 C_i의 분포를 특정할 수 있게되며 그 수식은 아래와 같습니다.

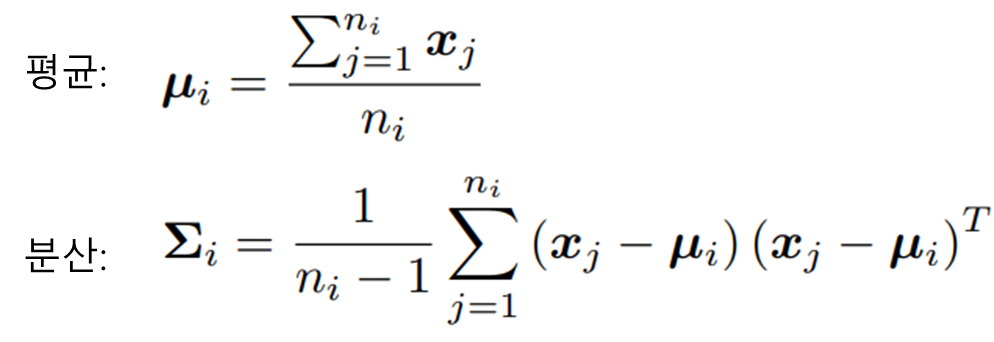
수식은 일반적인 평균/분산을 구하는 수식과 동일하며 feature extrector로 임베딩 된 feature(x)에 대해 평균과 분산을 구하게 됩니다. 여기서 n_i는 클래스 C_i에 속하는 base class의 갯수입니다. 이제 해당 분포를 활용해 novel data의 분포를 정의하게되는데, 이에 앞서 수학적 기법인 Tukey’s Ladder of Powers Transformation을 적용합니다. 이는 분포의 왜도(skewness)를 줄여 데이터를 가우시안 분포에 더욱 가깝게 만들기 위해 주로 사용되는 기법입니다. loss 함수의 적합도 개선을 위해 적용되는 log 스케일 변환을 적용하는 것과 유사한 기법으로 생각하시면 됩니다. Tukey’s Ladder of Powers Transformation의 수식은 아래와 같으며 λ=1일 경우 변환 결과가 원본 함수와 동일합니다. λ=0인 경우 log 변환을 적용하며 λ<1일 경우 분포를 더 평평하게(분산 감소), λ>1일 경우 데이터의 분산을 증가시키도록 동작합니다. 본 논문에서는 λ = 0.5로 설정되었으며, 해당 변환은 base data가 아닌, novel data에 속하는 support set과 query set에 적용됩니다.

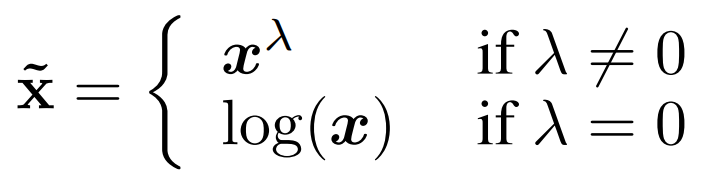
마지막으로 본 연구의 메인이 되는 novel data의 분포 생성 방법입니다. 분포는 feature extretor로 임베딩 된 few-shot novel data와 가장 가까이에 있는 base distribution의 평균을 활용하여 novel data의 분포를 정의되며 수식은 아래와 같으며, 본 논문에서는 k = 2로 설정되었습니다.

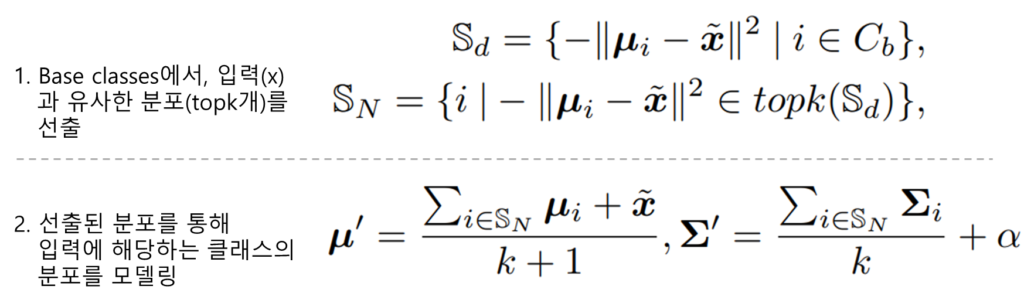
마지막으로 Sampling은 간단합니다. 정의된 분포에서 랜덤 샘플링하여 클래스 y에 속하는 데이터 x를 생성합니다. 데이터의 생성을 위해서는 다변량 정규 분포에서 랜덤 샘플링하는 np.random.multivariate_normal 모듈이 사용되었으며, 클래스 당 750개의 데이터를 샘플링 하였습니다. 이렇게 증강된 데이터를 활용하여 (classification task의 경우) Target task를 수행하는 분류기를 학습하게 됩니다.(라벨이 존재하므로 일반적인 cross-entropy 적용 가능)

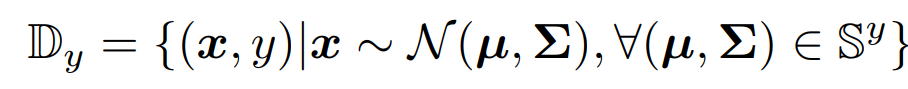
실험

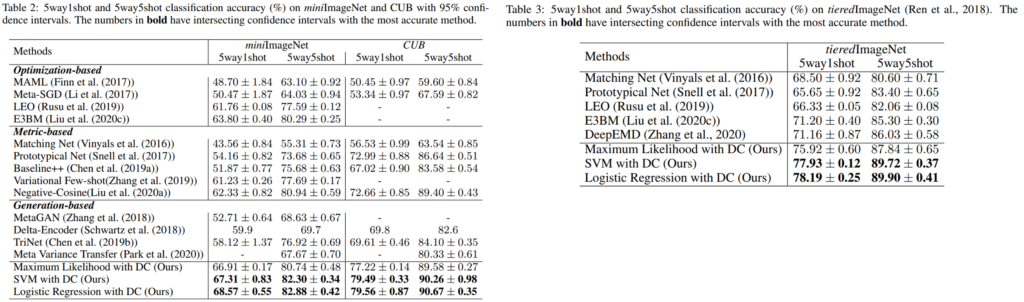
가장 먼저 제공된 정량적 평가는 SOTA와의 비교실험(Table2-3)입니다. 비교적 쉬운 데이터인 miniImageNet와 CUB과 이에 비해 real-world에 가까운 데이터셋인 tieredImageNet이 평가에 사용되었으며, 5way 1shot/5way 5shot 세팅에서 제안된 방법론(DC)를 간단한 분류기 (Maximum Likelihood./SVM/Logistic Regreesion)에 적용하였음에도 우수한 성능을 보였음을 확인할 수 있습니다. 또한 해당 방법론은 다른 off-the-shelf 방법론에 쉽게 적용할 수 있어, 분류기 성능 개선시에 더욱 SOTA 대비 높은 성능을 달성 할 수 있습니다.

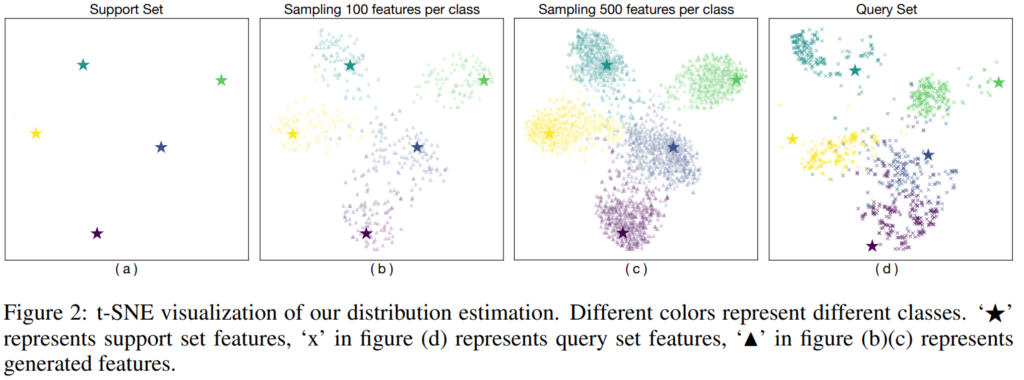
다음은 제안 방법론의 이점을 잘 보여주는 시각적 분석 결과(Figure2)입니다. 위의 (a)가 기본적으로 임베딩된 novel class의 feature(support set)이며, (b)와 (c)는 제안 방법론(DC)로 생성한 feature를 같이 표현공간에 나타냈습니다. 이때 (b)는 클래스당 100개의 샘플을 (c)는 클래스당 500개의 샘플을 생성했습니다. 가장 우측의 (d)는 실제 전체 query set의 임베딩 결과입니다. (query set과 support set은 모두 novel classes 데이터이며, query set이 support set을 포함함. support set은 Few-shot learning 학습에 사용되는 소량의 데이터이며 query set은 test에 사용됨) 결과에서 확인할 수 있듯이 (b)는 query 분포를 잘 나타내고 있으며, 일부 cover 되지 않은 영역이 있지만, 더 많은 sample을 샘플링 했을 때(c) 이러한 문제가 해결됨을 시각적으로 나타냈습니다.

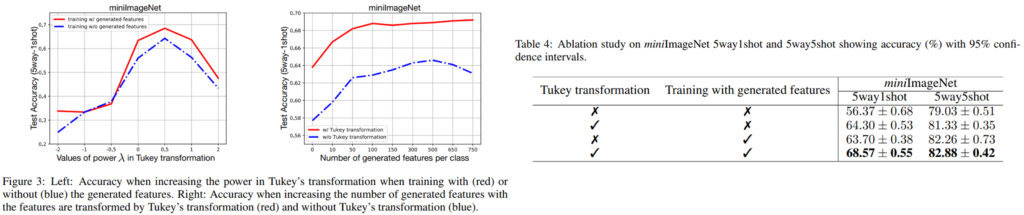
마지막으로 Ablation study입니다. 먼저 사용된 모듈로 novel data의 왜도를 감소하여 학습을 원활하게 하는 Tukey 변환을 적용하는 것과 novel data의 분포를 예측해 feature를 증강하는 기법에 대한 ablation study가 Table4에 제공 되었으며, 두 모듈이 성능개선에 효과적이였음을 보였습니다. 다음으로 각 기법에 사용된 하이퍼파라미터에 대한 효과를 분석했는데, 모든 파라미터에 대해 전반적으로 성능 개선이 있음을 확인할 수 있습니다.

---

이상으로 논문에 대한 리뷰를 마치겠습니다. 편향을 줄이는 것에 집중한 해결책이 궁금하여 읽게 되었는데, 데이터 단위의 분포 보정보다는 클래스 단위의 보정 기법이 많이 사용되는것 같습니다. 제가 실험중인 방법론은 데이터 단위의 모델링에 집중하고 있어 아쉽습니다. 해당 방법론을 실험중인 방법론에 적용 가능한지 테스트 해봐야겠습니다. 다음번엔 조금 최신 논문으로 리뷰하도록 해보겠습다. 감사합니다.