안녕하세요. 이번 주 X-Review에서는 22년도 NeurIPS에 게재된 논문 <Multimodal Contrastive Learning with LIMoE: the Language-Image Mixture of Experts>를 소개해드리겠습니다. 본 논문은 현재 구글 딥마인드로 병합된 구글 브레인에서 나온 연구입니다. 구글에서 수 년 전부터 Mixture of Experts의 구조적 제안을 굉장히 많이 하는 것으로 보이네요. 현재 살펴보고 있는 Video Moment Retrieval 연구에 Mixture of Experts 개념을 도입해보고자 하는데, 여러 논문을 읽던 중 멀티모달에 MoE를 적용한 논문이 있어 리뷰하게 되었습니다.

기존에 V-MoE라는 방법론을 제안한 논문이 있는데, 해당 논문은 일반적인 ViT 구조에 포함되어있는 FFN을 MoE 구조로 변경하여 이미지 관련 downstream task들을 수행하였습니다. V-MoE(ViT 구조에 MoE를 적용한 논문)를 기준으로 MoE의 효과부터 설명드리면 일반적으로 기존 ViT보다 연산량을 낮추면서 성능을 유지하거나, 성능을 올리면서 연산량을 유지하는 역할을 수행합니다. 물론 아무렇게나 적용하면 안되고 해당 상황에서 MoE를 적용했을 때 발생하는 문제점을 파악하고 이를 다뤄주는 loss나 구조를 추가해야겠죠. 마치 CLIP을 각자 도메인의 downstream task로 가져와 생기는 문제를 해결함으로써 contribution을 가져가는 상황과 유사하다고 보시면 됩니다. 아무튼 리뷰 시작하겠습니다.
0. Mixture of Experts
본격적인 리뷰를 시작하기 전, Mixture of Experts가 무엇인지부터 말씀드려야겠죠. 원래 Mixture of Experts의 개념 자체는 1991년도에 처음으로 제안되었습니다. 이후 자연어처리 분야에서 대략 10년 전부터 다시 활용되기 시작했고, 이에 대한 효과는 앞서 말씀드린대로 conditional computation로부터 기인합니다. 즉 모델에 포함되어있는 모든 파라미터들이 연산에 관여하는 것이 아니라 특정 조건에 따라 일부 파라미터만 연산에 사용함으로써 연산량을 낮추면서 성능을 올리거나, 성능을 올리며 연산량을 유지할 수 있는 것입니다. 이 때의 비교 대상은 MoE를 적용하지 않은, 일반적으로 dense한 모델이라고 생각하시면 됩니다. Dense는 모든 파라미터가 연산에 가담하는 경우를 의미하고, 자세히는 뒤에서 또 말씀드리겠습니다.
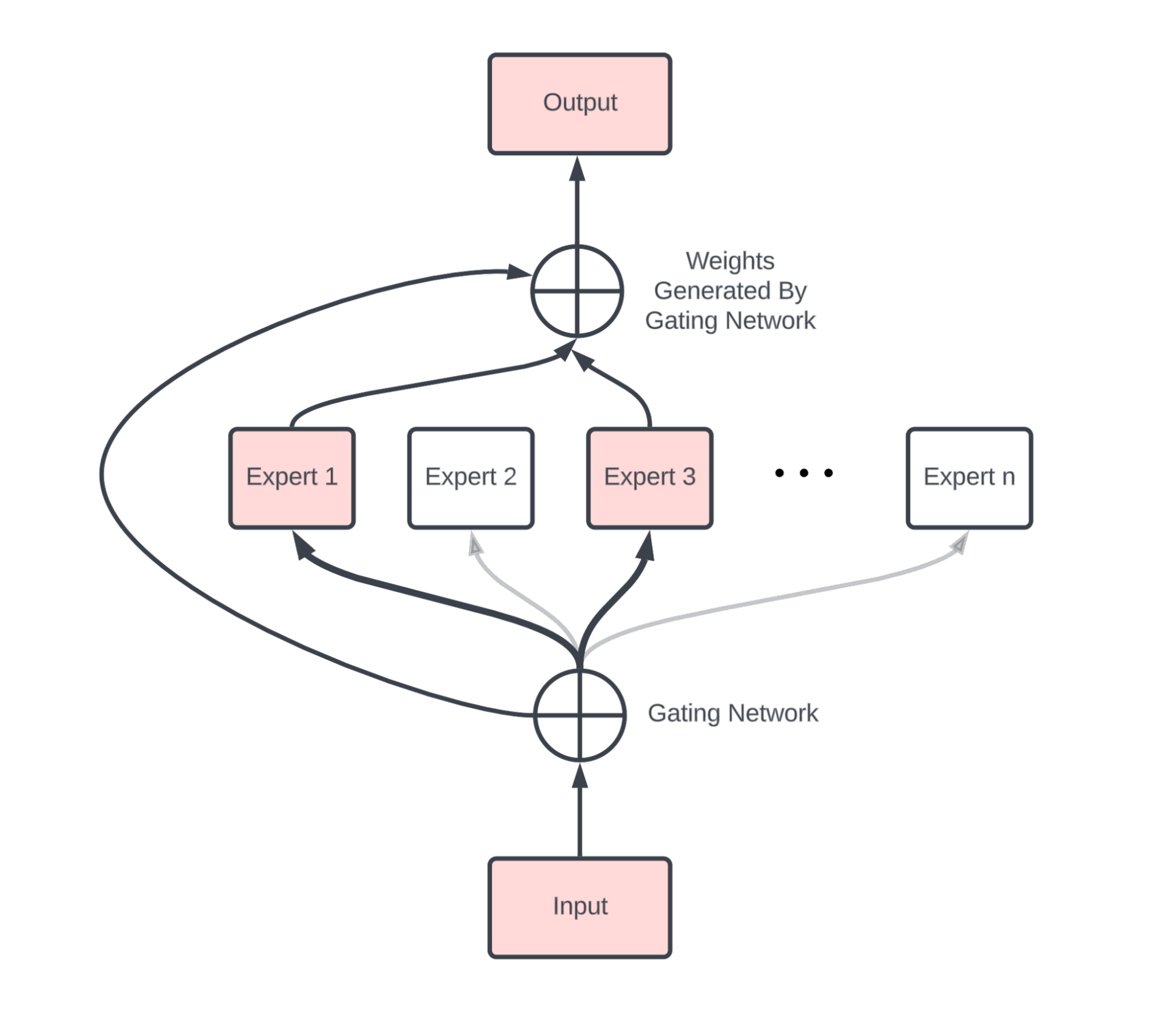
위 그림이 MoE의 일반적인 구조입니다. 우선 입력과 출력 사이 Gating Network와 총 n개의 Expert들이 존재하는 것을 볼 수 있습니다. 네트워크에 입력된 토큰을 Gating network에 입력하여 토큰 당 총 n차원의 벡터를 추출합니다. Gating network는 일반적으로 FC layer + Softmax로 구성되며 방금 입력된 토큰이 총 n개의 expert 중 어디로 가면 되는지 지정해주는 역할을 수행합니다.
위 그림에서는 입력이 1번과 3번 expert로만 향하고 있는데, 보통은 이런 식으로 softmax를 타고 나온 n개의 logit 중 top-1 또는 top-2의 expert로만 forwarding 해주게 됩니다. 선택된 expert로 forwarding하고 softmax로 얻은 각 expert의 weight를 곱해 최종 출력을 만들어내는 것이죠. 이 때 n개의 expert 모두에 forwarding하고 마찬가지로 모든 expert로부터 얻은 출력에 가중합을 곱해 최종 output을 계산해주면 dense하다고 이야기하고, 먼저 설명드린 바와 같이 top-1 또는 top-2의 일부 expert만 사용한다면 sparse mixture of expert라고 이야기합니다.
사실 MoE의 기본적인 목적이 연산량을 낮추며 성능을 유지한다는 점임을 생각해봤을 때 dense한 모델은 효율성 측면에서 오히려 손해입니다. 기존에는 1개였던 FFN을 n개로 늘리고 모두 연산한다면 연산량은 당연히 늘어나겠죠. Dense MoE가 sparse MoE보다 성능은 높지만 연산량 측면에서 손해가 크기 때문에 학계에 등장하는 MoE는 대부분 sparse 모델이라고 보시면 됩니다. 물론 높은 성능이 보장된 Dense MoE의 효율성을 추구하는 연구(Soft MoE)도 일부 존재하는 것으로 보입니다.
MoE가 동일 연산량으로 성능을 올릴 수 있는 이유는, 연산에 관여하진 않지만 모델에 포함되어있는 파라미터 수가 굉장히 많기 때문입니다. MoE 구조를 학습함에 따라 이는 현재 토큰의 특성을 보고 n개의 expert 중 어떤 expert가 담당하면 될 지 파악하게 되는데요, 모델 전체의 파라미터 수는 굉장히 많기 때문에 많은 학습 데이터 샘플에 대해 underfitting 될 확률은 최소화하며, 실제 forwarding에 관여하는 파라미터는 전체 모델 중 일부이기 때문에 기존의 dense한 모델보다 성능을 높이며 연산량을 유지할 수 있는 것입니다.

MoE는 최근 자연어 처리 분야에서 활발히 사용되고 있습니다. 대표적으로 LLM에 많이 적용되고 있는데, MoE는 GPT-4에도 적용되어있기로 유명하고, Mistral AI의 Mixtral 8x7B 모델 또한 MoE 구조로 인해 46.9B개의 파라미터(원래는 8*7로 56B여야 하지만 MoE 특성상 공유하는 레이어가 존재해 이를 제외하고 46.9B)만으로도 위 표와 같이 LLaMA-2-70B에 버금가는 성능을 보여주고 있습니다. 당연히 sparse한 모델이기 때문에 dense한 LLaMA보다 추론 속도가 훨씬 빠르겠죠.
위와 같은 방식으로, 입력 토큰이 일부의 expert만 타고 forwarding 되는 기법을 MoE라 칭하고, 최근 LLM을 넘어 다양한 비전 분야의 downstream task에도 적용되고 있는 추세로 보입니다. 아직 활발하진 않지만, 항상 자연어처리 분야에서 넘어오는 여러 기법 중 하나일 것으로 생각됩니다. 저도 Video Moment Retrieval에서 정의한 몇 가지 문제점들이 있는데, MoE를 적용하여 문제를 해결함과 동시에 효율성도 잡으며 높은 성능을 달성해보고 싶네요.
1. Introduction
자연어 처리 분야에서 연구된 Transformer가 비전 분야로 넘어와 ViT가 연구되었듯, LLM 등 자연어 처리 분야에서 적용되던 MoE를 ViT에 적용한 모델이 V-MoE입니다. V-MoE는 나중에 다시 살펴보는 것으로 하고, 본 논문에서 제안하는 LIMoE (Language-Image MoE)는 멀티모달(이미지, 텍스트) 토큰을 입력받을 수 있는 V-MoE라고 볼 수 있습니다.
MoE는 앞서 설명드린 LLM 모델 Mixtral 8x7B의 사례와 같이 효율적인 모델의 scale-up을 위해 적용되어 왔습니다. 제가 이전의 MLLM 세미나 때도 말씀드렸듯 모델이 가지고 있는 파라미터 개수에 따라 처리할 수 있는 downstream task 범위가 달라졌는데요, 큰 모델들이 더 많은 일을 처리하기에 마냥 좋다고만 볼 수 없는 것이 이 모델을 fine-tuning하거나 재학습할 때 수반되는 cost는 일반적인 규모의 연구실에서는 감당하기 힘든 것이 사실입니다. 그렇기 때문에 많은 파라미터 개수를 유지하며 fine-tuning 등에 소요되는 cost를 최소화하기 위한 여러 기법 중 MoE가 등장하였고 많이들 적용되고 있는 것입니다.
우선 영상 또는 텍스트 중 하나만을 다루는 단일모달 모델에 MoE를 성공적으로 적용한 사례는 당시까지 꽤 많았습니다. 위 단일모달 연구들이 해결해야했던 대표적 문제는 MoE 레이어의 학습 안정성이었습니다. 원인은 정확히 알 수 없지만 Gating 함수를 통해 할당되는 expert가 심하게 한 쪽으로 쏠리는 불균형 문제가 존재하였습니다. 이러한 불균형이 생겨 하나의 전문가가 대부분의 토큰을 처리하게 되면 사실상 MoE 구조를 둘 필요가 없습니다. 연산량 측면에서나 메모리 측면에서 낭비겠죠. 그래서 기존 방법론들은 여러 loss를 두어 입력 토큰이 고르게 할당될 수 있도록 설계해주었습니다.
이러한 와중 LIMoE는 멀티모달, 즉 이미지와 텍스트 입력 토큰을 동시에 다룹니다. LIMoE에서는 먼저 각 모달 간 pair 정보가 주어지기 때문에 기본적인 contrastive learning을 진행합니다. 두 모달의 토큰을 routing해줘야 하는 상황에서 기존 단일모달 방법론에서 발생하고 해결중이던 문제는 여전한지, 또 멀티모달이기 때문에 특별히 고려해줘야 할 점은 없는지 살펴봐야겠죠. 저자는 멀티모달이기에 발생하는 문제를 지적하고 이를 해결하기 위한 entropy based regularisers를 제안합니다. 자세한 내용은 contribution을 정리한 뒤 아래에서 계속 알아보겠습니다.
Contribution
- We propose LIMoE, the first large-scale multimodal mixture of experts models
- We demonstrate in detail how prior approaches to regularising mixture of experts models fall short for multimodal learning, and propose a new entropy-based regularisation scheme to stabilise training
- We show that LIMoE generalises across architecture scales, with relative improvements in zero-shot ImageNet accuracy ranging from 7% to 13% over equivalent dense models. Scaled further, LIMoE-H/14 achieves 84.1% zero-shot ImageNet accuracy, comparable to SOTA contrastive models with per-modality backbones and pre-training.
- Lastly, we present ablations and analysis to understand the model’s behavior and our design decisions
2. Multimodal Mixture of Experts
연구원분들께서 잘 아시는 CLIP을 포함하여 대부분의 멀티모달 learning에서 contrastive learning을 활용합니다. 최근에는 그러한 경향이 많이 줄었지만, 그 당시 기준으로의 이전 멀티모달 방법론들은 이미지 인코더와 텍스트 인코더를 따로 두는 ‘two-tower’ 구조를 가졌습니다. 그러나 저자가 제안하는 LIMoE는 모델의 일반성과 scalability를 높이기 위해 one-tower 구조를 가집니다. 인코더를 따로 두지 않고, 하나의 인코더가 두 모달리티의 토큰을 모두 입력받아 처리한다는 의미입니다.
2.1 Multimodal contrastive learning
n개의 영상과 텍스트 쌍 \{(i_{j}, t_{j})\}_{j=1}^{n}이 주어졌을 때, 모델은 \mathcal{Z} = \{(z_{i_{j}}, z_{t_{j}})\}_{j=1}^{n}을 추출하여 contrastive learning을 수행합니다. 이는 아래 수식 (1)과 같습니다.

CLIP과 동일하게 loss는 image-to-text와 text-to-image 각각 한 term 씩 존재합니다. 일반적인 NCE loss이고, 주어진 쌍에 대한 유사도는 커지고, 배치 내 나머지 샘플과는 유사도가 작아지도록 학습합니다.
2.2 The LIMoE Architecture

LIMoE는 두 모달리티의 토큰을 동시에 입력받아 하나의 Transformer 기반 구조로 처리합니다. 각 모달에 대한 linear layer를 두어 먼저 같은 dimension으로 투영시켜주고, 이를 위해 영상은 먼저 ViT와 동일한 patch로 나뉘게 됩니다. 이후 각 토큰이 모달리티와 관계 없이 입력되는 것이죠. 위 수식 (1)의 contrastive learning에 사용되는 feature z_{i}는 출력을 평균내고 각 모달별 FC Layer에 태워 만들어주는 것입니다.
Sparse MoE backbone
기존 연구들과 동일하게 Transformer 구조의 FFN을 MoE로 대체합니다. 하나의 FFN 층이 gating function과 총 E개의 expert로 변경되는 것입니다. 전체 Transformer 구조로 따지면 여러 개의 MoE 계층이 포함되어 있겠죠. 각각의 토큰 x \in{} \mathbb{R}^{D}는 전체 E개의 experts 중 K개를 선택하여 forward 됩니다. Gating function이 내뱉는 gating weight g(x) =\text{softmax}(W_{g}x) \in{} \mathbb{R}^{E} 중 상위 K개를 선택하는 것이고 이렇게 얻은 feature를 후에 \text{MoE}(x) = \Sigma{}_{e=1}^{K}g(x)_{e} \cdot{} \text{MLP}_{e}(x) 와 같이 weighted sum 하여 출력을 다음 layer로 전달하는 것입니다. 위 식에서 MLP는 각 expert를 의미하겠죠.
2.2.1 Challenges for multimodal MoEs
모든 토큰이 적은 개수의 일부 expert로만 향하는 collapse 상황을 방지하기 위해, 일반적으로 각 expert는 buffer capacity가 고정되어있습니다. 처리할 수 있는 토큰 개수의 한계가 정해져있는 것입니다. 이에 따라 expert의 capacity가 가득 차 토큰이 가야하는 expert로 가지 못하고 drop 되는 상황이 발생하는데, 이렇게 drop되지 않고 성공적으로 적절한 expert에 할당되는 경우 success라고 칭합니다. 이 success rate를 효과적으로 잘 관리하는 것이 성공적이고 안정적인 MoE 학습의 지표가 된다고 합니다. 앞서 말씀드린대로 기존 방법론들은 이러한 collapse를 최소화하기 위해 여러 auxiliary loss를 적용하곤 했습니다. 이는 뒤에서 설명드릴 importance loss와 load loss입니다.
LIMoE의 경우 두 모달간의 토큰 개수 불균형이 심하기 때문에 더욱 collapse가 심해집니다. 텍스트 토큰은 단어 개수와 비슷할 것인데, 영상은 해상도가 작더라도 패치로 나누기에 토큰의 개수는 텍스트보다 최소 3배에서 17배 많게 됩니다. LIMoE는 멀티모달 모델이기에 각 expert가 특정 모달의 전문적인 구별력을 갖추도록 학습되길 기대할 수 있습니다. 이전 연구에서도 gating network가 이런 능력을 알아서 잘 학습하곤 했었는데, 지금과 같이 불균형적인 토큰 개수를 갖는 상황에서는 이를 기대하기 어렵습니다. 이러한 상황에서 expert의 buffer capacity에 의해 소수 모달인 텍스트 토큰은 모두 drop되어 제대로된 학습이 진행되지 않습니다. 토큰 특성이 비슷한 경우 비슷한 expert로 넘겨주는데, 영상 토큰과 텍스트 토큰은 gating function 입장에서 성질이 다르다보니 영상 토큰만 expert들에게 할당해도 capacity가 모두 차버리는 것이죠.
앞서 제가 기존 방법론들도 collapse 현상을 막기 위해 loss를 설계하였다고 했는데, 그 중 하나가 importance loss입니다. 수식적으로는 g(x)의 변동계수를 최소화해 토큰이 골고루 분산되도록 도와줍니다. 다시 멀티모달 상황을 살펴본다면, 이 importance loss가 최적화됨에도 올바른 학습이 이루어진다고 볼 수 없습니다. 만약 텍스트 토큰의 중요도가 낮아 모두 drop되고 영상 토큰만을 할당할 때 이 할당만 골고루 이루어진다면 loss의 최적화에는 문제가 없게됩니다. 하지만 텍스트 토큰이 모두 drop된다는 관점에서 학습이 제대로 이루어지지 않겠죠. 수식적으로는 바로 밑 항에서 설명드리겠습니다.
2.2.2 Auxiliary losses
앞서 말씀드린대로 기존에 활용되던 importance loss는 멀티모달 토큰을 동시에 입력받고 처리하는 LIMoE에 적용하기 어려움이 있습니다. 기존에 적용되던 importance loss와 load loss는 각각 아래 수식들과 같습니다.

위 수식은 importance loss로 가중치를 토큰의 importance라 두고 이 importance의 변동계수를 최적화함으로써 균형을 맞춰주게 됩니다. 선택받지 않은 expert의 가중치도 조절해준다는 것이 밑에서 설명드릴 load loss와의 차이점입니다.


위 수식은 load loss로 바로 윗줄에 있는 수식을 샘플의 load로 두고 마찬가지로 load의 변동계수를 최소화합니다. threshold는 top-k 중 k번째 가중치에 random noise \epsilon{}를 추가한 값이며 선택된 K개의 가중치 균형을 맞추는 loss에 해당합니다.
저자는 위 두 loss를 classic auxiliary loss라 칭하고 이에 두 가지 loss를 추가로 제안하여 멀티모달 상황에서의 학습 안정성을 도모합니다.
각 MoE layer에서, 각 모달리티 m에 대해 계산된 gating matrix G_{m} \in{} \mathbb{R}^{n_{m} \times{} E}를 추출합니다. n_{m}은 각 모달리티 토큰 개수를 의미하기 때문에 결국 각 토큰이 어떠한 expert로 향할지에 대한 확률을 담은 weight matrix라고 볼 수 있습니다. 방금 이야기한 행벡터는 p_{m}(\text{experts}|x) \in{} \mathbb{R}^{E}라 칭합니다. 이러한 상황에서 저자가 제안하는 local, global entropy loss는 아래 수식 (2)와 같습니다.



가장 위 수식 (2)에 local, global loss가 나타나있습니다. local loss는 모든 토큰의 weight entropy를 최소화하여 특정 expert로 토큰이 향할 수 있도록 도와줍니다. local loss만 최적화하면 특정 expert로 모든 토큰이 할당될 수 있기에 두 번째 수식과 같이 global loss는 해당 모달리티의 토큰을 평균낸 값의 entropy를 최대화합니다. 이를 통해 global 관점에서 토큰들이 global하게 할당될 수 있게 만들어주는 것입니다. 또한 모달별로 이 loss를 별도로 적용하기에 개수가 적은 텍스트 토큰의 drop 문제도 해결할 수 있게 됩니다.
3. Experiments
Training & Evaluation
학습은 LiT라는 zero-shot 모델과 동일한 3.6억 개의 영상-텍스트 쌍으로 진행하였습니다.
이후 평가 시에는 zero-shot 성능을 기본적으로 측정하였으며 ImageNet에 대한 image classification 성능과 MS-COCO 데이터셋에 대한 cross-modal retrieval 성능을 평가합니다. LIMoE를 타고 나온 feature를 대상으로 zero-shot 분류와 retrieval을 수행하는 것입니다. 이 뿐만 아니라 ImageNet에서 linear probing을 통한 10-shot accuracy를 측정합니다.
3.1 Controlled study across scales
우선 유사한 baseline으로 CLIP을 둘 수 있는데, 사실 CLIP을 학습시킨 데이터셋이 공개되어있지 않기도 하고 자잘한 tranining detail 차이가 커 직접적인 비교는 어렵다고 합니다. 따라서 저자는 MoE를 배제한 dense ViT (아래 그림에서 삼각형들)를 성능 비교 베이스라인으로 삼습니다. 또한 MoE layer에서 모두 k=1로 설정하였습니다.

Sparse(LIMoE)와 Dense 갈래 내부적으로는 모델이 커지고 FLOPs가 커짐에 따라 성능이 늘어날 것입니다. 중점적으로 봐야할 것은 동일 사이즈/패치 개수에 대한 Sparse와 Dense 간 연산량-성능 관계를 봐야겠죠. 우선 모든 모델 구조에 대해 cost-performance는 LIMoE가 Dense 모델들에 비해 압도적인 것을 볼 수 있습니다. 파라미터 개수가 일부 늘어나긴 하지만 늘어난 정도에 비해 성능 향상폭이 훨씬 크다는 의미입니다. 왼쪽과 가운데 그림에 해당하는 zero-shot과 10-shot ImageNet 분류 성능에 대해서는 평균적으로 각각 10.1%, 12.2%가 절대적으로 향상되었다는 점이 놀랍습니다.

표 3은 모델에 적용할 수 있는 loss의 적용 여부에 따른 ablation 성능입니다. 위에서부터 3개의 loss는 classic loss이고, 아래 4개는 LIMoE 저자가 제안한 loss입니다. 사실 경우의 수가 너무 많기 때문에 수행한 실험 중 특정 loss를 적용했을 때 또는 적용하지 않았을 때 다른 loss 적용 여부 관계 없이 가장 높은 성능을 적어두었다고 합니다.
우선 저자가 제안한 entropy loss와 관련해, 텍스트 모달에 대해서는 local과 global 모두에 대해 좋은 영향을 줍니다. 반대로 영상 모달에 대해서 global은 별 효과가 없고, local은 심지어 악영향을 주고 있습니다. 사실 지금 좀 고민되는 부분이 과연 영상의 모든 토큰을 MoE에 입력해주어 특정 expert가 해당 토큰의 특성을 알도록 할 필요가 있을까 싶은 상황인데, 영상의 local entropy를 최소화하는 것이 별 좋은 영향을 주지 못하는 점을 미루어 보아 제 실험을 할 때도 영상에서 필요한 토큰만 expert에 입력해주는 방식을 고민해볼 수 있을 것 같습니다.
4. Conclusion
모델 구조와 제안 내용이 간단하다보니 오히려 글을 길게 쓰려했던 것 같습니다. 현재 하고자 하는 연구는 우선 제가 다루는 Video Moment Retrieval task에서 아직 자연어 레벨로 텍스트 쿼리의 의미를 다루는 연구는 없어 LLM으로 gating function의 명시적 라벨을 만들어주어 텍스트 쿼리의 특성별 Expert를 만들어주려고 합니다. 잘 동작할지는 아직 실험중인데, 생각보다 application level에서 MoE를 활용하는 연구가 많이 없어 어려움을 겪고 있습니다. 대부분 위 논문과 같이 backbone 또는 MoE 시스템을 연구하는 논문들이 많네요
리뷰 읽어주셔서 감사합니다.
안녕하세요 김현우 연구원님 좋은 리뷰 감사합니다.
MoE 쪽은 처음 읽어보는데, 라우팅을 통해 적절한 expert를 지정해서 처리한다는
아이디어가 신기하네요. 읽다보니 몇가지 궁금한 점이 생겨 질문 남깁니다.
1. LIMoE는 모델의 일반성과 scalability를 높이기 위해 one-tower 구조를 가진다고 하셨는데, 하나의 인코더가 두 모달리티 토큰을 입력받으면 모달리티의 차이로 인한 문제점은 없나요? 인코더에 입력하는 텍스트 토큰과 이미지 토큰이 같은 형태이어야 할 것 같은데, 이 토큰은 어떻게 만들게 되나요?
2. softmax를 거치고 나서 expert의 기여도를 결정하는 가중치 값에 따라 활성화되는 expert가 다른 것으로 이해했는데, 이 때 작은 값의 weight를 가지는 expert의 경우 아주 조금만 활성화되는건가요 아니면 (threshold를 사용하던지 해서) 아예 활성화되지 않는 건가요? 가중치가 작더라도 모든 expert가 활성화되면 연산량 측면에서 효율적이지 못하지 않을까 하는 의문이 들어서 질문 드립니다.
감사합니다.
안녕하세요, 우선 답변이 늦어 죄송합니다.
1. 텍스트는 SentencePiece라는 자연어 처리 기법을 활용해 embed 해줍니다. 이후 text만의 Fc layer를 태워 d차원으로 만들어줍니다. 이후 이미지는 ViT 전처리와 동일하게 패치화 후 이미지만의 Fc layer를 태워 d차원으로 만들어줍니다. 이렇게 d차원으로 통일된 토큰들은 학습을 통해 자연스럽게 align이 맞아가도록 기대하는 상황입니다.
하나의 모델에 두 모달리티 토큰을 입력해도 문제가 없는지에 대해선, 제가 알기론 이와 같은 방식으로 성공적인 임베딩을 만든 방법론들이 기존에도 여럿 있었던 것으로 알고 있습니다. 그래서 두 모달의 토큰을 하나의 인코더에 넣어줘도 문제없이 잘 처리해주는 것은 가정으로 깔고 방법론을 구축한 것 같습니다.
2. 이해하시는 바는 맞고, 우선 활성화될 expert의 개수는 이미 정해져있습니다. K라는 하이퍼파라미터로, sparse MoE의 경우 보통 K=1, K=2를 사용합니다. 즉 여러 개의 expert 중 하나 또는 두 개의 expert만으로 forwarding을 하는 것입니다. E개의 expert가 있다고 했을때 사용할 전문가 개수 K=2를 예로 설명드리면, Softmax를 태우기 전 나온 E차원의 logit에 대해 가장 높은 두 개의 값을 제외하고 나머지엔 -inf를 채워주게 됩니다. 이렇게 채워준 후 softmax를 태우면 -inf 값은 0으로, 선택된 expert의 logit 합은 1로 변경됩니다. 이러한 방식으로 동작하여 결국 top-K 내에 선택되지 못한 expert는 아예 forward 되지 않으면서 연산량을 효율적으로 가져갈 수 있는 것입니다.
안녕하세요. 좋은 리뷰 감사합니다.
역시 구글이라서 그런지, 문제 정의와 이를 해결하고자 한 solution이 매우 확실한 것 같습니다. 하나 궁금한 점이 있는데, Auxiliary losses 파트가 본 논문에서 발생하는 문제 해결에서 매우 중요한 파트라고 이해하였습니다. 근데 선택받지 않은 expert의 가중치도 조절하는 것이 왜 collapse? 불균형을해결할 수 있는 건가요? 학습할 때 선택받은 expert만 뿐만 고려화면 불균형이 발생할 수 있으니까 선택받지 않은 expert 가중치도 고려하여서 불균형이 발생하지 않게 한다라고 이해하면 되는걸까요?
또한, threshold는 top-k 중 k번째 가중치에 random noise ϵ를 추가한 값이라고 하셨는데 random noise를 왜 추가한지가 잘 이해가 되지 않아 질문드립니다.
감사합니다.
안녕하세요 질문 감사합니다.
1. 선택받지 않는 expert의 가중치를 조정한다고 말씀드렸지만, 사실 전문가가 10개 일 때 10개에 골고루 routing될 수 있도록 해주는 loss입니다. 만약 importance loss는 없고 load loss만 존재한다면, 총 10개의 expert 중 선택된 2개의 expert에 대해서만 둘 중 하나에 치우치지 않고 골고루 가도록 학습됩니다. 여기서 선택되는 2개가 10개 중 골고루 선택되지 않고 특정 2개만 선택되는 상황(collapse)이 자연스레 발생한다고 합니다.
즉 10개의 전문가 관점에서는 10개에 골고루 rounting되도록 해주는 loss가 없기에, collapse를 발생시킬 수 있게 됩니다.
2. 저도 random noise의 존재 이유에 대해 찾아보았는데, MoE를 적용한 백본 논문 중 초창기의 방법론 하나가 이와 같은 noise를 추가함으로써 loss 학습의 안정성을 불러왔다고 밝혀 후속 연구에서도 자연스럽게 사용하는 기법이 되었다고 이해하였습니다.
감사합니다.