[CVPR 2024]Instance-Adaptive and Geometric-Aware Keypoint Learning for Category-Level 6D Object Pose Estimation

제가 이번에 리뷰할 논문은 Category-level의 6D Pose Estimation논문으로, Category-level의 방법론에서 Instance-Adaptive하게 keypoint를 예측하는 방식이라 하여 궁금해서 리뷰하게 되었습니다.

Abstract

Category-level의 6D Pose Estimation은 특정 카테고리 내의 미학습 인스턴스(동일 카테고리에 속하지만 형태가 다른 객체)의 rotation과 translation, size를 추정하는 것을 목적으로 합니다. Pose Estimation 분야는 이미지와 객체에 대응되는 대표적 형태(인스턴스들의 평균으로 구한 형태) 사이의 dense한 대응관계를 유추하는 방식을 통해 상당한 성능 개선을 이뤄왔으나, 형태가 크게 다를 경우 일반화 성능이 크게 떨어진다는 문제가 있습니다. 이를 해결하기 위해 저자들은 Instance-Adaptive and Geometric-Aware Keypoint Learning 방식을 제안하여 Category-level의 6D Pose Estimation 방법론인 AG-Pose를 제안하였습니다. 본 논문에서는 (1) 다양한 인스턴스에적응적으로 기하학적 구조를 표현하기 위한 Instance-Adaptive Keypoint Detection 모듈과 (2) 효율적으로 local 및 global한 기하학적 정보를 통합하기 위한 Geometric-Aware Feature Aggregation 모듈을 제안하였습니다. 저자들이 설계한 두 모듈을 통해 미학습 인스턴스에도 강인하게 keypoint를 에측함으로써 모델의 일반화 성능을 향상시켰으며, Category-level의 6D Pose Estimation에서 사용하는 벤치마크인 CAMERA25와 REAL275에서 제안한 AG-Pose의 성능이 Category별로 사전에 정의된 형태 정보를 사용하지 않고도 SOTA 방법론과 비교했을 때 우수함을 실험적으로 보였습니다.

Introduction

6D Pose Estimation은 대상 객체의 자세 정보를 추정함으로써 로봇의 manipulation이나 AR, 자율주행 분야에서 외부 물체와의 상호작용을 하기 위해 중요한 task입니다. 기존의 많은 연구들이 instance-level의 자세 추정 연구가 진행되었으나 이는 대상 객체에 대한 정확한 3D model(CAD)에 의존하여 다른 객체로의 일반화가 어렵다는 문제가 있었습니다. 이러한 문제를 해결하고자 CAD 모델을 사용하지 않고 특정 카테고리 정보를 포괄할 수 있는 Category-level의 연구가 등장하였으며, Category-level의 자세 추정 연구는 다양한 CAD 모델을 이용하여 특정 카테고리에 대하여 학습한 뒤, 학습에 사용하지 않은 다른 형태를 가진 인스턴스에 대해 자세를 추정하는 방식으로 이루어집니다.

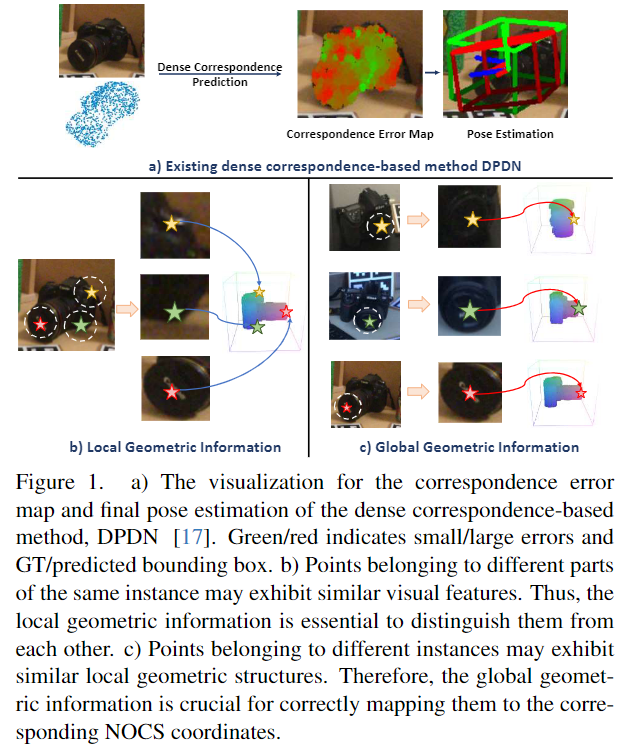
Category-level의 연구는 동일 카테고리에 속하지만 형태가 다양한 인스턴스들을 포함하며, 기존의 연구들은 대부분 이미지(RGB 또는 RGB-D)와 Noramlized Object Coordinate Space(NOCS, 인스턴스들의 평균적인 형태를 구하는 것이라고 이해하시면 됩니다) 사이의 dense한 correspondences를 설정하는 방식으로 연구되었습니다. 그러나 형태 변화가 클 경우에는 상관관계를 잘못 유추하는 경향이 있으며(Figure 1-a), 저자들은 이를 다양한 인스턴스의 기하학적 정보를 명시적으로 고려하지 않았기 때문이라고 분석하였습니다. Figure 1의 (b)는 시각적 특성이 비슷하지만 local한 영역의 기하학적 정보가 다는 경우이며, (c)는 local한 정보는 비슷하지만 전체 전체적인 카메라 형태가 다른 경우이며, 저자들은 이러한 예시를 통해 local 및 global한 기하학적 정보를 고려하는 것의 필요성을 이야기합니다.

저자들은 attention mechanism을 통해 모든 점의 특징을 집계하는 단순한 방식은 dense한 대응관계 계산을 위해서는 연산량의 오버헤드가 크다는 것을 이야기하며, 기존 방식과 다르게 sparse한 keypoint set을 이용하여 다양한 인스턴스의 형태를 표현하고, 기하학적 정보를 고려한 keypoint를 추출하여 대응 관계를 구축하는 것을 목표로 합니다. 저자들은 global한 기하학적 정보는 keypoint 사이의 상대적인 위치로 표현하고, local한 정보는 keypoint 주변 point와의 상대적 위치로 표현하고자 하였으며, 이때 인스턴스마다 다양한 형태를 모두 표현하기 위해 adaptive하게 인스턴스의 keypoint를 예측하고 새로운 인스턴스에서 일반화를 위해 local 및 global한 기하학적 정보를 효과적으로 인코딩할 수 있도록 네트워크를 설계합니다.

본 논문에서는 novel Instance-Adaptive and Geometric-Aware Keypoint Learning 방식을 제안하였으며, 인스턴스에 따라 형태가 다양한 경우에 대응하기 위해 adaptive하게 keypoint를 생성하는 Instance-Adaptive Keypoint Detection(IAKD) 모듈과 local 및 global한 기하학적 정보를 효율적으로 추출하기 위한 Geometric-Aware Feature Aggregation(GAFA) 모듈을 설계하여 강력한 keypoint 수준의 대응 관계를 구축하였다고 합니다.

본 논문의 contribution을 정리하면,

• Category-level의 6D Pose Estimation을 위한 새로운 학습 방식을 제안하였으며, 이를 통해 형태 변화가 큰 미학습 인스턴스에 대해서도 잘 일반화 할 수 있도록 함. 저자들에 따르면 keypoint를 adaptive하게 결정하는 최초의 연구라 함.
• Category-level의 연구에서 주로 사용되는 CAMERA25와 REAL275 벤치마크에서 각 인스턴스에 대한 3D 형태를 reconstruction하는 SOTA 방법론보다 우수한 성능을 달성함.

Methods

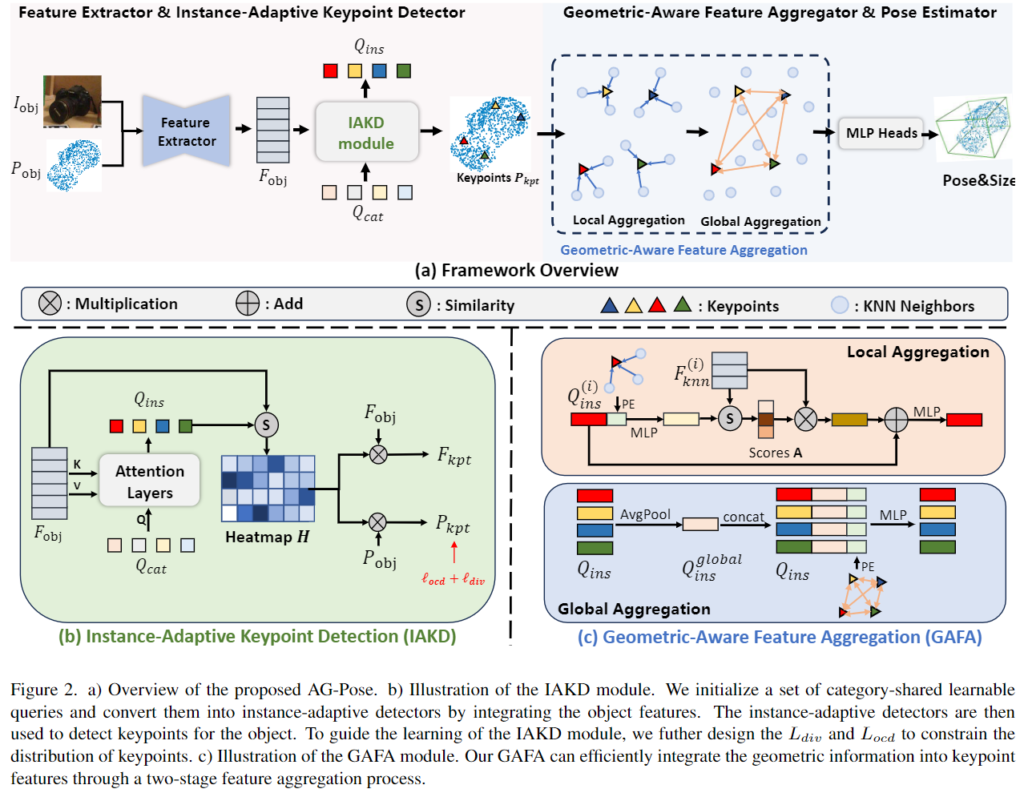
A. Overview

RGB-D이미지가 주어졌을 때 MaskRCNN을 이용하여 대상 객체에 대한 segmentation mask와 대상 객체를 중심으로 crop한 RGB 이미지 \mathbf{I}_{obj} \in \mathbb{R}^{H⨉W⨉3}, crop된 영역의 depth 정보와 intrinsic 파라미터를 이용하여 구한 point cloud \mathbf{P}_{obj} \in \mathbb{R}^{N⨉3}(N은 point의 개수)를 구합니다. 이후 \mathbf{I}_{obj}와 \mathbf{P}_{obj} 를 입력으로 하여 대상 객체의 rotation \mathbf{R}과 translation \mathbf{t}, size \mathbf{s}을 추정합니다. AG-Pose는 위의 Figure 2의 (a)에서 확인할 수 있으며, 크게 Feature Extractor, IAKD 모듈, GAFA 모듈로 구성됩니다.

B. Feature Extractor

Point cloud를 이용하는 3D task에서 많이 사용되는 PointNet++을 이용하여 \mathbf{P}_{obj}로부터 point feature \mathbf{F}_p \in \mathbb{R}^{N⨉C_1}를 추출하고, segmentation 분야에서 제안된 픽셀 수준의 정보를 얻을 수 있는 PSPNet을 이용하여 \mathbf{I}_{obj}로부터 feature를 추출한 뒤, \mathbf{P}_{obj}에 대응되는 픽셀에 대한 정보를 모아 RGB feature \mathbf{F}_I \in \mathbb{R}^{N⨉C_2}를 구한 뒤, \mathbf{F}_p와 \mathbf{F}_I를 concat하여 \mathbf{F}_{obj} \in \mathbb{R}^{N⨉C}를 다음 네트워크로 입력합니다.

C. Instance-Adaptive Keypoint Detector(IAKD)

앞서 introduction에서 이야기한 내용과 같이 local 및 global한 기하학적 정보를 활용하는 것이 중요하지만 단순히 attention mechanism을 적용할 경우 dense한 point들 사이의 특징을 집계할 경우 연산에 비용이 너무 많이 든다는 문제가 있습니다. 따라서 sparse한 keypoint를 활용하고자 하였으나 인스턴스마다 다양한 형태를 가지며 inference 과정에는 정확한 3D 형태에 접근할 수 없다는 한계가 있습니다. 또한 keypoint를 설정하기 위해 기존에 방법론에서 사용하던 FPS(Fartest Point Sampling)방식의 경우 정확한 3D 형태를 접근할 수 없어 발생하는 노이즈에 대응하지 못한다는 한계가 있습니다. 이러한 한계를 극복하기 위해 본 논문에서는 인스턴스에 adaptive하게 keypoint를 감지하는 IAKD 모듈을 설계하였습니다.

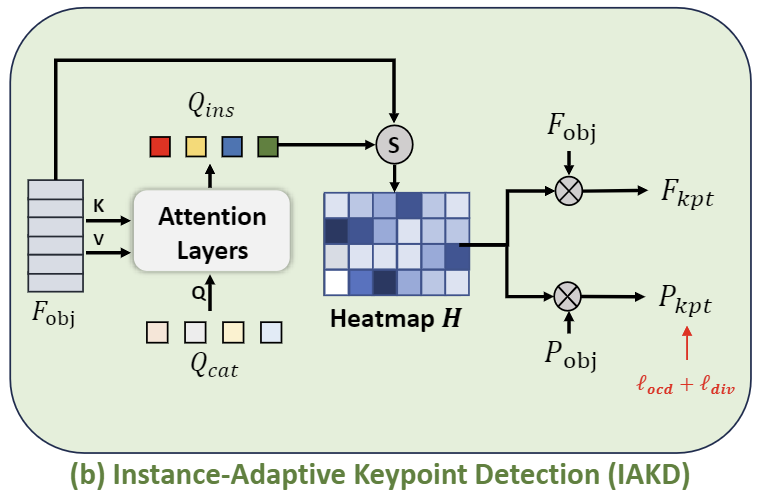
위의 그림이 IAKD 모듈의 파이프라인으로, 먼저 Category별로 학습 가능한 Queries \mathbf{Q}_{cat} \in \mathbb{R}^{N_{kpt}⨉C}를 초기화합니다. 여기서 \mathbf{Q}_{cat}은 keypoint detector의 역할을 하고(해당 Query별로 하나의 keypoint를 구하기 위한 쿼리 정보가 되는 것 입니다) 카테고리끼리 공유하므로 category-shared dectector라 합니다. 이후 Transformer layer를 통해 객체에 대한 feature를 융합하여 category-shared detector를 instance-adaptive detector \mathbf{Q}_{ins} \in \mathbb{R}^{N_{kpt}⨉C}로 변환합니다.

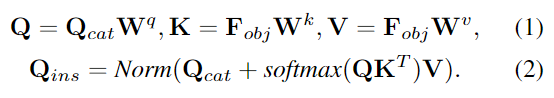
이후 \mathbf{Q}_{ins}와 \mathbf{F}_{obj} 사이의 코사인 similarities를 계산하여 keypoint heatmap \mathbf{H} \in \mathbb{R}^{N_{kpt}⨉N}을 구한뒤, 가중합을 통해 3D keypoint \mathbf{P}_{kpt} \in \mathbb{R}^{N_{kpt}⨉3}와 대응되는 feature \mathbf{F}_{kpt} \in \mathbb{R}^{N_{kpt}⨉C}를 구합니다.

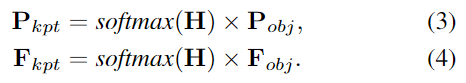
객체의 기하학적 정보를 표현하기 위해 keypoint는 객체의 표면에 잘 분포되어야 하며, 이를 명시적으로 학습하지 않을 경우 keypoint가 표면이 아닌 위치나 특정 위치에 밀집되는 문제가 발생할 수 있습니다. 따라서 저자들은 keypoint가 서로 다른 영역에 분포하도록 유도하기 위해 diversity loss L_{div}를 추가로 설계합니다. Diversity loss는 아래의 식(5)로 정의되며, th_1은 하이퍼파라미터이며, \mathbf{P}^{(i)}_{kpt}는 i번째 keypoint를 나타냅니다. 즉, 서로 다른 keypoint 사이의 거리가 th_1보다 커지도록 loss를 설계한 것입니다.

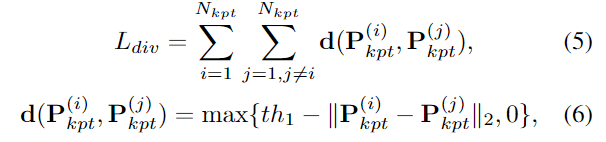
또한, keypoint가 객체의 표면에 존재하도록 하고 노이즈를 제거하기 위해 object-aware chamfer distance loss L_{ocd}를 설계하여 keypoint의 분포를 제한하였다고 합니다. 먼저 GT pose와 size 정보를 활용하여 point cloud \mathbf{P}_{obj}를 변환한 뒤, 객체에 대한 3D 모델 \mathbf{M}_{obj} \in \mathbb{R}^{M⨉3}을 기반으로 노이즈를 제거한 \mathbf{P}^*_{obj}를 구합니다.

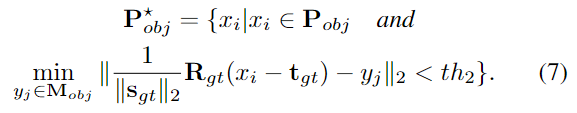
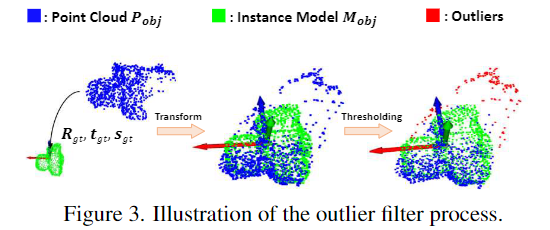
위의 Figure 3이 outlier를 제거한 \mathbf{P}^*_{obj}를 구하는 과정이며 object-aware chamfer distance loss는 아래의 식 (8)로 정의됩니다. 이를 통해 네트워크는 키포인트를 \mathbf{P}^*_{obj}에 가까워지도록 예측하고, 이상치를 필터링하는 방식을 학습할 수 있었다고 합니다.

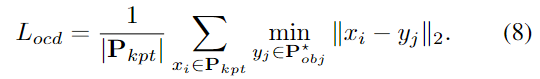
D. Geometric-Aware Feature Aggregator(GAFA)

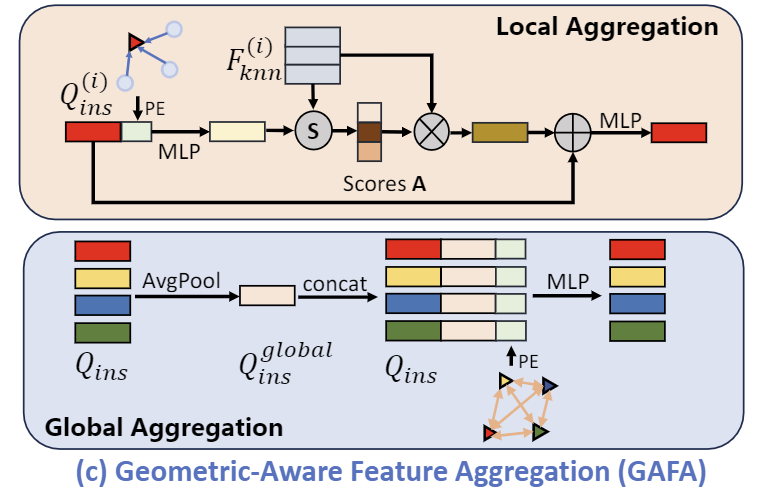
저자들은 Keypoint에 기하학적 정보를 효율적으로 통합하기 위한 Geometric-Aware Feature Aggregation 모듈을 제안하였습니다. GAFA 모듈은 local aggregation과 global aggregation 2단계로 이루어지며 위의 그림이 GAFA 모듈의 개요입니다. 먼저, 각 keypoint에 대해 \mathbf{P}_{obj}와 \mathbf{F}_{obj}로부터 K개의 nearest neighbors points \mathbf{P}_{knn} \in \mathbb{R}^{N_{kpt}⨉K⨉3}와 features \mathbf{F}_{knn} \in \mathbb{R}^{N_{kpt}⨉K⨉C}를 선별합니다. global한 기하학 정보f_g는 keypoint 사이의 위치 관계로 표현하고, local한 기하학적 정보f_l는 keypoint와 인접한 point 사이의 상대적 위치 정보를 이용하여 표현합니다. f_l과 f_g는 아래의 식으로 구할 수 있습니다.

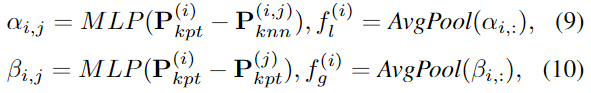
이후 local한 기하학적 정보를 keypoint에 통합하기 위해 keypoint에 대한 feature \mathbf{Q}_{ins}와 f_l를 결합하고, 융합된 정보와 이웃 point 사이의 상관관계 score \mathbf{A}를 계산하여 가중합하여 local feature를 구합니다.

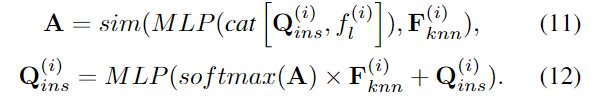
또한 객체의 전체적인 기하학적 특성을 반영하기 위해 keypoint feature와 global한 기하학적 정보 f_g를 융합합니다. 먼저 keypoint에 대한 feature \mathbf{Q}_{ins}에 대하여 Average Pooling을 적용하여 keypoint feature에 대한 global feature \mathbf{Q}^{global}_{ins} \in \mathbb{R}^{1⨉C}를 구한 뒤, 각 keypoint feature에 f_g와 함께 융합합니다.

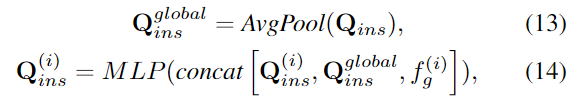
이러한 두 단계를 통해 keypoint에 대하여 local한 기하학적 정보와 global한 기하학적 정보를 adaptive하게 융합합니다.

E. Pose & Size Estimator

이후 pose를 추정하는 과정은 기존 연구의 방식으르 따라 keypoint에 MLP를 적용하여 NOCS의 좌표를 추정한 뒤, regression을 통해 최종 pose와 size 정보 \mathbf{R, t, s}를 예측합니다.

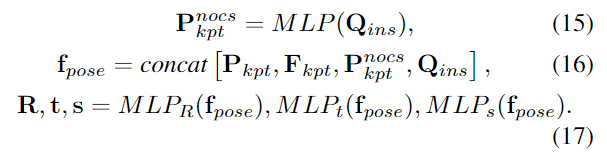
F. Loss Function

total loss는 아래의 식 (18)로 정의되며, \lambda는 하이퍼파라미터로 해당 논문에서는 각각 1.0, 5.0, 1.0, 0.3으로 설정하였다고 합니다.

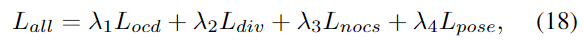
이때, L_{pose}는 GT pose와 scale에 대하여 L1 loss를 적용하여 구합니다.

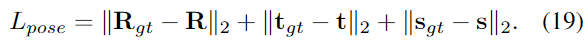
L_{nocs}는 point cloud를 GT Pose와 scale을 이용하여 NOCS로 투영시켜 구한 뒤, keypoint들에 대하여 SmoothL1 loss를 적용하여 구합니다.

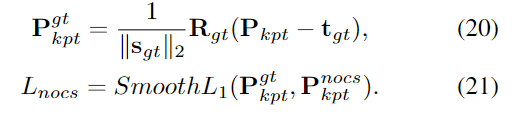
Experiments

Dataset and Evaluation metrics

Category-level의 연구에서 가장 널리 사용되는 CAMERA25와 REAL275 데이터 셋을 이용하여 실험을 진행합니다.

• CAMERA25
  : 6가지 Categories에 대한 1,085개의 인스턴스로 구성된 데이터로, 300K개의 합선 RGB-D 데이터로 구성
  184개의 인스턴스에 대한 25,000장의 이미지로 평가
• REAL275
  : Real 데이터로, CAMERA 25와 동일한 Categories로 구성
  13개의 scene에 대하여 7K개의 이미지로 이루어져있으며, 카테고리당 3개의 미학습 인스턴스를 포함한 6개의 scene를 평가에 사

평가지표는 기존 방법론과 동일하게 3D IoU와 n° m cm를 평가지표로 이용하였습니다.

• 3D IoU
  : 3D bounding box의 IoU가 50%와 75% 이상일 경우 정답으로 보아 평균 정밀도를 구함
• n° m cm
  : rotation과 translation 오차를 직접적으로 구하여 오차각이 n° 이하, 오차거리가 m cm 이하일 경우 정답으로 간주

Comparison with SOTA Methods

< Results on REAL275 >

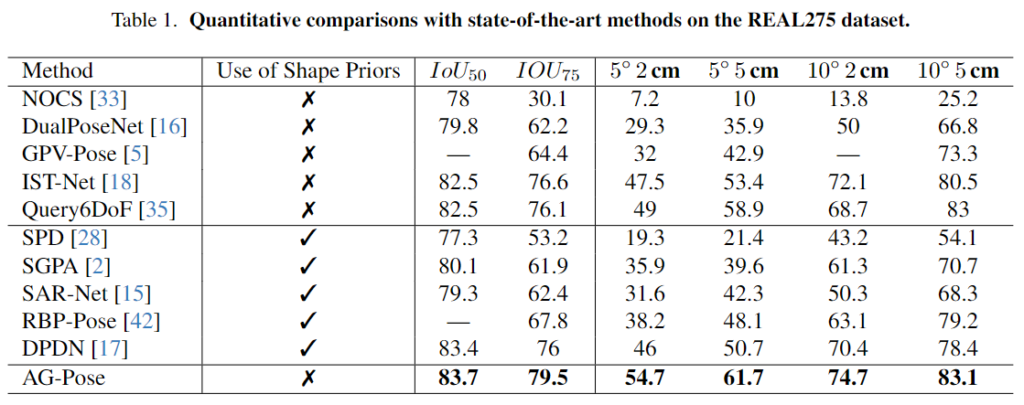
위의 Table 1은 REAL275 데이터에서 SOTA 방법론들과 비교한 결과로, 모든 평가지표에서 저자들이 제안한 방식이 가장 좋은 성능을 달성하였습니다. Shape Priors는 Category-level 연구에서 각 인스턴스에 대한 3D 형태를 reconstruction하는 것을 의미하며, 저자들은 이러한 과정 없이도 자신들이 더욱 좋은 성능을 달성하였음을 어필합니다.

< Results on CAMERA25 >

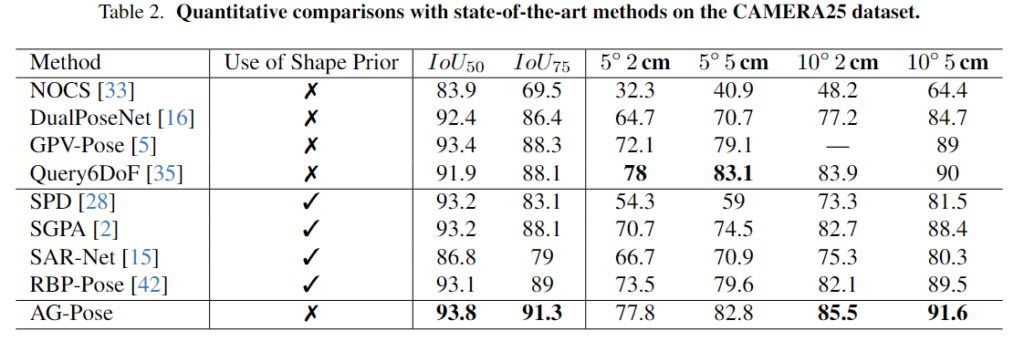
Table 2는 CAMERA25 데이터에 대한 SOTA 방법론과의 비교 실험 결과로, 대부분의 평가지표에서 SOTA를 달성하였으나, 일부 항목에서는 Query6DoF가 더 좋은 성능을 보였으나, 비슷한 성능을 달성하였음을 어필합니다. 마찬가지로 Shape Prior를 사용하는 타 방법론과 비교했을때는 더 좋은 성능을 달성한 것을 확인하실 수 있습니다.

< Results on Correspondence errors >

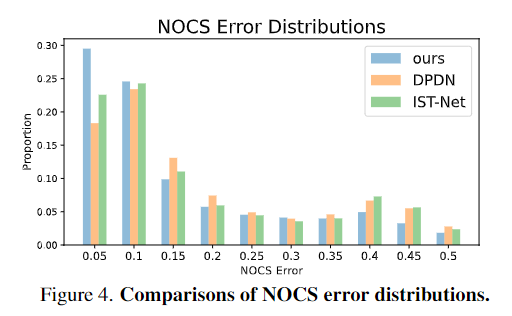
Figure 4는 keypoint-level의 대응 관계가 조밀함을 검증하기 위해 REAL275 데이터셋에서 DPDN과 IST-Net 방법론과 저자들의 방법론을 NOCS에서의 error 분포를 계산한 것 입니다. 오차 분포가 AG-Pose(ours)는 더 낮은 값에 집중되어있음을 통해 AG-Pose에서 생성한 keypoint가 미학습한 instance에서 더 일반화 성능이 좋다는 것을 어필합니다.

Ablation Studies

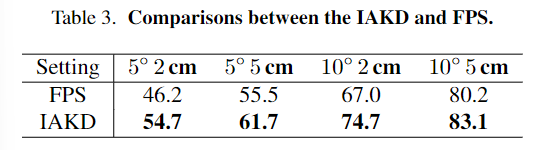
• Table 3을 통해 IAKD 모듈의 효율성을 확인하실 수 있습니다. instance별로 adaptive한 keypoint를 생성하므로써 FPS 방식을 이용할 때 보다 성능이 확연히 개선되었습니다.

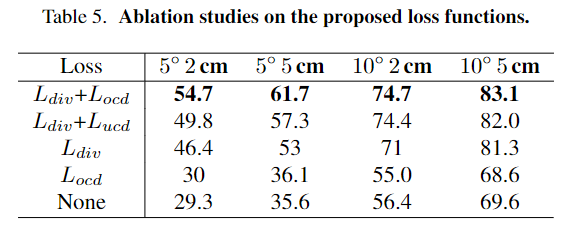
• Table 5는 저자들이 제안한 loss에 대한 효과를 확인한 실험입니다. L_{div}와 L_{ocd}를 도입하므로써 성능이 크게 개선된 것을 확인할 수 있습니다. (L_{div}는 keypoint가 한 영역에 집중되지 않도록 설계된 loss이며, L_{ocd}는 keypoint가 표면에 존재하도록 설계한 loss로 노이즈를 필터링하는 과정이 포함됩니다.)
• L_{ucd}는 normal chamfer distance loss로 노이즈를 제거하는 과정이 없으며, 위의 두 행의 실험 결과를 통해 이상치를 제거하는 과정의 효과도 확인할 수 있습니다.

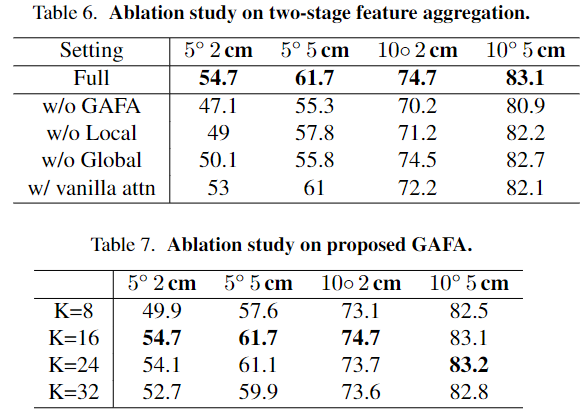
• 위의 Table 6은 기하학적 정보를 융합하는 과정의 효과를 실험적으로 검증한 것으로, Local aggregation과 Global aggregation이 효과적임을 확인할 수 있습니다.
• Table 7은 local aggregation에 사용하는 이웃한 point의 개수에 따른 성능을 확인한 것으로, K=16일 때 가장 좋은 성능을 보이는 것을 확인할 수 있습니다.
• vanilla attention에 대해서 연산량을 비교한 결과는 따로 없어서 아쉽습니다..