안녕하세요, 서른여섯 번째 X-Review입니다. 이번 논문은 2023년도 NeurIPS에 게재된 Scale-Space Hypernetworks for Efficient Biomedical Imaging입니다. 논문제목도 그렇고 본문에서도 medical이라는 단어가 많이 나오는 것을 보아 의학쪽 논문인 것 같네욤. . . 바로 시작하도록 하겠습니다. 🦉

1. Introduction

CNN은 medical 이미지 분석쪽에서 많이 사용되고 있는데, 메디컬 어플리케이션에서 사용하려고 하니 resource는 제한됐는데, computation cost가 너무 많이 들어서 사용하기 힘들다고 합니다. 그래서 모델의 정확도를 유지하면서 computation cost를 낮추는 연구가 많이 있어왔는데요. 예를 들어 parameter 수와 convolution kernel 크기를 줄이는 데 초점을 맞춘 quantization, pruning, factoring 등이 있겠습니다. 그런데 이들은 모두 모델의 정확도와 계산 효율성 사이의 trade-off를 고려해야 했죠. 이를 위해서 많은 모델을 학습하고 이들의 trade-off를 다 고려하여 최적의 모델을 선정해야 합니다.

본 논문에서는 의료 이미지 모델, 특히 U-Net과 같은 네트워크의 계산 효율성을 향상시키는 새로운 접근 방식을 제안합니다. U-Net과 같은 네트워크라 함은 이미지의 feature를 다양한 shape으로 resize하는 ,,,, 그런 네트워크를 의미합니다. 기존에 아키텍처는 spatial scale을 2라는 고정된 수로 줄였는데(32 → 16 → 8 같은 느낌 .. ) 본 논문에서는 이 scale factor는 보다 연속적으로 변화시킬 수 있는 더 일반적인 모델 아키텍처를 연구하였습니다.

이런 방식으로 중간 feature의 크기를 resize함으로써, 모델을 학습하고 inference할 때 필요한 computation cost를 줄일 수 있겠습니다. 하지만 다양한 rescaling factor에 대한 모델을 일일이 학습하는 것은 또 많은 리소스를 필요로 하겠죠. 이에 대한 해결책으로 본 논문은 Scale-Space Hypernetworks (SSHN)이라는 새로운 하이퍼네트워크 학습 프레임워크를 제안합니다. 이 프레임워크를 사용하면 기존처럼 여러 모델을 개별적으로 학습하는 대신, 단 하나의 모델을 사용해서 다양한 rescaling ratio에 대응할 수 있는 모델들의 전체 set을 학습할 수 있게 됩니다.

SSHN 모델은 기본적으로 하나의 모델을 학습했지만, 학습 후에는 이 모델을 활용해 다양한 이미지 크기에 따른 정확도와 속도 사이의 trade-off를 빠르게 비교할 수 있습니다. 이 과정에서 모델은 각 setting에 대해 얼마나 효율적인지, 얼마나 정확한지를 계산해서 최적의 trade-off 지점을 찾아내는데 도움을 줄 수 있죠.

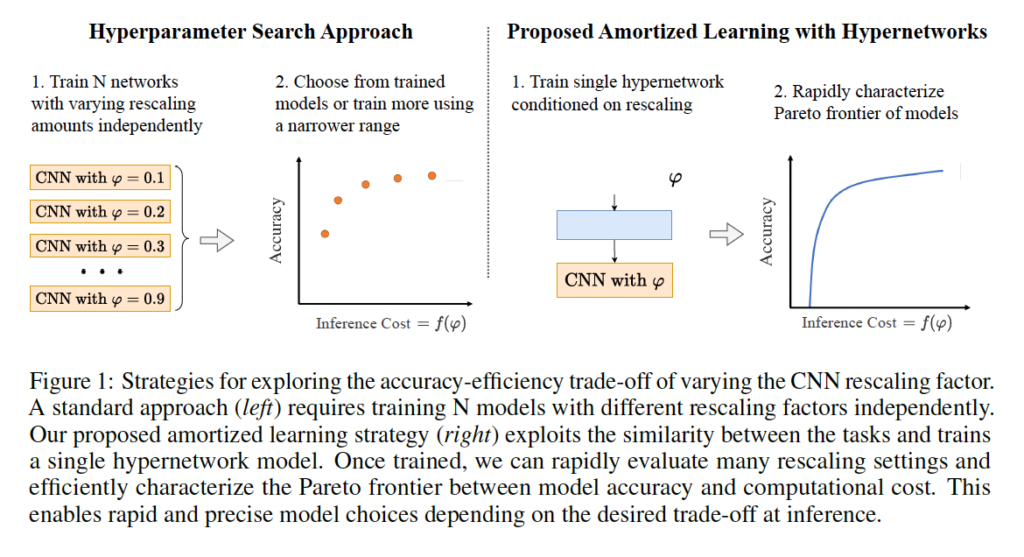
이 과정은 위 그림1에 나와있는데요, 그림의 왼족 부분에서 볼 수 있 듯, 전통적인 방식은 여러 모델을 각각 따로 학습시켜야 했기 때문에 많은 시간과 리소스를 필요로 했습니다. 매번 새로운 설정으로 모델을 조정하고 학습하는데는 한계가 존재하겠죠.

반면에,, 오른쪽 부분에 있는 SSHN은 단 한 번의 학습으로 여러 rescaling set을 다룰 수 있습니다. 이 하이퍼네트워크 모델은 한 번 setting하면 다양한 크기 조절에 쉽게 적응해서 필요에 따라 각각의 setting을 빠르게 평가하구 최적의 선택을 할 수 있게 도와줍니다.

이런 점에서 SSHN 모델은 큰 이점을 제공하는데요, 예를 들어 의료 환경에서 빠른 진단이 필요한 경우에는 속도를 우선으로 할 수 있고, 더 정밀한 분석이 요구될 때는 정확도를 우선으로 설정할 수 있겠습니다. 즉, 각각의 상황에 맞게 적절한 이미지 크기와 처리 방식을 선택할 수 있다는 것입니다.

본 논문의 contribution은 다음과 같습니다.

1. Scale-Space HyperNetworks (SSHN)이라는 새로운 개념의 모델을 제안. 본 모델은 주어진 rescaling 비율에 따라 영상의 spatial resolution을 조절하는 layer의 weight를 예측. 중간 feature의 spatial dimension을 줄임으로써 결과적으로 모델의 inference cost를 줄일 수 있다.
2. 본 모델을 여러 의료 영상 분석 task에 적용해본 결과, 기존 방법론들보다 훨씬 빠르며, 모델의 accuracy와 inference time 사이의 최적의 trade-off를 선정하기 쉽니다.
3. 본 모델을 여러 의료 영상 분석 task에 적용해본 결과, 서로 다른 cost를 갖는 rescaling factor가 비슷한 성능을 낸다는 점을 발견하였다. SSHN을 사용하여 모델의 accuracy를 낮추지 않고도 FLOPs를 최대 50%까지 줄일 수 있음을 보여준다.
4. 다양한 rescaling factor를 갖는 하나의 모델을 학습하는 것은 일종의 regularization 효과를 갖고 있어서, 고정된 rescaling factor로 학습한 모델보다 본 논문에서 제안한 방법을 사용하면 모델의 정확도를 일관되게 향상시킬 수 있다.

2. Scale-Space HyperNetworks

이제 저자가 제안한 Scale-Space HyperNetworks에 대해 자세히 살펴보도록 하겠습니다. 기본적으로 CNN은 input으로 x를 받아서 output값 \hat{y}를 예측해냅니다. 이 과정에서 모델은 주어진 데이터셋 D에 대해 loss 함수 L을 최소화하는 방향으로 파라미터를 최적화해나가죠. 예를 들어, 지도학습의 경우에서는 아래 식 1과 같습니다.

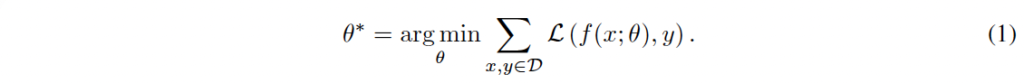
이 때, 대부분의 CNN은 고정된 rescaling factor를 사용해서 중간 feature의 spatial size를 조절합니다. 일반적으로 각 feature의 shape을 반으로 줄이거나 두 배로 늘린다는 의미입니다. 하지만, 본 논문에서는 연속적인(continous한) rescaling factor \varphi ∈ [0, 1]를 사용해서 feature shape을 조정할 수 있는 CNN 모델 f_{\varphi}(x; \theta)를 정의합니다. 이 모델f_{\varphi}(x; \theta)은 기존 CNN 모델 f(x; \theta)과 동일한 파라미터와 연산을 사용하지만, 중간 feature의 rescaling operation은 \varphi에 의해 결정됩니다. 예를 들어보자면 기존 이미지 모델의 downsampling layer R(x)는 입력 tensor (C,H,W)를 output tensor (C, H/2, W/2)에 매핑합니다. 이와 반대로 저자가 제안한 R_{\varphi}(x)의 resizing layer같은 경우는

(C, [\varphiH],[\varphiH]) shape을 갖는 output tensor가 생성됩니다.</p> <p style="caret-color: rgb(0, 0, 0); color: rgb(0, 0, 0); font-style: normal; font-variant-caps: normal; font-weight: 400; letter-spacing: normal; orphans: auto; text-align: start; text-indent: 0px; text-transform: none; white-space: normal; widows: auto; word-spacing: 0px; -webkit-text-size-adjust: auto; -webkit-text-stroke-width: 0px; text-decoration: none;">기존 기법을 사용해서 rescaling factor [latex]\varphi

의 함수로써 모델의 정확도를 확인하기 위해서는 각 rescaling factor에 대해 여러 f_{\varphi}(.; \theta) instance를 학습해야 하므로 상당한 computation cost가 발생합니다. 대신에, 본 논문에서는 하이퍼네트워크라고 불리는,,, rescaling factor \varphi를 학습하는 것을 통해 parametric 함수 f_{\varphi}(.; \theta)를 동시에 학습하는 프레임워크를 제안했습니다. 학습 가능한 파라미터 w를 갖는 함수 h(\varphi;w)를 사용해서 rescaling factor를 함수 함수 f에 대한 convolution weight set에 mapping합니다. 이런 방식을 통해 모델은 다양한 rescaling factor를 한 번에 학습함으로써 computation cost를 크게 줄일 수 있습니다.

즉, 정리해보자면,, 하이퍼네트워크라는 일종의 신경망을 제안을 했는데 이 하이퍼네트워크의 역할은 어떤 신경망이 다양한 상황이 주어질 떄 어떻게 행동해야 할 지를 학습하는 것으로 보면 되겠습니다. 여기서는 image의 scale을 조정할 때 사용되고 이쓴ㄴ데 이미지를 작게 만들거나 크게 만들때마다 그에 맞게 신경망이 어떻게 반응해야 할지를 결정하게 됩니다. 그래서 하이퍼네트워크가 이런 상황에서 신경망에게 이미지 크기에 맞는 적절한 scaling factor를 알려주기 위해 입력으로 rescaling factor를 받아서 이 비율에 맞는 새로운 가중치를 만들어내고, 이렇게 만들어낸 가중치 w가 이미지 크기가 변경될 때마다 모델이 최적의 성능을 낼 수 있도록 도와줍니다.

파라미터 w는 위 식 2에 있는 목적함수에 기반하여 학습하면서 최적화됩니다.

학습할 때 각 iteration에서 \varphi ~ p(\varphi) 중에서 무작위로 rescaling factor를 선택하게 됩니다. 이 rescaling ratio는 신경망 내부의 표현과 주 네트워크의 weight를 결정합니다. 하이퍼 네트워크를 통해 주 신경망 가중치가 생성되는 것입니다.

하이퍼네트워크는 주 신경망에 비해 더 많은 learnable 파라미터를 갖고 있지만, convolution 파라미터의 수는 같습니다. 추론 시에는 하이퍼네트워크를 사용하지 않고 주어진 \varphi 에 대해 예측된 weight만 사용하여 주 신경망이 동작하기 때문에, inference 때에는 computation cost가 덜 들게 되는 것이죠.

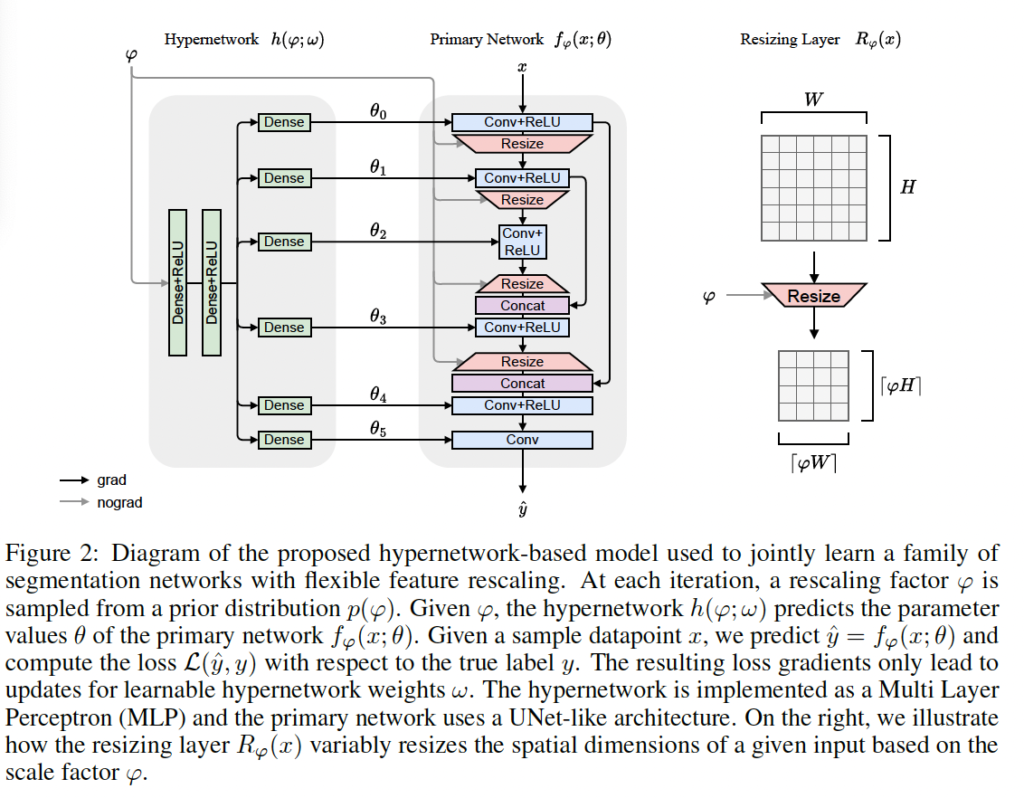
하이퍼 네트워크는 FCN Network이며, 주 네트워크는 medical task에서 주로 사용되는 UNet과 유사한 구조를 사용합니다. 그림 2는 Scale-Space HyperNetworks가 적용된 세 단계의 U-Net 아키텍처를 보여줍니다.

그림을 보시면 크게 hypernetwork와 primary network로 나뉘는데요, 매 iteration 마다 rescaling factor가 사전에 정의된 분포 내에서 smapling되어 사용되게 됩니다. 입력 데이터 x가 네트워크로 들어가고 모델이 예측해낸 값이 \hat{y}라고 할 때 loss 함수는 L(\hat{y}, y)가 되겠죠. 이때 loss gradient는 오직 learnable한 하이퍼파라미터 가중치 w에 의해서만 update되게 됩니다. hypernetwork는 MLP로 구현이 되어 있으며, 주 네트워크는 앞에서 언급했듯이 UNet과 유사한 구조를 갖고 있습니다. 사용되는 resizing layer는 bilinear interpolation입니답.

3. Experimental Setup

3.1 Tasks

실험은 segmenation과 registration 두 task에 대해서 수행되었습니다.

Segmentation

segmentation task에서 주 신경망은 input x를 받아 segmention map y를 출력해냅니다. 지도학습을 사용하였으며 L(\hat{y}, y) 손실함수를 사용하였는데 \hat{y}는 예측된 segmentation map이구요. 손실함수는 cross entropy loss를 사용해서 학습한 다음 soft Dice-score loss를 사용해 fine-tuning하였습니다.

• Dice(y; ^y) = (2|y ∩ ^y|) / (|y| + |^y|)

Registration

registration task에서는 moving image x_m를 fixed image x_f에 맞춰 registration합니다. 사용한 loss 함수는 아래와 같습니다.

• L = Lsim(xm * θ; xf) + λreg * Lreg(θ)

L_{sim}는 MSE, L_{reg}는 total variation입니다.

3.2 Datasets

실험에서는 4가지의 다양한 biomedical 이미지 데이터셋을 사용하였습니다. 구체적으로는 뇌 MRI scan한 데이터셋인 OASIS와, 머리 하반부 X-ray scan을 포함한 데이터셋인 PanDental, 초음파 데이터셋인 CAMUS와 백혈구 현미경 영상 데이터셋인 WBC입니다.

각 데이터셋에 대해서는 학습 64%, 검증 16%, test 20% 비율로 나눠서 학습하구 평가했다고 합니다.

3.3 Baseline Methods

본 논문의 모델은 3가지의 다른 방식과 비교해서 효율성과 정확성을 평가하였습니다.

Fixed

fixed 방식은 고정된 rescaling factor를 갖는 일반적인 U-Net 모델을 학습한 것입니다. 실험할 때 0~ 0.5까지 0.05간격으로 rescaling factor를 조정해가며 학습하였습니다.

Stochastic

stochastic 방식은, 확률적인 rescaling factor를 사용해서 학습한 것인데요, 마찬가지로 U-Net 모델을 사용하였구 rescaling factor는 학습 도중 확률적으로 sampling 되게 됩니다.

FiLM

마지막으로 FiLM은 Feature-wise Linear Modulation인데요. 이건 convolutional model을 조절할 수 있는 모듈입니다. 자세히는 모르겠지만, input을 곱셈 및 덧셈 벡터로 매핑해서 네트워크의 다양한 지점에서 중간 feature map을 affinely transform하는데 사용한다고 합니다. rescaling factor는 마찬가지로 학습할 동안 확률적으로 sampling되게 됩니다.

3.4 Experimental Details

Primary Network Architecture

기본 네트워크 구조로는 U-Net 아키텍처를 사용하였습니다. 그 이유로는 U-Net이 의료 영상 분석 쪽에서 널리 사용되고 있는 아키텍처 중 하나이기 때문이라고 합니다. 본 네트워크는 rescaling factor에 따라 downsampling 혹은 upsamping을 학 ㅣ위해 bilinear interpolation layer를 사용하였습니다. U-Net 네트워크는 5개의 encoder layer와 4개의 decoder layer로 구성되는 U자 모양을 하고 있는 네트워크입니다.

Evaluation

각 실험 setting에 대해 random seed를 각각 다르게 한 다음 다섯 번 실험을 한 결과의 평균과 표준편차를 리포팅하였습니다. 학습이 끝난 후 하이퍼네트워크를 사용해 0.01 간격으로 rescaling factor에 따른 성능 및 speed를 평가하였습니다. 이 점은 기존의 고정된 model을 사용할 때보다 더 세밀한 평가가 가능하다고 볼 수 있는데, 기존에는 각 rescaling factor에 대해 별도의 모델을 학습학 凸평가했어야 했기 ㄸ때문입니당.

4. Experimental Results

4.1 Accuracy and Computational Cost

이제 실험 결과에 대해 살펴보도록 하겠습니다. 첫 번째 실험은 하이퍼네트워크를 통해 생성된 segmentation model의 정확도와 효율성을 평가하구, 이 모델과 fixed rescaling factor를 사용하여 생성된 모델과 비교하고 있습니다.

Accuracy

본 모델은 다양한 rescaling factor에 대해 주 네트워크의 weight를학습하고, 이 weight를 사용하는 모델의 성능을 특정 resclaing factor로 독립적으로 학습한 모델과의 성능을 비교한 결과를 살펴보도록 하겠습니다.

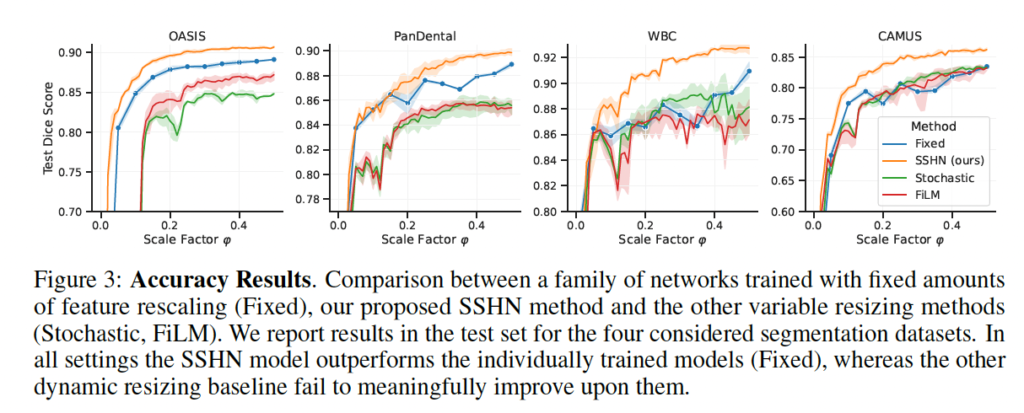
위 그림3은 4개의 각 데이터셋에서의 segmentation 성능을 나타낸 그래프입니다. 그래프 중 주황색 line이 본 논문에서 제안한 SSHN이고, 파란색이 기존 우리가 알고 있는 고정된 rescaling factor를 사용한 성능이며, 빨간색 초록색이 각각 위에 베이스라인 설명드릴 때 언급했던 FiLM과 Stochastic 방식으로 학습한 성능입니다. 보시면 주황색 line이 가장 성능이 높은 것을 볼 수 있는데, 구체적으로 OASIS 데이터셋에서의 SSHN을 보면 대부분의 rescaling factor에서 평균 0.89 이상의 성능을 보입니다. 이는 inference time에서 cost를 줄이면서도 accuracy를 희생할 필요가 없음을 시사합니다.

또, Fixed, Stochastic, FiLM 모델은 scale factor에 대해 일관성있는 성능을 보이지는 못하고 있는데요, 그에 반해 SSHN에 의해 예측된 네트워크 같은 경우 특정 rescale factor로 학습한 동일한 네트워크보다 일관성있게 더 정확한 것을 보입니다. 이는 SSHN 모델이 다른 접근 방식과 비교해봤을 때 rescale factor에 기반하여 weight를 잘 update하고 있기 때문이라고 해석해볼 수 있겠습니다.

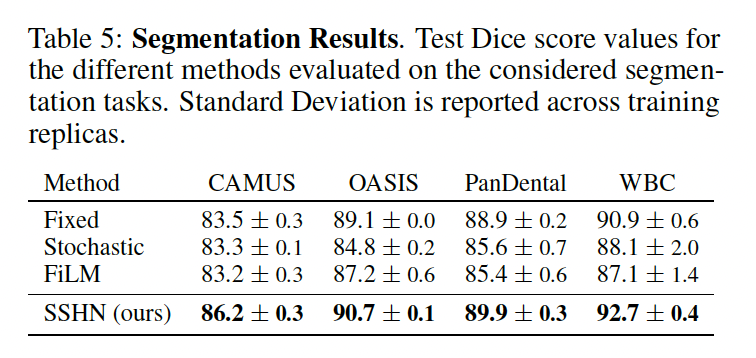
위 표는 방금 본 그래프를 정량적 수치로 표현한 표입니다. 결과를 보시면 모든 데이터셋에 대해 가장 높은 성능을 보이고 있습니다.

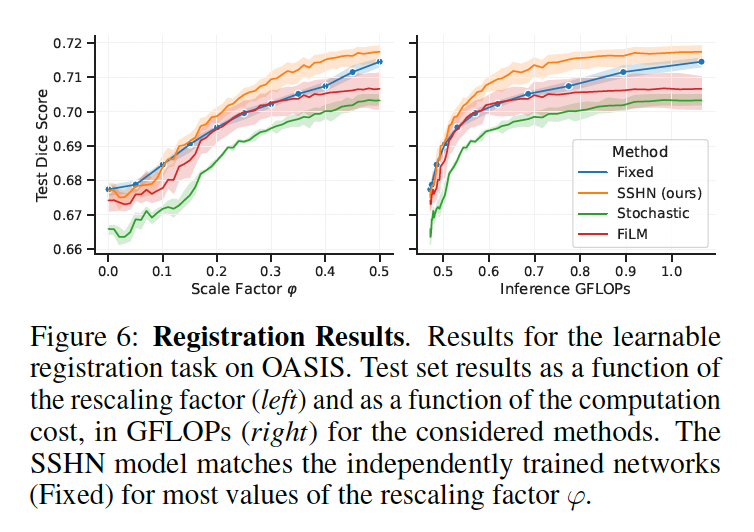
위 Fig6은 OASIS 데이터셋의 registration 결과를 보여주고 있습니다. 여기서도 SSHN 네트워크는 fixed된 , 즉 우리가 평소에 사용하는 일반적인 네트워크의 성능을 능가함을 보여줍니다. 반면에 stochastic이나 FiLM 방식을 사용할 경우 fixed보다 살짝 낮은 성능을 보이고 있습니다.

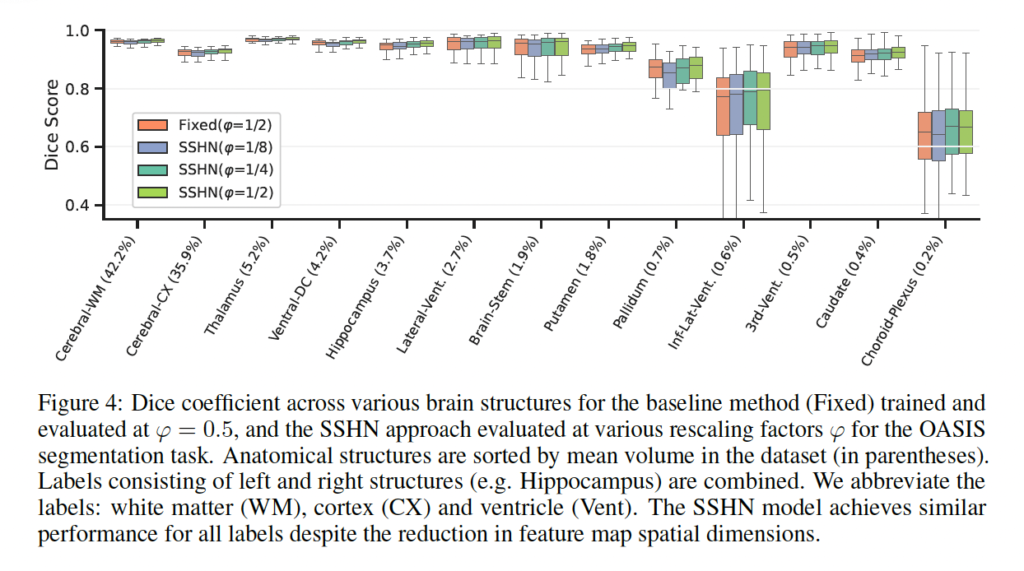
위 FIg4는 OASIS 데이터셋에 대해 다양한 rescaling factor가 이미지의 적은 label들에 대해 어떻게 반응하는지에 관한 실험입니다. 실험에서는 하이퍼네트어크 모델과 0.5로 rescaling factor를 고정한 모델에 대해 수행되었습니다. 그림에서 빨간색이 Fixed된 모델이고 나머지가 SSHN 모델입니다. 보시면, 제안된 하이퍼네트워크 모델이 라벨의 크기와 상관없이 모든 경우에서 비슷한 성능을 보여주었는데요,

이번 연구에서는 OASIS 데이터셋을 사용해 이미지의 작은 라벨들이 재조정 비율 변화에 어떻게 반응하는지 조사했습니다. 실험에서는 하이퍼네트워크 모델과 고정된 재조정 비율을 적용한 기존 모델을 비교했습니다. 이건 fixed된 모델을 사용할 때보다 후러씬 큰 rescale factor로 feature를 downsampling하더라도 segmentation 성능이 유지됨을 시사합니다. 즉, 하이퍼네트워크 모델이 다양한 크기의 물체를 일관되게 처리하는 능력이 있으며, 낮은해상도에서도 좋은 성능을 낸다는 장점을 갖고있다고 볼 수 있겠습니다. 이는 의료 이미지 분석에서 중요한 부분이겠죠.