[ICML 2022] Efficient Test-Time Model Adaptation without Forgetting

안녕하세요.
오늘 작성할 리뷰는 EATA 라고 불리는 TTA 분야의 논문입니다.

기존 TENT 방법론 대비 조금 더 효율성을 증대한, efficient 한 TTA 방법론입니다.
바로 리뷰 시작하겠습니다.

---

1. Introduction

TTA의 서론에 대해서는 이전 리뷰들에서 자주 설명드렸으므로 생략을 하도록 하겠습니다.

본 논문은 ICLR 2021년에 발표된 TENT 논문의 후속작입니다. (저자는 다릅니다)
TENT와 마찬가지로 Fully Test-Time Adaptation 분야의 논문입니다.

저자는 앞선 TTA 방법론들이 크게 2가지 문제점을 가진다고 언급합니다.

i) TTA 수행 시 모든 test sample들에 대해서backward 과정을 수행합니다. 하지만 TTA 분야 자제가 실시간성 및 application 관점을 주로 고려하는 만큼, 이렇게 모든 test sample에 대해 연산을 수행하는 것은 cost 가 많이 들고 비효율 적이라고 언급합니다.
ii) TTA는 기존 학습 domain과는 다른 새로운 domain 의 데이터가 등장했을 때 성공적으로 adaptation을 수행하기 위한 연구입니다. 즉 기존 in-distribution(ID) 데이터와는 다른 out-of-distribution(OOD) test sample에 대해 adaptation을 잘 수행하는 것이죠.
하지만 기존 연구들에선 모델이 OOD test sample에 대해서만 집중하여 모델 parameter를 update 하다 보니, 기존에 잘 가지고 있던 ID sample들에 대한 지식과 표현력을 잃어버리게 된다고 말합니다. 이를 전문 용어로 (catastrophic) forgetting 이라고 합니다.

---

저자들은 크게 이렇게 2가지 문제점을 정의하고, 이를 해결하기 위한 contribution을 아래와 같이 제시합니다.

우선 Model의 adaptation관점에서 모든 tseet sample이 도움이 되는 것은 아니라고 합니다. 너무 높은 entropy 값을 가지는 test sample은 noisy gradient를 초래해서 모델을 방해하는 요소로 작용하게 되므로 이에 대한 filtering 이 필요합니다. 따라서 reliable test sample과 non-redundatnt sample (noisy sample)을 구분하는 특정 기준(criterion)을 설계하게 됩니다. 구체적으로 이 criterion을 통해 filtering 되는 것은 i) 높은 entropy를 가지는 sample, ii) 매우 유사한 sample 입니다.

또한 ID(In Distribution) test sample에 대한 성능 및 지식을 유지하기 위해 Fisher regularizer를 설계하여 모델의 forgetting 을 해결하고자 합니다. 이는 모델 parameter의 가중치가 크게 변하지 않게 합니다.

2. Method

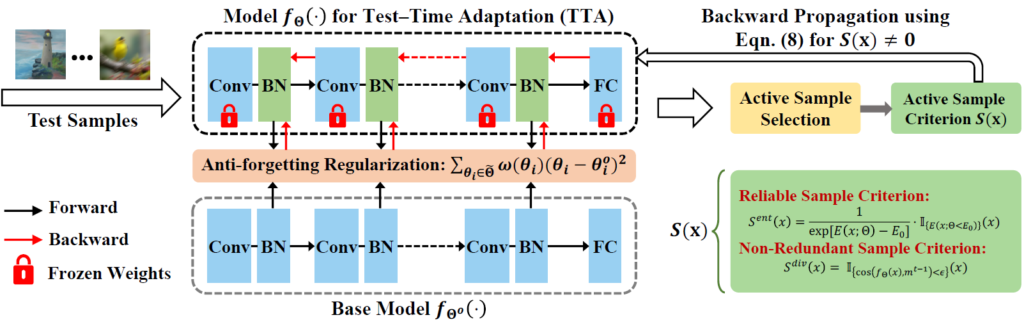
본 논문에서 제안하는 기법의 이름은 EATA (Efficient Anti-forgetting Test time Adaptation) 이며, 그 구조는 위와 같습니다. 그리고 이는 위에서 설명드렸듯 효율적인 TTA를 위해 도움이 되는 test sample만을 selection 하여 backward 과정을 수행하는 i) Sample-efficient entropy minimization 과, In-Distribution test sample 에 대한 knowledge forgetting 문제를 완화해주는 ii) Anti-forgetting weight regularization 로 구성되어 있습니다.

2.1. Sample Efficient Entropy Minimization

앞서 설명드렸듯 본 논문에서 설계한 EATA 에서는 모든 test sample 사용하여 backward 계산을 하는것이 아닌, i) reliable 하고 ii) non-redundant 한 test sample만을 골라서 더욱 효율적인 TTA 를 수행해야 한다고 주장합니다.

이를 위해 test sample을 선택하는 criterion인 S(x) 를 설계하게 됩니다. S(x)=0 가 되는 test sample x에 대해서는 backward 연산을 수행하지 않는 것을 의미합니다. S(x) 가 어떻게 동작하는지에 대해서는 아래에서 따로 말씀드리도록 하겠으며, 아래 수식은 S(x) 가 적용된 최종적인 objective fuction 입니다.
기존 TENT 에서 주장한 Entropy Minimization 수식에 S(x) 만 곱해진 형식입니다.
S(x)!=0 인 test sample x 에 대해 Entropy Mimization을 수행하겠다는 뜻입니다.

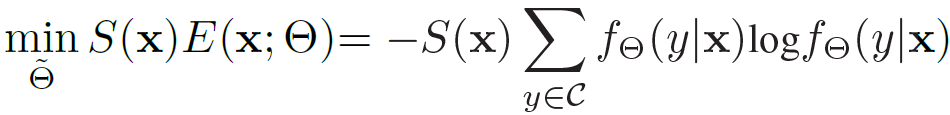
Reliable Sample Identification (Criterion)

저자들은 각 test sample 별로 최종적인 adaptation 성능에 기여하는 정도가 다를 것이라는 직관적인 생각을 했습니다. 이를 검증하기 위해 전체 test samples 중 entropy 순으로 일부 비율만을 선정해서 TTA를 수행하였고, 이에 따른 성능을 아래와 같은 그래프로 표현하였습니다.

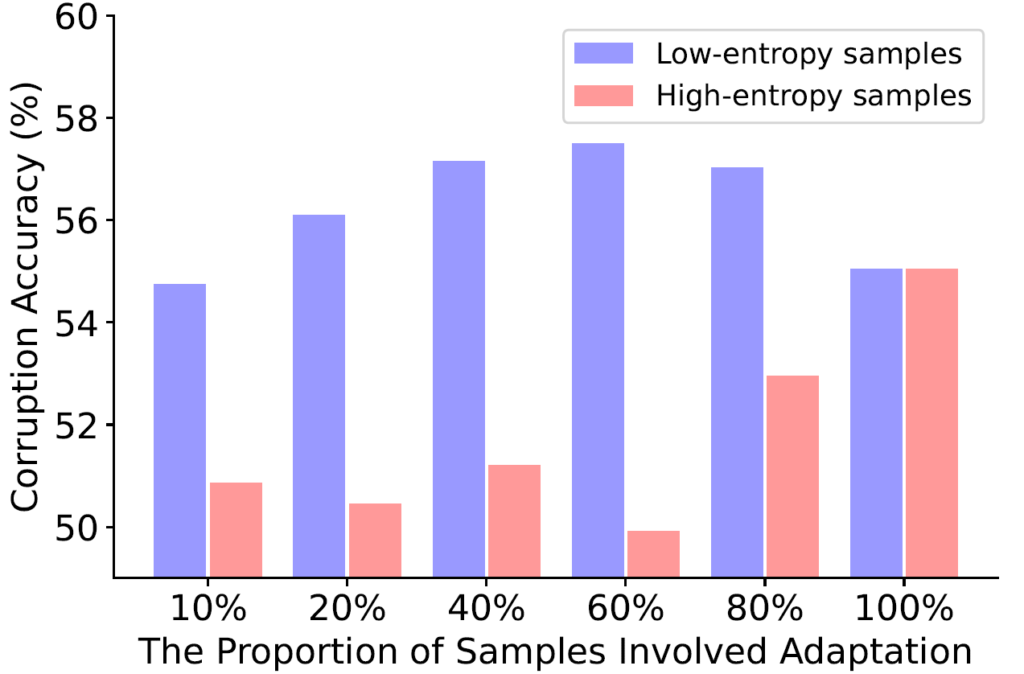
X 축의 %는 전체 test samples 중 adaptation에 관여한 샘플의 비율을 의미합니다. 100% 는 모든 test samples가 adaptation에 관여하였다는 것이고, 40%는 entropy 기준 하위 40% 만이 adaptation에 관여하였다는 것을 의미합니다. 그리고 y축은 이에 따른 성능을 의미합니다.

위 그래프를 통해 얻을 수 있는 결과는 2가지 입니다.
i) entropy 가 낮은 sample은 높은 sample 보다 adaptation 성능에 더 많은 기여를 한다.
ii) x축 %가 일정 수준 이상보다 커진 이후로 전체적인 성능이 하락하는 것으로 보아,
entropy가 높은 test sample은 오히려 adaptation 성능을 저하시킨다.

이와 같은 실험을 통해 저자들은 entropy 를 기반으로 각 test sample x 에 서로 다른 weight 를 주고자 하였고, 이를 나타내는 것이 아래 수식입니다.

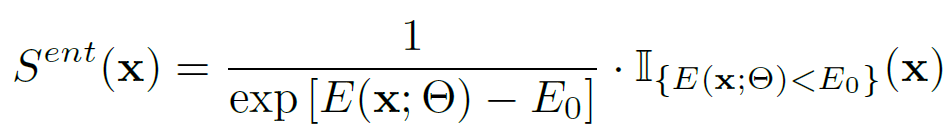
entropy E(x) 가 미리 정의된 threshold E_0 보다 작은 test sample x만을 indicator function을 통해 골라서 entropy 기반으로 유동적인 weight를 부여합니다. 이를 통해 entropy 가 낮은 test sample x 에 대해 더 높은 가중치를 할당할 수 있게 됩니다. 수식 및 컨셉적으로는 꽤나 간단합니다.

Non-redundant Sample Identification

위의 수식을 통해서 entropy가 높은 sample, 즉 unreliable한 test sample을 제외할 수는 있었습니다. 다만 나머지 test samples에 대한 redundancy 문제는 해결하지 못한다고 합니다.

예를 들어 entropy가 threshold E_0 보다 작은 매우 유사한 test sample x1과 x2에 대해, 두 sample을 모두 사용해서 backpropagation 과정을 수행하게 되면 효율성 측면에서 좋지 못하다고 합니다. x1과 x2 모두 비슷한 gradient를 생성하게 될 테니, TTA의 효율성을 향상시키기 위해서는 이러한 redundant test sample들을 판단해서 없애버릴 수 있는 criterion을 생성할 필요가 있다고 하네요.

사실 이를 위해 생각할 수 있는 가장 간단한 방법은 이전 time step때 마주한 모든 prediction을 저장해놓은 다음 현재 test sample로 부터 예측된 prediction과의 모든 유사도를 계산하면 됩니다. 하지만 점차적으로 누적될테니 효율성이 매우 떨어지죠.

이를 위해 EMA 기법을 활용해서 모델 adaptation에 관여한 모든 test sample들의 prediction 값을 update 해 나가서 ‘평균 모델 출력’ 을 생성해 나갑니다. 아래 수식을 통해 말이죠.

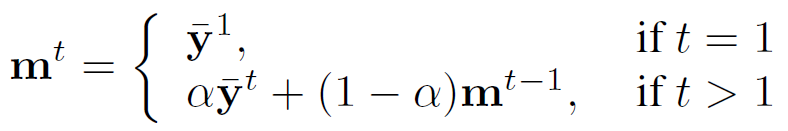
time step t 가 지남에 따라 m^t는 점차적으로 누적되면서 test sample 예측값들의 평균을 담게 됩니다.
그리고 이를 사용해서 아래의 새로운 criterion을 설계합니다.

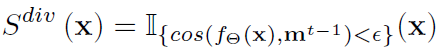
현재 time step t 에 들어온 test sample에 대한 예측과 m^{t-1} 과의 cosine 유사도를 구해서 미리 정의된 threshold 보다 작을 시 non-redundant한 test sample 이라고 판별하여 최적화 과정에 반영하게 됩니다.

그리고 앞서 entropy 기반으로 설계한 criterion 과 합쳐서 최종적인 criterion 을 구성하게 됩니다.

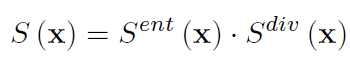
다시 정리하자면, efficient한 TTA를 위해 모든 test sample이 TTA에 반영되는 것이 아니라 일정 criterion을 기준으로 사용되게 됩니다. 그리고 이 criterion은 i) 높은 entropy를 가지는 test sample은 제외하고, 나머지들은 entropy에 반비례하도록 weight가 부여되며, ii) similarity가 높은 redundant test sample은 제외하고 adaptation에 반영되게 됩니다.

---

2.2. Anti-Forgetting with Fisher Regularization

또한 두번째로는 In-Distribution (이하 ID) 에 대한 knowledge를 망각하는 catastrophic forgetting 문제를 해결하기 위한 정규화 기법을 설계합니다.

이를 위해 아래 Regularizer R을 설계하게 됩니다. 그리고 이는 중요한 model parameter가 TTA 수행 과정 속에서 너무 많이 변경되는 것을 방지해 준다고 합니다.

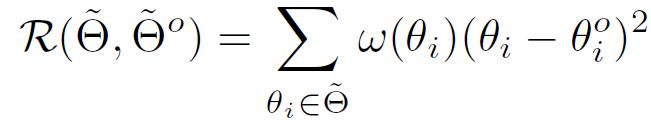
\tilde{\Theta}는 update가 진행되는 모델의 parameter를, \tilde{\Theta}^O 는 기존 원본 모델의 parameter를 의미합니다. 그리고 w(\theta_i)는 각 parameter 별 중요도를 나타내는 weight 수치이며, 이는 Fisher information matrix를 통해 계산된다고 합니다. 이에 대해서는 완벽하게 이해를 못하였지만, 아래 단락에서 따로 설명드리겠습니다.

어쨌든 이러한 제안 사항들을 통해 본 논문에서 사용하는 최종 objective function은 아래와 같습니다.

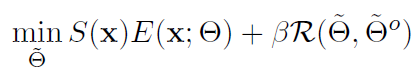
Measurement of Weight Importance w(\theta_i)

위 Regularization term 속의 w(\theta_i) 를 어떤식으로 계산하는지를 설명하기 위한 단락입니다.

저자들은 기존 TTA 기법에서 forgetting 현상이 발생하는 이유에 대해 OOD samples에 대해서만 맞추어 가다 보니 기존 ID samples 에 대한 정보를 잃어버리기 때문이라고 합니다. 그래서 이를 해결하고자 model parameter 가 TTA 과정 속에서 너무 많이 변경되는 것을 방지하고자 하였고, 이를 위해 Fisher information matrix 라는 개념을 가지고 와서 기법을 설계하였습니다.

Fisher information 계산을 위해서는 labeled ID training samples 를 사용해야 합니다. 하지만 TTA의 특성 상 학습 데이터에 접근할 수 없고, test samples 에 대해서도 gt가 존재하지 않습니다.
그리하여 이에 대한 대안책으로 unlabeled test samples 중 일부분을 샘플링하여 dataset x_q 를 구성합니다. 그리고 TTA가 수행되는 모델인 f_{\Theta} 를 통해 hare pseudo label \hat{y}_q 를 예측해 냅니다. 최종적으로 아래 수식을 통해 weight 를 계산할 수 있게 됩니다. 앞서 구한 hare pseudo label \hat{y}_q 와 base model f_{\Theta}^O 의 예측 사이의 cross entropy loss를 통해서 말이죠. 아래 수식을 통해 구해진 weight 값은 TTA 수행 전 한번 쫙 계산해두고 이후엔 fix 시켜서 사용합니다. 전처리 느낌으로 미리 계산해두는겁니다.

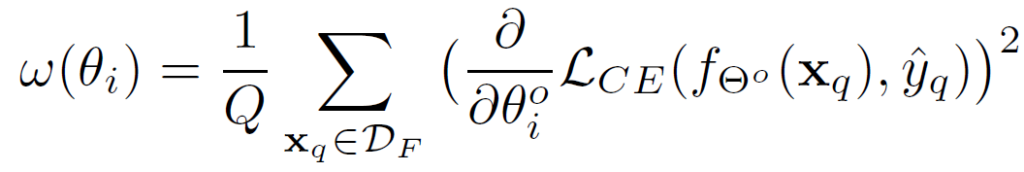
3. Experiment

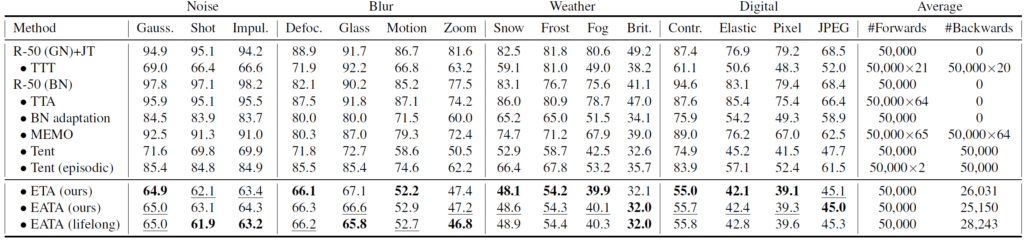
위 실험은 ImageNet->ImageNet-C 로의 TTA 실험 결과이며, 표기된 성능은 error(%) 입니다. 또한 위 table에서 EATA 는 본 논문의 최종 결과를 의미하며, ETA는 2.2절에서 설명드린 Fisher Regularization 기법을 제외하였을때의 성능입니다.

또한 위 table에 (lifelong) 이라고 하는 표기가 있을겁니다. 이는 TTA 가 수행이 되는 과정 속에서 model의 parameter를 초기 상태로 되돌리지 않겠다는 걸 의미합니다. 최근 연구들은 continual 한 domain shift 상황을 고려하기 때문에 TTA 수행 과정에서 당연히 model의 parameter를 초기 상태로 되돌리지 않습니다.
하지만 TENT, 그리고 본 논문에서 제안하는 EATA는 연속적인 (continual) domain shift 상황은 고려하지 않기 때문에 기본적으로 새로운 domain 으로 변화할 때 model의 parameter를 초기 상태로 되돌리게 됩니다.

즉 (lifelong) 의 의미는 좀 더 실용적인 TTA 라고 볼 수 있으며, continual 한 domain shift 상황에 대해 평가하기 위한 세팅이라고 보시면 됩니다.

위 table에서 ETA(ours) 와 EATA(ours) 의 차이는 forgetting 방지를 위한 Fisher Regularization 기법의 유무입니다. 사실 전체적인 성능으로 봤을 땐 크게 차이가 없어 보이네요. 그리고 EATA(lifelong) 의 경우에는 사실 TTA가 수행됨에 따라 후반부로 갈 수록 성능 하락폭이 꽤나 클 줄 알았는데 기존과 유사한 것을 볼 수 있습니다. forgetting 방지를 위한 Fisher Regularization 기법이 ID samples의 지식을 잘 보존해서 continual 한 상황에 도움이 된 것으로 보여집니다.

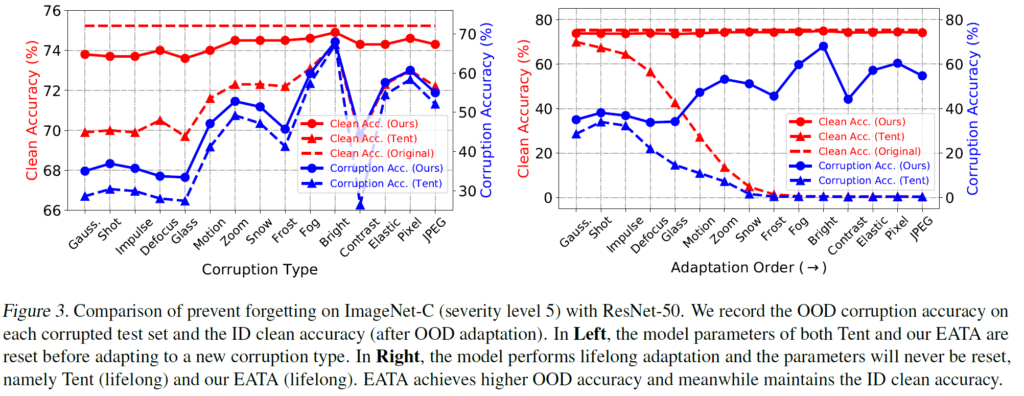
위 실험은 ID 와 OOD 각각의 accuracy 성능을 살펴보기 위해 진행한 실험입니다. EATA 에서는 기존 방법론의 문제점으로 ‘OOD 로의 adaptation만을 고려하기 때문에 기존에 가지고 있던 ID 에 대한 지식을 forgetting 한다’ 라고 언급했습니다. EATA 에서 이러한 forgetting 문제를 잘 해결했는지를 보여주기 위한 실험인것이죠.

우선 좌측 그래프는 lifelong을 고려하지 않은 실험 결과입니다. 즉 domain 상황이 변화할 때 마다 다시 model parameter를 초기로 변경하는 것이죠. 반면 우측 결과는 lifelong 을 고려한 것입니다. x축을 따라 adaptation이 진행되는 과정에서 model parameter가 초기로 돌아가지 않고, 끊임없이 TTA로 update 해 나가는 것입니다.
그리고 빨간색 그래프는 source data로 평가한, 즉 In-Distribution(ID) 의 성능이구요, 파랑색 그래프는 corruption이 부여된 상황에서의 Out-Of-Distribution(OOD) 의 성능입니다.

좌측도 좌측이지만 특히 우측의 결과가 인상적입니다. TTA 후반부로 갈 수록 tent 에서는 성능 accuracyy가 0으로 낮아지는 것을 볼 수 있습니다. 물론 TENT 가 이런 연속적인 domain 변화 상황을 타겟으로 한 방법론이 아니긴 합니다만, 아무튼 이 실험을 통해 EATA가 초기 ID data에 대한 정보/지식을 forgetting 하지 않고 잘 유지하고 있는 것을 보여주고 있네요.

---

네 오늘은 EATA 라고 하는 TTA 논문 리뷰를 해 보았습니다.
효율적인 TTA를 위해 특정 criterion을 설계해서 sample 을 selection 하는 기법, 그리고 forgetting 방지를 위한 regularizer 설계. 최근 2023~2024 논문들에서는 흔히 발견할 수 있는 컨셉이긴 합니다만, 당시 상황에서 꽤나 참신한 문제정의와 직관적인 해결 방안을 잘 제안한 논문인 것 같습니다.

리뷰 마치도록 하겠습니다. 감사합니다.