안녕하세요,

이번에 리뷰할 논문은 오래간만에 instance-level에서의 6D pose estimation 방법론입니다.

선행 연구로 제안된 ZebraPose의 문제점들을 해결하기 위해 제안된 방법론으로, binary encoding을 통해 pose를 추정하는 신박한 방법론입니다.

작년에 본격적으로 여러가지 6D 방법론에 대한 환경 세팅을 하면서 ZebraPose도 세팅을 해봤는데, 결론적으로는 환경 세팅에 2-3주 정도 소요하고 포기했었던 기억이 나네요..

리뷰 시작하겠습니다.

Introduction

물체의 6D pose를 추정하는 것은 3D 컴퓨터 비전의 근본적인 문제라고 볼 수 있습니다. pose 추정은 증강 현실, 파지, 자율 주행 등 수 많은 어플리케이션에서 적용할 수 있습니다. 이러한 중요성을 띄고 있음에도 불구하고 물체의 균일한 텍스처를 가지는 경우, occlusion이 심한 경우에 대해 여전히 pose 추정을 하는 것은 어려운 문제로 남아있습니다.

이번 논문에서는 RGB-D를 입력으로 받아 세부적인 정보들을 최대한 활용하여 물체의 정확한 pose를 예측하는 것을 목표로 합니다. dense한 2D-3D correspondence를 생성하는 선행 연구인 ZeroPose를 기반으로 하여 입력으로 들어가는 depth 정보를 통해 물체의 3D CAD 모델 간의 dense한 3D-3D correspondence를 효율적으로 예측하는 HiPose를 제안합니다. ZebraPose와 달리, 이상값을 반복적으로 제거하여 coarse-to-fine 과정을 거쳐 해당 특성을 더 잘 활용하는 방식으로 encoding을 처리하도록 설계하였습니다.

이번 논문의 contribution은 다음과 같습니다.

• 계층적 binary surface encoding을 통해 3D-3D correspondence에 대한 align을 맞추는 것에 초점을 맞추어 RGB-D에 대한 두 가지 모달리티를 전부 활용하는 방법론인 HiPose 제안
• coarse-to-fine surface에 대한 outlier를 제거함으로써 기존의 RANSAC이 필요없는 hierarchical correspondence pruning 제안
• LM-O, YCB-V, T-LESS에서 SOTA 달성

Method

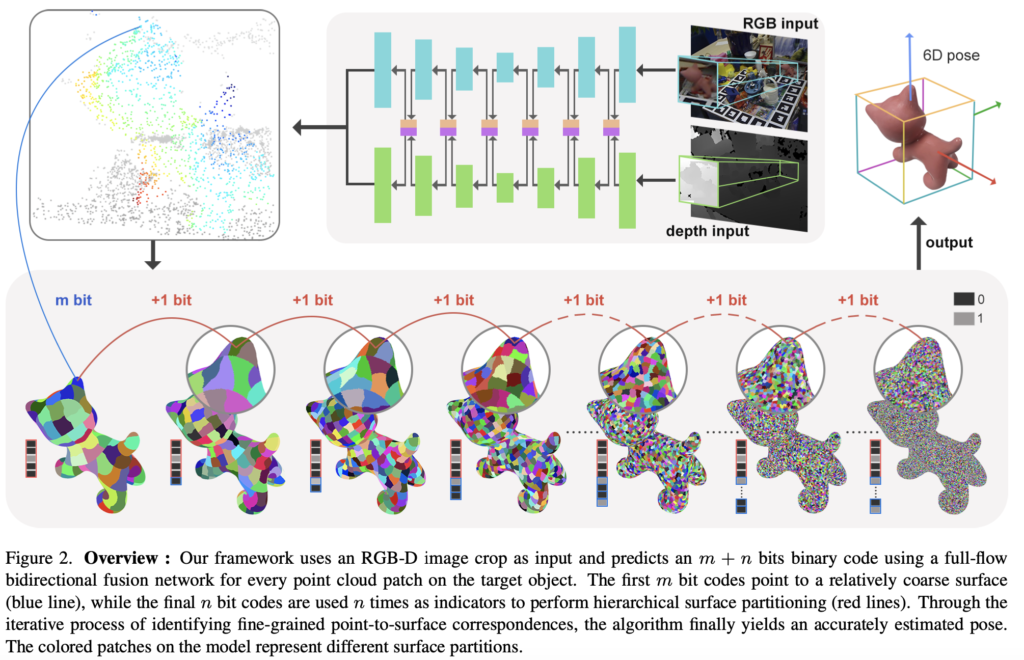
이번 HiPose는 이전에 제안된 ZebraPose의 문제점을 개선하여 좀 더 고도화 된 방법론입니다. 어떤 문제들을 다루는지 자세하게 살펴보도록 하겠습니다.

ZebraPose에서는 RGB 이미지로부터 pose를 추정하기 위해 binary encoding을 사용했었습니다. 이미지 내에 존재하는 물체를 먼저 검출하여 얻은 바운딩 박스 내의 모든 픽셀 \mathbf p_{u,v}에 대해 d 비트 만큼의 binary code를 추정하도록 학습을 시킴으로써 해당 픽셀과 3D CAD 모델의 vertex \mathbf v_{i} 간의 2D-3D correspondence를 생성할 수 있었는데요. 이를 통해 물체에 대한 pose를 추정하기 위해 RANSAC+EPnP(최근 제안된 학습 기반의 PnP 알고리즘)을 적용하면 최종적으로 저희가 원하는 6D pose 값들을 얻을 수 있었습니다.

하지만, 저자는 ZeroPose에 대한 3가지 문제점들에 대해 언급을 하는데요.

1. 최종 pose에 대한 refinement 과정을 제외하고 depth 정보를 활용하는 과정이 없음
2. encoding된 surface를 예측하는 어떤 계층적 특성에 대해 명시적으로 활용하는 것이 없음
3. 예측된 surface code의 confidence score를 활용하지 않고 0, 1로 나타내는 bit 값으로 바꾸는 행위를 통해 confidence에 대한 정보를 모두 소실시킴

Point-to-Surface Correspondence

첫 번째 문제점을 개선하기 위해 제안된 HiPose에서는 ZebraPose와 동일하게 RGB-D를 입력으로 받아 각각에 대한 모달리티에서 특징을 추출하여 ZebraPose와 다르게 3D-3D correspondence를 예측하도록 설계되었는데요. 그림(2)를 보시면 RGB와 depth 각각에 대해서 검출된 RoI 영역에 대한 입력을 먼저 받습니다. 이후 FFB6D와 동일하게 양방향 융합 구조로 만들기 위해 2개의 branch로 나아가는 것을 확인할 수 있습니다. 각 3D 포인트 \mathbf P에 대해 모델은 binary code \mathbf {\hat c}를 예측하도록 학습이 진행됩니다. 해당 binary code는 그럼 어떤 포인트 클라우드와 3D CAD 모델 간 3D-3D correspondence를 나타내는 것으로도 볼 수 있겠습니다. 해당 correspondence를 이용하여 Kabsch 알고리즘을 적용하여 pose 추정을 진행하였다고 합니다.

두 번째 문제점은 계층적 특성을 활용하는 것이 없다는 것이었는데요. 이는 기존의 ZebraPose에서 coarse-to-fine 과정에서 해당 특성을 고려하지 않고 적용이 되었으므로, 저자는 여기서 point-to-surface라는 새로운 방법을 제안하는데, 좀 더 풀어보면 ZebraPose에서는 마지막 비트에 대한 높은 불확실성도 포함하는 d비트 전체를 사용하는 것이 아니라 해당 binary code를 두 개(m, n 비트; d=m+n)로 나누는 것을 제안하였다고 보시면 되겠습니다.

(여기서 사용되는 binary encoding은 encoding되는 bit 수에 따라 물체의 surface에 대해 manifold로 나타낼 수 있습니다. 참고로 manifold는 3D CAD 모델의 mesh에는 수 많은 vertex들로 이루어져있는데요. 전체 mesh 중 단일 vertex를 나타낸다고 보시면 되겠습니다.)

encoding의 첫 번째 m비트는 depth로부터 얻은 포인트 클라우드와 3D CAD 모델의 surface \mathcal S_{m}에 대한 3D-3D correspondence를 생성하는 역할을 합니다. 이는 \mathcal S_{m}에 대해 중심점(전체 3D CAD 모델에 대한)을 계산하고 3D 포인트를 사용하여 생성하게 됩니다. 이러한 대응 관계로부터 coarse한 pose를 얻을 수 있겠네요. 이러한 coarse pose를 fine pose로 refinement하는 과정을 m+1비트부터 m+n비트까지 반복하여 진행합니다. 그림(2)의 아래 행 그림을 보시면 refinement를 반복하는 과정에서 interest surface의 크기가 점점 감소하는 것을 볼 수 있습니다. 이러한 반복을 통해 pose 정확도 상승 뿐만 아니라, outlier까지 제거할 수 있는 효과도 있었다고 하네요.

Hierarchical Binary Code Decoding

세 번째 문제는 confidence score 값을 0, 1 값으로 binary code 형태로 사용하였다는 것인데요. 이렇게 사용할 경우는 예측된 추정된 code(confidence score가 존재)에 있는 정보를 버리는 행위로, 이후 RANSAC-PnP 알고리즘에 태우면 성능이 크게 좌우될 정도라고 하니 중요한 역할을 할 것 같습니다.

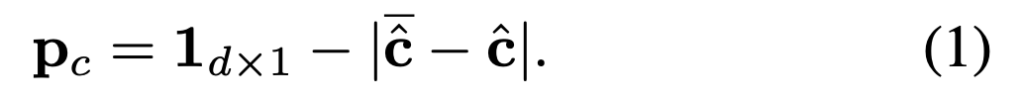
따라서, 저자는 direct 버전(confidence 값 존재)과 quantize 버전(기존 binary code)을 둘다 사용하여 probability/confidence를 식(1)과 같이 계산하여 동시에 잡기 위한 방법을 제안합니다. direct code \mathbf {\bar {\hat c}}와, quantize code \mathbf {{\hat c}}에 대한 잔차의 절댓값을 취한 후 전체 확률 1에서 값을 빼주어 특정 확률 값을 얻을 수 있겠네요. 이러한 확률 정보를 활용하여 여러 번 반복 수행을 함으로써 우수한 성능까지 얻을 수 있었다고 합니다. 해당 과정을 binary code decoding 과정이라 하며, 이러한 decoding 과정은 initial surface selection과 sub-surface partitioning으로 확장되어 사용됩니다.

Initial surface selection

그림(2)를 보시면 포인트 클라우드에서 특정 점을 파란선으로 CAD 모델의 특정 surface와 이어진 것을 확인 할 수 있는데요. 해당 과정이 initial surface selection 과정입니다. 이러한 복잡한 surface를 representation하는 bit 사용하는 것은 모델이 학습하기 적절하지는 않아보입니다. 저자는 이러한 문제를 해결하기 위해 학습에 용이하도록 적절한 surface를 선택하거나, binary encoding을 적절하게 나누는 m을 선택하는 것을 제안합니다. 앞서 식(1)을 통해 얻은 \mathbf P_{c}를 기반으로 하여 특정 threshold 값보다 높은 애들만 담은 code 중 가장 마지막 비트 j를 신뢰 비트(trust bit)로 정의합니다. notation은 \mathbf P_{c}^{j}으로 표현하네요. 해당 신뢰 비트를 이용하여 sub-surface의 최대 크기를 제한하는 m의 최소값으로 m_{default}를 설정하여 최종적인 m=\max(j, m_{default})를 얻어 pose 추정을 반복하여 진행합니다. 이를 통해 pose 추정 과정에 정확도 뿐만 아니라 계산 복잡도까지 잡을 수 있었다고 하네요.

Sub-surface Partitioning

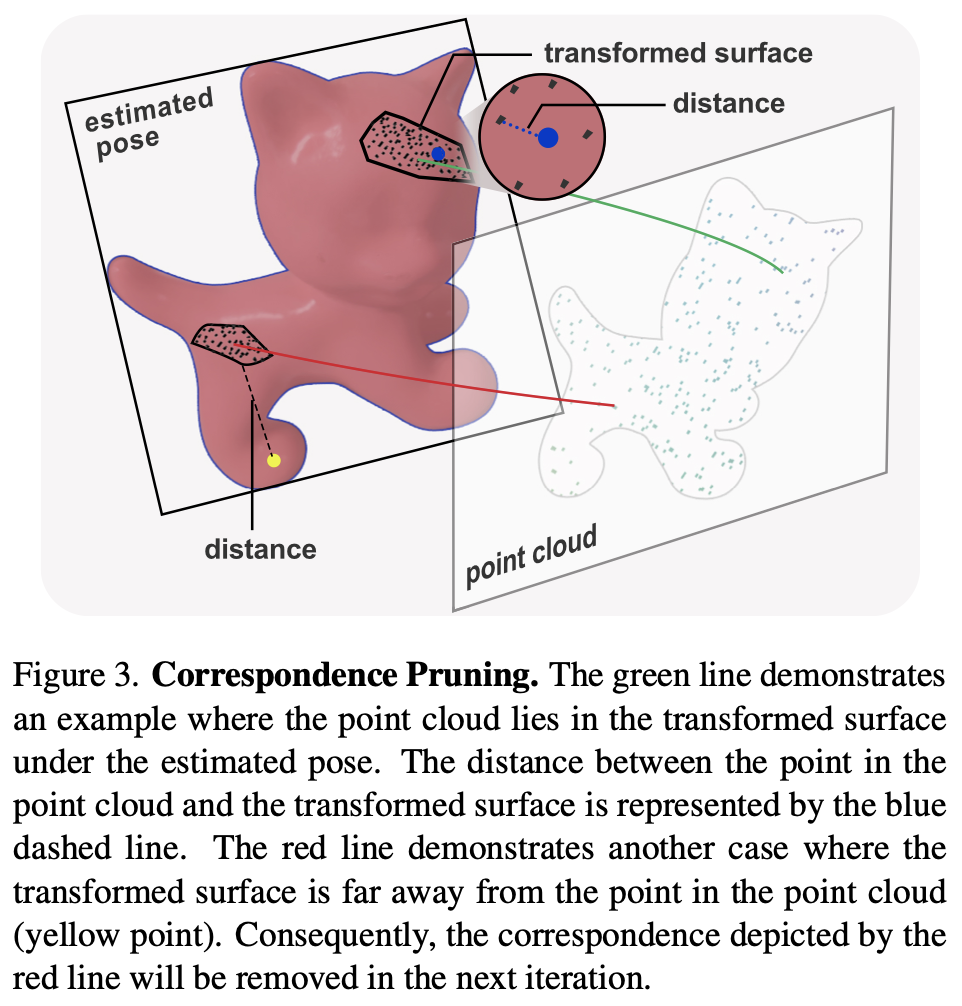
다시 그림(2)의 빨간선은 sub-surface에 대한 분할 과정을 나타내고 있습니다. 반복하는 과정 중에 surface가 줄어들면 대응 관계에 대해 학습하기가 점점 어려워 질 것이고 이는 곧 confidence score 마저 떨어뜨리게 될텐데요. 저자는 이러한 문제를 해결하기 위해 세분화된 반복 과정을 진행하면서 세분화된 surface에 대해 pose 추정을 수행하기 전에 hierarchical correspondence pruning 과정을 진행합니다.

이전에 진행한 point-to-surface correspondence에 대한 과정을 통해 추정된 code의 m비트부터 시작해서 해당 surface S_{m}과 모든 vertex \mathbf v_{i}에 대한 중심값 \mathbf g_{m}을 계산할 수 있습니다.

sub-surface에 대한 분할 및 pose 추정은 m+1(시작)비트부터 d(끝)비트까지 n회 반복됩니다. 이러한 반복 과정을 거치면서 포인트 클라우드에서 마스크 된 영역에 대해 해당 sub-surface와 대응되는 좌표에 대해 중심값을 계산하고 Kabsch 알고리즘을 통해 pose를 추정하고 아래의 식(2)와 같이 거리 값을 계산하여 inlier를 선택하게 되는데요.

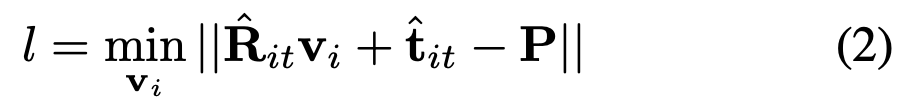
(it+1) 번째 반복에서는 이전에 구한 pose에서 점 \mathbf P와 변환이 적용된 sub-surface \mathbf {S^{\prime}} 사이의 모든 correspondence에 대한 거리를 계산하여 이를 threshold로 사용함으로써 inlier/outlier를 구분합니다.

그림(3)은 위의 내용을 시각적으로 나타내고 있습니다. 따라서, 식(2)와 같이 포인트 클라우드 내의 점 \mathbf P와 변환이 적용된 surface 사이의 최소 거리를 정의할 수 있습니다.

Experiments

Implementation details

기존의 FFB6D 양방향 융합 모듈을 그대로 사용하였으며, 추가적인 수정 사항을 적용하여 HiPose를 구성하였다고 합니다. 저자가 수정 및 추가한 부분은 기존 3개의 출력 헤드를 visible mask가 포함된 단일 헤드로만 대체하고, 랜덤으로 선택된 모든 점에 대해 d 비트의 binary code를 사용하도록 설계합니다. 이렇게 visible mask와 binary code 각각 L1 loss를 사용하여 학습을 진행하였다고 합니다. 이때 binary code 예측 같은 경우, 예측된 visible mask 내의 포인트에 대해서만 loss를 계산합니다.

Datasets

LM-O, YCB-V, T-LESS

Metrics

ADD, AUC

Ablation Studies

Effectiveness of Correspondence Punning

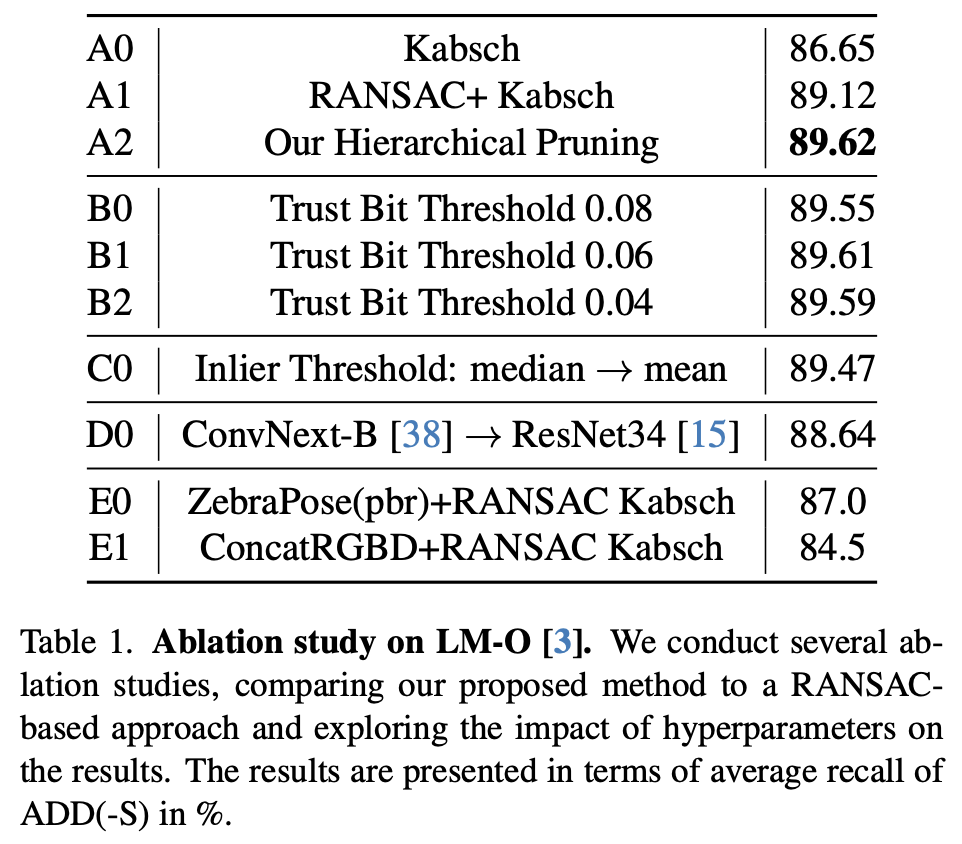
표(1)은 저자가 제안한 correspondence pruning의 효과를 보여주고 있습니다. A0~A2를 보면 저자가 제안한 binary encoding의 효율성에 대해 강조할 수 있는 표로 보이네요.

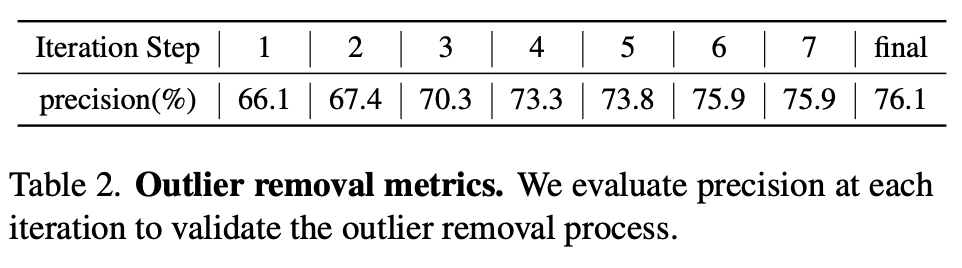
또한 표(2)는 각 반복마다 outlier 제거에 대한 정밀도를 측정한 표입니다. 추정 좌표와 GT 좌표 사이의 거리가 10mm 미만일 경우 옳은 샘플로 정의합니다. 반복 과정을 통해 점진적으로 outlier들이 제거 되면서 정밀도가 증가하는 것을 확인할 수 있습니다.

Influence of Default Initial Bit

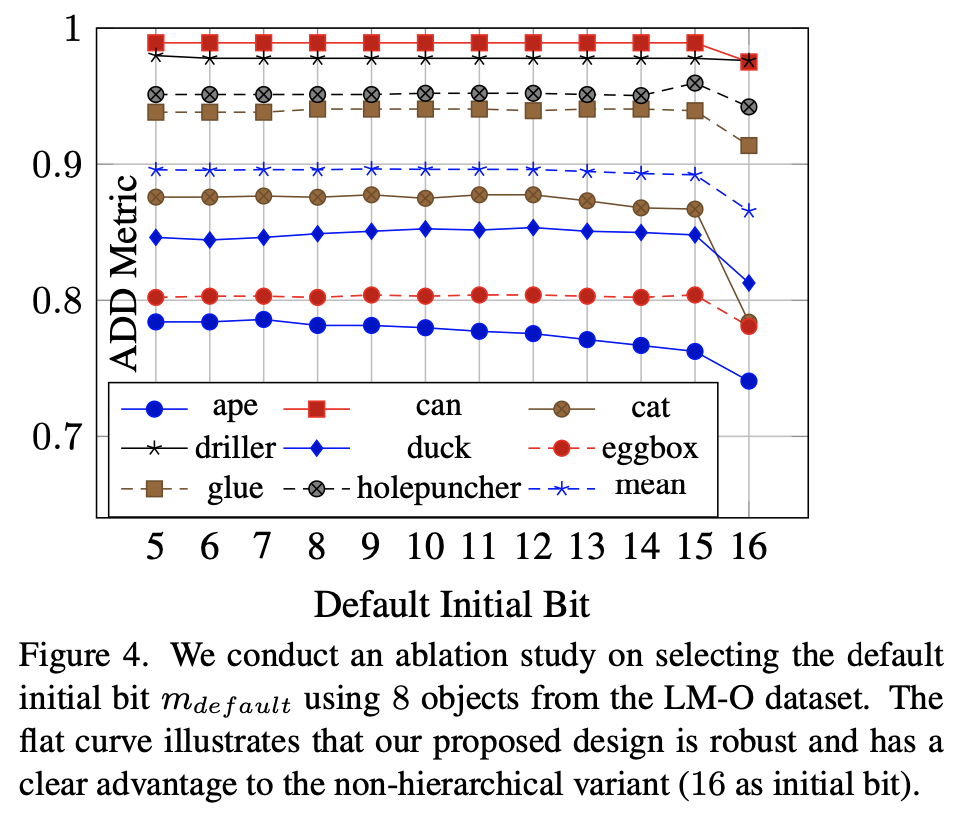
작은 초기 비트를 사용하는 것은 상대적으로 coarse한 surface correspondence와 매칭을 시킨다는 의미를 갖게 되는데요. 하지만 저자가 제안한 신뢰 비트를 사용하여 초기 surface에 대한 선택이 가능하게 되어 각 vertex가 개별적으로 고려되어 가장 신뢰할 수 있는 초기 비트에 대응이 되도록 합니다. 이에 대한 증명을 하는 그림(4)을 보면, 5비트에서 11비트까지는 초기 비트 선택에 대해 강인한 모습을 보이지만 12번째 비트부터 시작하면 ape에서 성능이 떨어지기 시작하는 모습을 확인할 수 있습니다. 해당 실험을 통해 9~11번째 비트를 초기 비트로 사용하면 좋은 결과를 얻을 수 있다는 것을 알 수 있었다고 하며, 정확도와 계산 효율성을 모두 고려하여 10번째 비트를 사용하여 리포팅을 했다고 하네요.

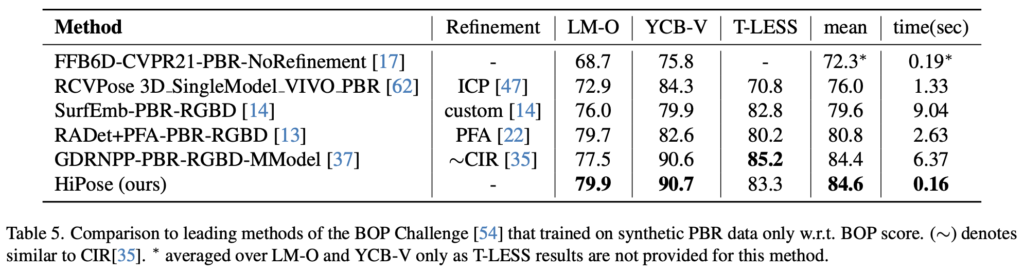
마지막으로 BOP benchmark 데이터셋들에 대해 결과를 보여주는 표(5)입니다. 해당 표에는 시간이 주로 많이 사용되는 refinement 과정에 의존하는 방법론도 있습니다. HiPose는 refinement 과정 없이 바로 추정을 하여도 기존의 방법론들에 비해 우세한 성능을 보여주고 있습니다. GDRNPP 같은 경우 HiPose와 비슷한 성능을 보이지만, refinement 과정을 거친 GDRNPP 보다 HiPose가 40배 더 빠른 모습을 보여주고 있으며 이러한 결과를 통해 HiPose는 정확도뿐만 아니라 계산적으로 효율적으로 수행하고 있다는 것을 증명합니다.

Conclusion

이번에는 RGB-D 기반의 방법론으로 제안된 HiPose에 대해 살펴보았습니다. 선행 연구로 제안된 ZebraPose를 개선한 모델로 예측된 code에 대한 confidence를 고려하여 outlier를 제거할 수 있었습니다. 또한 시간이 많이 걸리는 correspondence pruning을 통해 효율적인 연산까지 수행할 수 있었습니다.

이상으로 이번 리뷰 마치도록 하겠습니다.

감사합니다.