[ICLR 2022] Understanding Dimensional Collapse In Contrastive Self-Supervised Learning

안녕하세요. 허재연입니다. 이번 주차 세미나에서 Self-Supervised Learning의 collapse 문제에 대한 언급이 있었는데요, 이에 관심이 생겨 관련 논문을 읽어보게 되었습니다. 제목에서 알 수 있다시피 contrastive learning의 dimensional collapse를 다룬 논문입니다. 막연히 contrastive learning이 dimensional collapse 문제를 갖고 있다는 것은 알고 있었는데 이 논문을 읽으며 어느 정도 이해도를 높일 수 있었습니다. 하지만 수학적인 배경을 상당히 요구해서 읽는데 어려움이 많았습니다.. 2022년 ICLR에 게재되었던 논문으로, 얀 르쿤 등 페이스북 연구진들이 발표한 논문입니다. 바로 리뷰 시작하도록 하겠습니다.

Abstract

Self-Supervised visual representation learning은 사람이 annotation한 정답 값 없이 좋은 representation을 학습하는 것을 목표로 합니다. 이러한 여러 self-supervised learning(SSL) 방법 중 Joint embedding 접근법은 동일한 이미지 데이터를 다르게 증강시킨 것으로부터 얻은 임베딩 벡터 간 유사도를 높이는 방법을 기반으로 합니다. 하지만 해당 방법은 모든 임베딩 벡터가 constant vector로 수렴하는 collapse 문제를 가지고 있습니다. 이를 해결하기 위한 다양한 방법이 제안되었는데, 그 중 하나인 contrastive learning 방법은 negative pair를 사용하여 collapse 를 방지하였습니다. non-contrastive learning 방법들은 좀 더 작은 collapse 문제인 dimensional collapse 문제(임베딩 벡터가 모든 임베딩 공간을 활용하지 못하고 특정한 저차원 부분공간으로 span되는 현상)를 갖고 있는것이 밝혀져 있는데, 본 논문에서 저자들은 dimensional collapse가 contrastive learning 방법에서도 발생함을 밝히고, contrastive learning에서 dimensional collapse를 유발하는 요소들을 분석합니다. 또한 trainable projector에 의존하지 않고 representation space를 직접 최적화하는 DirectCLR이라는 새로운 contrastive learning 방법을 제안합니다.

Introduction

컴퓨터 비전 태스크를 수행하기 위해 딥러닝 모델을 훈련시키기 위해서는 많은 양의 데이터가 필요합니다. 하지만 데이터를 수집하고 라벨링하는데는 너무 많은 시간과 비용이 필요하기 때문에, 라벨이 없는 이미지 데이터만으로 모델에게 좋은 pretrained weight를 제공하기 위한 self-supervised learning 방법 연구가 이루어지고 있습니다. 이러한 방법들은 보통 visual representation learning이나 self-supervised/unsupervised learning 이라 부르고, 다양한 방법으로 모델을 사전학습 시킬 수 있는 방법론들이 제안되어 이제는 supervised learning 방법으로 사전학습 한 것에 뒤떨어지지 않는 표현력을 학습시킬 수 있게 되었습니다.

일부 기존 SSL 방법들은 동일한 이미지에 다른 증강을 가해 두 개의 view를 만들고, encoder(ResNet과 같은 비전 백본)를 거쳐 나온 이들의 임베딩 벡터 간 유사도를 높이는 방향으로 진행되어 데이터 증강에 불변하는 표현을 학습하는 것을 목표로 했습니다. 하지만 이런 방식으로 훈련을 진행하게 되면 모델이 모든 input값을 동일한 constant vector에 매핑하는 collapsing problem이 발생하게 되어 이를 해결하기 위한 다양한 방법이 제안되었습니다. 대표적인 방법론들이 SimCLR나 MoCo와 같은 contrastive learning 방법인데, 이 방법론들은 동일한 데이터의 서로 다른 view(positive pair)만 활용하는 것이 아니라 다른 데이터를 묶은 negative pair를 정의하여 손실함수에서 positive pair와 negative pair가 다르게 처리되도록(positive pair 임베딩 벡터의 유사도를 높아지고, negative pair 임베딩 벡터의 유사도는 낮아지도록) 하였습니다. contrastive learning 이외에도 BYOL, SimSiam과 같은 non-contrastive learning 방법론들은 negative pair를 사용하지 않고 collapse를 방지하기 위해 stop-gradient를 사용하였고, DeepCluster는 추가적인 클러스터링을, Barlow twins는 두 branch 간 중복되는 정보를 최소화합니다.

이러한 Self-Supervised Learning 방법들은 모든 representation 벡터들이 single point로 모이는 완전한 collapse를 막는데는 성공했지만, 몇몇 non-contrastive learning 방법론들이 특정 차원을 따라 붕괴되는 것이 실험적으로 관찰되었다고 합니다. 임베딩 벡터들이 저차원 subspace로만 span되는 이러한 현상을 dimensional collapse라고 부릅니다(충분히 많은 차원을 사용하지 않기 때문에 표현력이 제한된다고 받아들이시면 될 것 같습니다).

손실함수 측면에서 positive pair와 negative pair를 명시적으로 사용하는 contrastive learning의 경우, 직관적으로 생각하면 negative pair의 상호 간 반발 효과가 있기 때문에 이러한 dimensional collapse를 방지하고 가용한 모든 차원을 사용하게 될 것으로 생각됩니다. 하지만 이러한 직관과는 다르게 contrastive learning 학습 방법 또한 dimensional collapse 문제를 일으킨다는 것이 관찰되었다고 합니다. 저자들은 dimensional collapse를 유발하는 2개의 메커니즘에 대해서 언급하는데, 다음과 같습니다 :

1. 데이터 자체 분포에서의 분산보다 데이터 증강으로 인한 분산이 커짐에 따라 weight가 붕괴된다. 너무 강력한 데이터 증강으로 인해 생기는 데이터 분포의 분산이 서로 다른 데이터 간 데이터 분포 분산보다 커짐에 따라 본래의 데이터 분포보다는 데이터 증강에 맞춰 최적화가 일어난다는 뜻으로 받아들이면 될 것 같습니다.
2. 데이터 증강의 공분산이 모든 차원에 대한 데이터 분산보다 작은 크기를 갖더라도, ‘implicit regularization’라고 하는 다양한 계층에서 가중치 행렬의 상호작용으로 인해 collapse가 발생된다. 이 부분은 바로 이해하기 힘드네요. 뒤에서 자세한 설명을 읽어봐야겠습니다.

저자들은 추가적으로 인코더를(representation space) trainable project를 사용하지 않고 최적화하는 DirectCLR이라는 contrastive learning 방법을 제안합니다. DirectCLR은 ImageNet에서 SimCLR(linear trainable projector 사용)를 능가하는 성능을 보였다고 합니다.

저자들의 contribution을 요약하자면 다음과 같습니다 :

• 저자들은 실험적으로 contrastive self-supervised learning 방법론들이 dimensional collapse 문제를 갖고 있는것을 밝혔습니다. dimensional collapse는 임베딩 벡터들이 모든 임베딩 공간을 충분히 활용하지 않고 특정 저차원 부분공간으로 압축되는 문제로, 가용한 표현력을 충분히 활용하지 않게 됩니다.
• 저자들은 contrastive learning에서 dimensional collapse를 유발하는 2가지 메커니즘을 밝혔습니다. 첫 번째로는 feature dimension에서의 강한 aumentation이고, 두 번째는 모델을 low-rank solution으로 유도하는 implicit regularization이라고 합니다.

Related Work

몇가지 중요한 부분만 짚고 넘어가겠습니다.

Self-supervised Learning

Self-Supervised Learning 학습법이 좋은 representation을 잘 학습해왔고 이제는 supervised learning 방법으로 transfer하는것 못지 않은 성능을 보여왔지만, 이런 방법들에 내제된 기본 역학은 아직 덜 탐구되어서 완전히 알려지지 않았다고 합니다. 이를 이해해보려는 여러 연구들이 있었는데, 결과적으로 contrastive learning 방법으로 사전학습된 representation은 일반적으로 downstream task에 유용하다는것이 밝혀졌으며, BYOL과 SimSiam과 같은 non-contrastive learning 방법들이 어떻게 collapse를 방지하는지 수학적으로 증명되었다고 합니다.

Implicit Regularization

[해당 논문] 에서는 deep linear network가 이론 및 실험적으로 low-rank solution을 유도할 수 있다는 내용을 다루었다고 합니다. 또한 일반적으로 over-parametrized neural netowrk는 좀 더 flat한 local minima를 찾게 되는 경향이 있다고 합니다[논문]. 해당 부분에서는 그냥 이런 이론이 있고 이 논문에서 다뤘어~ 하고 넘어가기에 정확히 어떤 내용인지 자세하게 이해하기는 어려웠지만, 신경망이 low-rank solution을 찾는 경향을 가질 수 있다고 이해하고 넘어갔습니다.

Dimensional Collapse

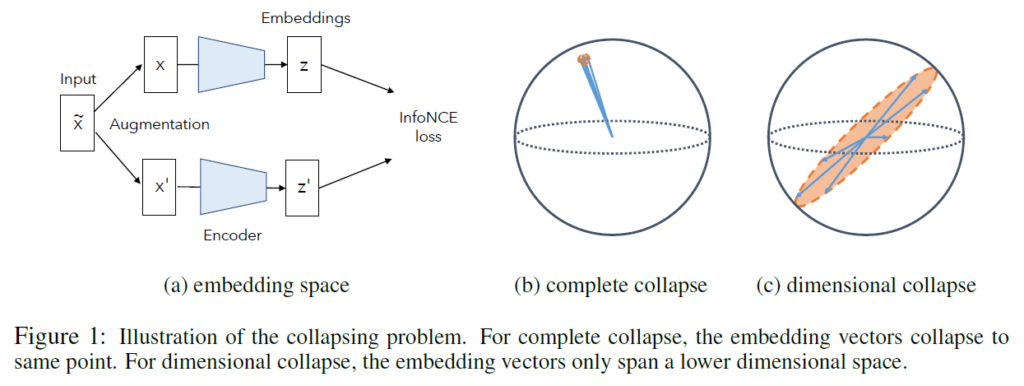
Self-Supervised Learning 방법 중 많은 방법들은 Figure 1(a)그림과 같이 증강된 이미지에서 얻은 임베딩 벡터 간 거리를 최소화함으로써 유용한 표현력을 학습하였습니다. 하지만 앞에서 밝였다시피, 이러한 방법을 사용하게 되면 생성한 representation이 수렴해 constant하게 되는 collapse가 발생하기 됩니다(Fig1(b)). Contrastive Learning은 negative pair를 도입해 다른 이미지에서 만들어낸 negative pair의 임베딩 벡터간 거리를 멀어지게 하여 complete collapse를 방지할수는 있었지만, Figure 1(c)와 같이 dimensional collapse 문제를 겪게 되는 것을 알 수 있었습니다. 이로 인해 활용할 수 있는 차원 수보다 적은 개수의 차원만을 사용하게 됩니다.

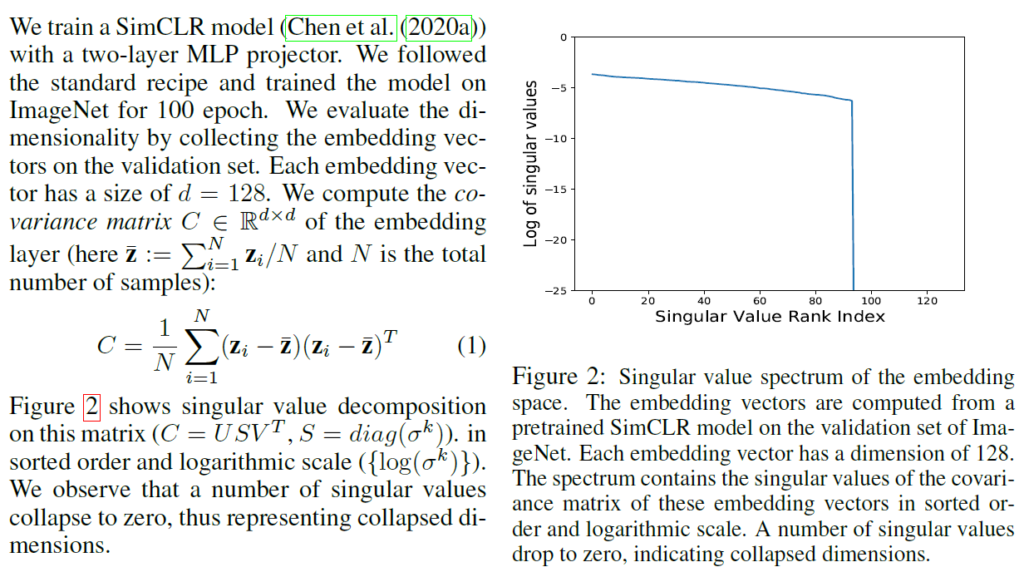
저자들은 SimCLR를 학습시킨 후 validation set의 임베딩 벡터(차원 d=128)를 이용하여 검증을 시도해보았는데, 위 수식 (1)번의 임베딩 계층에서의 covariance matrix C에서의 SVD(특이값 분해)를 해보았을 때 많은 singular values가 0으로 collapse되는것을 확인할 수 있었다고 합니다. 이것은 dimension이 collapse되었다는것을 의미한다고 합니다(Figure2를 참고하여 결국 임베딩 계층에서의 벡터들이 저차원으로만 span되도록 훈련된다는것을 보였다고 이해했습니다)

Dimensional Collapse Caused By Strong Augmentation

일단, 해당 섹션에서 contrastive learning의 데이터 증강이 입력 정보의 분포보다 커서 발생하는 임베딩 차원 collapse를 설명하기 위해 간단한 single linear netowork 상황을 가정합니다. 아래에서 x는 input vector를 나타내고, 네트워크는 가중치 행렬 W의 single linear layer이므로 임베딩 벡터 z는 z=Wx로 나타낼 수 있습니다. 그럼 contrastive learning에서 일반적으로 사용하는 InfoNCE loss는 다음과 같이 나타낼 수 있습니다.

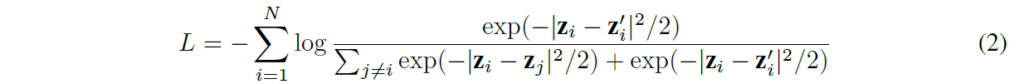
zi와 z’i는 두 branch에서 나온 임베딩 벡터 쌍이고, zj는 미니 배치 내부의 negative sample입니다. 많은 경우 zi와 z’i를 단위벡터로 normalize하는데, 이 경우 negative distance (-|zi – z’i|^2)/2를 zi와 z’i간 내적으로 대체할 수 있다고 합니다(벡터 간 cosine 유사도를 구하기 위해 normalize하고 내적을 취했다고 받아들이시면 될 것 같습니다)

이후에 장황한 수학적 증명이 나오는데.. 결론만 놓고 보면 해당 섹션에서는 수학적 정리를 통해 최종적으로 다음과 같은 결론을 도출해냅니다 : 강한 augmentation에 의해 임베딩 공간의 공분산 행렬은 low-rank가 된다. 결국 강한 데이터 증강으로 인데 dimensional collapse가 발생한다.

수학적 증명에 대한 내용은 다음과 같았습니다. 자세히 뜯어보고 싶으신 분들께서는 해당 논문의 appendix를 함께 참고하며 천천히 살펴보면 될 것 같습니다. 저도 처음부터 따라가며 이해해보려 노력해보았는데.. 부끄럽지만 중간부터는 이해가 안되어서 완전히 이해하는데는 실패했습니다. 너무 강한 데이터 증강이 contrastive learning에 있어 dimensional collapse를 유발할 수 있다는 결론만 확실히 기억해두려고 합니다. 증명의 흐름을 살펴보고 싶으신 분들은 다음 Lemma1과 Lemma2 부분을 훑어보시면 됩니다 :

Lemma 1은 single linear network이고 gradient descent가 매우 작은 간단한 상황에서 gradient dynamic을 통해 가중치 행렬을 기술한 것입니다.

이를 통해 간단한 신경망 상황에서 dimensional collapse가 발생하는 것을 보였습니다(저자들은 보다 복잡한 신경망 상황에 대해서 여전히 강한 augmentation이 collapse에 영향을 미치지만 위의 증명과는 다르게 해석된다는 말을 남겼습니다). 논문에는 여기서 추가적인 수치적 시뮬레이션 결과를 추가해 이론적 증명을 확인하려는 시도를 하였습니다.

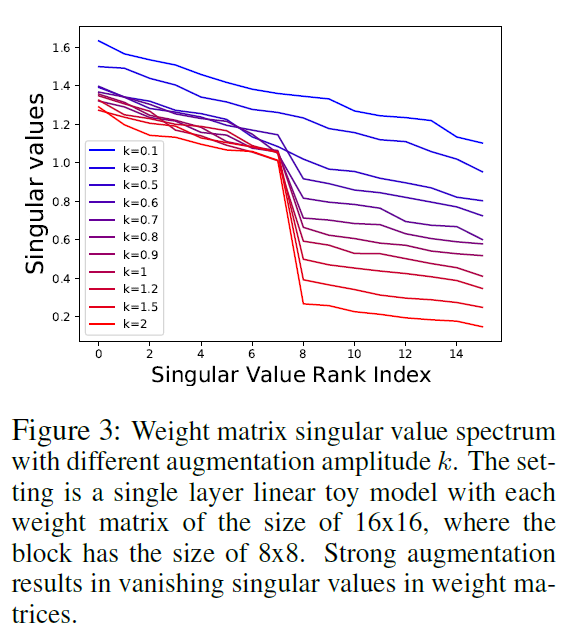
Figure 3은 다른 augmentation 강도에 따른 가중치 행렬의 singular value spectrum을 나타낸 것입니다. 이를 통해서도 linear network setting에서 강한 augmentation이 임베딩 공간에서의 dimensional collapse를 유발한다는 것을 확인할 수 있습니다.

Dimensional Collapse Cuased By Implicit Regularization

저자들은 증강이 강한 상황 이외에도 딥러닝 모델이 dimensional collapse를 겪는다는 것을 밖이고, 이 이유를 implicit regularization에서 찾습니다. 이는 over-parametrized linear network가 low-rank solution을 찾는 경향을 뜻한다고 합니다.

implicit regularization은 우리가 익히 아는 explicit regularization과 달리 별도의 penalty term이 없더라도 신경망에서 다른 인접 계층 행렬의 상호작용으로 인해 모델이 low-rank solution을 찾으려는 경향을 보인다는 것입니다. 논문에서는 W1,W2 간 상호작용을 확인하기 위해 특이값분해를 이용해 Alighment matrix(A)를 사용하여 증명을 시도합니다.

위와 같이 기술 할 수 있고 특이값 분해 후 인접 직교 행렬간의 상호작용을 전개하면 다음과 같다고 합니다.

저자들의 수식 전개를 따라가다 보면 결국 다음과 같은 결론을 도출하게 됩니다 : 가정한 상황에서 W2W1가 low-rank로 수렴하고, 임베딩 벡터의 공분산 행렬의 singular value spectrum C 또한 low-rank로 가게 되어, 이것으로 정의되는 embedding space 또한 저차원이 되어 dimensional collapse가 일어난다.

간단한 2계층 선형 신경망의 훈련 이후 Aligned matrix를 시각화하면 identity matrix로 수렴함을 확인할 수 있다고 합니다.

DirectCLR

일반적으로, contrastive learning에서 encoder 뒤에 projector를 도입하는 것은 representation 학습 및 downstream task 적용에 좋은 영향을 끼친다고 알려져 있습니다. 실제로 SimCLR를 projector 없이 학습하면 다음과 같은 결과를 얻을 수 있었습니다(projector가 없으면 SimCLR의 dimensional collapse가 심화되었습니다)

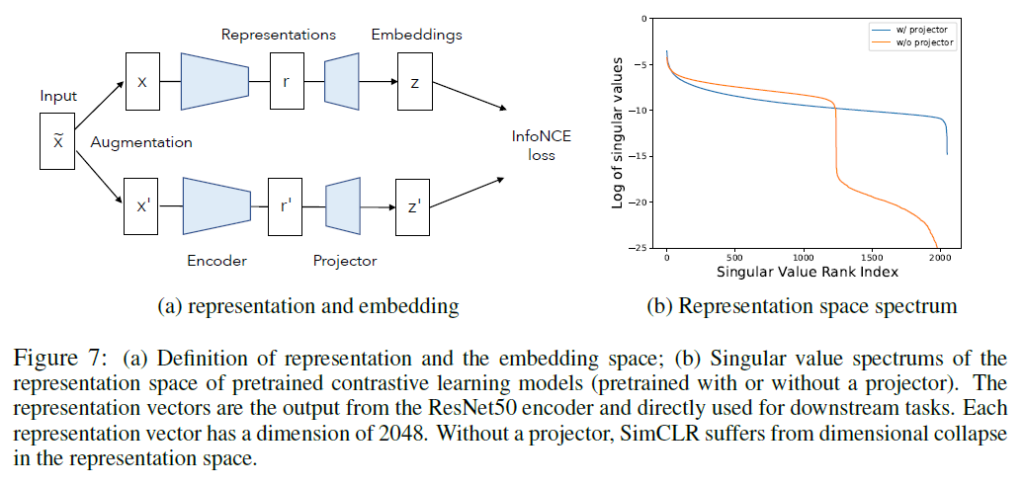
이에 DirectCLR에서는 projector의 어떤 성분이 dimensional collapse를 방지하는데 영향을 주는지 확인하기 위해 projector를 없애고 representation space를 직접적으로 최적화해 성능을 확인합니다. representation 벡터의 일부를 InfoNCE loss에 직접 전달해 학습을 진행하는 것입니다.

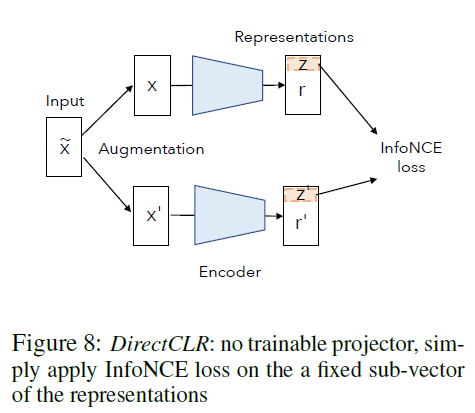
그림에서 확인할 수 있듯 DirectCLR은 representation z=r[0 : d0]에서(d0은 하이퍼파라미터) subvector를 고정하고 학습을 진행합니다. 이를 통해 학습을 하게 되면 projector가 없음에도 1-layer linear projector보다 높은 Accuracy를 달성할 수 있었습니다.

Figure 9를 참고하면, 학습한 representation space의 스펙트럼을 확인하였을 때 DirectCLR 방법이 SimCLR에서 trainable project를 사용한것과 유사하게 dimensional collapse를 어느 정도 완화하는것을 확인할 수 있습니다.

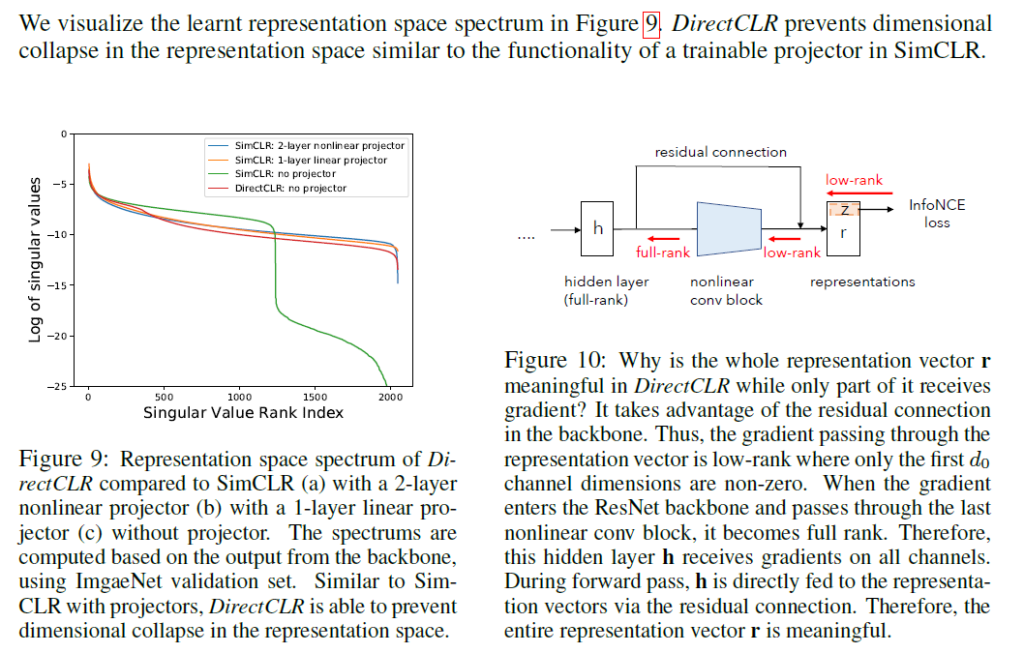
Figure10에서는 graidient 흐름에 있어서는는 몇몇 low-rank 벡터들이 중요하지만 그 이외의 representation 요소들 모두 표현력에 있어 중요하다는 것을 설명하는 부분입니다.

Conclusion

해당 논문에서 저자들은 contrastive learning 역시 dimensional collapse 문제를 겪는다는 것을 지적하고, 수학적 증명을 통해 1. 너무 강한 데이터 증강 및 2. 신경망 내부 계층간 행렬 연산 상호 작용(implicit regularization)이 contrastive learning 상황에서의 dimensional collapse를 유발한다는 것을 보였습니다. 그리고 이를 개선한 DirectCLR을 제안했습니다.

SimCLR 논문은 강력한 이미지 증강이 좋은 성능 개선에 좋은 영향을 미친다고 강조했었는데, 원형과 너무 동떨어지게 되는 augmentation을 적용하게 될 때는 다시 한 번 숙고하는게 좋을 것 같습니다.

논문을 읽어 이해한 대로 최대한 리뷰에 담아보고자 했는데 논문을 깊이 이해하지 못해 리뷰에 논리적 흐름을 충분히 담지 못했다는 느낌이 듭니다. 수학 공부 열심히 해야겠네요… 그래도 contrastive learning에서 발생하는 dimensional collapse에 대한 성질을 더 자세히 알 수 있었고, 해당 성질들을 잘 기억해두고자 합니다 나중에 여유가 된다면 다시 한번 수식을 천천히 뜯어보며 이해하려고 노력해야 할 것 같습니다.

감사합니다.