[ICLR 2023 Oral] Towards Stable Test-Time Adaptation in Dynamic Wild World

오늘 리뷰할 논문도 마찬가지로 TTA와 관련된 논문입니다.
제목 속의 Dynamic Wild World 라는 워딩이 매력적으로 보여서 읽어보게 되었는데, contribution적인 부분 보다도 wild world상황에서 등장할 수 있는 여러 시나리오에 대한 실험적 분석 내용이 많은 부분을 차지하는 그런 논문이였습니다.
그럼 리뷰 시작하도록 하겠습니다.

---

1. Introduction

Domain Adaptation task의 목표는 명확합니다. 학습때 보는 source dataset과 평가때 마주하는 target dataset 사이의 domain distribution shift를 해결하는 것이죠.
이러한 DA를 어느 시점에 어떤 세팅으로 수행하느냐에 따라 UDA, DG, TTA 등 여러 갈래로 나뉘어집니다.

이들 중 모델의 실시간성을 고려하면서 test 단계에서 online 방식으로 모델을 update 해 나가는 연구는 크게 2가지가 존재합니다. Test-Time Training (TTT), 그리고 Fully Test-Time Adaptation(TTA) 입니다. 이 둘에 대해 간단하게 살펴보겠습니다.

i) Test-Time Training (TTT)

모델을 우선 source dataset으로 pretrained 시킵니다. 이를 f_{\theta}(x) 라 합니다. f_{\theta}(x)를 test sample에 대해 adaptation 시키기 위해 TTT는 크게 training 단계와 test 단계로 나눠서 진행합니다. training 단계에서는 source dataset을 사용해서 모델을 추가 학습시키게 되고, 이때 학습에 적용되는 loss는 Cross Entropy Loss와 self-supervised loss 가 적용됩니다. self-supervised loss로 어떤 loss가 사용되는지는 논문들마다 조금씩 상이한데, 예를 들어 rotation 을 예측하는 rotation loss가 존재합니다. 식은 아래와 같습니다.

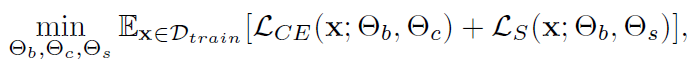
학습되는 파라미터는 크게 \theta_b, \theta_c, \theta_s로 구성되어 있습니다. \theta_b는 task-shared parameter로 CrossEntropy와 self-supervised loss 둘 모두에 대해 학습되는 parameter입니다. 반면 \theta_c/latex], [latex]\theta_s는 각 loss별로 개별적 학습되는 parameter 입니다.

위 loss를 통해 잘 학습된 모델을 사용하여 test 단계가 진행되게 됩니다. test 단계에서는 입력으로 들어오는 test sample에 대해 앞선 training 단계에서 설계한 self-supervised task로 추가적인 update가 진행되게 됩니다.

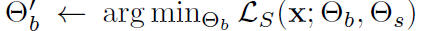
설계한 self-supervised task 및 self-supervised loss를 사용해서 \theta_b 를 \theta'_b로 update 하게 됩니다. 이후 최종적인 예측은 방금 update된 \theta'_b와, training 단계에서 미리 학습된 \theta_c를 사용해서 수행하게 됩니다.

ii) Fully Test-Time Adaptation (TTA)

앞서 설명한 TTT에는 3개의 치명적인 단점이 존재합니다.
i) 추가적인 self-supervised task (auxiliary task) 의 설계 및 수행이 수반된다.
ii) Adaptation 수행 시 source dataset으로 직접 접근해야 한다.
iii) Fully TTA 대비 더 많은 backward 연산이 수행된다.

이러한 기존 TTT의 단점을 극복하기 위해, TENT 방법론은 2021년에 Fully TTA를 최초로 설계하였고 이는 TTA 분야의 baseline격 논문으로 자리매김 하였습니다. (리뷰 참고)

TTT와 달리 TTA는 adaptation 수행 시 source dataset으로의 접근이 필요 없고, aulixiary task도 수행하지 않기 때문에 훨씬 더 효율적이죠.
오늘 리뷰드릴 논문도 Fully TTA 분야 논문입니다.

---

Fully TTA 분야는 TENT 방법론을 발판 삼아 빠른 발전을 이루어 나갔습니다. 하지만 본 논문의 저자들은 앞선 연구들이 실제 상황, 즉 dynamic wild world 를 고려하지 않고, 실제랑은 조금 동떨어진 mild test setting 상황에서 학습 및 평가를 진행했다고 합니다. 아래 Figure에서 이와 관련된 설명을 모두 수행하니, 그림을 통해 살펴보도록 하겠습니다.

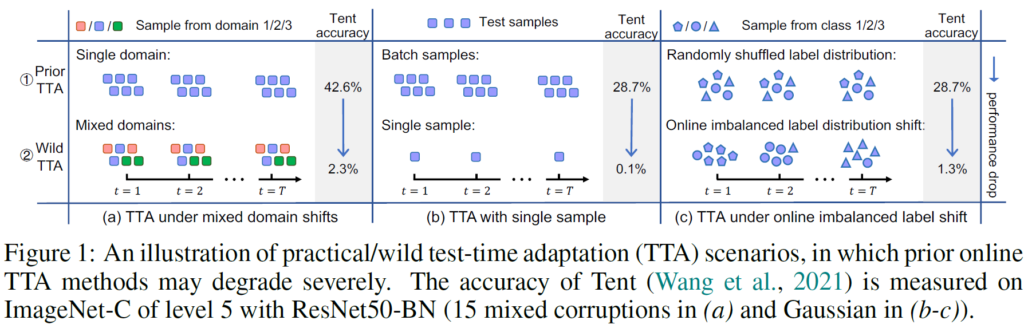
기존 방법론 중 TENT를 선정하여 실험을 진행합니다. ImageNet->ImageNet-C 로의 TTA 성능을 평가하였고, ResNet50-BN 모델을 사용합니다.
저자들은 앞선 TENT 연구가 실제 wild world 상황을 고려하지 못했다는 것을 크게 3가지 측면(a~c)으로 나누어서 설명합니다.

Fig1-(a)
실제 world에서는 한 batch 내에 여러 domain들이 혼합될 수 있습니다. 하지만 TENT 에서는 단일 domain 상황만을 다뤘습니다. 그렇기 때문에 wild TTA 상황 속 mixed domain을 마주했을 때 성능이 2.3% 밖에 나오지 않는 결과를 보여주죠.
TENT를 포함한 많은 TTA 방법론들은 batch norm update 방식을 사용합니다. 이때 BN layer에서 중요한 요소 중 하나가 batch 내 통계값(평균, 분산) 을 통해 data distribution을 normalization을 수행하게 되는데, 여러 domain이 혼합된 상황에서도 동일한 통계값으로 normalization이 수행되기 때문에 성능의 하락이 발생한 것입니다.

Fig1-(b)
TTA의 실시간성을 보장하기 위해 입력으로 들어오는 test batch size가 작거나, 혹은 1일 수도 있습니다. 이 경우에 BN layer update 방식으로 동작하는 앞선 방법론들의 경우 성능의 하락이 발생할 수 있고, 실제 실험 결과에서도 0.1%라는 낮은 성능을 기록하였습니다. BN layer는 큰 batch size를 가질수록 더 robust하게 동작하는데, 낮은 batch size의 경우 이를 만족하지 못합니다.

Fig1-(c)
실제 world에서는 한 batch 내에 동일한 class 분포를 가지는 것이 아닌, class-imbalance한 상황이 당연히 등장하기 마련이고, 이에 대한 고려가 필요합니다. 하지만 TENT는 그러지 못했고, 성능도 1.3%를 보이고 있습니다.

---

본 논문에서는 여러 실험을 통해 앞선 방법론들에서 많이 사용하던 BN layer 가 실제 wild scenario 속 TTA를 수행하는 상황에서 obstacle로 동작한다는 점을 밝혀냈습니다. 그리고 Batch norm가 아닌, batch-agnostic norm layer인 Group Norm(GN), Layer Norm(LN) 이 안정적인 TTA를 수행하는 것에 있어서 훨씬 더 효과적이라는 것을 실험을 통해 증명합니다.

하지만 GN/LN layer가 항상 성공적인 TTA를 수행하는 것은 아니라고 합니다. 급격한 domain shift가 발생하게 되면 모든 test sample 을 동일한 class로 예측해 버리는, model collapse 현상을 관찰했다고 합니다.
그리하여 이를 해결하기 위한 Sharpness-Aware and Reliable (SAR) entropy minimization 기법을 설계하게 됩니다. 몇몇 noisy test sample이 큰 gradient를 발생시키고, 이 때문에 model collapse 현상이 발생하게 됩니다. 이를 위해 large & noisy gradient를 가지는 test sample을 filtering 하게 됩니다.
그리고 필터링 되고 남은 test sample에 대해 모델을 단순 optimize 하는 것이 아닌, flat minimum 지점으로 optimize 함으로써 조금 더 안정적인 adaptation을 수행하고자 하였습니다.

---

2.1. What Causes Unstable Test-Time Adaptation

Batch Normalization Hinders Stable TTA

앞선 많은 TTA 연구들은 test 단계에 입력으로 들어오는 test sample 에 대해 모델을 성공적으로 adapation 하기 위해 BN layers 를 update 하였습니다. BN layer에 관여하는 연산은 크게 Normalization -> Transformation 으로 진행됩니다. Normalization 에서는 BN layer 기준 입력 data들의 통계값(평균, 분산) 을 구해서 분포를 평균0 분산1로 만들어주게 되며, Transformation 에서는 learnable affine parameters인 \gamma, \beta를 사용하여 새로운 분포로 변형해주게 됩니다.

wild world TTA 상황 속에서, 이러한 Batch Normalization 기반 방법론을 사용하게 되면 크게 3가지 문제점이 있습니다. 이는 위 Fig.1 에서도 설명드린 내용이므로 간략히 핵심만 요약하겠습니다. 각각 Fig.1 의 (a),(b),(c)에 매치됩니다.
i) 이상적으로라면 각 batch 내 sample들이 유사한 분포를 가지는 상황 속에서, large batch norm이 동작하게 됩니다. 하지만 한 batch내 서로 상이한 분포를 가지는 test sample들이 섞여있는 경우 성능이 하락하게 됩니다.
ii) 계산되는 통계값(평균, 분산)은 batch의 크기와 직결됩니다. 더 큰 batch size일 수록 더 다양한 distribution을 커버하게 되죠. 반대로, small batch size일 경우 성능이 하락하게 됩니다.
iii) 한 batch 내 test sample이 class-imbalance한 상황일 경우 해당 class 로 bias된 통계값을 얻게 되고, 이 경우에도 성능이 하락하게 됩니다.

저자는 BN layer의 위 3가지 문제점을 꼬집으며,
batch-agnostic한 norm layer인 Group Norm(GN) & Layer Norm(LN) 이 TTA 수행에 더 적합하다고 주장합니다.

---

Online Entropy Minimization Tends to Result in Collapsed Trivial Solution (Predict All Samples to the Same Class)

비록 BN layer에 비해 GN, LN layer가 더 안정적인 TTA를 수행하긴 하지만, 급격한 domain shift가 발생하는 상황에서는 여전히 실패 case가 발생한다는 것을 실험적으로 보입니다.

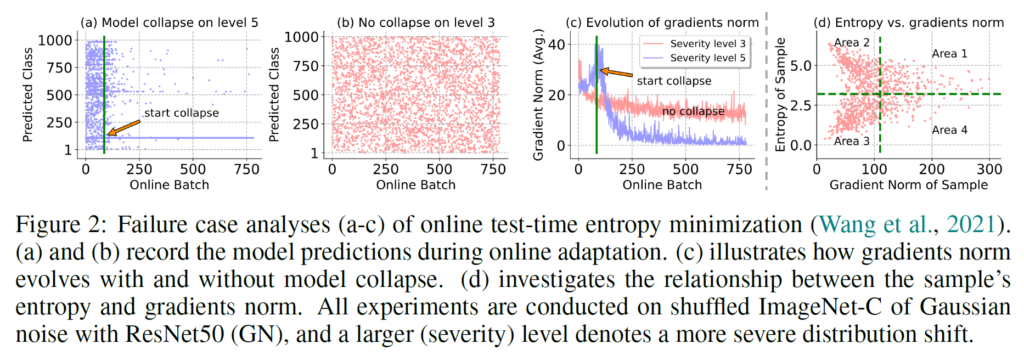
위 실험은 ResNet50 with GN(Group Norm) 모델을 통해 ImageNet-C에서의 TTA 성능을 나타낸 것입니다. ImageNet-C는 기존 ImageNet에 corruption(왜곡)을 부여한 dataset입니다. 위 실험에서는 Gaussian corruption을 적용하였고, 그 강도에 따라 level 1~5로 나누어 진다고 보시면 됩니다.

(a) level 5, 즉 강한 corruption을 부여했을때의 결과입니다. 급격한 domain shift가 발생한 상황을 표현했다고 볼 수 있죠.
x 축이 나타내는 것은 Online Batch 수행 횟수, 즉 time 축이라고 생각하시면 됩니다. x축 기준으로 0부터 출발해서 초록색 line 지점까지는 1000개의 class에 대해 다양한 prediction을 수행하는 것을 볼 수 있습니다. 하지만 초록색 line 이후 시점부터 model collapse가 시작되고, 예측 결과가 하나의 class로만 bias되는 현상이 발생하게 됩니다.

반면 (b)에서는 level 3의 corruption만을 부여했기 때문에 (a)와 같은 model collapse 현상은 발생하지 않았네요.

저자는 이런 현상을 분석하기 위해 adaptation 단계 속 gradient의 l2 norm 값을 그래프로 그려 보았습니다. 위 figure 속 (c) 처럼 말이죠. (c)에서 핑크색 그래프, 즉 정상적인 adaptation이 진행된 level 3의 그래프는 정상적으로 잘 수렴하고 있습니다.
반면 파랑색 그래프, 즉 level 5의 corruption 속에서 model collapse가 발생했을때의 그래프를 보시면 gradient l2-norm의 값이 collapse 되기 직전에 급격하게 튀어 올랐다가, 이후 급격하게 감소하는 현상을 살펴볼 수 있습니다. 저자는 해당 실험 결과를 통해 특정 test sample이 large gradient를 발생시켰고, 이 때문에 model collapse 현상이 발생하게 되었다고 합니다.
그리고 해당 문장 속 특정 test sample이 의미하는 바는 level 5 corruption, 즉 급격한 domain shift가 발생한 test sample이 되겠죠.

---

2.2. Sharpness-Aware and Reliable Test-Time Entropy Minimization

위 2.1 절의 실험 결과가 의미하는 바는, large gradient를 발생시키는 특정 test sample 때문에 GN/LN을 사용했음에도 불구하고 model collapse 현상이 발생한다는 것이였습니다. 이를 해결하기 위해 직관적으로 large gradient를 발생시키는 test sample을 필터링하거나, gradient clipping을 수행하는 방식을 생각해낼 수 있습니다.

하지만 어떤 모델, hyperparam을 사용하는 지에 따라 gradient의 scale이 매우 상이하기 때문에 전체를 아우르는 일반적인 해결책을 설계하기는 어렵습니다.

Reliable Entropy Minimization

이를 해결하기 위해 저자들은 entropy 개념을 가지고 와서, entropy loss와 gradient norm 사이의 관계를 분석하였고, entropy 측정 값에 기반해서 large gradient 샘플을 필터링하고자 하였습니다.
entropy는 모델 예측의 불확실성으로, 총 class 갯수가 C라고 한다면 (0, ln C)와 같이 범위가 매우 명확합니다. scale이 불분명한 gradient norm 값과는 달리 말이죠.

그렇기 때문에 저자들은 특정 threshold를 기준으로 entropy 값을 필터링 하였고, 이를 통해 large gradient 값을 가지는 test sample을 필터링 하고자 하였습니다.

entropy와 gradient norm 사이의 관련성을 나타낸 그래프가 위 Fig2.(d) 입니다. 편의를 위해 아래에 다시 첨부하겠습니다.

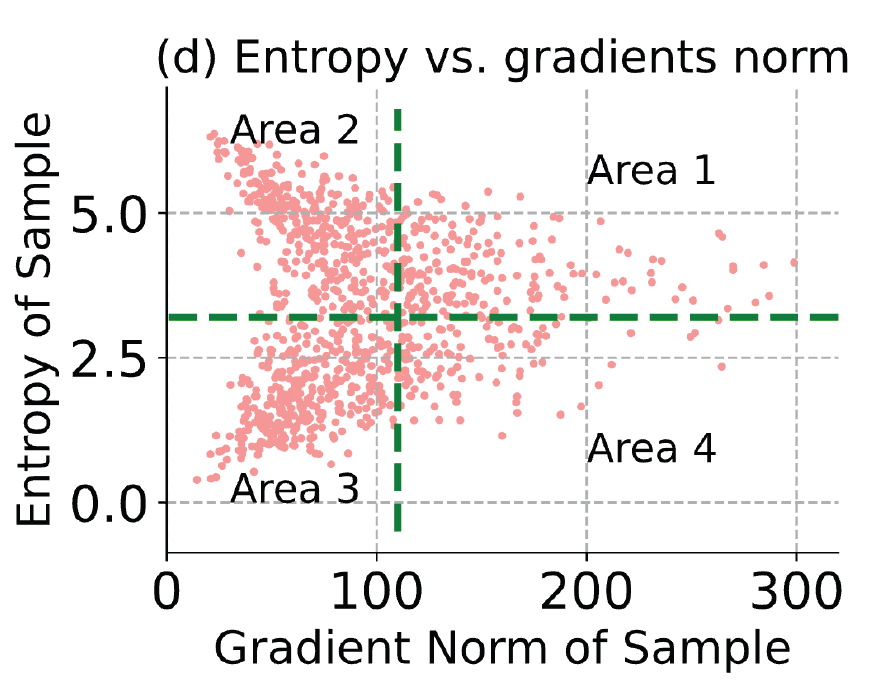
우선 특정 threshold 보다 높은 entropy 를 가지는 sample들은 모두 filtering 대상으로 선정하였다고 합니다.
""높은 entorpy = 낮은 confidence == unreliable sample"" 이라고 정의했기 때문입니다.
수식으로 표현하면 아래와 같고, 위 그래프를 기준으로 Area 1, 2 영역 속 test sample들은 모두 filtering되겠네요. E()는 Entropy Loss 입니다.

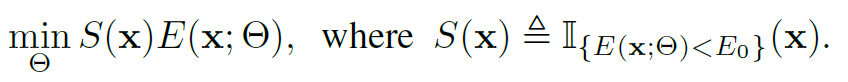
\mathbb{1}는 Indicator function을 의미합니다. 그리고 S(x)는 Entropy가 threshold E_0보다 낮은, reliable한 test sample을 의미하죠. 결과적으로 Area 1,2에 포함된 unreliable한 test sample은 제외하고, reliable한 test sample만을 사용해서 Entropy Minimization 기반 TTA를 수행합니다.
이때 threshold E_0는 0.4*ln(1000) 을 사용했다고 합니다. class 갯수 C에 따라 entropy의 범위가 바뀌기 때문에 threshold hyperparameter도 C가 반영된 값일 줄 알았는데, 고정 상수였네요. 계산해보면 약 2.76,,, 입니다.

Sharpness-aware Entropy Minimization

위 과정을 통해 Area 1,2 영역의 test sample은 모두 filtering 되었고, Area 3,4 영역의 test sample을 사용해서 TTA를 수행할 수 있습니다.

하지만 이상적으로라면 Area 3 영역의 test sample만을 사용해서 model update를 수행해야 합니다. Area 4 는 large gradient norm 을 가지는 test sample이고, 안정적인 adaptation에 방해가 되기 때문이죠. 이 상황 속 Area 3과 4를 구분지을수 있는 기준이 있다면 좋겠지만, 앞서 언급드린 모델별 상이한 gradient norm 의 scale 때문에 불가능합니다.

이에 대한 대안책으로, Area 4의 test sample을 filtering하지 않고 그대로 사용하되, 그들이 발생시키는 large gradient에 대해 모델이 민감하지 않고(insensitive) robust하게 update를 수행하도록 설계합니다. 모델을 단순 update 하는 것이 아닌, 추가적인 제약을 걸어서 loss graph내의 flat한 영역으로 optimize를 하도록 합니다. sharp한 영역이 아닌 flat한 영역에서는 unreliable test sample이 large gradient를 발생시킨다 할지라도 훨씬 더 robust하고 일반화된 성능을 보장하기 때문이죠.

저자들은 이를 위해 '[ICLR 2021] Sharpness-Aware Minimization for Efficiently Improving Generalization' 논문에서 제안한 SAM 이라고 하는 기법을 가져와서 사용합니다. 해당 기법은 모델이 sharp한 minimum으로 빠지지 않도록 적절한 optimization을 수행합니다. shap한 minimum이라 함은, 조금의 update만 수행이 되어도 loss가 팍 튈 수 있는, 그런 날카로운 꼭짓점 영역을 의미한다고 보시면 됩니다. 반대로 본 논문에서 optimize하고자 하는, flat한 영역은 어느정도 큰 update가 수행된다 한들 loss가 팍 튀지않고 robust하게 update 되는 그런 영역을 의미하겠죠.

사실 제가 ICLR 2021 paper를 읽은 것도 아니고, 제 수학 실력 이슈로 인해 수식적 설명이 미흡할 수 있습니다. 수식적 설명은 부족하더라도 figure를 통해 flat mimimum에 대한 설명을 최대한 해 보겠습니다.

우선 아래 수식을 통해 \theta를 기준으로 \epsilon 만큼의 범위에 대해 Entropy를 maximization 해 주는 \epsilon을 찾습니다. 이때 \epsilon의 l2-norm이 \rho 보다 작은 \epsilon에 대해서만 maximization을 수행하게 되며, \rho는 0.05를 사용했다고 합니다.

본 논문에서 표현하길 우리가 피해야 하는 sharpness는 entropy의 최대 변화로 정량화할 수 있고, 반대로 flat minimum으로 optimize하기 위해선 Entropy를 maximization 해 주는 \epsilon을 찾은 뒤, 찾은 \epsilon를 적용해서 반대로 entropy를 minimization 해 주면 된다고 합니다.

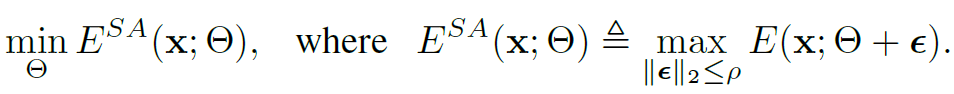
그리고 위 수식에서 Entropy Maximization을 해 주는 \epsilon를 찾기 위해 taylor expansion 을 적용한 수식이 아래와 같고,

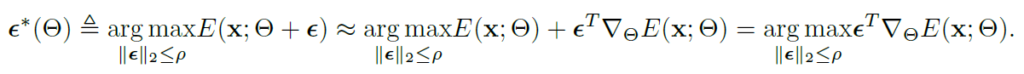
결국 근사화를 통해 해를 구하면 아래와 같다고 합니다.

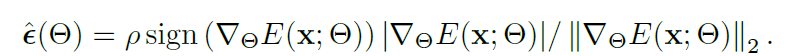
구한 \epsilon 을 위 식 3에 대입하게 되면 최종 entropy 수식은 아래와 같습니다.

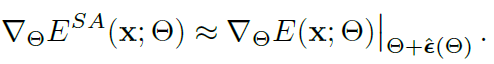
그리고 이를 minimization 해주는 것이 최종 loss function 입니다.

---

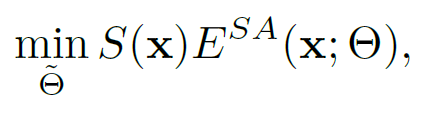
위 복잡한 수식을 아래 figure를 통해 간략하게나마 설명해보자면,,

현재 지점인 W_t를 기준으로, 단순 update를 진행하면 sharp minimum인 W_{t+1}로 update 되게 됩니다. 이를 방지하고자 Entropy를 maximization 해 주는 \epsilon을 찾은 뒤, 이를 통해 W_{adv} 지점으로 이동하고, 해당 지점에서 gradient 방향을 계산하게 됩니다.
그리고 계산된 gradient 방향을 다시 현재 지점인 W_t 로 가져와서 optimization을 수행하는 방식으로 동작합니다. 최종적으로는 W_{t+1} 지점이 아닌, W^{SAM}_{t+1} 지점으로 update 되게 됩니다.

---

그리고 부가적으로 Model Recovery Scheme 기법도 간략하게 설계합니다.
아래 Algorithm 1 의 line과 함께 설명하겠습니다.

동작 방식은 간단합니다. 매 batch 에 대해 entropy e_m를 계산하고 이를 moving average 방식으로 update 해 나갑니다. (line 11)
그리고 이때 e_m 이 threshold e_0 (0.2 사용) 보다 낮은 경우에 대해, model이 이미 collapse 되어서 매우 낮은 entropy loss가 계산된다고 가정합니다. 그리고 이렇게 model collapse가 되었다면 model의 weight를 초기 상태로 되돌려버립니다. (line 12-13)
(TTA 논문을 읽으면서 model을 아싸리 초기 상태로 되돌려버리는 방식이 심심찮게 등장하네요)

---

3. Empirical Studies of Normalizatoin Layer Effects in TTA

본 논문은 intro에서부터 기존 BN layer방식의 문제점에 대해 3가지 예시를 들면서 GN/LN layer의 효과를 주장하고 있습니다. 본 섹션에서는 wild test setting 속 각 Norm Layer들 끼리의 비교를 다양한 관점에서 수행합니다.

1) Norm Layer Effects in TTA Under Small Test Batch Sizes

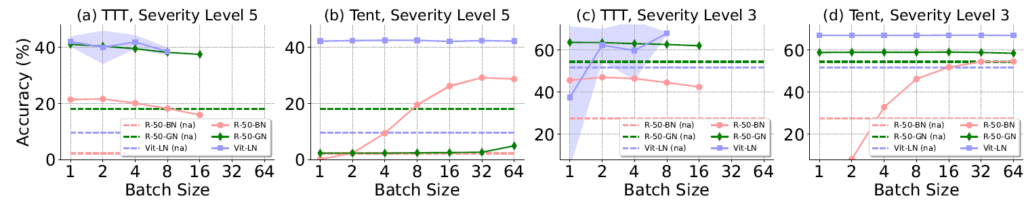
본 실험은 small batch size에서 각 norm layer에 대한 결과를 보여줍니다.
(a), (c)는 Test-Time Training (TTT)에 대한 실험 결과를,
(b), (d) 는 Fully Test-Time Adaptation 방법론 중 하나인 Tent에 대한 결과입니다.
또한 위 그래프에서 점선은 아무런 adaptation을 적용하지 않은 것이고, 실선은 adaptation 기법을 적용한 것입니다. 그리고 선의 색상은 norm layer의 차이를 의미하구요.

(b),(d) - Tent 결과를 보시면 batch size에 따른 성능 변화를 알 수 있습니다. 주황색 실선인 ResNet50-BN의 경우 낮은 batch size에 대해서 큰 폭의 성능 하락이 관찰되네요.
(물론 (b)에서 ResNet50-GN의 성능은 완전 0이긴 합니다만,, (d)에서는 높은 성능을 보여줍니다)

(a),(c) - TTT 결과를 살펴보겠습니다.
세가지 방법론 모두 failure case 없이 어느정도 준수한 성능을 보여주고 있습니다.
하지만 파랑색 실선, Vit-LN을 보시면 그래프 뒤쪽으로 배경 영역이 넓게 칠해진 것을 볼 수 있습니다. 위 그래프 생성 시 3가지 random seed에 대한 결과를 모두 반영하였는데, Vit-LN는 random성에 따라 매우 민감해서 편차가 큰 결과를 보이는 것을 알 수 있습니다.

2) Norm Layer Effects in TTA Under Mixed Distribution Shifts

위 실험에서는 하나의 test batch 내에 여러 domain이 mixed 된 채로 구성이 될 때, 각 norm layer 별 성능을 분석한 결과입니다.
Intro에서 언급드렸다시피, 기존 BN layer 기반 방법론은 하나의 test batch가 모두 동일한 domain data로 구성되었다는 가정이 있었습니다. 하지만 실제 wild-world 에서는 하나의 test batch 내에서도 여러 domain 이 섞여서 입력으로 들어올수도 있기 때문에, 이를 살펴보기 위한 분석 실험입니다.
위 그래프를 해석할 때, 동일 방법론 기준 Avg.adapt (한 batch 내 동일 domain) 성능과 Mix adapt (한 batch 내 mixed domain) 의 성능 차이가 클 수록 mixed distribution shift에 robust 하지 못하고 민감한 모델이라고 생각하시면 됩니다.

강 방법론 별 빨간색 그래프와 파란색 그래프의 차이를 기준으로 보시면, 확실히 BN layer를 사용한 모델에서 더 큰 성능 gap이 있는 것을 볼 수 있습니다. 아무래도 단일 batch 내의 통계값(평균, 분산)을 계산해서 normalization을 수행하기 때문에 여러 distribution 을 가지는 sample들이 하나의 batch 내에 동시에 있는 경우 큰 성능 하락이 발생하게 됩니다.

3) Norm Layer Effects in TTA Under Online Imbalanced Label Shifts

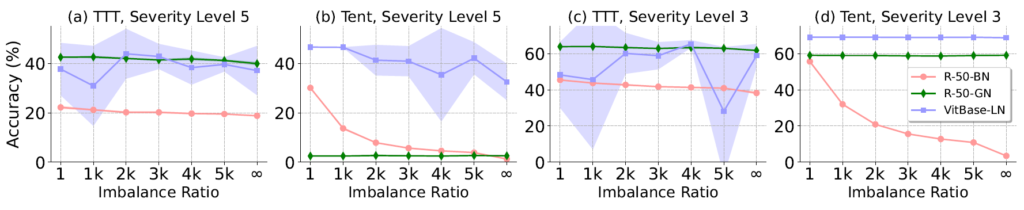
class-imbalance 와 관련된 분석 그래프입니다.
x축은 class imbalance 비율을 나타낸 것으로, 우측으로 갈 수록 더욱 imbalance한 상황인 것입니다.

위 결과에서 GN/LN 이 모든 경우에 대해 BN보다 더 좋은 결과를 보였다고 볼 수는 없습니다. 가령 (b) 에서 초록색 GN 결과를 보시면 성능이 0에 수렴하죠.

하지만 class-imbalance에 따른 결과를 관찰해야 하는 관점 속, 평균적으로 imbalance 비율이 커질수록 성능 degradation 폭이 큰 쪽은 명백히 핑크색-BN 입니다.

이는 위 (2)에서도 설명드렸다시피 batch 내 data를 사용하여 통계값을 계산하는 BN layer의 특성 때문이지요.

---

4. Experiment

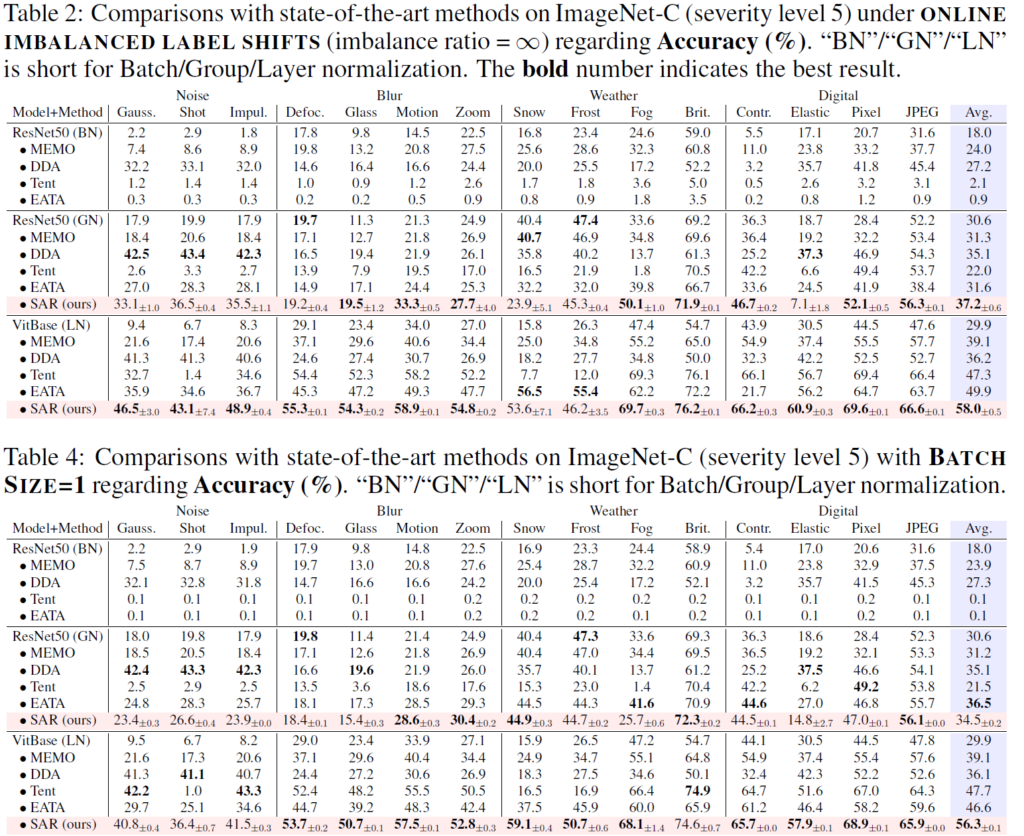
Table 2는 class imbalance 상황에서의 결과를,
아래 Table 4는 small batch size(1) 에서의 결과를 보여줍니다.

위 Table에서는 BN layer 대신 GN/LN으로 대체하였을때 모든 방법론에서 성능 향상폭이 큰 것을 볼 수 있습니다.
아래 Table도 유사한 결과를 보여주고요.
특히 위, 아래 Table 모두 BN 에서는 매우 낮은 성능, 0에 가까운 성능을 보여주는 것으로 보아 실제 wild-setting 에서 BN 이 아닌 타 Norm Layer의 사용이 더 적절할 수 있겠네요.

---

네 오늘은 제목에 이끌려 읽게된 Wild world 상황을 고려한 TTA 기법에 대한 분석적 논문을 리뷰해 보았습니다.
사실 가벼운 마음으로 시작했는데,, 수식적으로 복잡한 부분도 몇 존재했고 실험도 되게 많아서 읽는데 꽤 많은 시간을 투자한 것 같습니다.

하지만 TTA를 입문한 지 아직 얼마 되지 않은 제 입장에서 다양한 관점에서의 많은 실험들을 수행한 본 논문이 꽤나 값졌습니다. 나중에 두고두고 돌아볼 거 같네요.
(사실 제가 담지못한 실험이 많이 있는데,, 나중에 세미나 준비를 하면서 기회가 된다면 추가하도록 하겠습니다)

본 논문에서 하고자 하는 말은 결국, wild world 상황 속 여러 조건 (3가지) 을 충족하기 위해선 BN layer는 부족하다. 타 norm layer(GN, LN) 를 사용해야된다, 다만 이들도 만능은 아니기에 추가적인 처리(gradient 관련 처리) 를 해야한다.
뭐 이정도이지 않을까요.

Contribution 적으로는 뭐 엄청나게 novel 하지는 않지만, 실험 내용이 풍부한 논문이였습니다. 마무리하기 전에 드는 생각이,,,,, 그렇다면 왜 아직도 GN./LN이 아닌 BN 기반으로 연구가 진행되고 있는걸까요? 이게 2023년 논문이라 아직 반영이 안된걸까요?

아무튼 리뷰 마치도록 하겠습니다. 감사합니다.