[ICCV 2023] Boosting Multi-modal Model Performance with Adaptive Gradient Modulation

Introduction

저자들은 최근 몇 년간 멀티모달 연구가 활발하게 진행되었고, 상당한 발전을 이루었음에도 여전히 challenge하다고 언급하였습니다. 단일 모달의 한계를 뛰어넘기 위해 모달리티 간의 fusion을 진행하였음에도 그렇게 완성된 멀티모달 모델은 단일 모달에 비해 그렇게 뛰어나지는 않으며, 각 모달리티의 potential을 충분히 학습하지 못하다는 것입니다. 예를 들어 Delbrouck et al., 2020는 CMU-MOSEI 데이터셋에서 멀티모달 모델과 단일 모달 모델간의 성능 비교를 진행하였는데요, 멀티모달(text+audio+video)의 정확도가 단일 text 모달 성능보다 약 1%정도의 성능 향상만을 이루었으며, 다른 여러 멀티모달 데이터셋에서도 이러한 경향성이 관찰되었다고 합니다.

멀티모달 모델에서 각 모달리티의 정보를 효율적으로 활용하지 못 하는 원인은 여러 모달리티 중 상대적으로 영향력이 큰 모달리티가 존재하여 학습 시 다른 모달리티의 활용을 억제하기 때문으로, 이를 modal competition이라 합니다. 구체적으로는 여러 모달리티를 동시에 학습할 때 수렴 속도의 차이가 발생하며, 학습을 통해 특정 모달리티가 먼저 수렴하는 경우, 모델 전체의 gradient를 크게 감소시켜 아직 학습이 완료되지 않은 다른 모달리티의 학습이 어렵도록 하는 것이라고 하며 Huang et al., 2022은 이를 수학적으로 증명하였다고 합니다.

이러한 modal competition 문제를 해결하기 위해 본 논문의 저자들은 adaptive gradient modulation(AGM)이라는 방법을 제안하였습니다. AGM은 shapley value를 기반으로 멀티모달 모델에 각 모달리티의 영향력을 균형 있게 조절하여, 이를 통해 모든 모달리티가 공정하게 기여할 수 있도록 하였다고 합니다. 즉, 모달리티 간의 균형적인 학습을 통해 멀티모달 모델의 전체 성능을 향상시키고자 한 것입니다.

또한, mono-modal이라는 개념을 도입하여 modality competition이 없을 때 각 모달리티가 어떻게 독립적으로 동작하는지를 정의하고, 이를 기반으로 competition strength를 직접 측정하는 새로운 metric을 제안하였습니다. 해당 metric을 통해 멀티모달 모델에서 각 모달리티 간의 competition strength를 정량적으로 평가하고, AGM의 효과를 분석하였는데, 이는 아래에서 설명드리도록 하겠습니다.

Method

Adaptive Gradient Modulation (AGM)

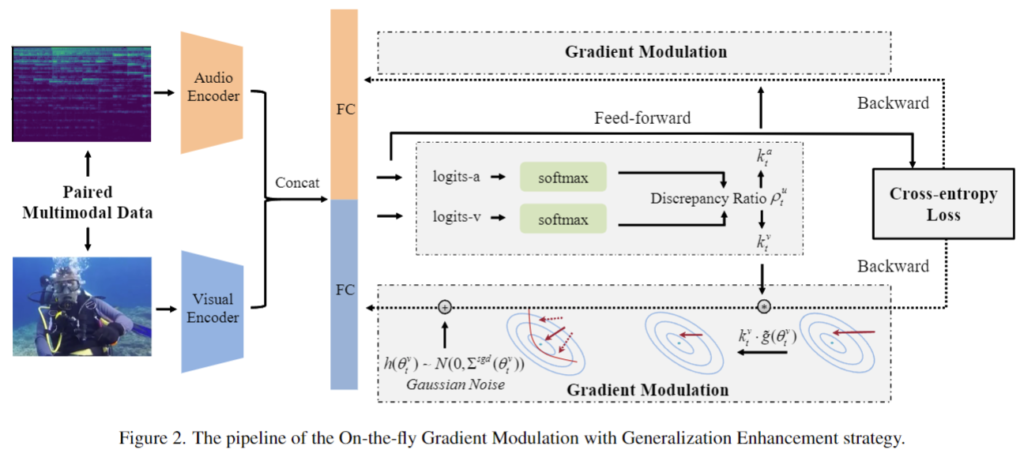
논문의 저자들이 제안하는 AGM은 OGM-GE 알고리즘에 영감을 받았다고 하는데요, OGM-GE는 제가 이전에 리뷰했던 [CVPR 2022] Balanced Multimodal Learning via On-the-fly Gradient Modulation 논문에서 제안되었으며, 위의 그림과 같이 멀티모달 모델에서 각 단일 모달의 학습 정도인 discrepancy ratio를 측정하여 gradient에 가중치를 부여하는 식으로 여러 모달리티간의 imbalance problem을 해결하는 방법론이었습니다. 그러나 OGM-GE는 late fusion 방식에서만 활용이 가능하고, 두 가지의 모달리티만을 고려할 수 있다는 한계점이 있었는데요, 이를 해결하기 위해 저자들은 아래와 같은 새로운 방법론인 AGM을 제안하였습니다.

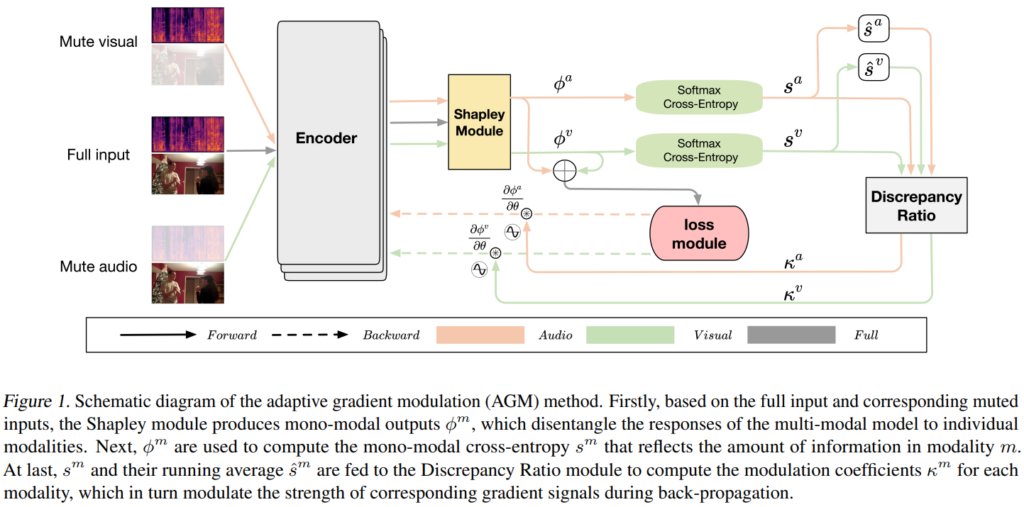
위의 [그림 1]이 저자들이 제안하는 Adaptive Gradiant Modulation(AGM)으로, OGM-GE와 마찬가지로 discrepancy ratio를 통해 단일 모달리티 각각의 학습 참여도를 조절하는 방식으로 동작합니다.

저자들은 AGM과 OGM-GE의 차이점을 세 가지로 언급하였습니다. 먼저 단일 모달의 response를 계산하기 위해 Shapley value-based attribution method를 사용하여 late fusion 방식에 국한되지 않고 다양한 fusion method에서도 원활히 동작할 수 있도록 하였다고 합니다. 다음으로는 두 가지 이상의 모달리티를 사용하는 상황에서 discrepancy ratio를 계산하는 방식을 정의하였습니다. 마지막으로는 discrepancy ratio를 1이 아닌 running average로 조절함으로써 서로 다른 모달리티 간의 차이를 반영하였다고 합니다.

Isolating the mono-modal responses

AGM의 핵심 기능 중 하나는 단일 모달리티의 response를 파악하는 것인데요, 여기서 modality response란 특정 모달리티가 멀티모달 시스템 내에서 어떻게 반응하고 데이터를 처리하는 지를 의미합니다. 즉, 각 모달리티가 멀티모달 출력에 어느 정도로 기여하는 지를 파악하는 것이라고 이해하시면 될 것 같습니다.

먼저 nonation에 대해 설명드리겠습니다. ϕ(x)는 k개의 모달리티를 가지는 입력 데이터 x = (x^{m_1}, ..., x^{m_k})에 대한 멀티모달 모델이며, M := {m_i}_{i \in [k]}은 모든 모달리티의 집합을 의미합니다. 0^m은 어떤 모달리티 m이 특성이 없음, 즉 모두 0임을 나타냅니다. S가 M의 부분집합일 때, ϕ(S)는 m이 S에 포함될 경우, 구성요소 x^m이 0^m으로 대체된다는 것을 의미합니다.

이때, 모달리티 m에 대한 단일 모달 response는 아래 [수식 1]과 같이 정의됩니다.

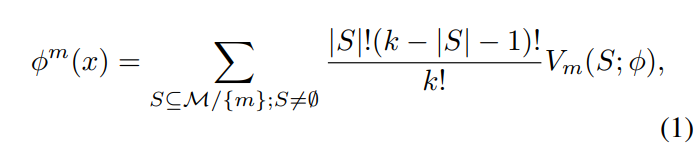
[수식 1]에서 Vm(S; ϕ)은 ϕ(S ∪ {m}) − ϕ(S)를 의미하며, 이는 s와 s가 아닌 모달리티를 함께 사용하여 예측한 것과 s만을 사용하여 예측한 값의 차를 나타냅니다.

위의 수식을 통해 구한 각 모달리티의 response는 아래의 아래 [수식 2]를 만족하게 됩니다.

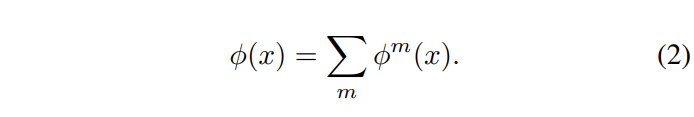
[수식 1]을 2가지 모달리티 (m1, m2)에 대해 일반화를 진행하면, 위의 [수식 1]은 아래 [수식 3]과 같이 정리될 수 있습니다.

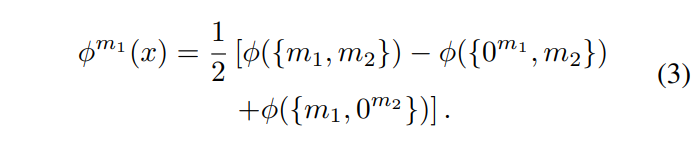
어떠한 모달리티의 response를 구했다면, 해당 모달리티의 단일 모달 cross entropy s^m 와 accuracy를 구할 수 있는데요, 이는 각각 아래 [수식 4]와 [수식 5]와 같이 구할 수 있습니다.

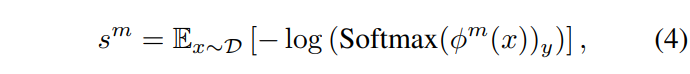
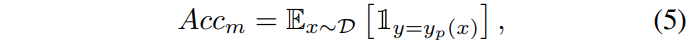
Modulating the training process

앞서 AGM은 각 모달리티의 gradient를 조절하는 방법이라고 언급하였는데요, AGM에서는 모델의 파라미터를 업데이트할 때 아래 [수식 6]과 같이 gradent의 강도를 조절하였습니다.

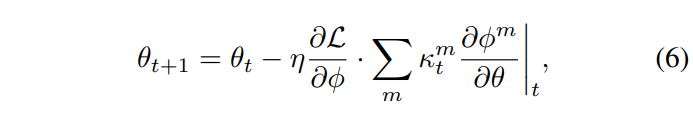
[수식 6]에서 t 는 학습 iteration을 나타내며, \theta 는 learnable parameter를, \eta 는 learning rate, L 은 Loss입니다.

위 수식에서 learning rate \eta 와는 별개로 계수 \kappa^m_t 가 t 에서 모달리티 m 의 gradient를 조절하는 것을 볼 수 있는데, 이는 어떤 모달리티가 너무 강하거나 약한 경우 해당 모달리티의 업데이트를 억제 혹은 증폭하는 역할을 수행한다고 이해하시면 될 것 같습니다.

어떠한 모달리티의 강도는 다른 모달리티와의 상대적인 차이의 평균값으로 측정하였으며, 어떤 모달리티 m의 강도 r은 아래 [수식 7]과 같이 m을 제외한 다른 모달리티와 [수식 4]의 단일 모달 CrossEntropy의 차이를 더한 값으로 구할 수 있습니다.

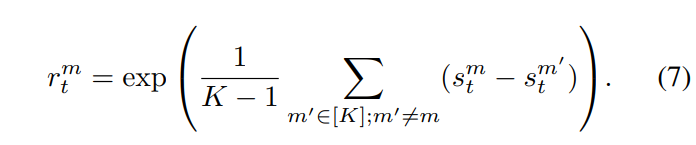
그런 다음 \kappa^m_t 는 아래 [수식 8]과 같이 구할 수 있습니다.

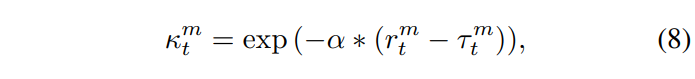
여기서 \alpha > 0 은 하이퍼파라미터이며, \tau^m_t 는 reference 값입니다. reference 값을 통해 kappa 값을 조절할 수 있는데요, 모달리티가 강할 때 즉, (r^m_t > \tau^m_t) 인 경우에 (\kappa^m_t < 1) 을 만족하게 되어 [수식 6]에서 더 작은 step으로 파라미터를 업데이트하게 됩니다.

\tau^m_t 는 아래의 [수식 9]와 같이 계산하며, \hat{s}^m(t) 는 [수식 10과 같이 t 에서의 단일 모달 Cross entropy의 running average로 [수식 10]과 같이 설정하였습니다.

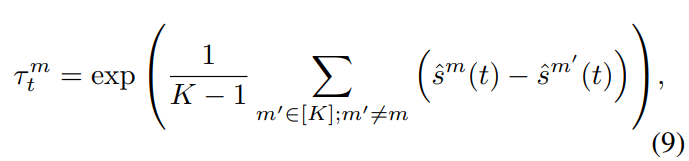
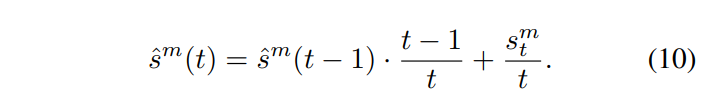
Mono-modal competition strength

논문에서는 멀티모달 내에서 각 단일 모달의 독립적인 영향력을 기반으로 멀티모달 모델이 competition-less한 상황과 얼마나 차이가 있는지, 즉, 멀티모달 내의 competition 정도를 정량적으로 측정하고자 하였습니다. Competition-less 한 상황에서 멀티모달 모델의 response의 편차를 추정하기 위해 저자들은 Linear probing method를 사용하였습니다. 구체적으로 설명드리자면, 멀티모달 모델의 마지막 FC층 이전의 latent feature를 z 라고 할 때, z 에서 mono-modal model concept C^m 으로의 linear classifier를 학습하였습니다. 이를 수식으로는 아래와 같이 나타낼 수 있습니다.

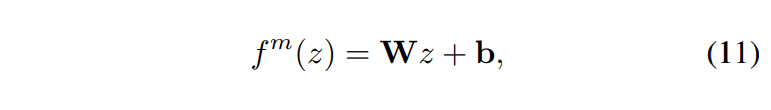
해당 모델의 파라미터 W 와 b 는 [수식 12]와 같이 예측값의 MSE를 최소화함으로써 결정됩니다.

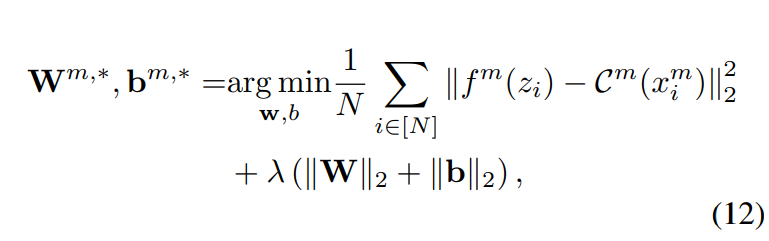
여기서 \|\cdot\|_p 는 L_p norm을 나타내고, i 는 데이터 sample의 index를 의미하며, \lambda 는 regularization strength입니다. L_2 regularization은 과적합을 피하기 위해 사용하였다고 합니다.

위의 linaer fitting의 quality는 멀티모달 feature가 competition-less한 상태에서 얼마나 벗어났는지를 반영하게 되므로, 최종적인 competition strength는 아래의 [수식 13]과 같이 정의하였다고 합니다.

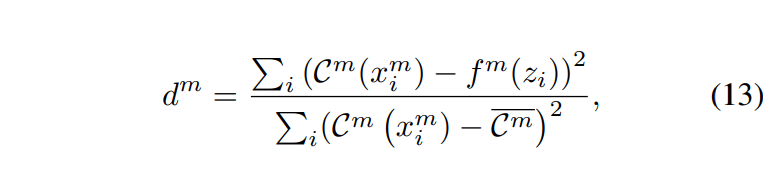
여기서 \overline{C^m} 은 데이터 샘플에 대한 평균 mono-modal concept 값이며, d^m 은 평균 값을 예측하는 linear prediction의 quality를 측정하게 되는데, 0에서 1까지의 범위를 가지며 1에 가까워질수록 강한 competition level을 가지는 것을 의미합니다.

Experiments

The effectiveness of AGM

[표 1]부터 [표 3]은 동일한 실험을 각각 AV-MNIST, UR-Funny, CREMA-D에서 진행한 결과입니다. 실험은 멀티모달의 여러 fusion strategy들을 비교함으로써 AGM의 우수성을 증명하고자 하였으며 이때 각 모달리티의 인코더는 resnet18 혹은 transformer를 사용하였다고 합니다.

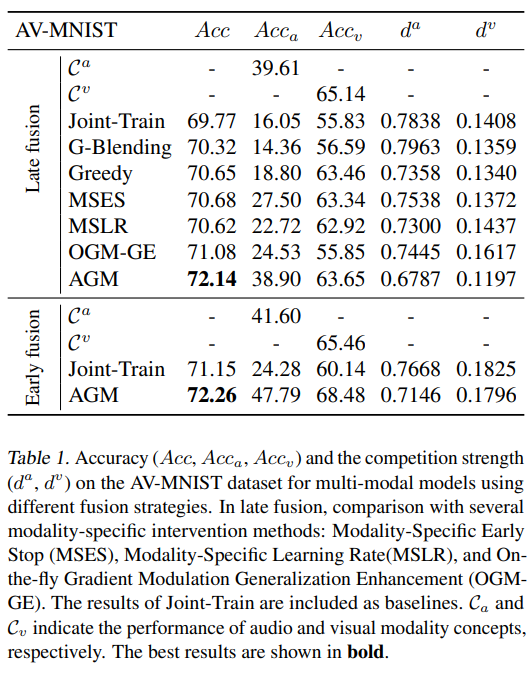
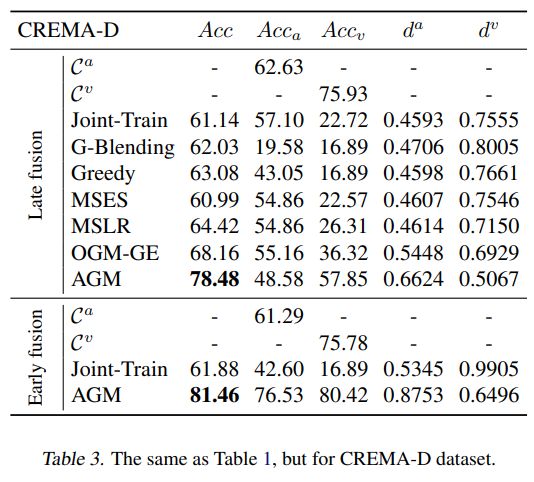
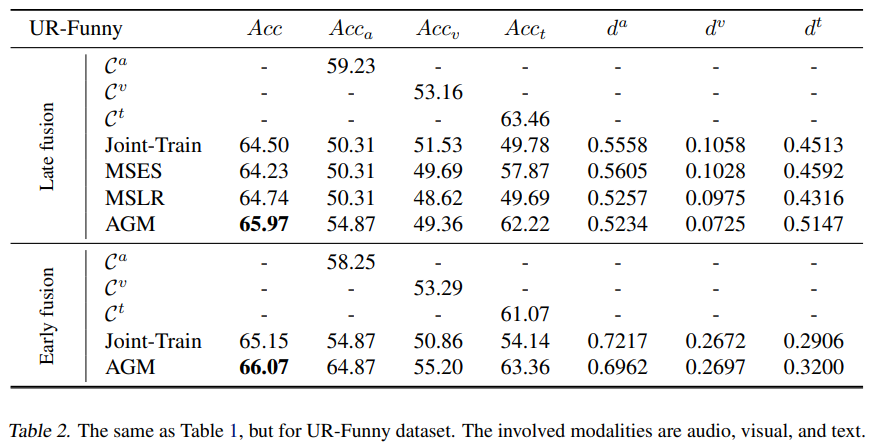
AV-MNIST, UR-Funny, CREMA-D모두 AGM을 적용하였을 때 가장 높은 정확도를 보인 것을 확인할 수 있습니다. 논문에서는 late fusion에만 적용 가능했던 기존 fusion 방법들과는 달리 AGM은 early fusion에도 적용 가능하다는 것을 강조하였습니다.

AGM은 특히 CREMA-D에서 큰 성능 향상을 가져왔는데요, [표 3]을 보면 기존에 가장 성능이 높았던 OGM-GE와 AGM의 성능 차가 10.34%임을 확인할 수 있습니다. 이러한 성능 향상의 이유를 논문에서는 CREMA-D 데이터셋에서 가장 정보가 많은 모달리티인 visual 모달리티가 joint training에서 충분히 활용되지 않았기 때문이라고 하는데요, 단일 visual 모달리티는 단일 audio보다 높은 75.93%의 정확도를 보이나, joint training에서 visual 모달리티의 mono-modal accuracy는 22.72%에 불과한 것을 확인할 수 있습니다.