[CVPR 2023] PointConvFormer: Revenge of the Point-based Convolution

안녕하세요, 스물 다섯 번째 x-review 입니다. 이번 논문은 2023년도 CVPR에 게재된 PointConvFormer: Revenge of the Point-based Convolution으로, 지난 주에 읽은 PointConv의 후속작 입니다. 그럼 바로 리뷰 시작하겠습니다 !

1. Introduction

indoor/outdoor 환경에서 3차원 정보를 제공하는 depth 센서는 로보틱스 분야를 비롯한 여러 분야에서 유용하게 사용되고 있습니다. 그러나 일정한 그리드로 나뉠 수 있는 이미지 픽셀과 다르게 depth 센서로 취득하는 포인트 클라우드는 균일하지 않은 형태로 주어지기 때문에 일반적인 CNN에서의 계산이 어렵습니다. 그래서 이러한 문제를 해결하기 위해서 여러 방향으로 연구가 진행되고 있는데요, 먼저 포인트 클라우드를 이미지 공간으로 사영하여 2D convolution을 적용할 수 있습니다. 혹은 raw한 포인트 클라우드를 복셀 형태로 변형하여 3D discrete convolution을 적용하는데, 이는 많은 계산, 메모리 비용을 요구합니다. 그래서 많은 방법론이 sparse한 포인트 클라우드가 포함되어 있는 복셀 그리드만 계산의 입력으로 넣을 수 있는 sparse 3D convolution을 사용하여 계산 비용을 줄이면서 3차원 포인트 클라우드를 2차원 평면으로 옮기지 않고 연산하고 있습니다. 또는 raw한 포인트 클라우드를 그대로 입력으로 사용하거나, 포인트 클라우드를 convolution 동작에 직접적으로 사용하기 위한 연구가 진행되고 있습니다. 전자의 경우 PointNet++을 백본 네트워크로 사용하여 복셀화 시키지 않고 포인트 클라우드를 입력 데이터로 사용하며 후자는 포인트 클라우드 간의 로컬한 이웃 포인트로 그룹을 만들어 MLP를 이용해서 그룹 내에서 상대적인 위치 정보로부터 nonlinear transformation하여 convolution 가중치를 학습합니다. 본 논문에서는 후자의 경우인 포인트 클라우드를 직접적으로 convolution 연산에 활용하는 관점으로 접근하고 있는데, 그 이유는 포인트 클라우드를 직접 처리하는 방식이 포인트의 좌표를 가공 할 수 있어서 회전/스케일 invariance/equivariance를 convolution 가중치에 직접 인코딩할 수 있기 때문이라고 합니다. 이러한 invariance는 모델의 일반성을 높이며 포인트 기반의 접근 방식은 3D convolution을 사용하여 3x3x3 컨볼루션 커널을 유지해야하는 복셀 기반에 비해 훨씬 더 적은 파라미터로 학습이 가능합니다. 또한 입력으로 포인트 클라우드를 직접 넣게 되면 KNN과 같이 이웃 포인트를 찾기 위한 알고리즘을 사용할 수 있는데, 이는 3차원 위치에 대해서 다양한 샘플링이 가능하다는 장점이 존재합니다. 위와 같은 장점이 존재하지만, 현재까지 정확도와 속도의 trade off 관계를 고려하였을 때 가장 성능이 좋은 방법론은 여전히 sparse 복셀 기반 혹은 sparse 복셀과 포인트 기반 모델을 fusion한 방식이라고 합니다. 그러나 저자는 복셀 기반이나 포인트 기반이나 representation에 있어서 입력 정보는 정확히 동일하며, 더불어 fusion은 모델 복잡도와 상당한 메모리 사용을 요구하기 때문에 fusion이 필요한 이유가 뚜렷하지 않다고 주장합니다. 그래서 근본적으로 두 방법론의 representation에서 다른 점이 무엇인지 분석하여 불균일한 포인트 클라우드의 로컬한 이웃을 찾는다는 점에서 차이를 발견하였습니다. 포인트 기반에서 KNN 알고리즘의 결과로 나오는 shape은 전체 포인트 클라우드에서 다양하게 나타날 수 있습니다. 이러한 하나의 중심 포인트에 대한 이웃 포인트로 이루어진 포인트 영역의 단위를 보통 한 개의 그룹이라고 정의합니다. 그룹을 정의하는 이유는 하나의 그룹을 물체일 후보라고 가정하는데요, 이러한 그룹은 물론 동일한 물체를 나타낼 수도 있지만 배경이나 다른 물체를 나타내는 일명 노이즈한 포인트가 포함될 수도 있습니다. 노이즈한 포인트를 최대한 포함시키지 않는 그룹을 만들수록 물체를 더 정확하게 검출할 수 있겠죠. KNN 알고리증믈 사용하면서 모델의 성능을 향상시키기 위해 feature correlation이 높은 포인트들을 같은 이웃에 포함되어야 한다는 CNN의 일반화 이론에 집중하게 됩니다. 그래서 본 논문의 핵심 아이디어는 feature correltation이 KNN으로 뽑은 이웃 포인트에서 노이즈 포인트를 필터링하는 방법이며, 이를 통해 subsequent convolution을 보다 일반화시킬 수 있다는 것 입니다.

그래서 본 논문은 feature의 차이에 따라 attention 가중치를 계산하고 이를 사용하여 포인트 기반의 convolution 모델에서 이웃 포인트마다 서로 다른 가중치를 부여해서 이웃 포인트의 퀄리티를 간접적으로 개선할 수 있는 PointConvFormer을 제안합니다. feature 기반의 attention을 새롭게 제안하지는 않았지만 PointConvFormer와 다른 ViT에는 차이가 존재한다고 합니다. 트랜스포머 attention 모델은 일반적으로 소프트맥스 attention 방식을 사용하는 반면, 이웃의 feature을 point-wise-convolution과 결합합니다. 또한 위치 정보가 attention 모듈에 사용되지 않기 때문에 convolution 가중치에 viewpoint-invariance를 고려할 수 있습니다. 이러한 invariance를 고려하면 train/test 데이터셋 간의 이웃 포인트 형태(크기/회전)에 대한 차이를 일반화하는데 도움이 된다고 합니다.

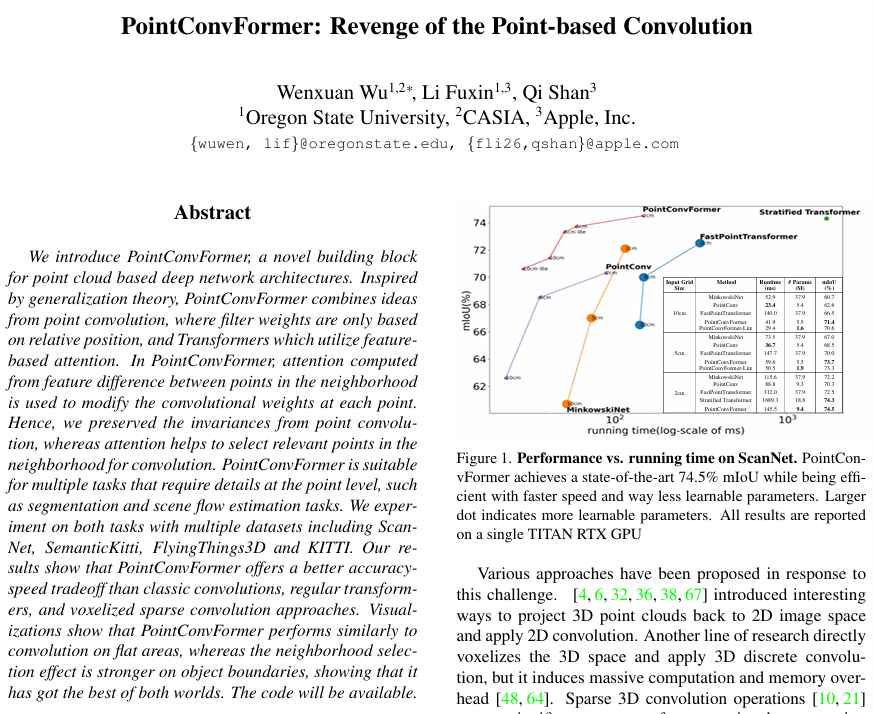
PointConvFormer을 검증하기 위해 두 포인트 클라우드를 사용하는 task인 semantic segmentation과 scene flow estimation 실험을 진행하였습니다. semantic segmentation에서는 일반적인 convolution과 트랜스포머 구조에서 훨씬 간단한 네트워크로 우수한 성능을 보였으며 scene flow estimation에서는 PointConvFormer을 기존 모델 구조의 백본과 교체하여 큰 폭의 성능 향상을 보였다고 합니다. 이러한 실험 결과를 통해 PointConvForemr가 3차원 인지 task에서 sparse 3D convolution을 대체하여 사용할 수 있는 backbone임을 보여준다고 합니다.

2. PointConvFormer

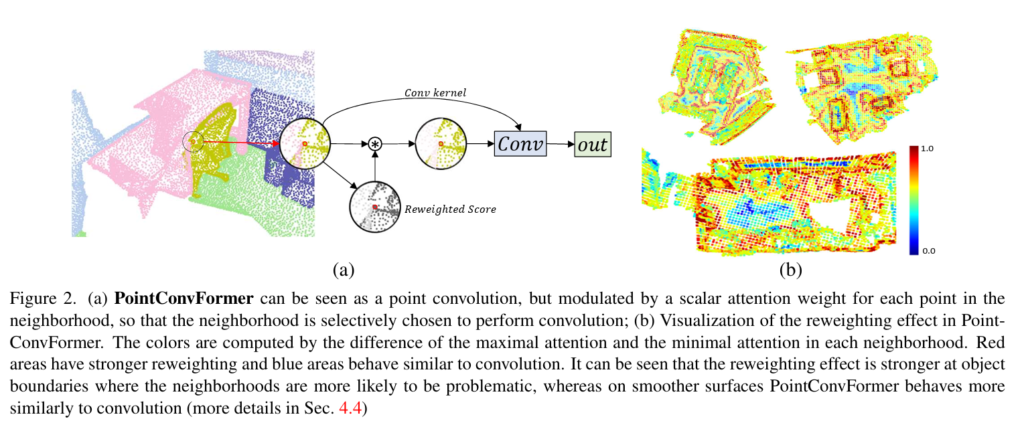
2.1. Point Convolutions and Transformers

연속적인 입력 p \in \mathbb{R}^s의 x(p) \in \mathbb{R}^{c_{in}}가 들어오면 (여기서 s는 포인트 클라우드에 대한 3차원), x(\cdot)은 포인크 클라우드 P = \{p_1, . . ., p_n\}으로 정의할 수 있고 그에 대응하는 x_P \{x(p_1), . . . , x(p_n)\}이 됩니다. 즉 P는 포인트 클라우드를 의미하고, x_P는 그에 매칭되는 3차원 좌표를 의미하겠죠.

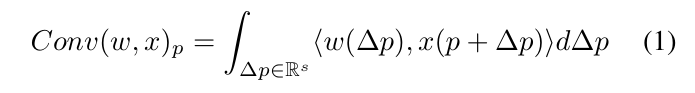
• w(\vartriangle p) \in \mathbb{R}^{c_{in}} : convolution 가중치 함수

각 포인트 p에서의 연속적인 convolution은 식(1)과 같이 정의할 수 있습니다. PointConv에서는 여기서 포인트 p의 이웃 포인트에 대한 연속적인 convolution을 이산화하게 되는데, 포인트에 대한 이산화된 convolution은 아래 식(2)와 같이 정의합니다.

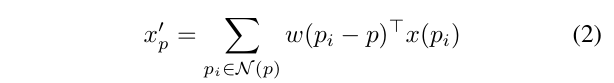
• \mathcal{N}(p) : 중심 포인트 p에 대해 KNN, \epsilon-ball 알고리즘으로 형성한 이웃

w(p_i - p) : \mathbb{R}^s \mapsto \mathbb{R}^{c_{in}}은 MLP로 근사화하여 학습할 수 있습니다. 또한 p_i - p는 이웃을 형성한 하나의 그룹 내에서 컨트롤할 수 있기 때문에 회전 불변인 좌표 변환을 w(\cdot)의 입력으로 포함할 수 있습니다. 이미 이전 연구에서 회전 및 스케일 불변한 좌표 변환 집합을 포함하는 것이 포인트 기반 convolution의 성능을 크게 향상시킴을 증명하였다고 합니다.

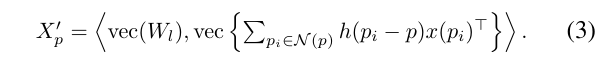
• h(p_i - p) : \mathbb{R}^3 \mapsto \mathbb{R}^{c_{mid}}, MLP의 fc 레이어의 출력
• W_l : W_l \in \mathbb{R}^{c_{in} \times c_{mid}}, 마지막 linear layer의 파라미터

PointConv에서는 마지막 linear layer의 w(p_i - p)가 W_lh(p_i - p)일 때 가장 효율적인 네트워크를 구축할 수 있으며 이를 식(3)과 같이 정의하였습니다.

W_l은 linear layer의 파라미터를 나타내기 때문에 p_i와 상관관계가 없습니다. 즉, convolution 커널 c_{out}와 각 이웃 포인트의 크기가 k 일 때, 이웃 포인트에 대해서 원래 convolution 가중치 w(p_i - p)를 c_{out} \times c_{in} \times k \times n의 차원으로 저장할 필요가 없어집니다. 모든 h(p_i - p) 벡터의 차원은 c_{mid} \times k \times n에 불과한 수준으로, 여기서 c_{mid}는 일반적으로 104보다 더 높은 값을 가질 수 있는 c_{out} \times c_{in}보다 훨씬 작은 4에서 16사이의 값을 가지게 됩니다.

이러한 효율적인 PointConv 네트워크는 large scale의 네트워크에서 포인트 클라우드를 처리할 수 있도록 하였습니다. 게다가 가장 cost가 많이 드는 W_l(\cdot)에서 c_{mid} \times c_{in} \times c_{out} 파라미터를 사용하면서(c_{mid}는 보통 4 정도의 값을 가진다고 합니다) 27 \times c_{in} \times c_{out}개의 파라미터를 요구하는 일반적인 sparse 3D convolution 대비 훨씬 작은 사이즈의 모델을 설계합니다.

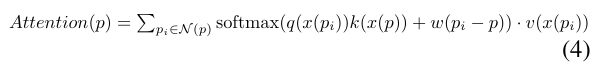
현재 트랜스포머는 두 포인트의 feature와 position 인코딩을 기반으로 포인트 간의 attention 계산을 합니다. 전체 포인트에 대한 절대적인 위치보다 상대적인 위치에 대한 인코딩이 더 나은 성능을 보이며 많이 사용되고 있습니다. 상대적인 position encoding은 w(p_i - p)를 인코딩하며 식(2)과 유사합니다. 이러한 트랜스포머에서 사용되는 softmax attention 모델은 식(4)와 같이 정의합니다. 식(4)에서 q(\cdot), k(\cdot), v(\cdot)는 각각 query, key, valu를 형성하기 위한 feature 변환으로, 일반적으로 MLP로 구현됩니다. PointConv와 attention을 비교해보면, 모두 w(p_i - p)를 사용한다는 점은 동일하지만, PointConv에서는 translation invariant한 convolution 커널의 유일한 소스로 사용하는 반면 attention에서는 query transform q(x(p_i))와 feature의 key transform k(x(p)) 사이의 매칭을 추가적으로 고려합니다. 또한 attention 모듈에 h(p_i-p)가 포함되지 않으면 PointConv가 스케일과 회전과 같이 invariant 좌표 변환을 활용할 수 있어 더욱 강인하게 작동이 가능합니다. 트랜스포머는 일반적으로 attention 모듈 뒤에 fc layer 2개를 사용하는데, 이는 h(\cdot)과 W(\cdot)과 유사한 구조를 이룹니다. 심지어 트랜스포머의 첫번째 fc layer는 4\times의 차원으로 확장되는데, 이는 PointConv에서 c_{mid}와도 유사성을 띄고 있네요. 이러한 점을 보아 전체 트랜스포머 모델은 PointConv와 유사한 점을 확인할 수 있지만 가중치를 생성하는 과정에서 x(p) feature가 활용된다는 차이가 있습니다. 그러나 한 가지 고려할 점은 식(3)에서 h(p_i - p)는 단일 헤드만 사용하는 경우 식(4)에 존재하지 않는 c_{mid} > 1을 갖는 p_i - p의 nonlinear transform 집합을 만들게 됩니다. 즉, 식(4)를 사용하면 입력 feature의 nonnegative한 값만을 만들 수 있다는 것 입니다. 트랜스포머에서는 멀티헤드가 서로 다른 v(\cdot)을 사용하여 이웃 포인트의 negative 값 사용을 가능하게 합니다. 이러한 구조는 각 이웃 포인트의 positive 와 negative를 모두 사용할 수 있게 하여 서로 다른 h(\cdot)를 W_l과 결합하는 PointConv에서는 불필요하여 생략 가능합니다.

2.2. CNN Generalization Theory and The Point-ConvFormer Layer

이제 본격적으로 PointConvFormer 모델에 대해서 살펴볼건데, 본 논문에서는 convolution의 구조를 유지하면서 attention 기반 모델의 negative 가중치를 가지는 특징을 어떻게 가져올 지에 집중하였습니다. 이를 위해 먼저 일반화가 잘 이루어질 수 있는 구조에 대한 분석을 진행하였고, 앞선 연구에서 증명된 식(5)에 집중하였다고 합니다.

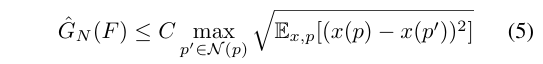
• \hat{G}_N(F) : 함수 F에 대한 경험적 가우시안 복잡도

이전 연구를 통해서 가우시안 복잡도가 작을수록 일반화가 더 잘 이루어진다는 점이 증명되었으며 식(5)의 바운드를 최소화하기 위해서는 같은 그룹에서 feature correlation이 높은 포인트를 선택해야 합니다. 가령 이미지에서는 가까운 픽셀은 일반적으로 컬러 correlation이 가장 높기 때문에 기존 CNN은 작은 로컬 범위로 이웃을 선택함으로써 ( ex. 3×3 커널 ) 더 나은 일반화를 달성하고자 하였습니다. 비록 이러한 바운드가 트랜스포머 모델에 직접적으로 적용되지는 않지만, attention을 이용하여 correlation이 낮은 이웃 포인트를 제외한다는 컨셉은 CNN에서 식(5)의 일반화 바운드를 직접적으로 개선할 수 있습니다. 앞서 계속 이야기하였듯 3차원 포인트 클라우드에서 노이즈로 정의되는 포인트가 KNN을 통해 이웃에 포함될 수 있다는 가정이 노이즈 포인트의 x(p) - x(p’)를 명식적으로 확인하고 필터링하여 그룹 내에서 동일한 물체로 간주되는 포인트만 이웃에 포함하는 컨셉에 모티브가 되었습니다. 이에 저자는 상대적인 위치 p_i - p와 두 포인트에 대한 feature 차이 x(p_i) - x(p)를 모두 고려하는 새로운 convolution 연산인 PointConvFormer을 정의합니다. 점 p와 해당하는 이웃 \mathcal{N}(p)의 PointConvFormer 레이어는 식(6)과 같이 정의할 수 있습니다.

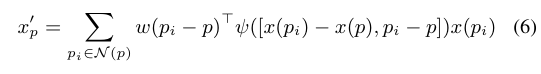
• w(p_i - p) : 식(2)와 동일
• \psi([x(p_i) - x(p), p_i - p]) : feature 차이 X_{pi} - X_p와 위치 좌표 차이에 대한 함수

실제로 \psi(\cdot)은 활성화 함수 뒤로 이어지는 MLP로 근사화됩니다. \psi(\cdot) 1로 고정하면 PointConvFormer는 식(2)와 동일하게 기존 convolution으로 간주됩니다. PointConvFormer에서 w(p_i - p)는 상대적인 위치에 대한 가중치를 학습하고, \psi(\cdot)는 이웃에서 유의미한 포인트를 선택하는 방법을 학습하는데, 이는 트랜스포머의 attention과 유사하게 작동합니다. 그러나 negative가 아닌 가중치가 입력에 가중합으로 직접 사용되는 트랜스포머와는 달리, \psi(\cdot)의 출력값은 convolution 필터 w(p_i - p)만 수정하여 각 이웃 포인트가 positive와 negative에 모두 영향을 받도록 합니다. 따라서 w(p_i - p)를 \psi(\cdot) 함수에 포함시키지 않으면 invariance를 인식하는 position encodig의 이점을 최대한 활용할 수 있습니다.

3.3. PointConvForemr Block

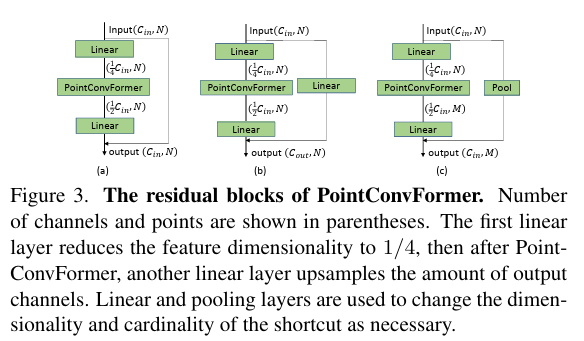
실제 task들에 사용할 수 있는 신경망 구조를 구축하기 위해서 PointConvFormer 레이어를 메인으로 하는 bottleneck residual block을 설계합니다. Fig 3이 residual block에 대한 자세한 구조로, residual block은 두 개의 브랜치로 구성된 bottleneck 구조를 사용합니다. 입력은 포인트 클라우드의 좌표 p \in \mathbb{R}^3과 포인트 feature X \in \mathbb{R}^{c_{in}}이 들어가게 됩니다. 메인 브랜치는 하나의 linear layer로, 이어서 PointConvFormer 레이어, 또 다른 linear layer로 이어집니다. 맨 앞의 linear layer에서 입력 채널의 1/4로 줄어들고, 더 적은 수의 채널로 PointConvForemr을 통과한 다음 마지막으로 출력 채널 수까지 업샘플링함으로써 모델 크기와 계산 비용을 크게 줄이면서 PointConv와 PointConvFormer 두 모델 모두에서 높은 정확도를 유지할 수 있습니다.

3. Experiments

실험은 포인트 클라우드를 사용하는 두 개의 task, 3D semantic segmentation과 scene flow estimation에서 진행하였습니다. 먼저 3D semantic segmentation에는 indoor 데이터셋인 ScanNet과 outdoor 데이터셋인 SemanticKitti을 사용하였습니다. scene flow estiation에서는 합성 데이터셋인 FlyingThings3D와 KITTI 데이터셋을 사용하였네요.

3.1. Indoor Scene Semantic Segmentation

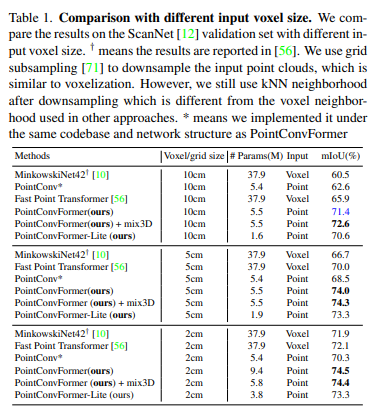
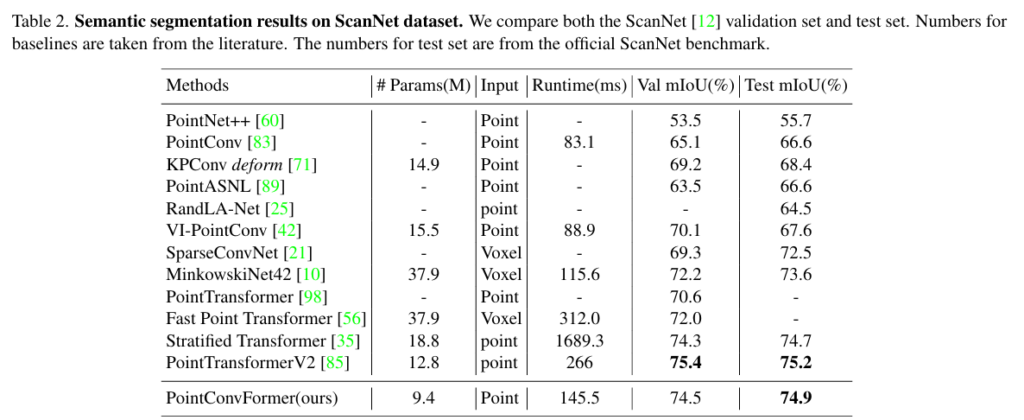
먼저 ScanNet에서 복셀 기반의 MinkowskiNet42와 SparseConvNet 그리고 포인트 기반의 여러 방법론과의 semantic segmentation 결과를 비교하였습니다. 복셀 기반에 대해서는 Table1과 같이 여러 복셀 그리드 사이즈를 설정하여 실험을 진행하였다고 하네요. 또한 트랜스포머를 사용하는 PointTransformer과 Fast Point Transformer을 비교 모델로 삼았다고 합니다. PointTransformer는 ScanNet 데이터셋에 대한 결과를 리포팅하지 않기 때문에 동일한 네트워크 구조를 가진 본 논문과 동일한 네트워크 구조를 가진 PointTrnasformer 레이어 ( 멀티 헤드 어텐션 레이어 )를 가지고 와서 실험을 진행하였습니다. 즉, PointConvFormer와 멀티 헤드 어텐션을 직접 비교할 수 있는 비교 대상을 선정하였습니다.

Table1과 Table2를 동시에 보면, 입력 그리드 사이즈에 관계없이 PointConvForemr가 정확도와 속도의 트레이드 오프가 가장 뛰어난 것을 확인할 수 잇습니다. 그 중 복셀 그리드 사이즈 2cm일 때는 940만개의 파라미터를 사용하는 mix3D 모델보다 성능 개선을 이루지는 못하였지만, 580만개의 파라미터를 가진 훨씬 작은 모델로 비슷한 성능을 달성하였다는 점에서 의미있다고 분석하고 있습니다. 또한 본 논문에서는 더 적은 레이어를 사용하는 경량화 버전인 PointConvFormer-Lite를 추가적으로 제안하는데, 성능 저하를 최소화하면서 더 빠르고 높은 메모리 효율을 가진다고 합니다.

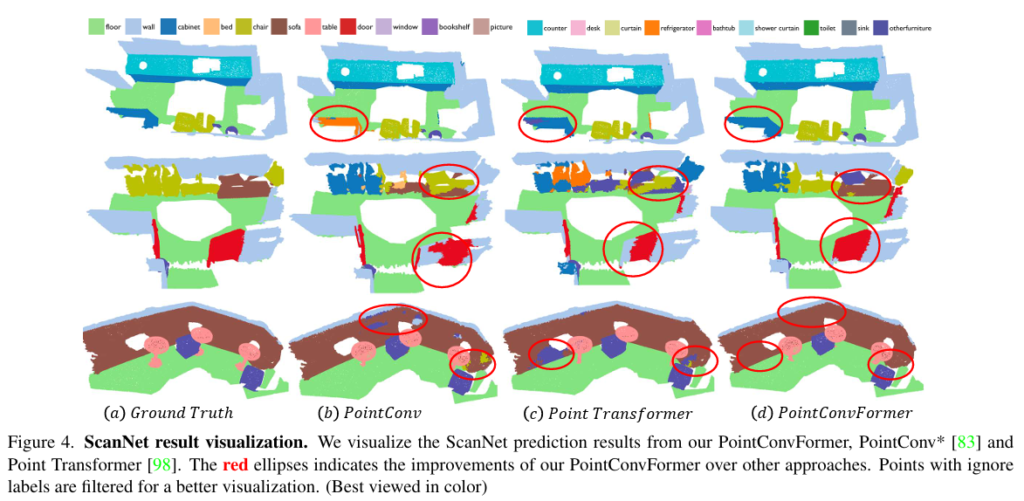
Figure 4는 ScanNet 데이터셋에서 세 모델을 비교한 정성적 자료로, PointConvForemr가 PointConv와 PointTransformer에 비해 더 정확하게 기존 물체를 예측하고 있는 것을 확인할 수 있습니다. 이러한 결과의 이유로 저자는PointConvForemr가 CNN과 트랜스포머의 장점을 복합적으로 활용하고 있기 때문이라고 이야기합니다.

3.2. Outdoor Scene Semantic Segmentation

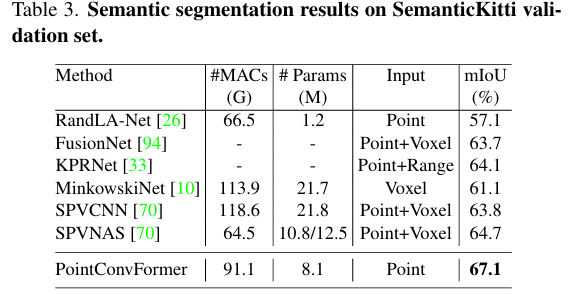
outdoor 데이터셋으로 SemanticKitti를 사용한 이유는 모든 종류의 3차원 포인트 클라우드 데이터에 적용할 수 있는 신경망 구조로 PointConvFormer을 제안하였기 때문에 LiDAR로 스캔하여 BEV로 변환하는 방법론들과의 비교는 배제하였다고 합니다. Table3이 outdoor 데이터셋에서의 실험 결과로, 포인트 기반 방법론과 복셀,포인트 fusion 방법론 모두에서 PointConvFormer가 더 높은 성능을 보이고 있습니다.

3.3. Scene Flow Estimation from Point Clouds

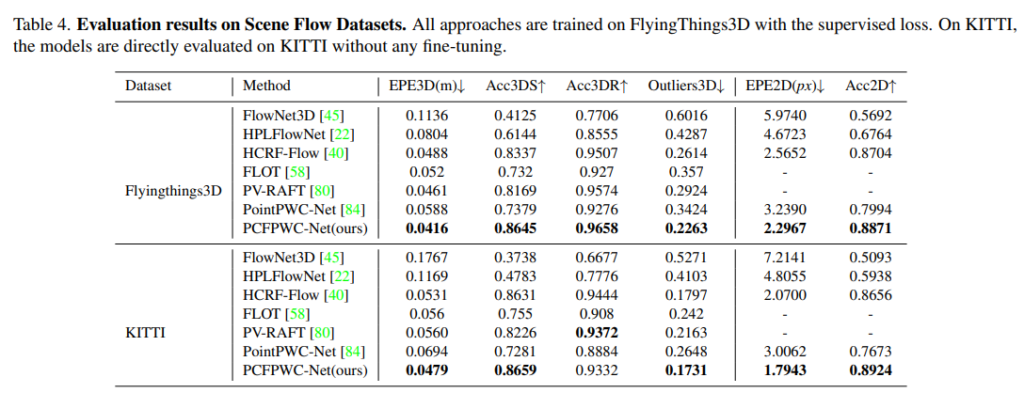
일반적으로 scene flow는 RGB 데이터에서 추정되는데, 최근 라이다와 같은 3차원 센서로 포인트 클라우드에서 scene flow를 추정하는 연구가 활발히 진행된다고 합니다. 본 연구에서는 scene flow estimation을 위해 coarse-fine 프레임워크를 활용하는 PointPWC-Net에서 FPN 구조의 PointConv를 PointConvFormer 레이어로 대체하고 나머지 구조는 기존의 PointPWC-Net과 동일하게 유지하여PointConvFormer을 scene flow estimation에서 실험할 수 있는 구조로 변형하였습니다. 이러한 구조가 Table4에서 PCFPWc-Net(ours)라고 표시된 모델 입니다. 기존 PointPWC-Net과 비교하여 ours는 약 10%의 성능 향상을 모든 메트릭에서 달성하였습니다. 또한 KITTI 데이터셋에서는 EPE3D의 0.0694 대비 0.0479의 성능을 보이며 무려 30% 이상의 성능 개선을 이루었습니다.