안녕하세요! 이번에도 multimodal 관련 논문을 들고 왔는데요. 제목이 굉장히 흥미가 돋지 않습니까? 그래서 리뷰하고자 하였습니다. 그럼 리뷰 시작합니다!

<Abstract>

본 논문에서는 multimodal 성능이 un-modal 성능에 비해서 낮게 나오는 점이 발견되었고, 실제로 이러한 현상은 다양한 모달리티 조합에서 발생하며 video classification 및 다른 task 벤치마크에서 일관되게 나타났음을 말합니다.

논문의 저자는 이러한 현상이 나타나는 이유를 두 가지로 분류하여 설명하는데요. 첫 번째는 uni-modal에서 multi-modal network로 확장하는 과정에서 모델의 용량 증가로 인해 과적합이 발생하기 쉽기 때문이라고 합니다. 두 번째는 서로 다른 모달리티는 서로 다른 속도로 과적합하고 일반화한다는 점 때문인데요. 이 때문에 multi-modal network가 단일 최적화 전략으로 학습이 된다면 여러 모달리티의 최적화 속도 차이로 인해서 최적화가 힘들다는 것이죠.

그래서 본 논문의 저자는 gradient blending을 통해서 해결해보고자 하였습니다.

<Introduction>

abstract에서 말씀드린데로, mult-modal에 비해서 uni-modal의 성능이 높은 경우가 있습니다. 왜 그런걸까요? multimodal network의 성능을 확인해보면 train acc는 높고 validation acc는 낮은 경우를 확인할 수 있는데, 이는 과적합 증상의 일부처럼 보이기도 하는데요. 실제로, uni-modal에서 multi-modal로 바뀌면서 파라미터도 두배 이상 많아지고, 이로인해 과적합이 발생하는 것일 수도 있습니다.

이러한 과적합을 해결하기 위해서 2가지 접근법이 있는데요. 첫 번째는 과적합을 줄이기 위해서 drop-out, pre-training, early stopping을 사용하는 것입니다. 두 번째는 과적합이 구조적 결함 때문에 발생하는 것이라 생각하고 이를 해결하는 것인데요. 이를 해결하기 위해서 논문의 저자는 concat, gating(Squeeze-and-Excitation(SE) gate, Non-Local(NL) gate)와 같은 모델을 사용하여 해결해보고자 하였습니다.

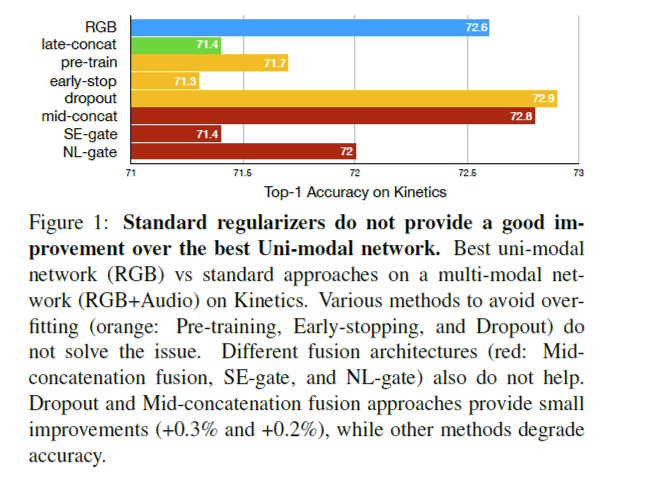
앞에서 말한 방식대로 여러 가지를 실험해봤지만 유의미한 솔루션을 발견하지는 못했는데요. 하지만 Figure 1을 보면, 파라미터가 많은 late-fusion에 비해 파라미터가 적은 dropout, mid-fusion 성능이 높은 것을 통해 overfitting 문제로 인해서 성능이 낮게 나왔음을 확실히 확인할 수 있습니다.

그래서 본 논문은 이러한 overfittng 문제가 발생함을 확실히 알았으니 이를 해결하기 위해서 Gradient-Blending을 제안합니다. 본 논문의 contribution은 아래와 같습니다.

• We empirically demonstrate the significance of overfitting in joint training of multi-modal networks, and we identify two causes for the problem. We show the problem is architecture agnostic: different fusion techniques can also suffer the same overfitting problem.
• We propose a metric to understand the problem quantitatively: the overfitting-to-generalization ratio (OGR), with both theoretical and empirical justification.
• We propose a new training scheme which minimizes OGR via an optimal blend (in a sense we make precise below) of multiple supervision signals. This Gradient- Blending (G-Blend) method gives significant gains in ablations and achieves state-of-the-art (SoTA) accuracy on benchmarks including Kinetics, EPIC-Kitchen, and AudioSet by combining audio and visual signals.

<Method>

<Multi-modal training via Gradient-Blending>

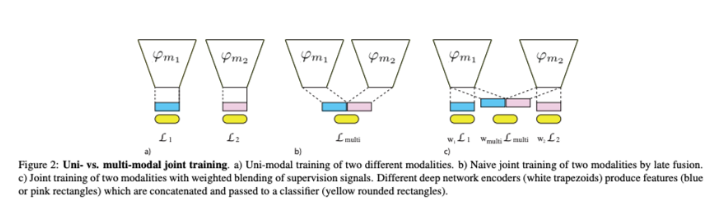
<Background>

<Uni-modal network>

train set $\mathcal{T} = \{X_{1…n},y_{1…n}\}$에서 $X_i$는 i번째 training example이고, $y_i$는 true label인 경우, single modality m (예를 들어서 RGB frame, audio)에 대한 학습은 loss를 최소화하는 것을 의미합니다.

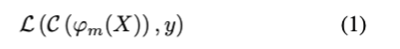
식(1)에서 $ϕ_m$는 일반적으로 파라미터 $Θ_m$을 갖는 deep network이고, C는 일반적으로 파라미터 $Θ_c$를 갖는 하나 이상의 FC layer인 classifier입니다. 이 분류 문제에서 L은 cross entropy loss를 의미합니다. 식(1)을 최소화하면 $Θ^*_m, Θ^*_c$의 해를 구할 수 있는데요. Figure 2a는 두 가지 모달리티 $m_1, m_2$의 독립적인 학습과정을 보여줍니다.

<Multi-modal network>

위의 uni-modal에 이어서 multi-modal network를 학습해봅시다. M개의 서로 다른 모달리티($\{m_i\}^k_1$)에 대해 late-fusion model을 학습합니다. 각 모달리티는 파라미터 $Θ_{mi}$로 구성된 deep network $ϕ_{mi}$로 처리되며, 그 feature가 fusion되어 classifier C로 전달됩니다. Uni-modal network와 마찬가지로 학습은 loss를 최소화하는 방식으로 이뤄집니다.

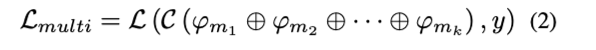
여기서 ⊕는 fusion operation(예를 들어서 concatenation)을 나타냅니다. Figure 2b를 통해 두가지 모달리티 $m_1, m_2$가 공통으로 어떻게 학습되는지 확인할 수 있습니다. 식(2)의 multi-modal networks는 식(1)의 uni-modal의 super-set으로, 임의의 모달 $m_i$에 대한 식(1)의 해에 대해서도 $m_i$ 이외의 모든 모달리티를 소거하는 파라미터 $Θ_c$를 선택하면 식(2)에 대해 똑같이 좋은 해를 구성할 수 있습니다. 하지만 본 논문의 저자는 실제로는 이 해를 찾을 수 없다고 하는데요. 그 이유에 대해서 설명해보고자 합니다.

<Generalizing vs Overfitting>

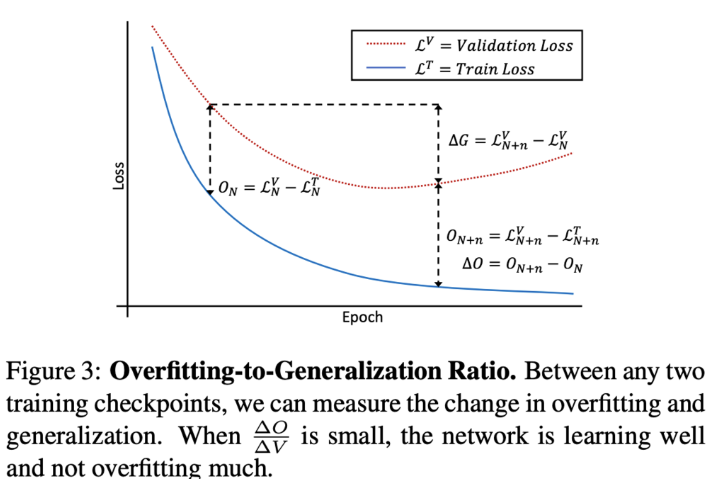
overfitting은 일반적으로 train set에서 target distribution에 일반화되지 않는 패턴을 학습하는 것으로 이해되는데요. epoch N에서 모델 파라미터가 주어졌을 때, $\mathcal{L^T_N}$을 고정된 train set에 대한 모델의 평균 loss, $\mathcal{L^*_N}$을 가상의 target distribution에 대한 실제 loss라고 합시다. epoch N에서의 과적합을 $\mathcal{L^T_N}$과 $\mathcal{L^*_N}$(figure 3에서 $O_N$으로 근사화) 사이의 gap을 정의합니다. 두 모델 체크포인트 사이의 학습의 quality는 overfitting과 generalization의 변화로 측정할 수 있습니다(figure 3의 ∆O, ∆G). 체크포인트 N과 N+n 사이에서 overfitting-to-generalization-ratio (OGR)을 정의할 수 있습니다.

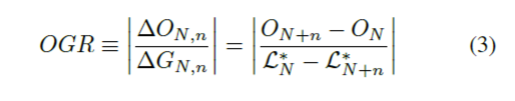
체크포인트 사이의 OGR은 학습된 정보의 quality를 측정합니다. (cross-entropy loss가 있는 경우, 일반화할 수 없는 비트량과 일반화할 수 있는 비트량의 비율입니다.) 학습 중에는 OGR을 최소화하도록 하는데요. 하지만 OGR을 globally하게 최적화하는 것은 매우 비용이 많이 듭니다. (예를 들어서 전체 최적화 tragectory에 대한 변형 방법이 있습니다) 또한, 매우 underfit한 모델도 여전히 높은 점수를 받을 수 있는데요. (underfitting 모델의 경우 train loss와 validation loss의 차이가 매우 작습니다, 즉 O가 작다는 것이죠)

따라서 본 논문의 저자는 gradient에 대한 여러 추정치가 주어지면 이를 blending 즉, 혼합하여 극미소한 $\text{OGR}^2$을 최소화하여 극미소한 문제를 해결하고자 하였습니다. 이 bledning을 최적화 프로세스에 적용하는데요. 최적화 프로세스는 예를 들어서 momentum을 가진 SGD라고 말할 수 있겠네요. 이제 각 gradient 단계는 일련의 valdation loss에 대한 단위 이득 당 일반화 error를 최소화하도록 하작용하여 과적합을 최소화합니다. multi-modal setting에서, 이는 여러 modal의 gradient 추정치를 결합하고 $\text{OGR}^2$을 최소화하여 각 gradient 단게가 single best modality보다 더 나쁘지 않은 이득을 생성하도록 한다는 의미입니다.

gradient에 대한 추정치 $\hat{g}$가 있는 단일 파라미터 업데이트 단계에 대해서 말해보도록 합시다. 두 체크포인트 사이의 거리가 작기 때문에 (gradient step이 학습 loss를 줄이도록 보장이 되는 neighborhood에서) 1차 근사치를 사용하도록 합니다. 1차 근사치는 $∆G ≈ <∇\mathcal{L}^∗, \hat{g}>$과 $∆O ≈ <∇\mathcal{L}^T – \mathcal{L}^*, \hat{g}>$을 의미합니다. 따라서, single vector $\hat{g}$에 대한 $\text{OGR}^2$는 아래와 같습니다.

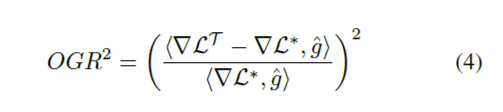
<Blending of Multiple Supervision Signals by OGR Minimization>

Figure 2c를 참고하면, 각 모달리티의 feature와 퓨전된 feature를 classifier에 연결함으로써 여러 가지 gradient 추정치를 얻을 수 있는데요. 각 모달리티별 기울기 $\{\hat{g}_i\}^k_{i=1}$은 각 loss를 개별적으로 back-propagating 하여 얻습니다. (따라서 모달리티별 gradient는 network의 다른 부분에 많은 0을 포함합니다). 다음 결과를 사용하면 더 나은 일반화 동작을 가진 단일 벡터로 blending할 수 있습니다.

<Proposition 1> (Optimal Gradient Blend>

$\{v_k\}^M_0$을 $∇\mathcal{L}^*$에 대한 추정치 집합으로, 과적합이 $\mathbb{E}[<∇\mathcal{L^T}-∇\mathcal{L}^*, v_k><∇\mathcal{L^T}-∇\mathcal{L}^*,v_j>] = 0$을 만족하는 $∇\mathcal{L}^*$의 추정치를 $j=/=k$의 경우라고 합시다. 제약 조건 $\sum_k w_k =1$이 주어지면 문제에 대한 optimal weight $w_k\in\mathbb{R}$은 다음과 같이 주어집니다.

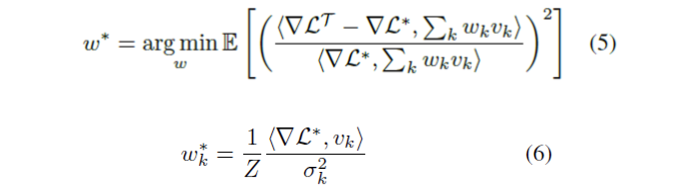
여기서 $\sigma^2_k \equiv \mathbb{E}[<∇\mathcal{L^T}-∇\mathcal{L}^*, u_k>^2]$와 $Z=\sum_k \frac{<∇\mathcal{L}^*,v_k>}{2\sigma^2_k}$는 normalizing constant를 의미합니다.

두 모델의 과적합이 상관관계가 높을 때 가정 $\mathbb{E}[<\triangledown \mathcal{L^T}-\triangledown\mathcal{L}^*,v_k><\triangledown \mathcal{L^T}-\triangledown\mathcal{L}^*,v_j>]=0$는 false가 될 것입니다. 그러나 이 경우, gradient를 blending 해도 얻을 수 있는 것은 거의 없는데요. 본 논문의 저자는 실제로 이러한 cross terms이 $\mathbb{E}[<∇\mathcal{L^T}-∇\mathcal{L}^*, u_k>^2]$에 비해 작은 경우가 많다는 것을 관찰했다고 하는데요. 이는 모달리티 간 상호 보완적인 정보 때문일 가능성이 높으며, 공동 학습이 neuron 간 상호 보완적인 특징을 학습하려고 시도하면서 자연스럽게 발생하는 것으로 추측됩니다.

Proposition 1은 여러 추정치를 blending할 때 잘 알려진 결과와 비교할 수 있는데요. 예를 들어 평균의 경우, 상관관계가 없는 추정치를 개별 분산에 반비례하는 가중치로 혼합하여 최소 분산 추정치를 얻을 수 있습니다.

<Use of OGR and Gradient-Blending in pratice>

자 그럼, multi-task architecture를 적용하여 위의 최적화에 대한 대략적인 솔루션을 구축해보시다.

<Optimal blending by loss re-weighting>

각 backpropagation 단계에서, $m_i$의 모달리티 별 gradient는 $\triangledown\mathcal{L}_i$이고, 퓨전된 loss의 gradient는 식(2)에 의해 주어집니다. 따라서 blended loss의 gradient를 아래와 같이 취하면 blended gradient $\sum^{k+1}_{i=1}w_i\triangledown\mathcal{L}_i$가 생성됩니다.

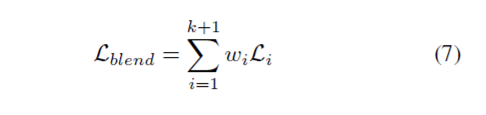
$w_i$를 적절히 선택하면 gradient beldning을 손쉽게 구현할 수 있는데요., 직관적으로 loss weight 재조정은 learning schedule을 재조정하여 다양한 모달리티의 일반화/과적합률의 균형을 맞출 수 있습니다.

<Measuring OGR in pratice>

실제로는 $\triangledown\mathcal{L}^*$를 사용할 수 없는데요. 그래서 본 논문에서는 OGR을 측정하기 위해서, trani set의 subset $\mathcal{V}$을 통해 실제 distribution(즉, $\mathcal{L^V}\approx\mathcal{L}^*$)로 근사화 합니다. loss 측정값을 acc metric으로 대체하여 G와 O를 계산하고, gradient blending에서 optimal weight를 추정합니다. 본 논문에서는 계산 비용을 줄이기 위해서 weight를 너무 많이 변형하기 않고 데이터의 작은 subset에서 weight 추정을 수행할 수 있도록 합니다.

Gradient-Blending 알고리즘은 training data $\mathcal{T}$, validation set $\mathcal{V}$, k input modality $\{m_i\}^k_{i=1}$과 joint head $m_{k+1}$를 입력으로 받습니다. (Figure 2c를 참고해주시면 더 이해가 빠를 것 같습니다). 실제로는 train set $\mathcal{T’}$의 subset을 사용하여 train loss/acc를 측정할 수 있습니다. N개의 epoch에 대해 학습할 때 gradient-blending weight를 계산하기 위해 Algorithm 1에서의 Gradient-Blending weight estimation을 참고합니다.

본 논문에서는 두가지 버전의 gradient blending을 제안하는데요. 이는 아래와 같습니다.

1. Offline Gradient-Blending Offline Gradient-Blending은 gradient-blending의 simple 버전인데요. weight를 한 번만 계산하고 고정된 weight set을 사용하여 전체 epoch를 학습합니다. Algorithm 2를 참고하시면 더욱 이해하기 쉬울 것 같습니다.
   

2. Online Gradient-Blending

Online Gradient-Blending은 full 버전이라고 생각하시면 되겠는데요. 정기적으로 weight를 다시 계산하고(super epoch이라고 하는 n개의 epoch마다), super poech에 대한 새로운 weight로 모델을 학습합니다. Algorithm 3를 참고하시면 더욱 이해하기 쉬울 것 같습니다.

<Experiments>

데이터셋은 세개의 비디오 데이터셋을 사용하는데요, Kinetics, mini-sports, mini-AudioSet입니다. 본 논문에서 사용한 백본은 RGB와 optical flow를 위한 visual backbone으로 ResNet3D를 사용하였구요. 오디오 모델로는 ResNet-50을 사용하였다고 합니다. fusion 모델의 경우, visual 및 audio 백본의 feature에 두개의 FC-layer를 사용하여 concat한 뒤 prediction layer를 통해 예측합니다.

<Overfitting Problems in Navie Joint Training>

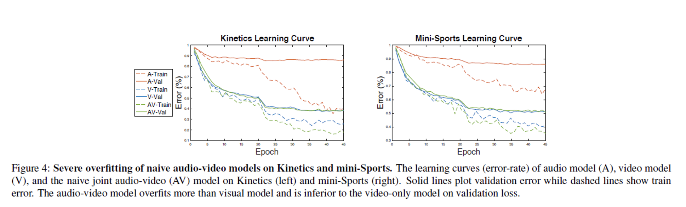
먼저 naive audio-RGB joint training과 unimodal audio-only와 RGB-only training을 비교하였습니다. Figure 4를 통해서 Kinetics(왼쪽), Mini-Sports(오른쪽)에 대한 training curve를 확인할 수 있습니다. 두 데이터셋 모두에서 audio 모델이 가장 많이 과적합 되고 video가 가장 적게 과적합 한다는 것을 확인할 수 있는데요. naive joint audio-RGB 모델은 video-only 모델에 비해 training error는 낮고 validation error는 높습니다. 즉, naive audio-RGB joint training은 과적합을 증가시켜 video-only에 비해 정학도 저하를 가져왔음을 확인할 수 있습니다.

<Gradient-Blending is an effective regularizer>

<Online G-Blend>

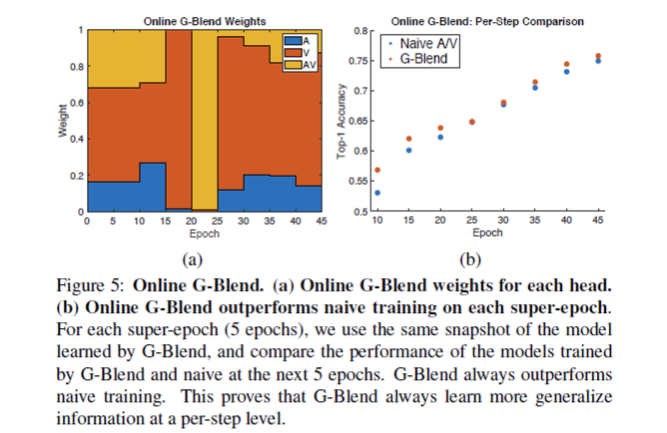
먼저 Online G-Blend에 대해서 살펴볼까요? 초기 super epoch은 워밍업용으로 10으로 설정하고 그 이후에는 5로 가져갑니다. RGB-audio setting의 Kinetics에서 online Gradient-Glending은 uni-modal과 mult-modal baseline을 각각 3.2%, 4.1% 향상시켰습니다. Figure 5a를 통해 online에서의 weight를 확인할 수 있습니다.

게다가, Figure 5b를 통해서 online setting에서 항상 G-Blend가 naive training보다 성능이 우수하다는 것을 확인할 수 있는데요. 동일한 초기화로 super epoch 후 G-Blend 모델과 naive training의 성능을 비교하면 G-Blend 모델이 항상 성능이 naive training보다 높은 것을 확인할 수 있으며 이는 G-Blend가 항상 더 일반화 가능한 training information을 제공한다는 것을 보여주며, propostion 1을 경험적으로 증명함을 보입니다.

<Offline G-Blend>

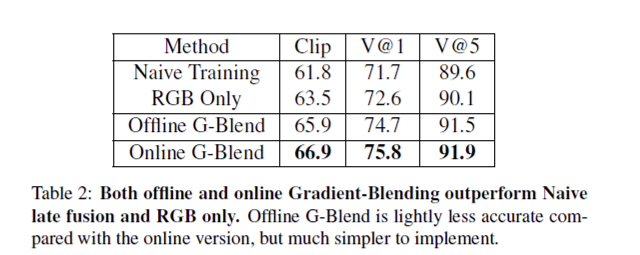
Online G-Blend가 잘 동작한다는 것을 확인했으니, 이제는 Offline G-Blend가 잘 동작하는지 확인해보고자 합니다. online G-Blend를 적용하면 성능 향상을 보이고 오버피팅 문제도 잘 해결하는 것을 보였지만 구현하기가 더 복잡하고 추가 weight 계산으로 인해서 속도가 다소 느리다는 단점이 있습니다. 그에 반해 offline G-Blend는 구현하기 쉽다는 장점이 있죠. 그러면 성능은 과연 어떨까요? Table 2를 봐주세요. Kinetics에서 동일한 Audio-RGB 셋팅에서, offline G-Blend는 unimodal baseline과 naive joint training 보다 각각 2.1%, 3.0%의 큰 차이로 성능이 뛰어남을 보여주며 offline G-Blend도 잘 동작한다는 것을 보여줍니다.

<SOTA>

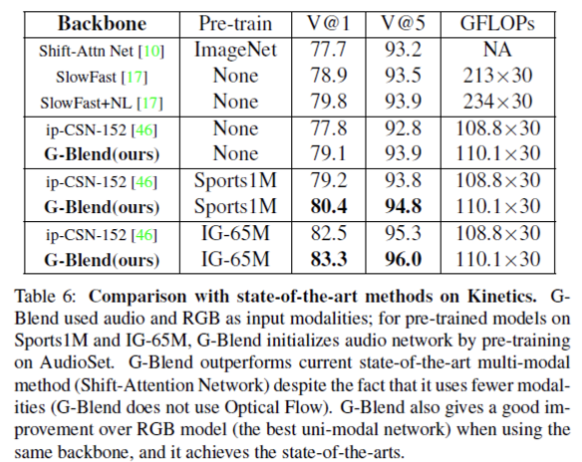
Table 6을 통해 Kinetics에서 SOTA와의 비교를 확인할 수 있는데요. 두 모델을 처음부터 학습시켰을 때 G-Blend는 동일한 백본인 ip-CSN-152를 사용하는 RGB 모델보다 1.3% 향상된 성능을 확인할 수 있습니다.

---

이렇게 리뷰를 끝내보겠습니다. CVPR에다가 제목이 굉장히 흥미로워서 읽게 되었는데요. gradient를 직접 blending하는 방법론이다 보니, 글에 수식이 너무 많이 나와서 읽는데 굉장히 어려웠던 것 같습니다. 제 리뷰가 도움이 되었으면 하는 마음으로 정리해보겠습니다. 읽어주셔서 감사합니다.