안녕하세요! 이번에는 저번에 리뷰했던 GGE의 후속 논문인 GGD를 가져와봤습니다! 지난번과 마찬가지로 de-bias에 초점을 맞춘 논문이고요. 차이점이 있다면 GGE의 경우 VQA task에서의 de-bias를 초점을 맞췄다면 이번 논문은 VQA task 뿐만 아니라 다른 task에서도 적용 가능한 방법론을 다뤘다는 것이 차이점이라 할 수 있습니다. 그럼 시작해보겠습니다!

<Introduction>

논문의 시작은 이렇습니다. 논문의 저자는 딥러닝 대부분의 접근 방식이 데이터 기반으로하며, train data와 test data가 동일한 분포에서 추출되었다는 가정에 크게 의존한다고 말하는데요. 이러한 경우, 보통 out-ot-distribution 이거나 biased setting 때는 일반화하기 어렵습니다. 이러한 한계는 supervised training에서 주어진 sample과 label 간의 상관 관계만 반영하기 때문에 발생하는데요. 이러한 경우 dataset-specific bias를 반영할 수 있고, task의 본질적인 특성을 반영하지 못할 수 있습니다. 일반적으로, supervised objective function fitting paradigm에서, 모델은 bias를 통해서 높은 정확도를 달성할 수 있다면, 모델이 task의 본질적인 요소를 더 배우려는 동기가 감소함을 나타내는데요. 예를 들어서 NLP에 QA task에서 흔히 사용하는 SQuAD 벤치마크가 있습니다. SQuAD에서는 학습된 QA 모델이 질문 단어 주변의 텍스트를 문맥과 상관없이 answer로 선택하는 경항이 있습니다. 또 다른 예로는 제가 이전에 여러번 언급했던 VQA에서 시각 정보를 고려하지 않고 질문과 답변 간의 상관 관계만으로 결과를 도출하는 것이 있겠네요.

모델이 데이터셋에 존재하는 편향으로 인해서 task의 본질적인 특성을 반영하지 못한다는 것을 발견한 연구자들은 데이터셋에 어떠한 bias가 존재하는지 분석하기 시작했는데요. VQA의 language bias, Biased-MNIST의 color bias, image classification의 gender/background bias, ubiquitous long-tailed distribution과 같은 bias를 찾아냈습니다. 이러한 연구 결과를 바탕으로 명시적 de-bias method를 사용하여 성능을 개선하였는데요. 하지만, 이러한 방법은 연구용 데이터셋에서의 bias를 제거하여 성능을 올린 것이지 실제로 real world dataset에 존재하는 bias와 일치하지 않는 특정 bias 하나만 완화 할 수 있다는 단점이 있습니다.

최근의 일부 연구는 implicit method와 같이 명시적인 task 사전 지식 없이 bias를 발견하려는 시도를 계속해서 하고 있는데요. 다만 이러한 방법들은 다소 복잡하고, bias가 잘 알려진 상황일 때 명시적인 방법론 보다 성능이 떨어지는 경우가 많습니다.

그런데, 사실은 dataset bias는 보다 간단한 방법으로 줄일 수 있는데요. Fig 1에서 볼 수 있듯이 bias로 학습된 feature은 데이터셋의 대다수 sample group에만 일반화 할 수 있기 때문에 “suprious”로 간주되니다. 모델이 supurious 상관관계가 성립하지 않는 소수 그룹에서 높은 training error를 발생시킬 수 있지만, 다수 그룹의 우세한 낮은 평균 training error로 인해 전체 loss는 여전히 local minimum에 갇히게 됩니다. core feature(예를 들어서 semantics of objects)에 비해 distractive information(에를 들어서 background)로 인한 bias를 식별하는 것은 상대적으로 쉬운데요. 어떤 instance의 subset이 spurious features와 관련이 없는지 미리 알 수 있다면, 모델이 이러한 sample에 집중하도록 유도하여 예상치 못한 상관관계를 줄일 수 있습니다. 이러한 개념을 도입하여 방법론을 구축한 것이 바로 제가 이전에 리뷰한 GGE 방법론 입니다. GGE는 일련의 bias된 모델을 greed하게 학습한 다음 biased 모델과 기본 모델을 funtional space에서 gradient descent와 같이 ensemble합니다. bias된 모델의 gradient는 자연스럽게 특정 spurious correlation가 있는 sample의 난이도를 나타냅니다.

논문의 contribution을 정리하면 아래와 같습니다.

1. We present a de-bias framework, General Greedy Debias Learning, which encourages unbiased based model learning by the robust ensemble of biased models. GGD is more generally applicable compared to task-related explicit de-bias learning methods while more flexible and effective compared to implicit de-bias methods.
2. We propose Curriculum Regularization for GGD, which results in a new training scheme GGDcr that can better alleviate the “bias over-estimation” phenomenon. Compared with previous methods[36], [37], GGDcr comes to a better trade-off between in-distribution and out-of-distribution performance without either extra unbiased data in training or model ensemble in inference.
3. Experiments on image classification, question answering, and visual question answering demonstrate the effectiveness of GGD on different types of biases.

<Method>

<A. Preliminaries>

먼저 방법론에 들어가기 전에서 이 논문에서 사용하는 notation에 대해서 먼저 설명드리고자 합니다. $(X,Y) \in \mathcal{X} \times \mathcal{Y}$는 training set을 의미합니다. $\mathcal{X}$은 feature space of observation을 의미하고, $\mathcal{Y}$는 label space를 의미합니다. 사전지식을 이용하여 추출할 수 있는 task-specific bias feature의 set은 $\mathcal{B}=\{B_1, B_2, …, B_M\}$로 표현합니다. 예시를 들자면 Biased-MNIST의 texture featuress나 VQA의 language shortcht을 말할 수 있습니다. 이에 따라, $h_m(B_m;φ_m):B_m → \mathcal{Y}$은 특정 biased feateure $B_m$을 이용하여 학습한 biased model이라고 말할 수 있습니다. 여기서 $φ_m$은 $B_m$을 label space $\mathcal{Y}$로 mapping하는 $h_m(.)$의 parameter set이라 말할 수 있습니다. 비슷하게, $f(X;θ):\mathcal{X}→\mathcal{Y}$은 base model을 의미합니다. 예를 들자면 inference 용으로 사용될 target model이라고 말할 수 있겠네요. 지도 학습의 경우, training objective는 예측과 label Y 사이의 거리를 아래 식(1)과 같이 최소화하는 것이며, 여기서 loss 함수는 cross-entropy (CE), bineary cross-entropy (BCE), triplet loss 와 같은 loss를 사용할 수 있습니다. 논문에서는 classfication task가 datasetset bias 문제를 겪는 일반적인 task라는 것을 고려하여 classification task를 예시로 삼았습니다.

<B. Greedy Gradient Ensemble>

식 (1) 상황에서, $f(.)$은 over-parameterized된 DNN으로 선택되었는데, 데이터셋의 bias에 과적합하기 쉽고 일반화 능력이 떨어지는 모델로 만들기 위해서 입니다. 이러한 모델의 과적합이 쉬운 특성을 활용하여 bias model $\sum^M_{m=1} h_m(B_m;φ_m)$와 base model $f(X;θ)$의 ensemble을 label Y에 fit 합니다.

이상적으로는 spurious correlation이 bias model에 의해서만 과도하게 적합되어 상대적으로 bias되지 않은 데이터 분포로 base model f(.)을 학습할 수 있기를 바랍니다. 이를 달성하기 위해서 GGE는 bias된 모델이 데이터 set에서 더 높은 우선순위를 갖도록 유도하는 greedy stratey를 사용합니다.실제로, f(.)는 image classication의 경우 ResNet, VQA의 경우 UpDn 등이 될 수 있으며, h(.)는 texture bias의 경우 low capability model, question shortcut의 경우, question-answer classifier 등이 될 수 있습니다.

funtional space에서 일반적인 ensemble model을 볼 때, $\mathcal{H}_m = \sum^m{m’=1}h_{m’}(B_{m’})$이고, loss $\mathcal{L}(σ(\mathcal{H}_{m+1}h_{m+1}(B_{m+1})),Y)$이 감소하도록 $\mathcal{H}_m$에 $h_{m+1}(B_{m+1})$을 더하고자 한다고 가정해보겠습니다. 이론적으로 원하는 $h_{m+1}$의 방향은 $H_m$에서 L의 negatice derivative여야 합니다. 식으로 표현하면 아래와 같습니다.

여기서 H_{m,j}는 전체 C 클래스 중 j 번째 클래스에 대한 예측을 나타냅니다. classifiacation task의 경우, class j에 대한 확률인 σ(f_j(x))\in(0,1)에만 집중하는데요. 그러므로, negative gradient를 classification을 위한 peuso label이라고 할 수 있고, 새로운 모델 h_{m+1}(B_{m+1})을 아래와 같이 optimize 합니다.

모든 biasd model을 합친뒤에, base model f는 아래와 같이 최적화 됩니다.

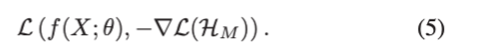
test stage에서는, base model만 prediction에 사용합니다.

위의 패러다임을 mini-Batch Gradient Decent(MBGD)에 적용하기 위해 Algorithm 1과 같이 iterative optimization 방식을 사용합니다. 본 논문의 framework는 biased model과 base model을 동시에 학습시키는데, 이는 bias 모델을 다른 독립적인 프로세스나 추가 annotation을 통해 학습하는 기존 연구와는 다름을 말씀드립니다.

<C. General Greedy De-Bias Learning>

$\text{GGD}_{gs}$(GGE)는 데이터셋의 bias을 과도하게 추정하는 경우가 많은데요. out-ot-distribution data에서는 많은 개선을 이루지만 in-distribution settin에서는 성능이 크게 저하될 수 있습니다. 그래서 본 논문의 저자는 이러한 문제를 극복하기 위해서 CE loss(식(6))에서 GGE의 bias된 모델을 식(7)로 다시 분석합니다.

여기서 $Z=\{z_j\}^C_{j=1}$은 예측된 logitsdlrh, $y_i \in \{0,1\}$은 j번째 class의 ground-truth label을 나타냅니다. $σ_j$은 j번째 class에서 biased model의 confidence를 나타냅니다. loss function의 negative gradient는 식(8)과 같습니다.

pseudo label의 범위를 classification label space [0,1]과 일치하기 위해 $−∇L(z_j)$을 식(9)와 같이 잘라줍니다.

negative gradients는 특정 biased model에서 포착한 spurious correlation를 기반으로 sample을 해결할 수 있는지 여부를 파악합니다.

이제 functional space에서 gradient descent라는 관점을 제처두고, $−∇\hat{\mathcal{L}}$을 pseudo label로 사용하여 CE loss를 decompose할 수 있습니다.

여기서 reference prediction $\hat{σ}=Y\odotσ$이고 $\odot$는 식(9)의 clipping과 동일한 element-wise product입니다.

식(10)을 따르면, gradient ensemble은 ground-truth와 일치하지만 model과 일치하지 않는 prediction을 제공하는 것을 실제로 목표합니다. $-\mathcal{L}_{CE}(f(X), \hat{σ})$는 감소시킬 spurious relation의 정도를 제어합니다. 이를 위해 $\mathcal{L}_{CE}(f(X), \hat{σ})$를 정규화로 취급할 수 있습니다.

여기서 $λ_t$는 regularization term의 weight를 의미합니다. 이보다 일반적인 framework를 General Greedy De-bias (GGD)라고 하며, greedy strategy만 유지하되 negative gradient supervision에서 벗어나는 방식입니다. GGE는 $λ_t=1$일 때 GGD의 special case 입니다. 앞으로는 GGE를 $\text{GGD}_{gs}$라고 표시하도록 하겠습니다.

또한 Curriculum Learning에서 영감을 얻어서, $-\mathcal{L}_{CE}(f(X),\hat{σ})$은 curriculum sample selection function에 대한 “soft” difficulty measurement로 간주할 수 있습니다. 실제로는 training 과정과 함께 $λ_t$를 점진적으로 증가시키는 Curriculum Regularization training scheme ($GGD_{cr}$)을 공식화 합니다. 이러한 방식으로 label과 spurious correlation가 있는 sample도 training의 초기 단계에 참여할 수 있습니다. 이후 학습 단계에서 model은 biased model로는 해결할 수 없는 어려운 sample에 집중하여 out-of-distribution data를 보다 안정적으로 예측할 수 있습니다. 전체 최적화 절차 $GGD_{cr}$은 Algorithm 2에 나와있습니다. 또한 $GGD_{gs}, GGD_{cr}$의 비교는 Fig 2를 통해 확인할 수 있습니다.

<D. Discussions>

1. intuitive Explanation of GGD

좀 더 직관적으로 GGD_gs는 re-sampling strategy으로도 간주할 수 있습니다. biased model로 맞추기 쉬운 sample의 경우, $-∇\hat{L}(z_i)$(즉, base 모델에 의해 생성된 pseudo label)는 상대적으로 작아집니다. 따라서 f()는 이전의 ensemble bias classifier로는 맞추기 어려운 sample에 더 많은 주의를 기울이게 됩니다. 결과적으로 base model은 biased feature를 학습할 가능성이 낮아집니다. 이 과정은 Fig 9를 통해서 구체적으로 확인할 수 있습니다.

하지만, 식(9)에 따르면, 높은 spurious correlation을 보이는(즉, $-∇\hat{L}(z_i)=0)$ sample은 버려지게 됩니다. 만약 zero supervision으로 인해 large groups of data가 없는 경우, gradient supervision을 사용하는 base 모델의 representation learning이 과소 적합될 수 있습니다. 또한, label distribution이 VQA-CP distribution bias처럼 왜곡된 경우, base 모델은 label의 bias을 과도하게 추정할 수 있게됩니다. 이로 인해 “inverse” training bias가 발생하고, indistribution test data에서 크게 성능이 저하됩니다. long-tailed classification에서도 비슷한 결과가 나타났는데, 데이터 일부를 다시 샘플링하면 더 균형 잡힌 classifier가 만들어지지만 representation learning에 안좋은 영향을 미치는 반면, unbalaced data로 학습하면 classifier가 bias되지만 여전히 좋은 representation을 제공한다는 것을 보여줍니다.

“bias over-estimation”을 완화하기 위해 GGD_cr은 gradient supervision을 ‘softer’ Curriculum Regularization로 대체하여 GGD_gs를 완화시킵니다. $λ_t$를 조정하면 모든 데이터가 초기 단계에서 base 모델 학습에 참여할 수 있으므로 bias over-estimation을 잘 완화할 수 있습니다.

2. Probabilistic Justification

sample x가 주어진다고 해봅시다. $x^b$는 biased feature이고, $x^{-b}$는 bias를 제외한 feature라고 합니다. label y가 주어졌을 때, $x^b, x^{-b}$는 조건부 독립적입니다. 이를 식으로 표현할 수 있는데요.

여기서 C는 주어진 데이터셋과 관련된 constant term 입니다. 자세한 도출 방법은 부록에 나와있다고하니 참고하실 분은 참고하면 좋을 것 같네요. task의 core feature($x^{-b}$)를 구별하는 것은 어렵지만, 사전 지식을 바탕으로 dominant biases($x^b$)를 식별하는 것은 더 쉽습니다. 식(12)는 likelihood log $p(y|x^{-b})$를 최대화 하는 것은 $log p(y|x)$를 최대화하면서 $log p(y|x^b)$를 최소화하는 것과 같다는 것을 나타냅니다.

최적의 biased model $h(x^b;φ^*)$이 아래 식(13)을 가진다고 가정해봅시다.

$q_{φ^*}(y|x^b)$를 최적의 biased prediction $h(x^b,φ^*)$의 분포로 간주합니다. GGD는 p(x|y)와 biased reference $q_{φ^*}(y|x^b)$ 사이의 차이를 확대하여 log $p(y|x^b)$를 최소화합니다. 식(12)를 최대화하면 다음과 같이 근사화됩니다.

여기서 θ는 distribution p(y|x)를 생성하는 base model의 매개변수이고, D(.||.)는 두 분포 사이의 차이를 의미합니다. 실제로는 p(y|x)와 q(y|x^b) 사이의 CE를 최대화하여 다양한 예측을 얻습니다. 식(12)는 probabilistic formulation에서 GGD의 새로운 정당성을 제공하는데, 이는 log p(y|x^{-b})의 log-likelihood를 최대화 하는 것을 목표로 합니다. 또한, q(y|x^b)의 정밀도가 매우 중요한데요. biased 모델이 실제 correspondence를 너무 많이 포착하는 경우, divergence를 최대화하면 base 모델에 해를 끼칠 수 있습니다.

3. On the Trade-off between ID and OOD performance

greedy ensemble의 핵심 아이디어는 boosting strategy와 비슷한데요. 부스팅은 bias는 높지만 분산이 낮은 여러 개의 약한 classifier를 결합하여 bias가 낮고 분산이 낮은 강력한 classifier를 생성하는 것입니다. 각 base learner는 충준히 약해야하며, 그렇지 않으면 처음 몇 개의 classifier가 학습 데이터에 쉽게 과적합됩니다. weak learner를 모두 조합하는 부스팅과는 달리, 이 과적합 현상을 활용하되 예측에는 마지막 base model만 사용합니다. 이 전략은 biased된 모델과의 특정 허위 상관관계를 제거하지만 단일 base 모델에 대한 bias-overestimation도 발생합니다. 이 문제를 해결하기 위해 GGD는 초기 학습 단계에서 모든 ID 데이터로 모델을 학습한 다음 점차적으로 hard sample에 집중하는 curriculum regularization을 도입했습니다.

ID와 OOD 성능 사이의 trade-off는 이미 OOD 일반화 연구에서 많은 관심을 끌었습니다. 이러한 방법의 대부분은 학습 중에 OOD 데이터를 사용할 수 있다고 가정하거나, bias가 거의 없는 균형 잡힌 데이터 모델을 사전 학습할 수 있다고 가정합니다. 따라서 주어진 OOD 데이터로 모델을 적응적으로 조절할 수 있습니다. 그러나 bias 제거 학습의 경우, OOD 데이터가 없으면 bias 추정이 더 어렵고 까다로워집니다. GGD는 algorithm 2에서와 같이 통합된 프레임워크에서 두 모델을 학습합니다. 원래 모델에 대한 추가 학습 비용이 필요하지 않으며, 어떤 기본 모델에도 잘 적용할 수 있어 실제 애플리케이션에서 더 만은 유연성을 확보할 수 있습니다.

<E. General Applicability of GGD>

이 파트에서는 특정 task에 대한 GGd의 자세한 구현 방법을 설명하고자 합니다. 여기서 h(.)는 biased된 모델을 의미하고, $\hat{y}\in\mathcal{Y}$은 biased된 예측을 나타냅니다.

1. GGD with Single Explicit Bias

한 가지 유형의 bias에 초점을 맞춘 기존의 명시적 bias 제거 방법과 비교하기 위해 먼저 Biased-MNIST의 texture bias에 대해 GGD를 테스트 합니다.

데이터셋 $\mathcal{D}=\{x_i, y_i, b_i\}^N_{i=1}$는 합성 이미지 x_i, annotated된 digit label y_i, 그리고 background color b_i로 구성되어 있습니다. 여기서 입력이미지 x_i로 digit number $\hat{y}_i$를 예측하는 것을 목표로 합니다.

여기서 base model f(.)는 CE loss로 학습된 neural network입니다.

Biased-MNIST의 bias는 digits와 background color 간의 spurious correlation에서 비롯됩니다. 실제로는 두 가지 종류의 bias 모델을 정의 합니다. 첫 번째 경우, 이미지 sample x_i는 biased prediction $B^i_t$는 low capacity model로 추출됩니다.

$h_{1 k}(.)$는 Kernal size 1X1로 구성된 SimpleNet-1k입니다. 작은 receptive field로 인해 local texture cues를 통해서만 이미지의 target class를 예측하게 됩니다.

두 번째 경우에는, bias 추출을 위한 명시적 background b_i를 제공합니다.

$h_{bg}(.)$는 base model과 유사한 일반적인 신경망이지만 입력은 숫자가 없는 배경 이미지 뿐입니다. 따라서 biased model은 순전히 texture bias에 따라 prediction을 수행합니다.

2. GGD with Self-Ensemble

Adversarial QA와 같은 task의 경우, task-specific bias를 구분하기 어렵습니다. 사전 지식이 부족한 상황에서 bias 제거 학습을 위해, 자체 앙상블을 사용하는 보다 유연한 버전의 GGD를 설계하였는데 이를 $GGD^{se}$라고 합니다.

biased prediction $B_{se}$는 아래 식(18)와 같이 포착할 수 있습니다.

여기서 $h_{se}(.)$는 base model과 동일한 architecture 및 opimization scheme을 가진 또다른 신경망 입니다. base model은 일반적으로 dataset bias에 과도하게 맞추는 경향이 있으므로 $h_{se}(.)$는 task-specific prior knowledge가 없어도 bias를 암시적으로 포착할 수 있습니다.

<Experiments>

A. Image Classification

Image Classification Task에서 GGD를 적용했을 때의 성능은 Table 1을 통해서 확인할 수 있습니다. Baseline을 보시게 되면 77.8% 성능을 달성한 것을 볼 수 있는데 GGD라는 debias 방법론을 적용하니 성능이 무려 92%까지 올라간 것을 확인할 수 있습니다.

Fig 3은 Biased MNIST에서 각 class 마다의 ACC를 확인한 것인데 Baseline의 경우 Bias에서 색깔이 더 진한 것을 확인할 수 있는데 GGD의 경우, GT에서 더 색깔이 진한 것을 확인할 수 있습니다. 제대로 de-bias를 했다는 의미로 볼 수 있겠죠? 실험결과가 이렇게 뚜렷하게 나오니 대단한 방법론이라 생각됩니다.

B. Adversarial Question Answering

이제까지 SQuAD 데이터셋이 어떻게 생겼는지 궁금하실 것 같아 예시를 가져와봤습니다. 데이터셋은 Fig 4와 같이 구성되어 있습니다.

이번에는 Baseline 위주로 모델 성능을 비교했는데요. GGD의 경우 model-agnostic 하기 때문에 이렇게 비교하는 것이 가능한 것 같습니다. Table 3을 보게 되면 성능을 확인할 수 있는데요. 이미지 분류에서만큼 큰 폭으로 성능 향상을 한 것은 아니지만 2% 이상의 성능 향상을 이룬 것을 볼 수 있습니다.

C. Visual Question Answering

굉장히 많은 방법론과 비교 성능을 확인할 수 있는 VQA 입니다. 정말 많은 모델과 비교한 것이 대단하다고 느껴지는데요. 역시나 GGD가 baseline에 비해서 성능 향상을 많이 이룬 것을 확인할 수 있습니다. 무려 20% 정도나 향상시켰으니 감탄이 저절로 나옵니다.

Fig 6을 통해서 정성적 평가를 확인할 수 있습니다. 기존의 UpDn 모델의 경우 이미지의 주요 부분을 포착하지 못하는 모습을 보이는 반면에 GGD의 경우에는 제대로 이미지의 주요 부분을 포착함으로써 정확한 대답을 도출하고 있습니다.

---

이렇게 리뷰를 끝내봅니다. 하나의 방법론을 가지고 여러 task에 비교 및 실험을 수행한 것이 정말 대단하다고 느껴진 논문이었습니다. 그리고 실험 task에서 모두 성능 향상을 가져왔다니 대단하다고 말할 수 밖에 없을 듯 합니다. 이런 논문을 쓰고 싶다는 마음이 들게 하는 논문이었던 것 같습니다. 읽어주셔서 감사합니다.