안녕하세요.
오늘 작성할 리뷰는 Test-Time Adaptation, 줄여서 TTA 분야의 논문입니다.

본 논문은 TTA 분야에서 baseline 격이라고도 불리는 논문입니다.
그럼 리뷰 시작하도록 하겠습니다.

1. Introduction

저희가 이때까지 다뤄왔던 여러 딥러닝 모델들은 학습 데이터와 평가 데이터가 유사한 분포를 가질 때 높은 성능을 보입니다. 하지만 이러한 모델들은 새로운 분포의 data에 대해 매우 낮은 일반화 성능을 보이게 되고, 이를 dataset shift, domain shift 에 의한 성능 저하라고 표현합니다. 갑작스런 날씨의 변화, corruption, 자연 변화, sensor degration 등이 이에 해당할 수 있죠.
그럼에도 불구하고 학습 데이터와는 다른 분포를 가질 수 있는, different data distribution으로 모델을 deploy 하는 작업은 필수적이기 때문에, 이러한 상황에서의 adaptation 연구 또한 필요합니다.

Test-Time Adaptation, 줄여서 TTA 는 이름에서도 알 수 있다시피 학습 단계가 아닌 평가 단계에서 adaptation을 수행하는 기법입니다. TTA는 UDA(Unsupervised Domain Adaptation) 와는 달리 adaptation을 수행하는 과정에서 source dataset으로의 접근이 필요하지 않기 때문에 훨씬 더 효율적이고, 실제 real world에서의 무인 이동체 device에 상대적으로 적합한 기술이죠.

Real World에서의 적용을 위한 TTA의 컨셉에 맞게, 본 논문에서도 3가지 포인트에 대해 집중합니다.

1. Availability: 비용적인 이유, 그리고 license 등의 이슈로 인해 source dataset 없이 모델이 배포되는 환경에서도 효율적인 adaptation을 수행해야 한다.
2. Efficiency: Test 과정에서 source dataset에 대한 연산과정(forward, backward)을 수행하는 것이 비효율적일 수 있다.
3. Accuracy: 모델이 특정 목적(test 시 마주하는 상황) 에 adaptation 되지 않으면 정확도가 매우 낮아질 수 있다.

위의 말을 정리하자면,
결국 저자들은 Source Dataset에 대한 접근 없이 오로지 Test-time에서 마주하는 test dataset만을 사용해서 여러 test domain에 대해 adaptatation을 수행하는 Fully Test-Time Adaptation 기법을 설계하였습니다.

본 논문에서는 test 단계에 adaptation을 하는 과정에서, model의 entropy를 최소화 하도록 모델을 update 하게 됩니다. 이 때문에 본 논문에서 제안하는 기법의 이름이 TENT 인 것이구요. 저자들은 test dataset에 대한 supervision을 줄 수 없는 상황에서 model을 잘 adapation 하기 위해 Test 단계에서 모델 예측의 entropy를 최소화 하도록 하였는데, Entropy라는 개념은 크게 2가지 요소와 관련이 있습니다.

1. Entropy는 error와 관련이 있습니다. 모델이 성공적인 예측을 수행한다는 뜻은 예측에 대한 확신(confidence)이 높다는 말이고 이는 entropy, 즉 불확실성이 그만큼 낮다는 것을 의미합니다. 아래 Figure1의 간단한 실험 결과를 보면 알 수 있다시피 entropy와 error가 서로 비례하는 관계임을 알 수 있습니다.
2. Entropy는 curruption과 관련이 있습니다. corruption은 직역하면 ‘부패’ 라는 뜻을 가진 단어인데, DA적 관점에서의 corruption은 기존 domain과 비교했을 때 shift된 정도라고 생각하시면 됩니다. 아래 Figure2가 의미하는 바는, 기존 original domain 대비 여러 domain corruption을 다양한 level로 부여했을 때 entropy와 loss가 비례함을 보여주고 있습니다.

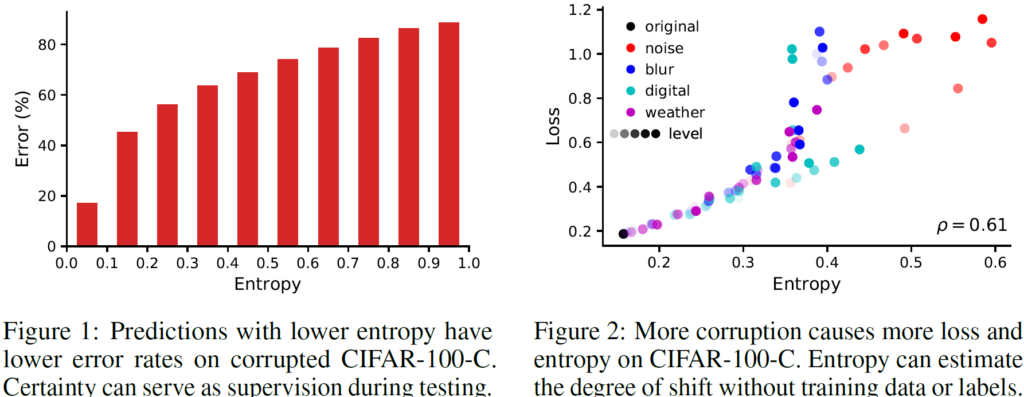
저자는 위 실험을 통해 model 예측의 entropy가 error 그리고 loss와 비례하는 관계임을 보였고, TTA의 특성 상 target domain에 직접적인 supervision을 부여할 수 없는 상황에서 adaptation을 수행하기 위해 entropy를 minimization 하는 기법을 설계하게 됩니다.

과연 Test-Time때 어떻게 entropy를 minimization 하는지, 이 과정에서 모델의 어떠한 parameter가 update 되는지에 대한 자세한 사항들은 아래에서 설명드리도록 하겠습니다.

---

2. Setting: Fully Test-Time Adaptation

Adaptation은 source에서 target domain으로의 generalization을 수행하고자 하는 task 입니다. 이러한 adaptation을 수행하고자 하는 여러 방식들이 있는데, 아래의 표에서 이들과 Fully Test-Time Adaptation 방식의 차별점에 대해 알 수 있습니다.

• x^s: source data
• y^s: source label
• x^t: target data
• y^t: target label
• L(.): loss function

<fine-tuning>
위 4가지 방식 중 저희에게 가장 익숙한 fine-tuning 입니다. 해당 방식은 이미 source data에 대해 학습된 모델을 target data로 supervised loss를 통해 학습하는 방식입니다. 따라서 adaptation이 수행될 때 x^t와 y^t 가 모두 필요합니다. y^t가 필요하다는 점이 큰 제약사항이겠네요.

<domain adaptation>
DA 방식에서는 우선 source domain에 대해 모델을 학습시킨 후 target domain으로 adaptation을 수행하게 됩니다. adaptation이 수행될 때 x^t 뿐만 아니라, source domain의 x^s와 y^s 가 모두 사용된다는 점이 제약사항이 되겠네요. 실제 상황에서는 license, 비용 등의 이유로 source domain에 접근하기 어려운 경우가 많기 때문이죠.

<test-time training>
위 2가지 방식과 달리 test-time traning 방식은 test 단계에서 마주할 수 있는 갑작스런 domain 변화에 대한 adaptation을 고려한 방식입니다. test 단계에서 입력으로 들어오는 x^t에 대해 적절하게 잘 L(x^t)를 설계함으로써 말이죠. 다만 본 논문에서 제안하는 Fully test-time adaptation과는 달리 여전히 source data에 대한 접근이 필요하다는 제약 사항이 존재합니다.

<fully test-time adaptation>
본 논문에서 제안하는 방식입니다. source domain에 대해 학습할 때 사용되는 x^s와 y^s 는 adaptation 단계에서 전혀 사용되지 않습니다. source domain에 대해 직접적인 접근이 어려울 때에도 사용할 수 있을 뿐더러, test 단계에서 source data에 대한 그 어떠한 연산(forward, backward)이 수행되지 않기 때문에 훨씬 더 가볍습니다. 그렇기 때문에 실제 edge device에 적용하는 관점에서도 훨씬 강력하죠.

---

3. Method

introduction 부분에서 설명드렸다시피 본 논문에서는 test 단계에서 모델 예측의 shannon entropy를 최소화함으로써 모델을 최적화해나가며, 해당 기법을 TENT 라고 이름짓습니다.
어떤 목적함수를 최적화 해나가는지에 대한 설명을 3.1절, 그리고 최적화 과정 중 모델의 어떠한 parameter를 update해 나가는지에 대한 설명을 3.2절에서 진행하도록 하겠습니다.

3.1. Entropy Objective

test 단계에서 입력으로 들어가는 영상 x^t에 대한 모델의 예측을 \hat{y}라고 하며, 본 논문에서는 \hat{y}의 entropy인 H(\hat{y})를 최소화 하고자 합니다. 식은 아래와 같습니다.

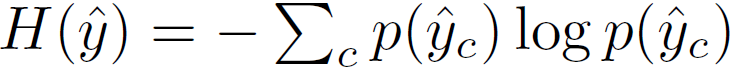
Entropy는 데이터의 label y의 존재 유무와는 관계없이 오로지 모델의 예측에만 의존하기 때문에 unsupervised 목적함수 입니다. 그렇기 때문에 실제 test-time에서 실시간으로 들어오는 입력에 대한 최적화가 가능하죠.

introduction 에서 entropy는 모델의 error, 그리고 loss와 비례하는 관계를 가진다고 설명했기 때문에, 저자는 target data에 대한 직접적인 supervision을 줄 수 없는 상황에서 위의 entropy를 최소화해나갑니다.

3.2. Modulation Parameters

Entropy를 최소화해나간다는 것은 알겠는데, 그러면 모델의 어떤 parameter를 update 한다는 것일까요?
우선 모델의 일반적인 parameter \theta는 source data에 대해 미리 supervised 된 상태로, source data에 대해서만 잘 최적화 되어있는 상태입니다. parameter \theta 라 함은, CNN의 weight, bias로 생각하시면 됩니다.
본 논문에서는 어쨋든 Test-Time때 모델을 update해 나가야 하는데, 그런 관점에서 parameter \theta를 update해 나가는 건 위험하다고 판단하였습니다. 왜냐하면 Fully Test-Time Adaptation 세팅에서는 adaptation 수행 시 source data로의 접근이 불가능한데, 잘 학습된 parameter \theta를 update한다는 것은 기존에 잘 학습된 source representation을 해칠 위험이 있기 때문입니다. 또한 deep learning 모델은 매우 deep 하기 때문에 이러한 상황에서 중간 layer에서 생기는 조금의 변화가 최종 prediction 단계에서는 치명적인 영향을 끼칠 수도 있기 때문입니다.

그래서 저자는 효율적이고 안정적인 최적화를 위해  affine(multiplication, translation)하며 차원 수가 낮은(channel-wise) parameter인 \gamma, \beta 를 선택합니다.

Batch Normalization은 크게 Normalization, Transformation 2가지 단계로 구성되고,
이에 적용되는 parameter로는 총 4개가 존재합니다. 아래 그림 좌측의 \mu, \sigma, \gamma, \beta 가 각각 이에 해당하죠.

<1. Normalization>
입력으로 들어오는 batch의 분포를 평균 0, 분산 1로 만들어 주는 단계입니다. 학습단계 기준으로 \mu는 해당 batch의 평균을, \sigma는 표준편차를 의미합니다. 그리고 평가단계에서는 각 batch별로 계산된 여러 \mu와 \sigma를 각각 평균내어서 사용하게 됩니다.
그런데, TTA에서는 동작 방식이 조금 다릅니다. 방금 위에서 설명드린 방식은 source data와 target data의 분포가 유사하다는 전제가 있기 때문에, 학습때 계산된 여러 \mu와 \sigma를 평균내어서 평가 단계에서 사용하는 것이 가능했던것입니다.
하지만 본 논문에서 풀고자 하는 Test-Time Adaptation은 세팅상 평가 단계에서 source domain과는 매우 상이한 분포의 data가 들어오기 때문에 학습 단계에서 구해진 \mu와 \sigma를 사용하는 것은 위험할 수 있습니다. 따라서 본 논문에서는 TTA 수행 시 입력으로 들어오는 test batch에 대해 \mu와 \sigma를 계산한다고 합니다. 그리고 아래 식을 통해 Normalization을 진행하게 됩니다.

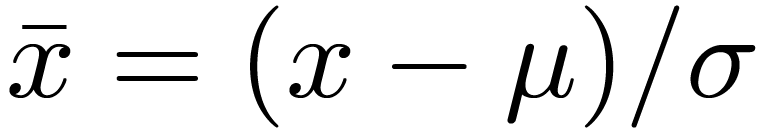
<2. Transformation>
위 Normalization 과정을 통해 입력 batch를 평균 0, 분산 1의 분포로 만들어 주었다면, 이제는 batch norm의 learnable parameter인 \gamma, \beta를 통해 Transformation을 수행하는 단계입니다. 새로운 분포로 \gamma 만큼 scaling 되고, \beta 만큼 shift 한다고 생각하시면 됩니다.

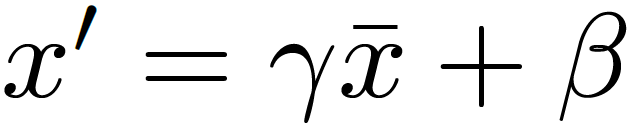
3.3. Algorithm

<Initialization>
우선 source domain에 대해 supervised 방식으로 미리 학습된 모델이 존재합니다.
그리고 학습된 batch norm parameter인 \gamma, \beta는 잘 보존해 두고, 해당 batch norm parameter를 제외한 나머지 parameter \theta는 고정시키게 됩니다.
그리고 위에서 설명드렸다시피 TTA의 특수성 때문에 일반적인 Batch Norm과는 달리 학습때 계산된 여러 \mu와 \sigma 값은 보존하지 않고 버립니다.

<Iteration>
이제 test time의 forward 단계에서 입력으로 들어오는 batch에 대해서 평균과 분산, 즉 Normalization parameter인 \mu와 \sigma를 구하게 됩니다.
또한 backward 단계에서는 위의 3.1절에서 설명드린 Entropy를 계산해서 최적화가 수행되게 됩니다. 이때 나머지 parameter \theta는 모두 고정하고, train data에 대해 미리 계산된 Transformation parameter인 \gamma, \beta 의 update가 수행되게 됩니다.

---

4. Experiment

TTA를 벤치마킹 하기 위한 dataset에 대한 설명은 해당 리뷰 에 자세히 설명해 두었으니 참고하시면 좋을 거 같습니다.

본 논문에서는 classification task 에 대해서 TTA를 수행하게 되는데,
source dataset으로는 일반적인 dataset인 CIFAR-10/100과 ImageNet을 사용하고,
target dataset으로는 앞선 source dataset에 corruption이 적용된 CIFAR-10/100-C과 ImageNet-C을 사용합니다.

설명에 앞서 본 논문의 실험 table에 대한 설명이 조금은 불친절(?)하기 때문에 제 설명 또한 조금 빈약할 수 있음을 양해 부탁드립니다..
아래 실험 table에서 소개 될 benchmark 비교 대상군은 아래와 같습니다.

<source>
아무런 adaptation과정 없이, source에 대해 학습된 classifier를 target에 적용

<RG> – adversarial domain adaptation
2015년에 제안된 방식으로, domain-invariant representation을 학습하기 위해 source와 target을 구별해 주는 domain classifier의 gradient를 reverse 시킨다고 합니다.

<UDA-SS> – self-supervised domain adaptation
source와 target의 shared representation을 모델링하기 위해 rotation과 position을 수행하는 방식으로 self-supervised학습을 진행하는 방식입니다.

<TTT> – test time training
(2절 참조)

<BN> – test time normalization
test 단계에서 target data에 대해 batch nrom statistics를 update 하는 방식이라고 합니다.

<PL> – pseudo labeling
confidence threshold를 조정하면서 pseudo label을 지정하면서 최적화를 진행하는 방식입니다.

위의 방식들 중 BN, PL, 그리고 본 논문의 TENT만 adaptation 수행 시 source data로의 접근이 필요없는, Fully Test-Time Adaptation 입니다.

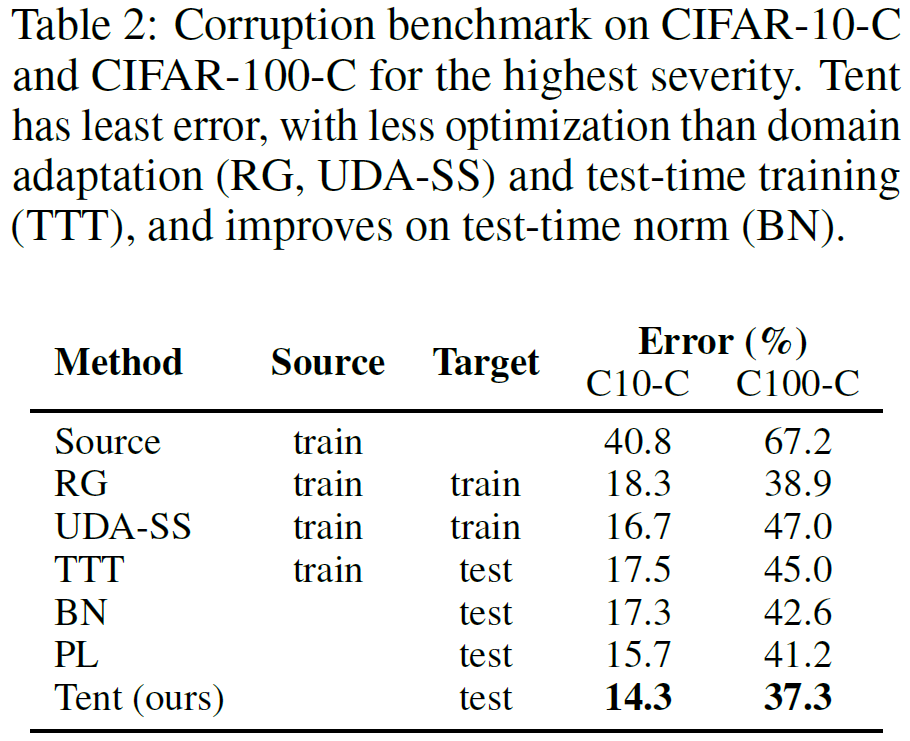
위 실험 결과에서 BN과 Tent의 차이를 통해 Entropy minimization 방식의 효과를 알 수 있습니다. 왜냐면 두 방식 모두 Batch norm param을 update한다는 것은 같은데, 목적함수만 다르기 때문이죠. classification error 기준으로 꽤나 많은 성능 향상을 이뤄내고 있습니다.

또한 adaptation 시 source 로 의 접근이 가능한 UDA-SS, TTT와 비교해서도 높은 성능을 보이고 있다는 점이 의아하면서도 놀랍네요.!

---

오늘 리뷰한 논문은 TTA 분야에서 baseline 격으로 불리는 논문이고, 제시하는 Entropy minimization 방식은 최근 TTA 논문들에서도 계속해서 사용되는 방법론으로 알고 있습니다. 그럼 다음에도 또 다른 TTA 논문으로 찾아 오도록 하겠습니다. 감사합니다.