[3DV 2022]SC6D: Symmetry-agnostic and Correspondence-free 6D Object Pose Estimation

Abstract

해당 논문은 단일 RGB로부터 symmetry-agnostic(객체의 대칭 여부에 관한 정보를 주지 않아도 된다는 의미) 하고 correspoondence-free(3D model을 쓰지 않는 방식이라 이렇게 표현한 것으로 보입니다)의 객체의 6D Pose를 추정하는 프레임워크를 제안합니다. 해당 방법론은 3가지 하위 task로 이루어집니다.

(a) 객체의 3D rotation 표현 학습 및 매칭

(b) 물체의 2D 중심 위치 추정

(c) scale에 무관한 거리 추정

SC6D는 T-LESS, YCB-V, ITODD 데이터에 대해 평가를 수행하였으며 기존 SOTA방법론인 SurfEmb 보다 계산상 효율적이라 합니다.

Introduction

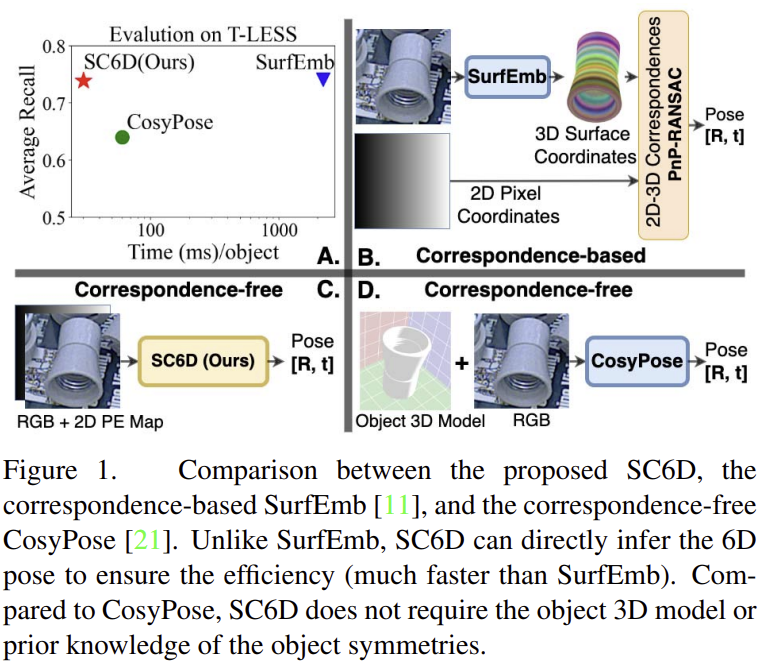
최근 학습 기반의 방식은 대부분 2D-3D 관계를 이용하여 pose를 추정하므로써 정확도 높은 pose를 추정하지만, 이러한 방식은 대칭, texture 누락, occlusion 과 같은 ambiguity로 인해 객체가 시각적으로 모호할 경우 성능 저하가 크게 발생한다는 문제가 있습니다. 1대 1 대응 관계를 이용하는 대신 SurfEmb(Figure1의 B)는 시각적 모호성을 줄이기 위해 one-to-many 2D-3D 대응 분포를 이용하는 방식을 제안하였습니다. SurfEmb는 texture 정보가 거의 없고 대칭적인 산업용 물체로 이루어진 T-LESS 데이터 셋에서 SOTA를 달성하였습니다. 그러나 SurfEmb는 PnP-RANSAC 과정에서 시간이 많이 소요됩니다.

또 다른 기존 연구인 CosyPose(Figure1의 D)는 명시적인 대응 관계를 이용하지 않고 직접적으로 pose를 추론합니다. CosyPose는 계산량을 크게 감소시켰으나, 3D CAD 모델과 대칭 여부와 같은 ambiguity에 대한 사전 지식이 필요하다는 한계가 있습니다. 또한, 추론 과정에도 렌더링을 통해 합성 데이터를 생성하고 refinement를 수행하기 위해 CAD 모델이 필요합니다. 이러한 이유로 실제 활용에 많은 제약이 있습니다.

ambiguity에 무관한 6D Pose Estimator를 학습하 위해 중요한 문제는 대칭 객체가 여러 view에서 동일한 형태를 가지며, 더이상 1대1 대응이 아니라는 것으로부터 시작합니다. 최근의 또 다른 연구인 ImplicitPDF는 ambiguity에 대한 사전 정보 없이 RGB 이미지에서 객체의 3D 회전 분포를 추정할 수 있는 방식이지반, 수백만개의 회전 샘플을 각 객체의 표현 벡터에 연결해야 하므로 계산 효율이 크게 떨어집니다.

본 논문은 대칭 여부와 무관하게 SO(3) 임베딩을 이용하는 correspondence-free 방식인 SC6D라는 방법론을 제안합니다. Implicit-PDF와 달리 SC6D는 SO(3) 공간의 3D 회전 샘플에 대한 representation을 학습하고 cosine similarity를 기반으로 representation과 rotation을 연결합니다. 또한, SC6D는 3D translation을 동시에 추정할 수 있습니다. 추론속도를 높이기 위해 SC6D는 offline 방식으로 각 객체에 대한 3D rotation representation library를 구성합니다. 한편, 3D translation은 regression 방식으로 객체 경계 상자의 중심으로의 offset을 구하고, z축을 따라 객체의 translation을 사전에 정의된 library로 분류하여 구합니다. SC6D는 T-LESS, YCB-V, ITODD 데이터에 대해 SOTA 방식과 비교하고, 어려운 데이터인 T-LESS에서 SOTA 성능(평균 recall 78.0%)를 달성하며 YCB-V와 ITODD 데이터에서 베이스라인과 비슷한 성능을 달성합니다.

Method

RGB 이미지X로부터 6d Pose \mathbf{P} = [\mathbf{R|t}]를 추정하기 위해 객체 중심의 Rotation \mathbf{R}이 아닌, 외부 중심의 방향 \mathbf{R}_{allo}∈R^{3⨉3}을 예측함으로써, 유사한 외부 중심의 방향은 유사한 형태를 가지기 때문에 객체의 표현을 학습하는 데 중요한 역할을 한다고 합니다. YOLO와 Faster-RCNN과 같은 기존 detector의 예측 값을 이용하여 객체 영역에 대한 crop된 rgb 이미지 영역 \mathbf{B}을 이용하여 rotation을 예측하고, 물체 중심의 rotation은 \mathbf{R} = \mathbf{R}_c\mathbf{R}_{allo} (\mathbf{R}_c는 물체의 중심을 통과하는 ray와 카메라의 광축 사이의 3D rotation)를 통해 구하게 됩니다.

SC6D는 3D 모델을 이용하지 않고 crop된 RGB 이미지에서 객체의 3D 방향 분포와 객체의 3D 위치를 추정합니다. 이는 1) RGB 인코더 2) pose 디코더 3) SO(3) 인코더 3가지로 구성되며, 전체적인 아키텍처는 위의 Figure 3을 통해 확인할 수 있습니다.

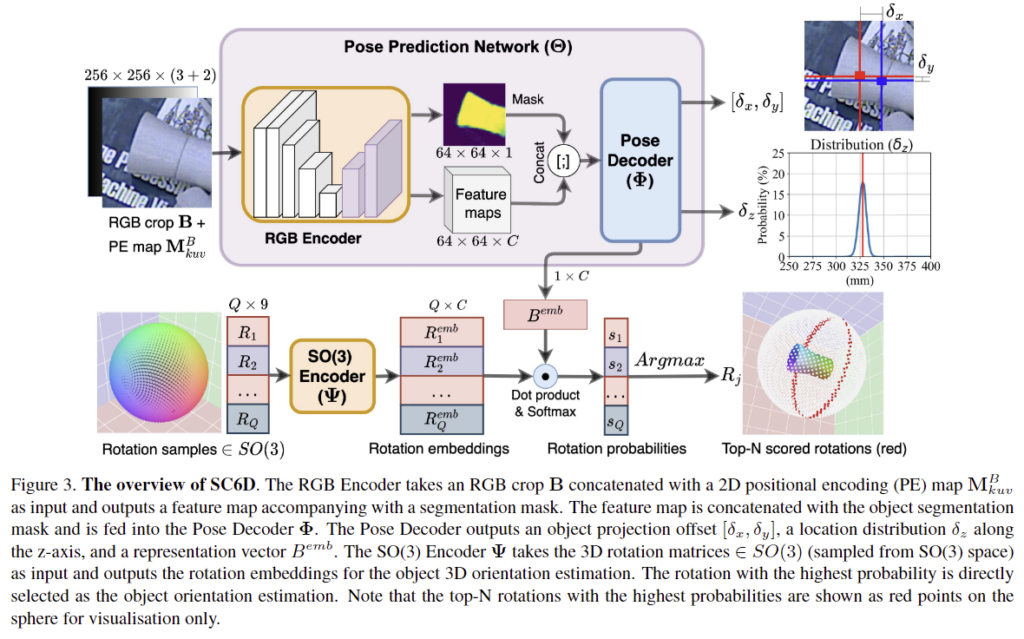
1. Learning 3D Orientation Distribution

물체의 대칭에 관한 사전 지식이 있더라도 대칭 객체의 3D 방향을 추정하는 것에는 어려움이 있습니다. 본 논문에서는 객체의 대칭을 명시적으로 처리하는 것을 피하기 위해 (사전지식을 이용하지 않기 위해) 3D 방향을 예측하기 위한 SO(3) 인코더를 학습하는 것을 제안합니다.

객체 영역에 대한 crop 이미지 \mathbf{B}가 주어졌을 때, 객체의 3D 방향 분포를 학습하기 위해 아래의 식1로 나타낼 수 있으며,

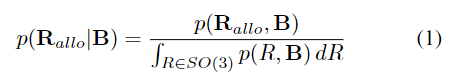
이를 근사시키면 아래의 식 2로 표현할 수 있습니다.

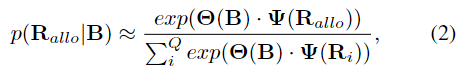
이때, \mathbf{R}_{allo}는 외부중심의 방향, \{ \mathbf{R}_i \}^Q_{i=1}∈SO(3) 은 rotation sample, \Theta는 객체의 pose를 예측하는 네트워크, \Psi는 SO(3) 인코더(Figure 3에서 확인 가능)를 의미합니다.

2. Scale-Invariant Location Estimation

\mathbf{\bar{P}}^B와 \mathbf{\bar{P}}^X는 각각 객체에 대해 crop된 영역 \mathbf{B}와 원본 이미지 \mathbf{X}로 3D 원점의 투영 좌표를 나타내며, 아래의 공식으로 관계를 정의할 수 있습니다.

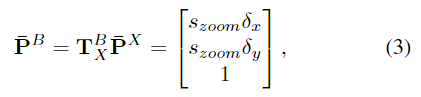
• \mathbf{T}^B_X∈R^{3x3}: 원본 이미지 좌표계 \mathbf{X}에서 crop 이미지 \mathbf{B}로의 변환
• ( \delta_x, \delta_y )는 객체가 \mathbf{B}의 중심에 투영된 ~에 비례하는 offset객체 원점의 비율

변환 관계 \mathbf{T}^B_X는 2D 변환 및 스케일링 연산으로 볼 수 있으며, 아래의 식으로 정의됩니다.

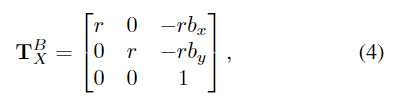
• r = s_{zoom}/s_b: 원본 box 크기인 s_b에서 대상 크기 s_{zoom}까지의 스케일링 factor
• ( b_x, b_y) : 원본 이미지의 bounding box 중심

따라서 새로운 카메라 intrinsic matrix \mathbf{K}_B는 아래의 식 5를 통해 구할 수 있습니다. (이미지의 객체 중심 crop을 거치며 intrinsic matrix에도 변화를 준 것입니다.)

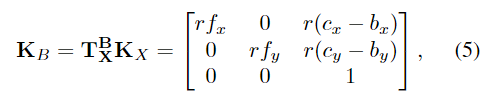
• \mathbf{K}_X: 원본 이미지의 intrinsic matrix

2D 위치 인코딩 (PE) map은 crop이미지 영역에 대한 그리드 \mathbf{G}_{uv}를 이용하여 \mathbf{M}^B_{kuv} = \mathbf{K}^{-1}_B \mathbf{G}_{uv} 구합니다.

이제, 객체의 원점으로부터 \mathbf{B}로의 객체의 원점 투영은 \mathbf{K}_B(\mathbf{R}P_o+\mathbf{t})=t_z\mathbf{\bar{P}^B}, P_o=[0,0,0]^T가 됩니다. z축에 대한 translation 값 t_z는 RGB 이미지에서 객체의 크기에 직접적으로 영향을 주는 값이지만, crop 과정을 거치며 s_zoom으로 변경됩니다. 이를 위해 크기가 조정된 객체 중심 영역 \mathbf{B}와 같이 객체 z축 이동에 대해 크기 불변한 매개변수 \delta_z \ t+z /r를 추정합니다. 따라서, 물체 좌표계에서 카메라 좌표계로의 3D 변환은 \mathbf{t} = \ r\delta_z\mathbf{K}^{-1}_B\mathbf{\bar{P}}^B가 됩니다.

\delta_z를 직접 regression 하는 대신 z-축의 translation 예측은 균일하게 이산화 된 z 축을 따라 K개의 bin으로 개체의 위치 d_i = d_l + (d_u - d_l) * i/K를 구합니다. 이때, d_u, d_l은 \delta_z의 upper/lower bound가 됩니다.

3. Recovering the Egocentric Orientation

본 논문은 외부 중심의 방향을 추정하는 방식으로, 일반적인 6D Pose estimation의 객체 중심의 방향을 구하는 과정이 필요합니다. 이를 위해 \mathbf{R} = \mathbf{R}_c\mathbf{R}_{allo} 식을 이용하여 객체 중심의 rotation \mathbf{R}을 구하기 위해 \mathbf{R}_c를 구합니다. \mathbf{R}_c는 ray \mathbf{o}_{ray} = \mathbf{K^-1_{B}\bar{P}^B}에서 물체의 원점과 카메라 광축까지의 3D 회전을 추정하여 얻을 수 있으며 아래의 식으로 표현할 수 있습니다.

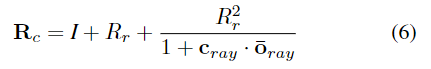
• \mathbf{I}: 단위 행렬
• \mathbf{\bar{o}_ray}=\mathbf{o_ray / |o_ray|}: 정규화 된 단위 벡터
• \mathbf{R}_r: skew-symmetric 행렬

4. Loss Function

InfoNCE loss를 적용하여 3D 방향에 대한 representation 분포를 학습한다.

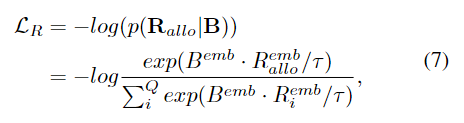
• B^{emb}: 정규화된 representation vector
• R^{emb}_allo: GT 외부 중심의 방향 \mathbf{R}_{allo}는 정규화된 embedding representation

또한, (\delta_A,\delta_y) 예측을 학습하기 위해 L1 loss를 사용하고, 물체의 z축 위치는 classification으로 해결하기 위해 focal loss를 적용합니다. 이 두가지 loss를 아래의 식 8로 정리할 수 있습니다.

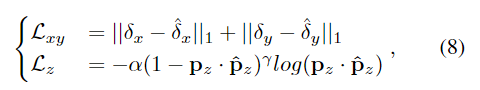
• \hat{}: GT
• \mathbf{p}_z: 네트워크의 출력에 대한 확률

loss들은 가중합을 통해 최종 loss를 구하게 됩니다.

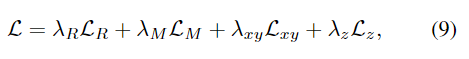
Experiments

T-LESS, YCB-V, ITODD 데이터 3가지에 대한 실험을 통해 SC6D를 평가하였습니다.

Comparison to the SOTA

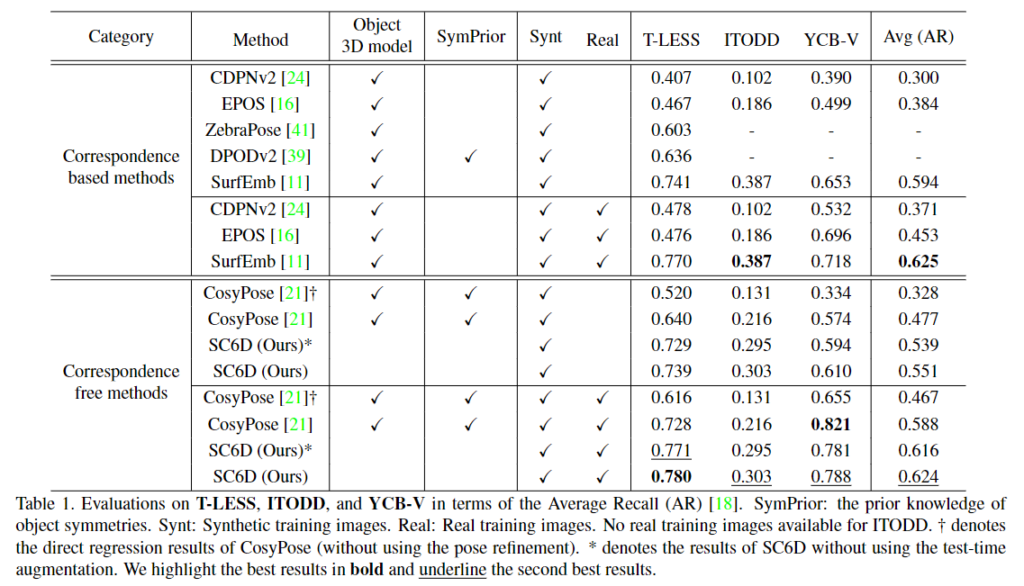
• 아래의 Table 1에 AR 성능을리포팅하였으며, 전반적으로 SC6D는 객체의 3D 모델이나, 객체의 대칭에 대한 사전 지식을 사용하지 않고도 타 방법론과 비슷한 성능을 달성하는 것을 확인할 수 있습니다.
• SurfEmb(SOTA 알고리즘)와 비교
  • 특히, 합성 PBR 이미지만 사용하여 학습할 경우 SC6D는 T-LESS에서 73.9%, ITODD에서 30.3%, YCB-V에서 61.1%의 AR을 달성하였으며, 이는 SurfEmb를 제외한 다른 베이스라인 방법론들보다 더 좋은 성능을 나타냅니다.
  • fine-tuning을 수행할 경우, SC6D의 성능이 개선되었으며, SurfEmb와 비교하였을 때 T-LESS에서 1.0%, YCB-V에서 7.0% 성능 개선이 이루어짐을 확인할 수 있습니다.
  • 또한, SC6D는 추론과정에 약 30ms가 소요되었으며, SurfEmb는 시간이 많이 소요되는 PnP-RANSAC 과정으로 인해 약 2200ms의 시간이 소요되는 것을 실험적으로 확인하였다고 합니다.
• correspondence-free 방법론 비교
  • correspondence-free 방식인 CosyPose와 비교하였을 때 전반적으로 좋은 성능을 보이는 것을 확인하였습니다.
  • (CosyPose-coarse는 초기 pose regression 네트워크를 포함하며, CosyPose-refiner는 pose refinement 네트워크를 포함)
  • Test-time Augmentation을 사용하지 않을 경우, SC6D가 CosyPose-coarse보다 성능이 크게 개선되는 것을 확인하였으며, CosyPose에 refinement를 포함할 경우에도 YCB-V 데이터를 제외한 다른 데이터에서 SC6D가 성능을 능가하는 것을 확인할 수 있습니다.

• 아래의 Figure4는 T-LESS에 대한 정성적 결과로 예측된 결과를 이미지에 그린 결과입니다.

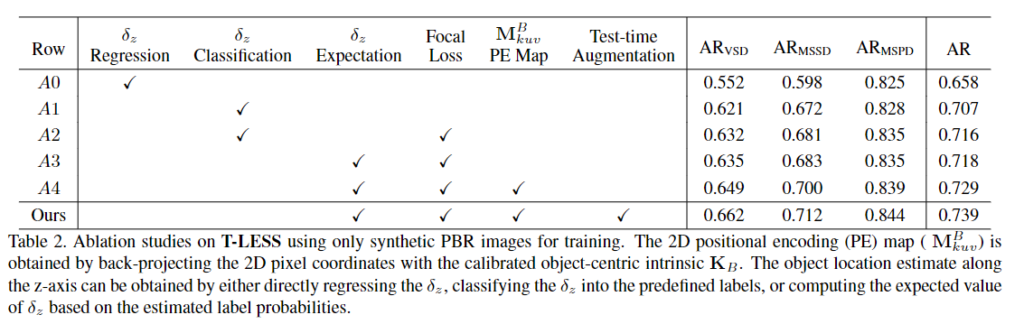
Ablation Studies

• Regression vs. classification
  • classification 기반의 방식은 regression 기반의 방식에 비해 약 5%의 성능 개선이 이루어짐을 확인할 수 있습니다.(A0&A1)
  • 이를 통해 classification 기반의 방법론의 효과를 확인할 수 있으며, focal loss를 활용할 경우 1%의 성능 개선이 이루어짐을 실험적으로 보입니다.(A1&A2)
  • 또한, 연속적인 z축의 translation을 추정함으로써 성능 개선이 이루어짐을 확인하였습니다.(A2&A3)
• 2D positional encoding map
  • 카메라의 intrinsic 파라미터를 이용하여 역투영된 2D 위치의 encoding map을 이용하므로써 1.1% 성능이 개선됨을 확인할 수 있습니다.(A3&A4)