안녕하세요, 스물한 번째 X-Review입니다. 이번 논문은 2007년도 TPAMI에게재된 Stereo processing by Semi-Global matching and Mutual Information 논문으로 딥러닝 기반이 아닌 전통적인 방식으로 stereo matching을 수행하는 알고리즘입니다. 그럼 바로 리뷰 시작하겠습니다 !

1. Introduction

Stereo Matching은 서로 다른 시점의 stereo image가 있을 때 기준 영상에서의 한 point에 대한 동일한 point를 타겟 영상에서 찾는 과정으로, 일반적인 stereo matching 파이프라인은 아래와 같습니다.

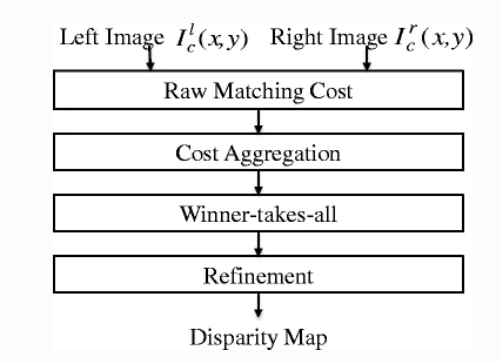
1. Matching cost(매칭 비용) 계산
2. Cost(비용) Aggregation
3. Disparity Computation (winner-takes-all)
4. Refinement

순입니다.

가장 먼저 수행되는 매칭 비용 계산이란, 두 영상의 유사도를 pixel 단위로 측정하는 것을 의미합니다. 이 때 pixel 단위로 계산된 matching cost를 하나의 volume으로 쌓은 것을 cost volume이라고 하며, 두 번째 단계인 cost aggregation에서 cost volume의 정보를 aggregate해 계산된 cost 정보의 신뢰도를 높입니다.

cost aggregation 과정에서 신뢰도를 높인다는 것이 무슨말이냐 함은, cost volume 상에서는 실제로 서로 대응되는 픽셀들 사이에서 계산된 cost와 서로 대응되지 않은 pixel들 사이에서 계산된 cost의 차는 크지 않지만, cost aggregation 과정에서 주변에 대응된 pixel들의 cost를 합한 것과 대응되지 않은 pixel들의 cost를 합산한 것의 cost 차이는 커질 것이기 때문에 더 정확한 대응 pixel을 찾을 가능성이 높아지는 것을 의미합니다.

cost aggregation 과정 이후에는 aggregation된 cost volume에서 disparity를 계산하게 됩니다. 이 때 추정된 disparity는 카메라 초점 거리와 두 카메라 사이 거리인 baseline 정보를 통해 depth를 추정할 수 있게 되겠죠.

오늘 리뷰할 논문은 전통적인 stereo matching 방법론인 Semi-Global Matching(이하 SGM)에 대해 제안하는 논문입니다.

2. Semi-Global Matching

2-1. Pixelwise Matching Cost Calculation

스테레오 매칭 알고리즘의 첫 단계인 matching cost를 계산하는 과정에 대해 살펴보도록 하겠습니다. 보통 입력으로 들어오는 두 이미지는 rectification이 된 이미지이며, 두 이미지 중 기준으로 삼을 이미지를 base 이미지, 매칭할 이미지를 matching 이미지라고 칭합니다. 두 이미지가 rectification 되었기 때문에 base 이미지 내 한 픽셀 p에 대한 매칭점 q를 matching 이미지에서 찾고자 한다면, 그 base 이미지 픽셀 p에 대한 match 이미지의 epipolar line을 돌며 찾으면 되겠죠. 이를 아래 수식과 같이 나타낼 수 있겠습니다.

q = e_{bm}(p, d)

여기서 e_{bm}는 epipolar line이며, d는 disparity에 해당합니다.

pixelwise로 cost를 계산하는 한가지 방법으로는 Birchfield와 Tomasi가 제안한 방식이 있습니다. 단순하게 cost C_{BT}(p, d)는 base 이미지의 픽셀 p와 matching 이미지의 픽셀 q = e_{bm}(p, d)사이의 intensity 차이를 절대값을 씌운 것으로 계산됩니다. 다시 말해 에피폴라 라인 선상을 돌면서 픽셀 p와의 intensity 차이가 가장 작은 부분을 matching point로 삼는다는 의미입니다.

또 다른 방식으로는 본 논문에도 적혀있듯이 Mutual Information 기반으로 matching cost를 계산하는 방식이 있습니다. 이 Mutual Information은 두 사건 사이의 연관성을 의미하며 식1과 같이 두 이미지의 엔트로피와 joint 엔트로피로 정의됩니다.

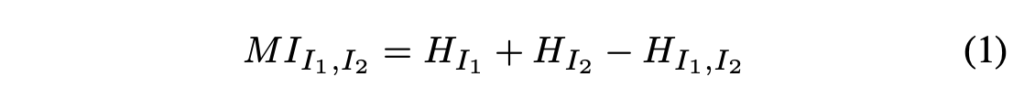
• H_{I_1} : 이미지 1에 대한 엔트로피
• H_{I_2} : 이미지 2에 대한 엔트로피
• H_{I_1, I_2} : 이미지 1, 2에 대한 joint 엔트로피

이 엔트로피들은 이미지들 intensity의 확률 분포 P에 의해 계산됩니다.

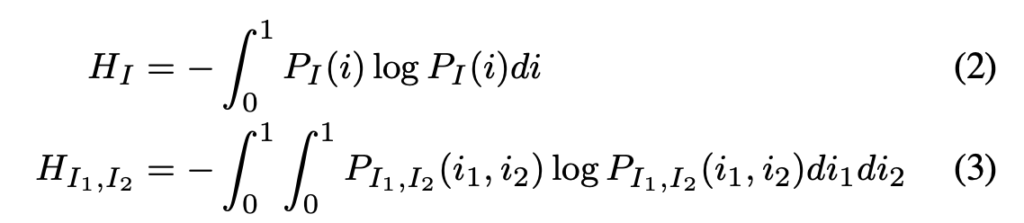
두 이미지가 잘 정합된 경우를 생각해본다면, joint 엔트로피인 H_{I_1, I_2}는 낮은 값을 갖겠죠. 한 이미지가 다른 이미지에 의해 예측될 수 있기 때문에 정보량이 낮기 때문입니다. 그럼 결국 큰 MI 값을 갖게 될 것입니다.

하지만 식 1같은 경우 전체 이미지에 적용되므로 pixel-level로 matching cost를 계산하지 못합니다. 이에 대해 2003년에 Kim et al.은 joint entropy의 계산을 Talyor expansion을 사용해 pixel level로 변환해 내었습니다. 결과적으로 이 joint 엔트로피 H_{I_1, I_2}는 아래 식처럼 표현됩니다.

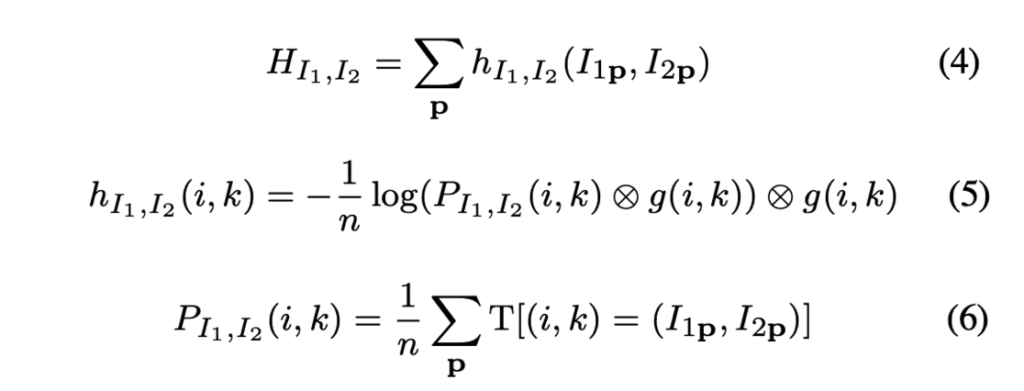
이후에 각 이미지에 대한 엔트로피도 정리해나가면 최종적으로 Mutual Information을 통해 matching cost를 구하는 식은 다음과 같이 도출됩니다.

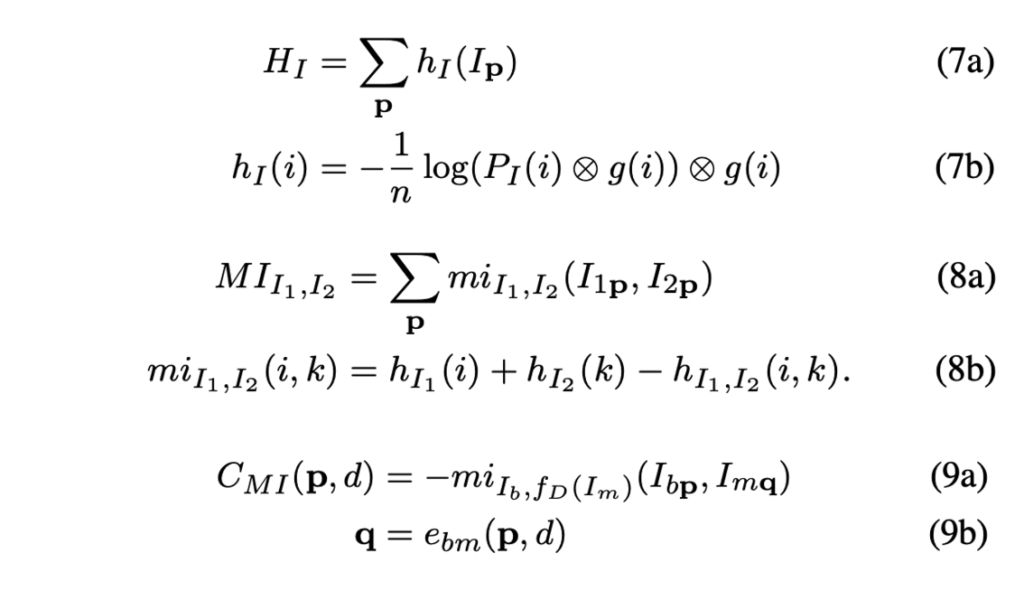
2-2. Cost Aggregation

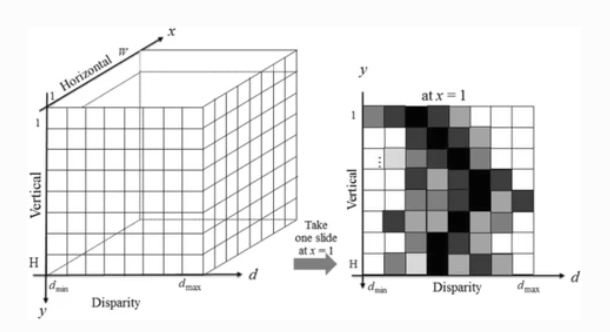
앞에서 설명한 Mutual Information 기반으로 pixel별 matching cost를 계산하게 된다면 위 그림과 같은 3D cost volume이 생성됩니다. cost volume이란 단순히 계산한 cost를 쌓은 것입니다. 우측에 2D 이미지는 cost volume을 x축으로 slice하여 x=1인 경우의 slice를 보여주고 있습니다. 무튼 이 cost volume을 가지고 바로 dispairty를 추정하기보다 이 cost volume을 가지고 aggregation을 수행하여 잘못된 matching을 할 가능성을 줄이는 작업을 수행합니다. 이때, 제약 조건으로 smoothness가 추가되는데 이는 한 pixel과 그의 이웃 pixel의 disparity를 유지하도록 하여 부드러운 disparity map을 생성하기 위함입니다. 즉, disparity가 변하기 위해서는 패널티를 부과했을 때 이 패널티를 부과한 cost가 dispairty를 유지하도록 하였을 때의 cost보다 작아야 합니다.

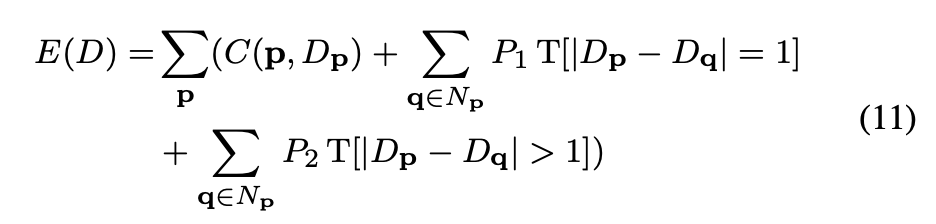
• D : disparity
• P_1, P_2 : 패널티 1, 2

이를 기반으로 에너지 함수를 정의해본다면 위의 식이 됩니다. 첫번째 항은 disparity D에 대한 모든 pixel의 matching cost 합을 의미하며, 두번째 항은 픽셀 p의 이웃 픽셀인 q에 대해 disparity가 1차이 나는 경우 패널티 P_1를 추가하고 있으며, 세번째 항은 비슷하게 pixel p와 이웃 픽셀 q 사이의 dispairty가 크게 변하는 경우에 P_1보다 더 큰 패널티인 P_2를 추가하게 됩니다.

그럼 이제 stereo matching 문제는 이 에너지 함수 E(D)를 최소화하는 disaprity D를 찾는 것으로 정의해볼 수 있겠습니다. 이 에너지 함수를 최소화하는 경우 모든 pixel을 고려 해야 하는 global minimization 문제에 해당하는데, 이 global minimatiation은 2D 상에서 NP-Complete Problem이 됩니다. 이는 연산해야 하는 수가 지수함수적으로 증가하는 문제라는 의미이며, 간단히 말해 최적의 disparity를 찾는 과정이 굉장히 복잡하다는 것입니다.

이런 NP-Complete Problem을 해결하기 위해 저자는 2D global minimization을 모든 방향을 고려하는 1D의 minimization 문제로 푸는 cost aggregation 방식을 제안하게 됩니다. 이는 각 방향에 대해 따로 따로 cost를 계산하고 이를 조합해 최종적인 cost를 구하는 것으로 볼 수 있습니다. 이 1D aggregation cost S(p, d)를 계산하는 방법은 해당 pixel p에서 disparity가 d인 모든 1D minimization cost path의 cost를 더함으로써 계산됩니다. 이 경로들의 cost를 모두 더해 S(p, d)를 구할 수 있게 되고, 이 S(p, d)가 해당 pixel p에서의 disparity d에 대한 최종 cost를 의미하게 됩니다.

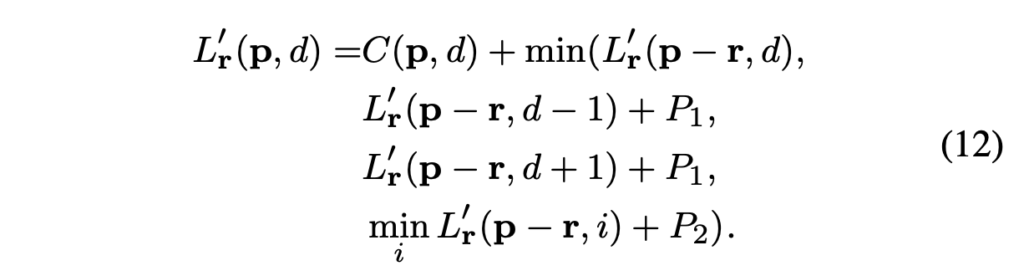
• L^’_r(p, d) : disparity d에서 pixel p의 minimum cost path 값
• r : direction
• P_1, P_2 : 패널티 1, 2

기존 에너지 함수를 1D aggregation 방식으로 변경한 식은 위 식과 같습니다. pixelwise matching cost C같은 경우 앞장에서 언급한 BT(Birchfield와 Tomasi가 제안한 방식)과 Mutual Information을 이용한 방식 중 하나로 계산할 수 있겠습니다.

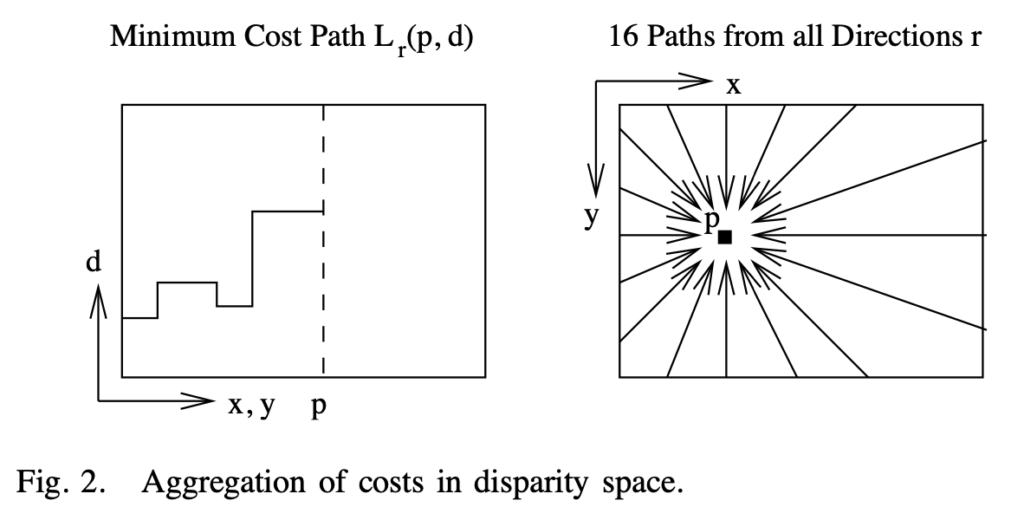
본 논문에서는 방향 r을 16가지로 정하였으며, 이는 fig2의 우측 그림에 나타난 것과 같습니다. r같은 경우 unit vector로 표현이 되며, 예로 r이 (1, 0)인 경우를 생각해본다면, 아래 그림과 같겠습니다.

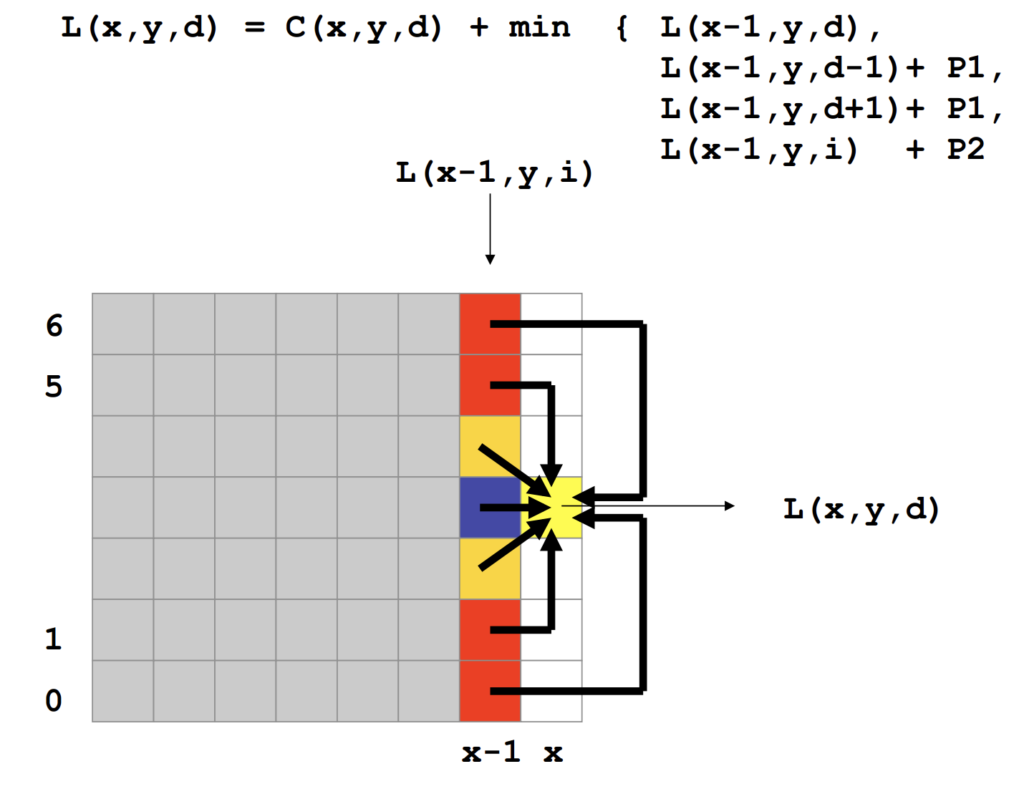
추가로 식 12를 통해 구한 minimum cost path값인 L’의 경우 path를 따라 계속 증가할 수 있습니다. 이는 cost가 계속 누적되어 매우 큰 값으로 이어질 수 있다는 문제가 있다고 하는데,,, 저자는 이에 대해 이전 pixel의 최소 path cost를 전체 항에서 뺌으로써 path의 값이 지속적으로 증가하지 않도록 조정하였습니다.

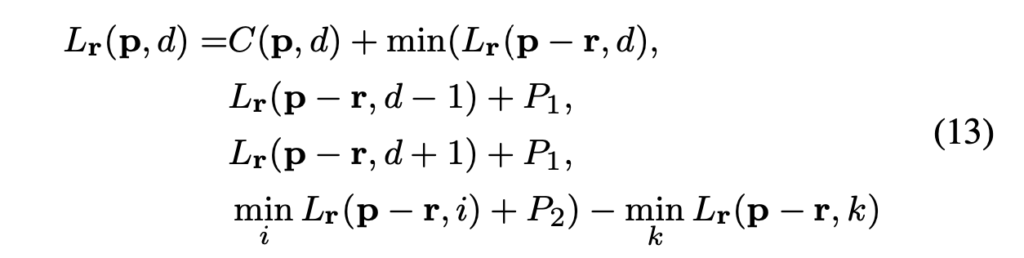
식 13을 보면 마지막 항이 추가된 것을 확인할 수 있고, 값이 지속적으로 증가하는 것을 막아주는 부분에 해당합니다. 이렇게 이전 pixel의 minimum path cost를 뺌으로써 path의 값을 유지할 수 있으며, 이렇게 빼는 값은 모든 disparity에 대해 상수값이기 때문에 최소값의 위치는 변경되지 않는다고 합니다.

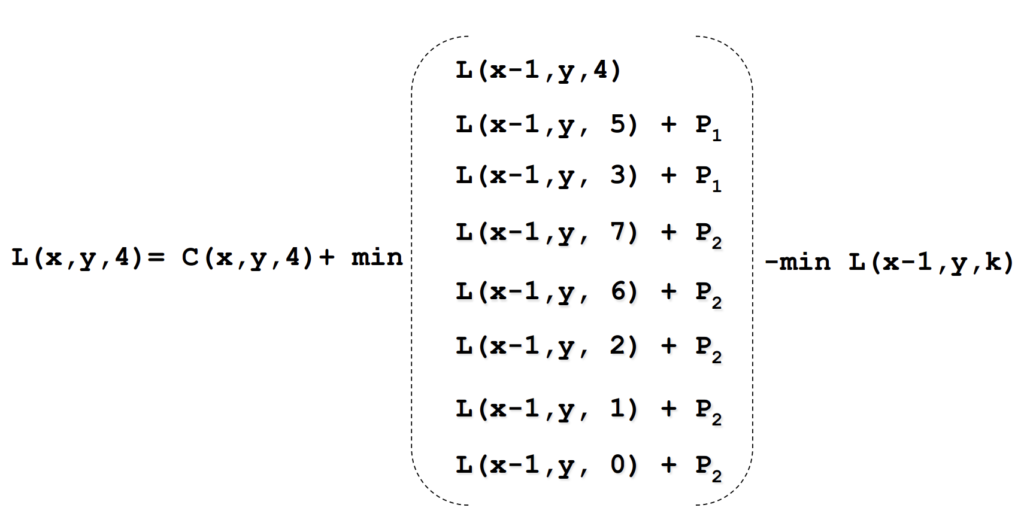
이렇게 수정된 식에서 disparity가 4이고, r이 (1, 0)일 때의 L_r(p, d) 값을 구한다면 아래 식을 계산하면 되겠죠 ! disparity 차이가 1인 경우에는 패널티 1을, 그보다 더 차이나는 경우에는 패널티 2를 더해줍니다. 이 각각의 값 중 최소값만을 선택해 더하게 되죠. 이는 앞에서 언급한 것처럼 smoothness 제약을 하는 부분에 해당합니다. (이웃 픽셀과의 disparity 변화를 유지하기 위한) 마지막 항은 값이 지속적으로 증가하는 것을 막기위한 항에 해당하겠죠.

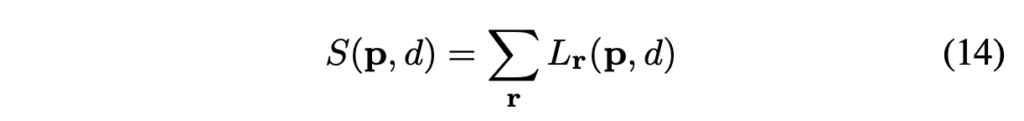
최종적으로 path의 cost를 합산하게 되면 pixel p에서 disparity d에 대한 cost aggregation 값이 나오게 됩니다. . . .

2-3. Disparity Computation

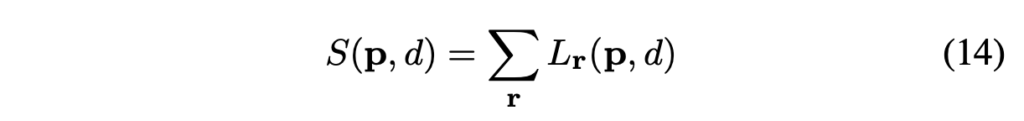
최종적으로 cost aggregation 과정에서는 위 식을 통해 각 pixel p에 대해 disparity 별로 cost aggregation한 cost 값을 얻어 냈었습니다. pixel p에 대한 disparity는 단순하게 disparity 별 S(p, d)값이 가장 작은 d를 선택함으로써 구해지게 됩니다 !

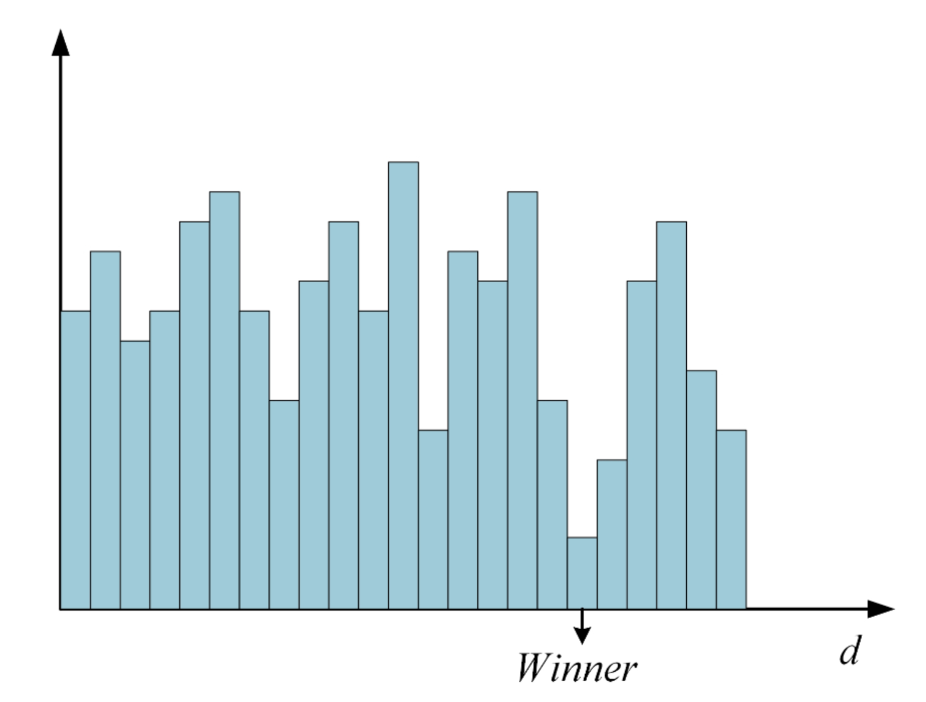
다시 말해 한 pixel p에서 여러 disparity에 대해 cost aggregation한 값이 위와 같이 나온 경우가 있다면, 가장 값이 작은 곳에서의 disparity가 그 pixel p에 대한 disparity로 선택되게 되는 것입니다. 그래프에서 가로축은 disparity 세로축은 cost aggregation한 값입니다. 이렇게 가장 작은 값의 disparity를 선택하는 것을 winner takes all이라고 합니다.

3. Experimental Results

middlebury stereo 이미지를 가지고 실험을 진행했으며, 위에 있는 이미지가 스테레오 이미지 쌍 중 왼쪽 이미지입니다. 좌측부터 순서대로 16, 32, 64, 64의 dispairty 범위를 갖습니다.

disparity map은 위와 같습니다. 앞에서 설명드린 베이직한 SGM이 위의 결과에 해당하며, 아래 정성적 결과는 C-SGM으로 disparity를 다 구한 후, disparity refinement (Intensity Consistent disparity selection) 과정을 거친 SGM에 해당합니다. refinement를 거친 C-SGM의 경우 세번째 사진에서 곰돌이의 팔 부분을 잘 복원해내는 것을 확인할 수 있습니다. 반면, 같은 사진의 동일한 부분에서 SGM은 foreground의 disaprity를 생성하고 있습니다.

정량적인 결과는 아래 표 1에서 확인할 수 있습니다.

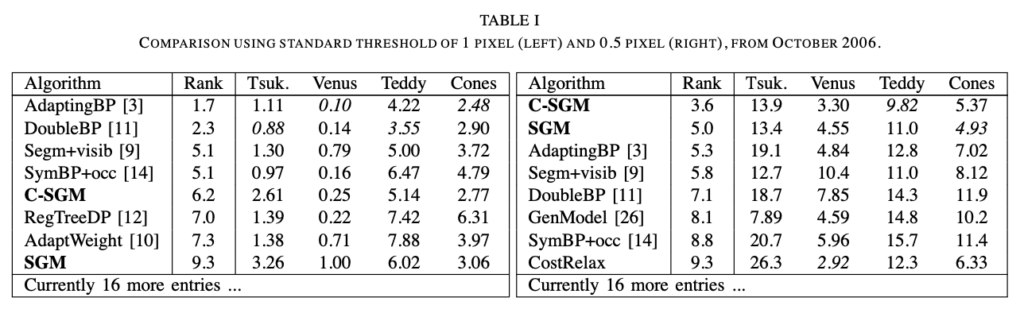
좌측 표는 gt disparity와 예측한 dispairty간의 차이가 1px 이상인 것들에 대한 에러율, 우측은 0.5px 이상인 것들에 대한 에러율을 측정한 것입니다. 당연하게도 disparity refinement 과정을 거친 C-SGM의 경우가 SGM에 비해 더 좋은 결과를 보입니다. 이는 texture가 없는 배경 영역에 대해 recover를 해주는 refinement를 적용하였기 때문이죠. 또, 신기하게도 1px가 threshold인 경우에는 두 알고리즘이 막 좋은 성능을 보이진 않았지만, 0.5로 설정한 경우에는 가장 좋은 성능을 보입니다.

마지막으로 본문에는 언급하지 않았지만, 여러 후처리 방식에 대한 효과를 보여주는 사진을 가져왔습니다. matching cost를 계산하고, cost를 aggregation하고, 이에 대해 disparity를 계산한 뒤 어떠한 후처리를 거치지 않은 basic SGM의 정성적 결과는 Fig 13-(a)와 같습니다. (b)가 peak filtering을 거친 것이고, (e)가 intensity consistent selection을 한 것으로 위 정량적 결과 표예서 C-SGM에 해당하는데, 육안으로 보기에는 (a)와 별 차이는 없어보입니다. . . 🤨 (g)같은 경우는 interpolation을 수행하여 dispairty 이미지를 보다 부드럽게 만든 결과입니다.