제가 이번에 리뷰할 논문은 6D Pose Estimation에 self-supervised 방법론을 적용한 논문입니다. 6D Pose Estimation에서 self-supervised 방식을 어떻게 적용하였는 지 궁금하여 리뷰하게 되었습니다. 이제 리뷰 시작하겠습니다!
Introduction
6D Pose Estimation task는 학습을 위해 다양한 view point에서 촬영된 데이터가 필요하다는 문제가 있으며, 6D 정보( translation & rotation )에 대한 GT를 생성에 많은 시간과 비용이 들어 대용량 데이터를 생성하기 어렵습니다. 이러한 문제를해결하고자 기존 연구들은 (1)합성 데이터를 만들거나 (2)self-supervised 학습 방식을 도입하여 문제를 해결하고자 하였습니다. 그러나 합성 데이터를 만들어 학습을 수행할 경우 실제 데이터와 합성 데이터 사이의 도메인 차이가 존재한다는 한계가 있으며, self-supervised 학습 방식의 경우 6D Estimation task에서는 depth 정보나 픽셀 수준의 segmentation mask 정보와 같이 추가적인 정보가 필요하다는 한계가 있습니다. 본 논문은 이러한 한계를 극복하는 것을 목표로 연구를 수행하였으며, depth나 2D annotation 정보에 의존하지 않는 self-supervised 학습 프레임워크에 대한 연구를 수행하였습니다.
기존 6D Pose Estimation 연구들은 pose estimation 과정 뿐만 아니라 refinement를 통해 pose 정보를 정교화하는 과정에 대한 연구도 수행되었으며, 본 논문은 후자인 refienement 과정에 집중하였습니다. 저자들은 합성 데이터를 이용하여 학습한 모델을 이용하여 대략적인 초기 pose를 구하고, 이후 예측된 pose를 이용하여 reference 이미지를 랜더링하여 생성한 뒤 pseudo label과 실제 데이터를 비교하는 방식으로 refinement를 수행합니다. 그러나 6D에 pseudo label을 이용하는 전략은 pseudo label을 생성하는 방식과 노이즈가 포함된 후보로부터 고품질의 label을 추출하는 방식에 대하여 연구가 필요하며 아직 해결되지 못한 문제입니다.
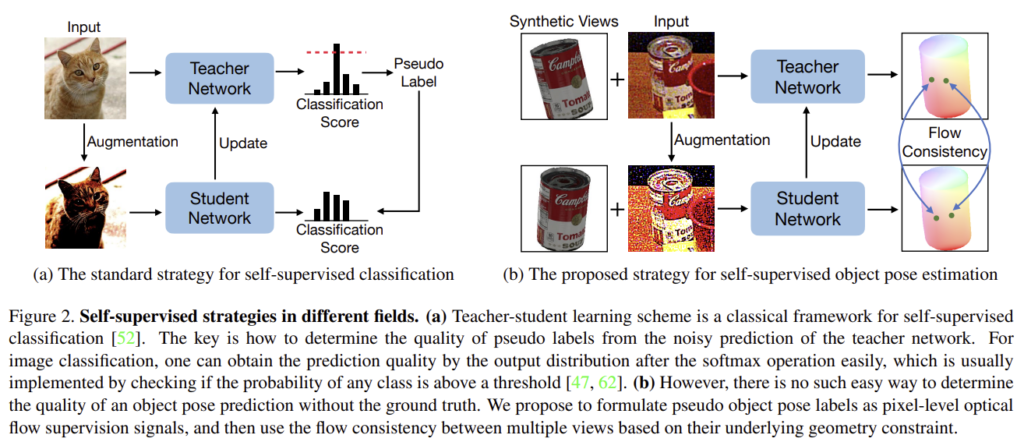
저자들은 pseudo 6D pose label을 픽셀 수준의 flow 신호를 이용하는 문제로 정의하였으며, 어노테이션 없이 기하학적 정보를 알려주는 학습 프레임워크를 제안하였습니다. 초기 pose 주변의 pose값으로 여러 이미지를 렌더링하여 구한 뒤, 실제 이미지와 서로 다른 view의 합성 이미지를 비교하여 flow의 일관성을 통해 기하학적 제약을 주도록 학습합니다. 또한, 고품질의 flow label을 판단하기 위해 flow의 일관성을 이용합니다. 저자들은 6D에서 가장 많이 사용되는 3가지 밴치마크(LINEMOD, Occluded-LINEMOD, YCB-Video)에 대하여 평가를 진행하고, self-supervised 기반 6D 방법론의 SOTA 방법론들과 비교하였을 때 뛰어난 성능을 보임을 확인하였습니다.
본 논문의 contribution을 정리하면
- self-supervised 6D Pose Estimation을 위해 teacher-student 방식의 고품질의 pseudo label을 선택하는 방법론 연구
- 다양한 view에서 기하학적 제약을 포함하는 flow의 일관성을 기반으로 방법론 제안
- 추가적인 정보에 의존하지 않고 self-supervised 방식의 6D Pose Estimation을 통해 추가적 정보를 이용하는 기존 SOTA 방법론보다 좋은 성능을 실험적으로 보임
Approach
본 논문에서는 self-supervised 6D Pose Estimation을 위해 주어진 RGB 이미지 데이터와 대상 3D model을 이용합니다. 3D model을 이용하여 합성 데이터를 생성하여 기존에 연구된 6D Pose Estimation 네트워크를 학습합니다. 이후 self-supervised 방식의 pose refinement 프레임워크를 제안하여 기하학적 제약을 기반으로 flow 일관성을 통해 문제를 해결하는 방법을 제안합니다.
1. Framework Overview
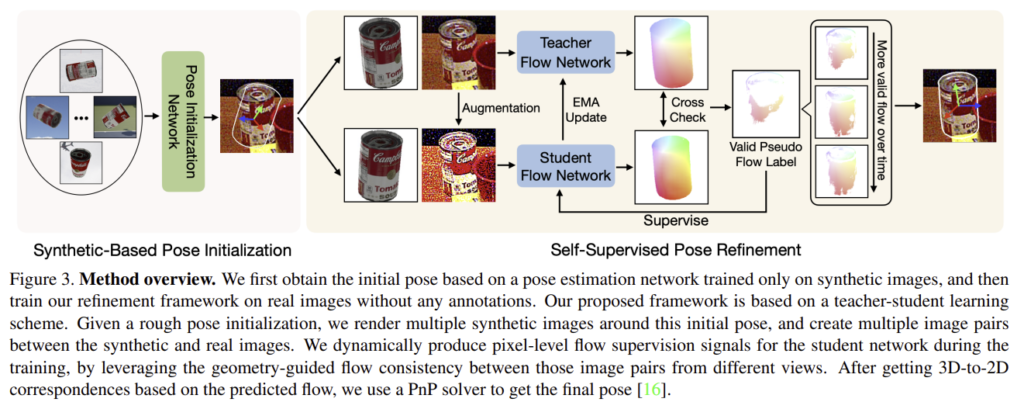
해당 논문은 동일 구조를 가지고 서로 다른 가중치를 가지는 teacher-student 구조를 이용합니다. 학습 과정에 teacher 네트워크를 통해 특정 기준을 만족하는 예측치를 이용하여 pseudo labeld에 대한 학습을 통해 student 모델을 학습합니다. 이후 EMA(exponential moving average) 방식을 이용하여 teacher 가중치를 업데이트 하게 됩니다. EMA는 아래의 식(1)을 통해 구하며, 이때 \mathbf{W}_t , \mathbf{W}_s 는 각각 teacher와 student 모델의 가중치를 의미하며, \alpha 는 지수인자로 일반적으로 0.999입니다. 즉 teacher 모델은 student 모델의 영향을 아주 조금씩 받도록 업데이트를 수행하는 것입니다.
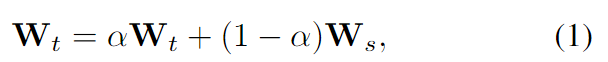
이러한 가중치 업데이트와 pseudo label 생성은 각 iteration마다 반복되며, 이는 학습이 모두 끝난 뒤 pseudo label을 생성하던 기존의 pseudo label 기반의 object pose 연구에 비해 효과적인 방식입니다.
pseudo label을 이용한 학습 과정은 위와 같으며 이제 본 논문에서 가장 집중한 문제였던, 노이즈가 포함된 후보들 중 고품질의 pseudo label을 선택하는 문제를 다룹니다. classification과 같은 task에서는 threshold를 통해 예측값이 일정 확률 이상일 경우 활용하는 방식을 채택할 수 있으나, 6D Pose Estimation에서는 GT pose가 없을 경우, 예측 pose의 품질을 평가하기가 어렵습니다. 이를 위한 해결방안을 저자들은 기하학적 제약조건에 기반한 flow consistency를 이용하여 해결하고자 하였습니다.
2. Flow Consistency across Multiple Views
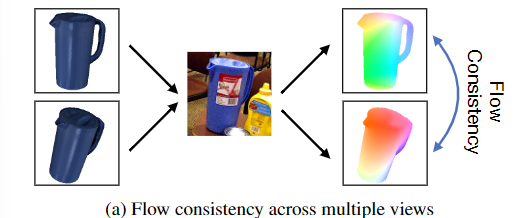
예측된 pose의 품질을 결정하는 문제를 해결하기 위해, 저자들은 object pose estimation을 2D-to-2D의 dense한 대응 관계를 예측하는 문제, 즉 optical flow 추정 문제로 공식화하였습니다. GT flow를 계산하기 위한 pose 정보가 없는 문제를 해결하고자, 예측된 초기 pose 값 주변의 pose로 여러 이미지를 렌더링하고 렌더링된 이미지와 real 이미지 사이의 flow를 예측합니다. 렌더링된 이미지와 실제 이미지는 모두 동일한 3D 모델이 2차원으로 투영된 것이기 때문에 기본 형상과 일치하는 flow 예측은 고품질의 예측값일 가능성이 높습니다. 이러한 flow consistency를 이용하여 다음과 같이 학습을 수행합니다.
먼저, GT 정보가 없는 실제 이미지 \mathbf{I}^t 가 주어졌을 때, 합성데이터를 이용하여 학습된 네트워크를 통해 초기 pose \mathbf{P}_0 를 구하고, n-1 개의 주변 pose \{ \mathbf{P}_1, ... , \mathbf{P}_{n-1} \} 를 랜덤으로 생성합니다. 이후 n개의 합성 이미지를 각 poes를 이용하여 렌더링하여 실제 이미지와 쌍을 생성합니다.
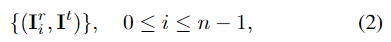
- \mathbf{I}_i^r : target pose \mathbf{P}_i 를 이용하여 렌더링한 이미지
N 개의 3D keypoint \mathbf{p}_j , 1≤ j ≤ N 를 2D로 투영시킬 경우 아래의 식(3)으로 표현이 가능하며, 이때 \lambda_{ij}^r, \mathcal{K}는 scale값과 intrinsic 파라미터 값을, \mathcal{R}_i, \mathcal{t}_i 는 각각 \mathbf{P}_i 의 rotation, translation 값을 의미합니다.
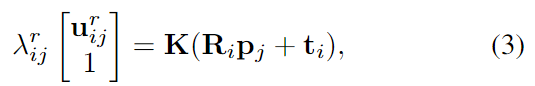
위의 식(3)을 통해 3D-to-2D ( \mathbf{p}_j ↔ \mathbf{u}_{ij}^r의 대응 관계를 구한 뒤, \mathbf{I}^t 의 GT pose \mathbf{P}^t 값은 모르지만 원근법에 따라 keypoint \mathbf{p}_j 와 2D 이미지에서 위치 \mathbf{u}_j^t 사이 관계를 암시적으로 생성합니다.
real 이미지와 렌더링된 이미지 사이의 dense한 2D-to-2D 대응 관계 \mathbf{F}_i^{r→t} 를 예측하기 위해 네트워크를 학습합니다. 아래의 식 (4)와같이 렌더링된 이미지의 keypoint 좌표가 2D flow vector \mathbf{f}_i^{r→t} 만큼 이동하면 real 이미지의 keypoint 좌표가 되어야 한다는 기하학적 제약을 주어 학습을 하게 됩니다.
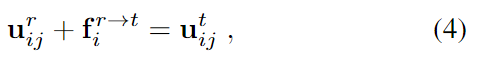
실제 GT keypoint의 위치는 모르지만, n개의 view로 렌더링된 이미지에서 구한 keypoint 좌표들이 각 flow만큼 이동할 경우 \{ \mathbf{u}_{ij}^{r} + \mathbf{f}_i^{r→t} \}는 3D keypoint \mathbf{p}_j의 2D 이미지의 위치와 동일하다는 기하학적 제약 을 이용한 것으로, 현재 픽셀의 flow 예측값이 유효한 pseudo label인지를 판단하기 위해 \mathbf{u}_{ij}^{t} 의 표준 분산값을 이용합니다. 구한 분산이 임계값 \tau 이내인지를 통해 pseudo label의 유효성을 판단하며, 유효한 label로 판단될 경우 teacher 네트워크에서 얻은 flow 예측값을 이용하여 student 네트워크를 학습합니다. loss 함수는 아래의 식(6)으로 정의되며,
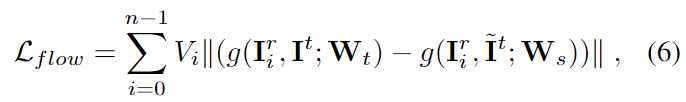
- g: flow network
- \mathbf{W}_t, \mathbf{W}_s : teacher, student의 가중치
- \tilde{\mathbf{I}}^t 는 real 이미지에 augmentation을 적용한 이미지
- V_i: 유효한 픽셀 영역에 대한 mask
3. Flow-Guided Photometric Consistency
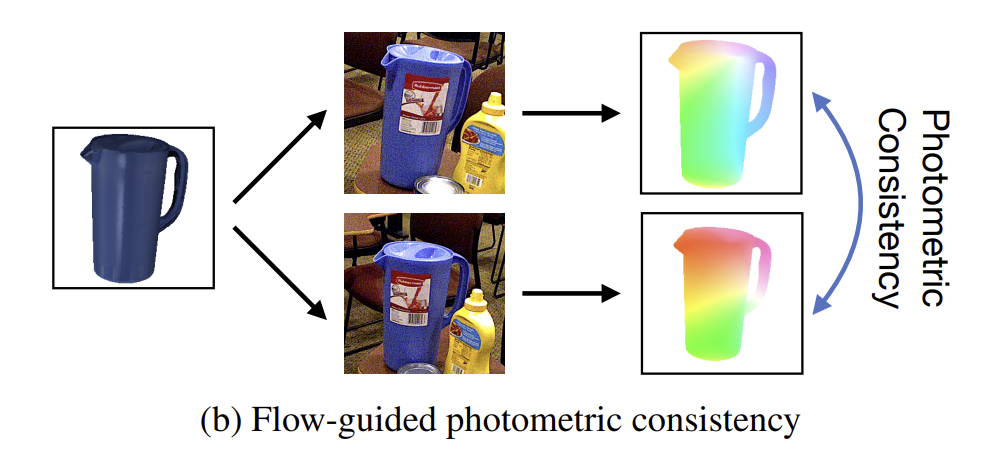
2절은 합성 view와 real input 사이의 consistency를 이용하였으며, 해당 절에서는 여러 real 입력 값 사이의 consistency를 이용합니다. 저자들은 2D로 투영된 3D keypoint가 유사한 texture를 가져야 한다는 가정에서 시작하였습니다. texture 에 대한 이러한 가정을 photometric consistency로 공식화하면 다음과 같습니다.
실제 이미지 \mathbf{I}^t 와 초기 pose \mathbf{P}_0 가 주어졌을 때, m개의 real 이미지를 무작위로 찾아 m개의 이미지 쌍 \{ (\mathbf{I}_0^r, \mathbf{I}^t_k) \} , 1≤ k ≤m 을 생성합니다.
이후 두 이미지를 teacher network로 입력하여 3D keypoint의 2D 이미지의 위치를 추정합니다.
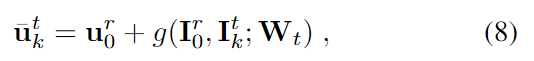
- \bar{\mathbf{u}}^t_k : 점 \mathbf{u}^r_0 의 \mathbf{I}^t_k 이미지에서 예측된 2D 위치 값
동일한 3D keypoint가 2D 이미지 위에서 유사한 texture 정보를 가질 것으로 가정하였으므로 이에 대한 loss를 아래의 식(9)로 정의합니다.
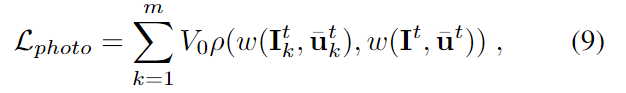
이때 w 는 새로운 픽셀 위치에 따라 이미지를 왜곡하는 연산함수이며, \rho 는 photometric 오차를 측정하기 위해 일반화된 함수, \bar{\mathbf{u}}^t 는 student의 예측값을 의미합니다.
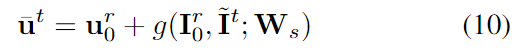
이렇게 구한 flow consistency와 photometric consistency는 가중합하여 최종 loss를 구하게 됩니다.
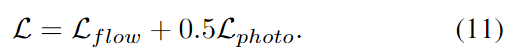
위의 최종 loss를 이용하여 student 모델을 학습하며, teacher 네트워크는 식(1)을 따라 EMA 방식으로 업데이트를 수행합니다.
Experiments
Dataset and Evaluation Metrics
평가에 사용된 데이터는 LINEMOD, Occluded-LINEMOD, YCB-Video 데이터로 모두 기존 연구들과 동일한 세팅에서 평가를 진행하였으며, 평가 지표로는 6D Pose Estimation에서 일반적으로 사용하는 ADD-0.1d 을 측정하였습니다. ADD-0.1d란, GT pose와 예측 pose를 이용하여 3d 모델을 각자 변환시킨 뒤, 각 point의 거리를 측정하여 3D 모델의 지름에 10% 이하의 오차일 경우 정답으로 보는 평가지표입니다. 또한, BOP challenge에서사용하는 평균 AR도 이용하였다고 합니다.
a. Comparison against SOTA
SOTA self-supervised 6D Pose Estimation 방법론과의 비교를 수행하였으며, LINEMOD와 Occluded-LINEMOD에서 ADD-0.1d를 측정한 결과는 아래의 Table 1,2에서 확인할 수 있습니다.
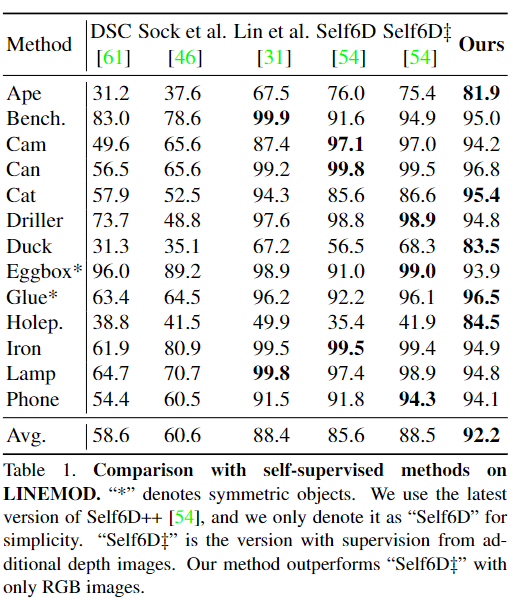
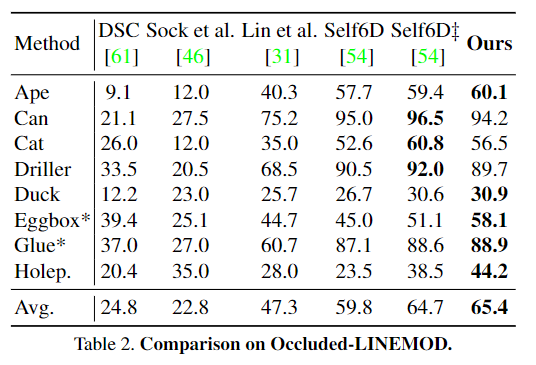
저자들의 방법론의 SOTA 성능을 능가하였으며, 특히 추가적인 depth 정보를 이용하는 Self6D‡에 비해 3.7% 더 높은 성능을 기록하였다는 점에서 더 효과적으로 네트워크 학습이 가능하였음을 이야기합니다. 아래의 [그림 6]는 정성적 결과입니다.

b. Ablation Study
Evaluation of Different componets
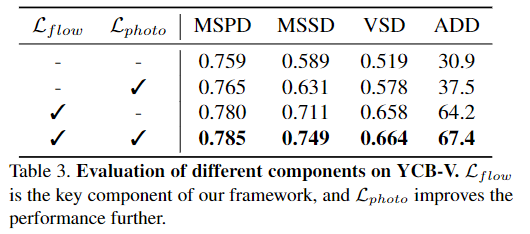
- 1행은 표준적인 teacher-student모델을 의미하며, 2가지 loss를 추가함에 따른 성능 변화를 보였습니다.
- 표준적인 teacher-student 모델의 경우 고품질 pseudo label을 판단하기 어려우므로 성능이 제한적인 결과를 보여주며,
- flow consistency와 phtometric consistency를 고려한 loss를 추가함에 다라 성능이 향상됨을 보였습니다.
Training analysis on YCB-Video
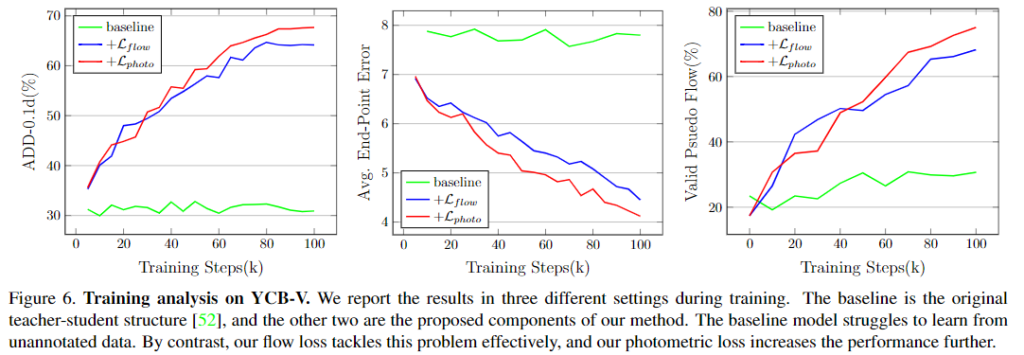
위의 [그림 6]은 pseudo label의 품질을 평가하지 않는 baseline 세팅과 제안된 2개의 loss를 포함할 경우의 성능을 나타낸 그래프입니다. baseline 세팅에서는 pseudo label에 대한 품질을 평가할 수 없어 학습 과정에 큰 어려움을 겪는 것을 확인할 수 있으며, flow loss와 photometric loss를 도입하므로써 모델의 학습 과정에 정제된 pseudo label을 제공하여 성능이 개선됨을 보였습니다.
Evaluation of hyper-parameters
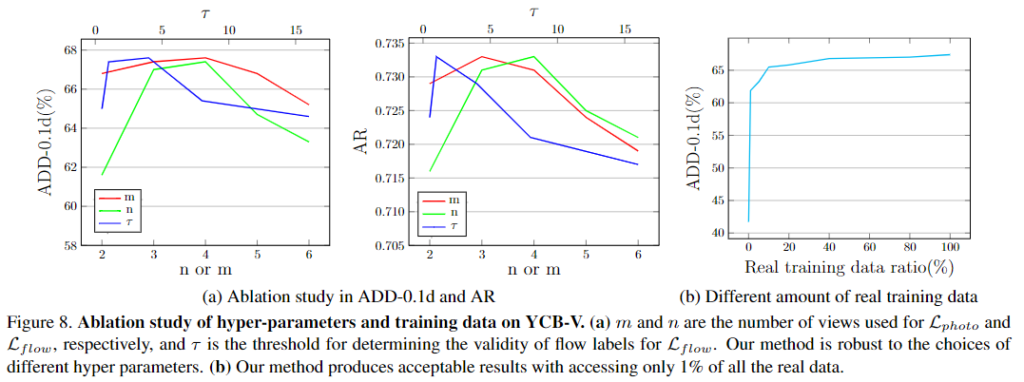
프레임워크의 하이퍼파라미터에 대한 평가로, view가 증가할 수로 성능이 개선되다가 4개 이상의 view를 볼 경우 악영향이 생기는 것을 확인하였습니다. 이에 대하여 저자들은 너무 넓은 view를 볼 경우 겹치는 영역이 적어 네트워크가 학습하기 어려워지는 것으로 분석하였습니다. 또한, 고품질 pseudo label 판단에 사용되는 \tau 에 대한 평가를 수행한 결과 1~4 사이의 값이 잘 작동하는 것을 실험적으로 확인하였습니다.
real data 양에 따른 실험결과는 [그림7]의 (b)에서 확인할 수 있으며, 저자들이 제안한 학습방식은 전체 데이터의 1만을 이용하여 ADD-0.1d에서 약 20.2%정도 성능 개선이 가능함을 확인하였으며, 99%의 실제 데이터를 이용할 경우 성능을 5.5% 더 개선시킬 수 있음을 실험적으로 보였습니다. 이를 통해 저자들의 방식이 데이터가 부족한 경우 효과적으로 작동할 수 있음을 보였습니다.
Evaluation with different initialization and additional annotations
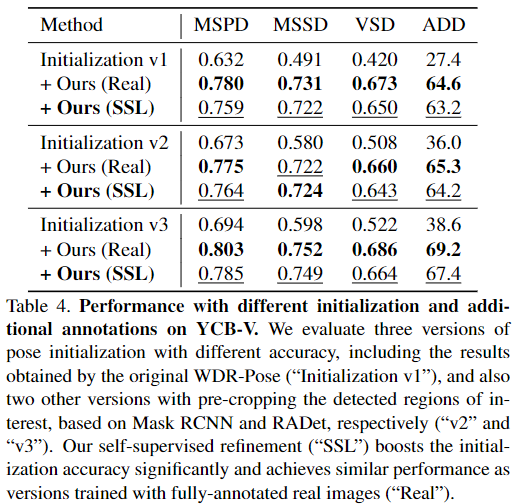
위의 Table 4는 supervised 학습 방식과 3가지의 pose 초기화 방식을 이용하여 실험을 진행한 결과입니다. 해당 실험을 통해 pose 초기화 방식에 따라 성능이 다르지만 대체로 self-supervised 방식으로 학습할 경우 성능이 상당히 개선되며, fully-supervised 방식에 준하는 성능을 달성할 수 있음을 3가지 버전에 대한 Real과 SSL 성능 비교를 통해 확인할 수 있습니다.
Comparison against standard optical flow methods
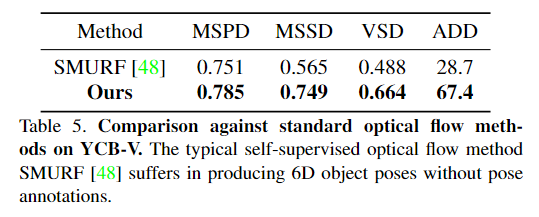
위의 실험은 self-supervised 방식의 optical flow를 통해 렌더링 이미지와 실제 이미지 사이의 2D-to-2D 대응을 직접 구하는 방식과의 비교로, 렌더링 이미지와 실제 이미지 사이의 flow consistency를 구하는 저자들의 방법론과는 다르게 렌더링 이미지와 실제 이미지 사이의 photometric consistency를 이용할 경우 잘 작동하지 않는다는 것을 실험적으로 보였습니다. 저자들은 이에 대해 real 이미지와 합성 데이터 사이의 도메인 gap이 존재하기 때문이라고 분석하였습니다.
Conclusion
해당 논문은 self-supervised 기반의 6D Pose Estimation 방법론을 제안하였습니다. 합성 데이터로 초기 pose를 학습한 뒤, teacher-student pseudo labeling 프레임워크를 통해 refinement를 수행하였으며, 이때 고품질의 pseudo label을 구하기 위해 렌더링 이미지와 실제 이미지 사이의 flow consistency를 구하고, 여러 view의 실제 이미지들 사이의 photometric consistency를 구하여 기하학적 제약을 공식화하였습니다. 저자들이 제안한 방식을 실험적으로 보였으며, 제안된 방법론은 추가적인 depth 이미지나 2D annotation 정보가 필요하지 않다는 점에서 효율적인 학습 방식입니다.
해당 논문은 저자들의 주장을 뒷받침할 수 있는 다양한 실험이 있다는 점에서 설득력있는 것 같습니다. 또한, 고품질의 pseudo label을 어떻게 판단할 지에 대한 고민이 들어있어 해당 기준을 flow 기반의 6D Pose Estimation이 아닌 다른 6D Pose Estimation 방법론에 가져갈 경우에 도움이 될 수 있을 것 같습니다.