안녕하세요 오늘의 X-Review는 ResNet입니다. ResNet은 2015년도 ImageNet Classification 대회인 ILSVRC 대회에서 1등을 차지하고 현재까지 backbone모델로 많이 사용되는 모델입니다. 다들 익숙하신 내용이겠지만 CNN과 VGG모델을 알고 있다는 가정하에 ResNet을 처음 접하시는 분들도 ResNet이 어떤 철학으로 고안되었고 8년이나 지난 지금도 여전히 활용되고 있는 이유에 대해 논문의 내용과 제 설명을 덧붙여 자세하게 리뷰하겠습니다.
Introduction
Deep convolution neural network는 image classification task에서 획기적인 발전을 이뤄냈습니다. 최근의 모델들을 여러 task에서 모델의 깊이가 깊어질 수록(16 ~ 30 layer) 좋은 결과를 낸다는 것을 밝혀줬지만, 모델의 깊이가 깊어질 수록 모델의 수렴을 방해하는 gradient vanishing문제가 생깁니다. 기존의 연구들은 이 문제를 normalized initialization, normalized layers등을 사용하며 10~30 layer의 네트워크를 수렴하게 할 수 있었지만, 그보다 더 깊은 네트워크에서 수렴하기 시작하면 degradation 문제가 생겨 수렴에 어려움이 생깁니다: 네트워크의 깊이가 깊어짐에 따라 정확도가 어느순간 급격하게 저하된는 현상. 이러한 degradation 문제는 ovefitting으로 인한 문제가 아닙니다. 밑의 Figure 1.에서 알 수 있듯, training error는 적지만, test error가 커지는 양상의 oveffing과는 달리 training error, test error 모두 층이 더 적을 때보다 커지기 때문입니다.
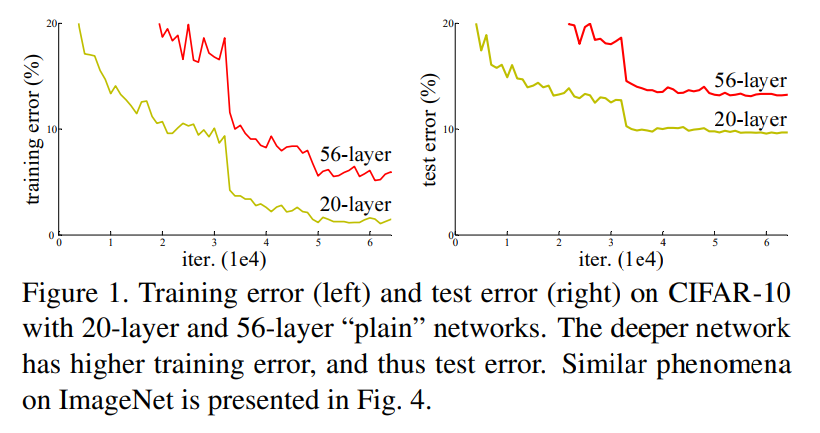
degradation 문제는 모델이 최적화하기 어렵다는 것을 의미합니다. 이에 대한 해결책으로 저자는 identity mapping을 제시합니다. Identity mapping은 convolution을 거치지 않는 얕은 모델에서의 layer를 뒷단으로 그대로 전달하는 것을 의미합니다. 이러한 identity mapping을 쌓는다면 깊은 모델에서도 얕은 모델의 성능을 그대로 따라갈 것이라고 말함과 동시에 쌓여있는 layer가 underlying mapping(기존의 mapping 방식)을 하는 것보다 residual mapping을 하는 것이 더 쉬울 것이라 말합니다.
수식적으로 기존의 underlying mapping을 H(x)라고 할때, F(x) = H(x) – x. 즉, 기존의 매빙 방식인 H(x)가 레즈넷에서는 F(x) + x가 됩니다. 이는 identity mapping이 optimal(x -> x)할때, x가 layer를 거치며 H(x)를 x로 근사시키는 것보다 F(x)를 0으로 근사시키는 것이 더 쉬울것이라는 가정에 기반한 것으로 ‘기존의 input대비 달라지는 정도(resudual)’를 학습시키는 것을 의미합니다.
Deep Residual Learning
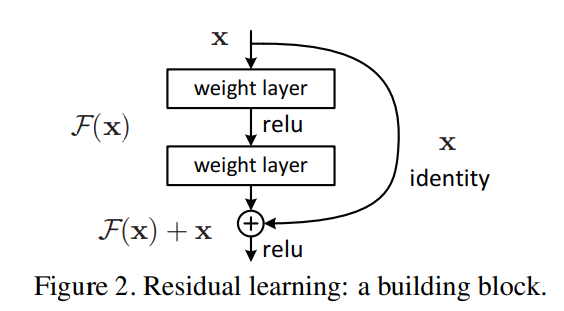
위의 Figure 2. 가 Residual learning의 핵심으로 이전 layer의 출력에서 다음 layer의 출력의 차이만 학습하는 것으로 연산이 간단해지고 error값의 관점에서 학습이 더 쉬워진다고 주장합니다. 이러한 shortcut(x를 그대로 뒤의 layer에 전달하는 것)은 추가적인 parameter혹은 연산 복잡성을 늘리지 않으면서도 모델의 수렴을 돕습니다.
위의 Residual Block(Figure 2.)은 두가지 방법으로 실제 코드에서 구현합니다.
(1) Identity Mapping: y = F(x, Wi) + x
여기서 x와 y는 layer에서 고려하는 input 벡터와 output 벡터이고 +는 element-wise addition을 의미하고 덧셈 이후에 활성화 함수를 거쳐 비선형성을 추가합니다. (1)식은 Identity Mapping으로 input과 output의 차원이 같아야 사용할 수 있으며 추가적인 parameter혹은 복잡성을 요구하지 않습니다. 그렇기에 plain network(기존의 네트워크)와 residual network를 공평하게 비교할 수 있습니다.
(2) Projection Mapping: y = F(x, Wi) + Wsx
(2)식은 Projection Mapping으로 input과 output의 차원이 다를때, input과 output의 차원을 맞춰주기 위해 x에 linear연산을 더해 차원을 맞춰주는 과정을 거칩니다.
Residual Block은 하나의 layer를 통과할때 적용할 수도 있고, 여러개의 layer를 통과할때도 적용할 수 있습니다. 하지만 하나의 layer을 통과할 때 적용하는 것은 linear연산 y = W1x + x을 적용하는 것과 큰 차이가 없기에 2~3개의 layer를 통과할때 적용하게 됩니다.
Network Architecture
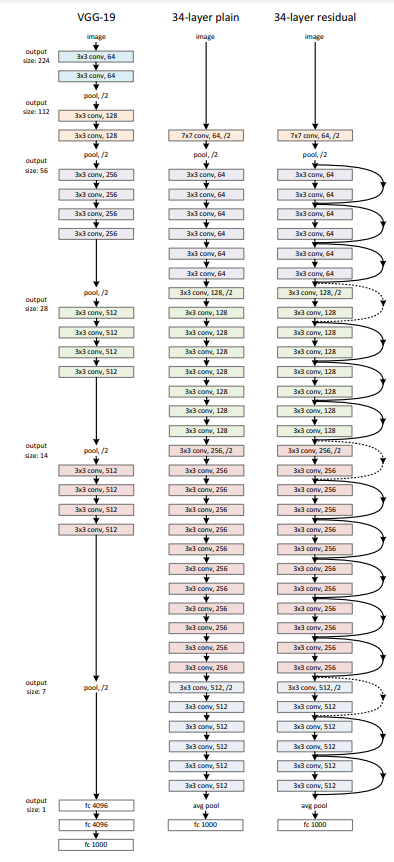

Plain Network
Figure 3.의 가운데에 해당하는 Plain Network즉, Baseline은 VGG의 철학을 빌려 설정되었고, 대부분의 convolution layer들은 3×3 필터로 구성되었으며 다음의 두가지 규칙을 따릅니다.
- 같은 output feature map size에서는 같은 개수의 filter를 갖고 있다.
- feature map size가 절반이 되면 필터의 개수는 두배로 설정한다(layer별 time complexity를 위해).
downsampling은 stride=2의 convolution layer를 거쳐 downsampling되고 마지막은 global average pooling, fully-connected layer를 거쳐 마무리 됩니다. 총 layer는 32개입니다. Baseline의 시간복잡도는 3.6billion FLOPS(컴퓨터의 성능을 수치로 나타낼 때 주로 사용되는 단위)로 19.6billion의 VGG19의 18%정도밖에 되지않습니다.
Residual Network
위의 Baseline을 기준으로 저자는 shortcut connection을 추가했습니다(Fig.3의 우측). identity shortcut ((1)번 수식)은 input과 output의 차원이 똑같을 때(Fig.3 실선) 사용했고 차원이 증가할 때(Fig.3 점선)는 두가지 옵션을 고려했습니다.
(A) shortcut이 identity mapping일때, extra zero entries padding으로 늘어난 차원에 대응했고 추가되는 parameter수는 없습니다.
(B) projection shortcut ((2)번 수식)은 차원을 맞추기 위해 사용되었습니다(1×1 convolution 진행).
두가지 옵션 모두 shortcut들이 피쳐맵을 지나갈 때 stride를 2로 사용했다.
Implementation
이미지를 resize하고 random crop, horizontal flip의 augmentation을 거쳤으며, weight initialization, batch normalization을 사용했습니다. 256 batch size에 SGD optimizer를 사용했으며, learning rate는 0.1로 시작해 error plateaus(error 변화가 적을 때)마다 10으로 나누어주었으며 60*104 iteration 만큼 훈련했습니다. weight decay를 0.0001, momentum을 0.9로 사용했고 dropout은 사용하지 않았습니다.
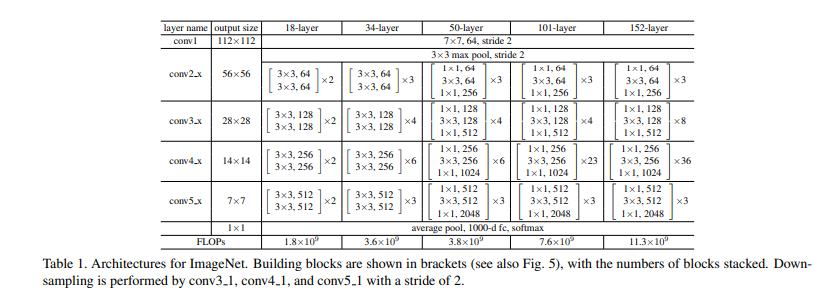
Table 1.은 깊이가 다른 ResNet의 구조를 나타낸 표입니다.
Experients
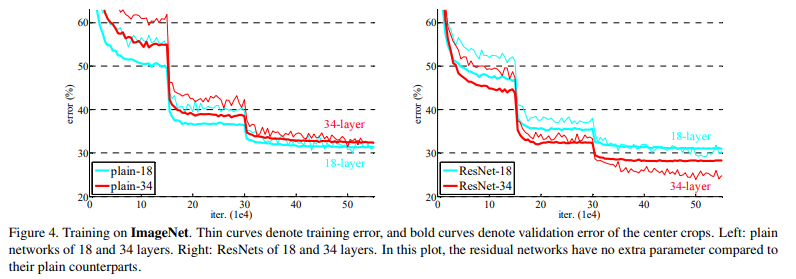
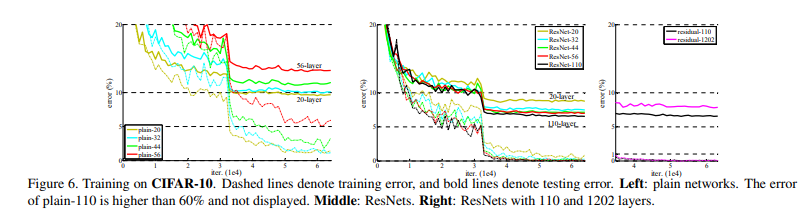
Fig.4의 왼쪽를 확인하면 degradation문제를 볼 수 있습니다. 34-layer모델의 오류가 더 큰 것을 확인할 수 있습니다. 이러한 문제는 training error가 더 깊은 모델에서 높은 것으로 training error는 더 높지만, test할때 error가 커지는 overfitting의 문제는 아닐뿐더러 gradient vanishing문제와는 관련이 없습니다. plain network에서 BN을 적용했고, 저자가 확인해 보았을때 forward, backward 모두 gradient vanishing은 없었기 때문입니다. 반면 오른쪽의 ResNet에서는 더 깊은 모델의 training error가 더 낮게 나오는 것을 볼 수 있습니다.
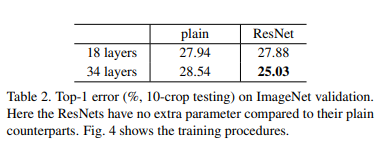
Table 2.는 plain에서 나타나는 error와 resnet에서 나타나는 error를 확인할 수 있습니다. resnet을 적용하는 것은 깊은 모델에서의 학습의 수렴을 도와주려고 고안된 만큼 상대적으로 얕은 모델에서는 plain과 성능이 비슷한 것을 확인할 수 있습니다. 하지만, 학습의 초기단계에서 더 빠르게 수렴하는 것을 Figure 4.에서 확인할 수 있습니다.
Identity vs Projection Shortcuts
parameter-free, identity shortcuts은 학습에 도움이 된다는 것을 확인했습니다. 그리고 저자는 projection shortcuts에 대해 조사했습니다((2)번 수식). Table.3는 3가지(A, B, C)를 비교한 표입니다. .
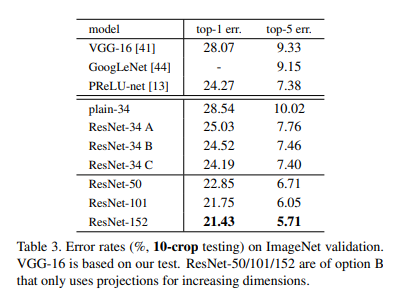
A: zero-padding shortcuts이 차원을 늘리기 위해 사용되었습니다. 그리고 모든 shortcuts들은 parameter-free하다는 특징을 가집니다. (Table.2, Fig.4의 우측과 같은 방식)
B: projection shortcuts이 차원을 늘리기 위해 사용되었고., 다른 shortcuts들은 identity shortcuts입니다.
C: 모든 shortcuts들이 projection shortcut으로 구성된 모델입다.
C > B > A 순서로 성능이 좋았습니다. 저자는 C로 갈수록 파라미터가 늘어나고 성능에 큰 차이가 없어 degradation 문제를 해결하는 데에 projection shortcuts을 차원이 같을 때에도 사용할 필요성을 느끼진 못했다고 평가합니다.
Deeper Bottleneck Architecture
저자들은 기존의 residual block에서 더 나아가 bottleneck block을 고안했고 이는 기존의 residual block에서 차원이 늘어나면서 생기는 bottleneck 문제를 해결하기 위해 고안되었습니다.
병목현상이란 연산해야할게 많아서 말그대로 막히는 현상입니다. 도로가 4차선에서 2차선으로 바뀌게 될때 지나가는 차의 숫자는 그대로인데 통로가 좁아지며 정체현상이 일어나는 현상을 생각해보면 이해하기가 쉬울겁니다: 연산속도가 연산량을 못따라가는 현상을 뜻합니다.
ResNet은 downsampling을 하면서 time complexity의 보존을 위해 채널 수를 2배로 늘려줍니다(ex. 56×56 64채널 → 28×28 128채널).
위 특징 덕분에 VGG보다 채널 수가 적고 깊이를 늘리면서 연산 시간을 줄일 수 있었지만 ResNet이 깊어지면서 채널 수가 늘어나고 연산할 파라미터가 많아지면서 bottleneck 현상이 생길 위험에 빠지게 됩니다. 채널 수가 많아져 연산량이 이전 layer에 비해 늘어나기 때문입니다.
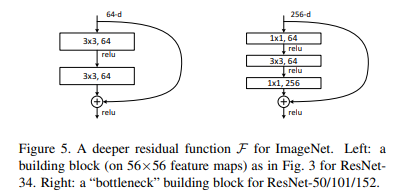
위와 같은 문제를 해결하고자 Figure 5.의 오른쪽과 같은 bottleneck block으로 기존의 block을 대체하여 1×1 convolution을 3×3 앞뒤에 거침으로써 채널 수를 조절합니다(1×1 convolution을 한다는 것은 최소한의 파라미터 및 연산 수로 채널 수를 조절하는 기능을 함).
bottleneck block(오른쪽 블록)을 보면 256채널이 들어오지만 1×1을 거쳐서 64채널로 줄인 후에 3×3 연산을 하고 다시 1×1을 거쳐서 원래의 256채널로 돌려주는 것을 확인할 수 있습니다. 이는 기존 연산대로면 파라미터가 3x3x64x64 + 3x3x64x64 = 73728개로 bottleneck block구조에서는 1x1x256x64 + 3x3x64x64 + 1x1x64x256 = 69632개로 비슷하게 조금 더 적지만 각각의 layer에서의 연산이 분산되어 병목현상이 일어나는 것을 어느정도 완화할 수 있습니다. (PS. 파라미터 개수: 커널의 넓이x커널의 높이x인풋채널의 개수x아웃풋채널의 개수)
저자는 그냥 residual block써도 성능은 비슷하기 때문에 온전히 병목현상을 피하기위한 목적으로 bottleneck block이 사용되었음을 밝힙니다. 간단하게 요약하자면
- ResNet은 연산 속도를 맞추기 위해 피쳐맵 크기를 절반으로 줄일때 채널 수를 두 배로 늘립니다.
- 1의 이유로 모델이 깊어질 수록 채널 수가 늘어나고 한 layer에서의 연산량이 늘어 병목 현상의 위험이 생깁니다.
- 1×1 convolution을 앞뒤로 거치면서 채널 수를 조절하는 것으로 문제 해결했습니다.
이때, bottleneck block은 residual block과 마찬가지로 layer가 늘어나도 학습의 수렴을 돕기에 degradation 문제는 생기지 않습니다.
50-layer ResNet
2-layer block을 3-layer bottelneck block으로 바꿔 34-layer 모델을 50-layer로 늘림.
101-layer and 152-layer ResNet
3-layer block들을 더 사용하여 구성했고 34-layer 보다 성능이 좋아졌습니다.
Comparisons with State-of-the-art Methods
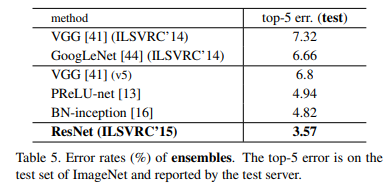
34-layer 모델은 기존의 SOTA모델과 비슷하지만, 152-layer 모델은 단일 모델로도 기존의 SOTA보다 4.49% 좋은 성능을 보였고 6개의 다른 깊이의 모델을 앙상블 하는 것으로 3.57%의 성능을 달성하여 기존의 모델보다 훨씬 더 좋은 성능을 달성함과 동시에 사람의 오차인 5퍼센트보다도 더 좋은 성능을 내 사람을 뛰어넘는 성능을 보입니다.
Further Study
저자는 이에 그치지 않고 CIFAR-10 데이터셋에 대해 152-layer보다도 더 깊은 모델을 구성했을 때에도 잘 수렴하는지 확인하기 위한 실험을 진행합니다.
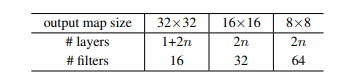
위와 같은 구조로 모델을 구성했으며 구체적인 하이퍼파라미터는 이미지넷에서의 구성과 큰 차이가 없기에 생략하겠습니다.
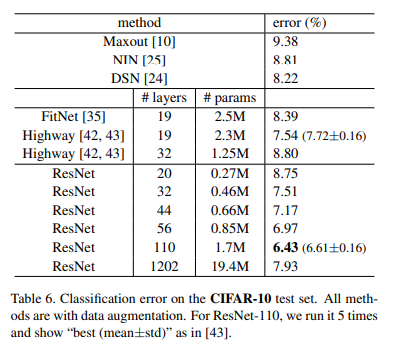
1202-layer에서는 110-layer보다는 낮은 성능을 보이지만 수렴을 잘 한다는 관점에서 엄청 깊은 모델에서도 residual learning이 효과적임을 증명합니다.
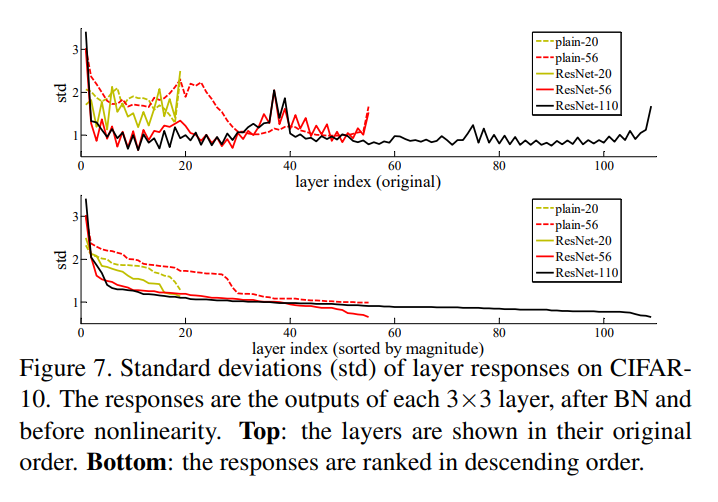
마지막으로 Figure 7.은 CIFAR-10 데이터셋에서 layer response를 나타내는 그래프입니다. Residual Learning은 identity mapping이 깊은 모델에서 학습이 수렴을 하는데 도움을 주는 핵심이라고 생각했고, shortcut을 도입해서 input x를 넘겨주는 것으로 layer마다 변화를 최소화시키는 것으로 degradation문제를 해결하려했습니다. Figure 7.의 그래프는 위의 주장을 증명하고 있습니다.
Plain network는 x -> H(x)로 학습을 하면서 표준편차가 오락가락하는 반면에 residual network는 x -> x + F(x)로 input대비 달라지는 정도만 학습을 하기에 표준편차가 크게 발생하지 않는 것을 확인할 수 있습니다.
ResNet은 기존의 깊은 모델을 쌓는 것이 비선형성을 증가시키고 복잡한 task를 해결하는 데에 도움을 주지만 어느정도 깊이를 넘어서면 오히려 얕은 모델보다 성능이 안좋아지는 degradation 문제를 정의하고 이를 해결한 논문으로 8년이 지난 지금도 backbone으로 활용되고 있습니다. 논문을 보며 residual learning의 강력함을 알 수 있음과 동시에 기존의 방법론의 문제를 정의하는 것이 얼마나 중요한지 다시 알 수 있었습니다.
ResNet의 Identity Mapping에 대해 찾아보며 ResNet의 Identity Mapping을 자세하게 다루는 논문(Identity Mappings in Deep Residual Networks)이 있다는 것을 알게 되었는데 이 논문도 읽어보고 기회가 된다면 리뷰하도록 하겠습니다.
ResNet리뷰는 여기서 마치겠습니다. 그동안 X-Review를 소홀히 하고 있었는데 앞으로는 성실하게 X-Review작성하고, 댓글 달 수 있도록 하겠습니다. 리뷰 읽어주셔서 감사합니다.
안녕하세요. 박성준 연구원님.
좋은 리뷰 감사합니다. 정리가 정말 상세하네요.
몇가지 여쭤보고 싶은 부분이 있습니다.
1. 병목현상은 전체 프로세스에서 처리 가능 대역폭이 제한적인 일부 영역으로 인해 전체 프로그램의 실행 속도가 늦어지는 것으로 단순히 연산의 총량이 늘어나 연산 속도가 느려지는 것과는 거리가 있는데, ResNet 상에서 병목 문제가 발생하는 부분이 있나요?
2. ResNet의 bottleneck구조가 그림 5의 좌측과 같이 해당 구조를 적용하지 않은 신경망에 비해 장점이 연산량의 차이밖에 없나요?
감사합니다!
지오님 좋은 답변 감사합니다.
1. ResNet은 신경망이 깊어지며 downsampling을 거칠때 채널수를 두배로 늘립니다. 3×3커널을 사용하고 input channel=50, output channel=100이라고 가정하면 연산할 파라미터의 개수가 3x3x50x100개가 되게됩니다. 채널수가 늘어날 수록 한층에서의 파라미터 수가 증가하며 실행속도가 느려지게됩니다. 즉, ResNet의 top layer에 가까워질수록 병목현상이 발생합니다.
2. 한번에 처리할 연산량이 줄어듦에 따라 연산속도가 빨라지고, convolution layer를 깊게 쌓아 비선형성이 증가하고 모델의 정확도도 증가하게됩니다. 실제로 같은 구조지만 residual block을 사용한 ResNet34모델보다 bottleneck block을 사용한 ResNet50모델이 성능이 좋습니다.
안녕하세요 성준님, 좋은 리뷰 감사합니다.
아직 전부 자세히 이해한것은 아니지만, 하나씩 이해하는 과정에서 먼저 궁금한점 남기겠습니다.
우선 잔차를 학습한다는 개념이 진짜 이해가 안됐었는데 이해를 했습니다. 다만 한 layer를 통과하면 선형연산을 하는것과 거의 차이가 없다고 하셨는데, ReLU 를 거치긴 하니까 1 layer만 통과해서 잔차학습을 진행시키더라도 원하는 성능이 나와야하는게 아닌가 싶습니다. 답변해주시면 감사하겠습니다.