이번에 리뷰한 논문은 quantization 분야의 논문입니다. 그 중에서도 binary neural network 논문을 가져왔는데요, 모델의 가중치가 0혹은 1로 표현된 binary 모델을 학습하여 full precision의 모델과 비슷한 성능을 달성하였다고 합니다.

Introduction

본격적으로 리뷰에 들어가기 앞서 Binary Neural Net(BNN)에 관해 설명드리겠습니다. BNN이란 이름에서 알 수 있듯 가중치가 0혹은 1로 구성된 네트워크를 의미합니다. 우리가 일반적으로 사용하는 FP32(32비트로 하나의 숫자를 표현하는 방식)로 이루어진 모델을 1 비트로 표현하도록 극단적인 quantization을 적용한 모델이라고 이해하시면 됩니다.

논문에서는 이러한 BNN이 한정된 연산 자원을 가진 device에 매우 효율적이라고 주장하며 BNN두 가지 장점을 언급하였습니다.

하나는 모델 압축 능력이 뛰어나다는 것입니다. BNN에 사용되는 binary convolution에는 하나의 가중치 값을 표현할 때 1 비트의 메모리만 사용하기 때문에, 네트워크의 가중치가 32비트로 표현되는 모델에 비해 메모리 사용량이 32배 줄어들게 되겠죠. 이는 half-precision(FP16)이나 int8보다 더 효율적인 메모리 사용이라고 볼 수 있을 것 같습니다.

다른 하나는 연산 속도가 빨라진다는 것입니다. 예를 들어 일반적으로 convolution연산을 수행한다고 했을 때, 부동 소수점으로 표현된 input과 weight간의 곱셈 연산이 진행됩니다. 그러나 BNN의 경우 이러한 소수점 연산이 xnor및 pop-count 연산으로 대체되어 보다 빠르게 연산을 수행할 수 있습니다.

이러한 hardware친화적인 장점들이 존재함에도 불구하고, BNN은 실제 시나리오에서는 거의 사용되지 않았다고 하는데요, 그 이유는 binary로 quantize했을 때 real-value(full-precision)네트워크에 비해 정확도가 크게 떨어지기 때문이라고 합니다.

논문의 저자들은 real-value 네트워크에 버금가는 BNN을 설계하고자 하였는데요, 이를 위해 기존 방법론들을 통합하여 하나의 강력한 baseline을 설정하고, binary convolution과 real-value convolution 출력값 간의 차이를 최소화하도록 하는 두 가지의 모듈을 제안하였습니다.

먼저, 저자들은 attention matching을 사용하여 optimization 과정에서 real-value 네트워크가 binary 네트워크를 더 밀접하게 guide 할 수 있도록 하였습니다. 좀 더 단순히 표현하자면 BNN real 네트워크를 학습할 때 real 네트워크를 teacher로 활용하였다는 것이라고 이해하시면 될 것 같은데요, 그러나 BNN의 구조적 차이로 인해 teacher-student 방식을 직접 적용하는 것은 최적의 성능을 내지 못하였기 때문에, 점진적으로 구조적 간극을 좁히도록 하는 sequence of teacher-student pairs를 사용할 것을 제안하였습니다.

다음으로는 binary convolution 이전에 이루어지는 binarization에 앞서 얻을 수 있는 실수 값 활성화를 사용하여 scale factor를 계산하고, 이를 이용하여 binary convolution 적용 후 활성화를 재조정하는 방법을 추가로 제안하였습니다. 이는 최근 연구에서 binary convolution의 출력을 재조정함으로써 큰 성능 향상을 이룬 것과 비슷한 방식인데요, 이전 연구들과는 달리, 본 논문에서는 binarization에 앞서 각 레이어의 real-value activation을 기반으로 한 data-driven 방식으로 scaling factor를 계산하여 더 우수한 성능을 달성하였습니다.

아래 [그림 1]이 저자들이 제안하는 real-to-binary block과 data-driven channel re-scaling입니다.

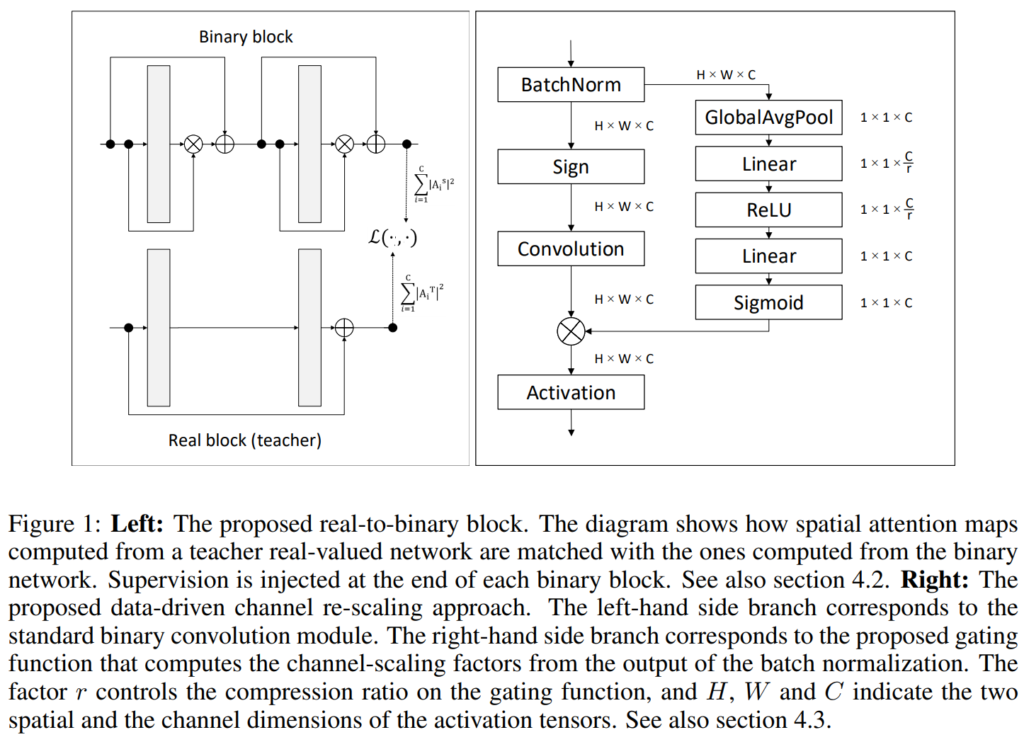
본 논문의 contribution은 다음과 같습니다.

• We construct a very strong baseline by combining some recent insights on training binary networks and by performing a thorough experimentation to find the most well-suited optimization techniques. We show that this baseline already achieves state-of-the-art accuracy on ImageNet, surpassing all previously published works on binary networks.
• We propose a real-to-binary attention matching: this entails that matching spatial attention maps computed at the output of the binary and real-valued convolutions is particularly suited for training binary neural networks. We also devise an approach in which the architectural gap between real and binary networks is progressively bridged through a sequence of teacher-student pairs.
• We propose a data-driven channel re-scaling: this entails using the real-valued activations of the binary network prior to their binarization to compute the scale factors used to re-scale the activations produced right after the application of the binary convolution.
• We show that our combined contributions provide, for the first time, competitive results on two standard datasets, achieving 76.2% top-1 performance on CIFAR-100 and 65.4% top-1 performance on ImageNet when using a ResNet-18 –a gap bellow 3% and 5% respectively compared to their full precision counterparts.

Background

논문에서 제안하는 baseline이 (Courbariaux et al., 2016)에서 제안된 BNN의 binarization process를 기반으로 하고 있기 때문에 해당 방법론에 대해 먼저 설명드리고 넘어가도록 하겠습니다.

Conv 레이어의 가중치와 input feature가 각각 W \in \mathbb{R}^{o \times c \times k \times k} 와 A \in \mathbb{R}^{c \times w_{\text{in}} \times h_{\text{in}}}라고 가정해 보겠습니다. 여기서 o와 c는 각각 출력과 입력 feature의 채널 수를, k는 kernel의 크기를 나타내며, w_{\text{in}}과 h_{\text{in}}은 input feature A의 spatial dimension을 나타냅니다. ((Courbariaux et al., 2016))에서는 가중치와 activation map 모두 sign 함수를 사용하여 이진화한 후, A \ast W \approx \text{sign}(A) \circledast \text{sign}(W)로 convolution을 수행하는데, 여기서 \circledast는 binary convolution을 의미합니다.

그러나 이러한 직접적인 binarization은 높은 binarization error가 발생하며, 결과적으로는 모델의 정확도가 낮아지는데요, 이를 완화하기 위해 (Rastegari et al., 2016)의 XNOR-Net에서는 real-value의 scaling factor를 사용하여 binary convolution의 출력값을 아래와 같이 재조정하였다고 합니다.

위의 [수식 1]에서 \odot는 element-wise multiplication을 나타내며, \alpha와 K는 각각 가중치와 activation scaling factor를 나타내고 있습니다. 더 최근에 Bulat & Tzimiropoulos (2019)는 \alpha와 K를 단일 factor \Gamma로 통합하여 backpropagation을 통해 학습하자고 제안하였고, 이를 통해 정확도를 크게 항상시켰다고 합니다.

Method

Building a strong baseline

가장 먼저 저자들을 기존의 binary quantization의 baseline을 설정하는 것 부터 시작하였습니다. 당시 거의 모든 binary network 연구에서 XNOR-Net과 BNN을 baseline model로 사용하였는데요, 저자들은 이에 더해 다른 연구에서 논의되었던 통찰과 표준적인 optimization을 통합하여 새로운 baseline을 설정하여 sota를 달성하였다고 합니다. 사실상 다른 논문에서 진행되었던 hyperparameter tuning 결과를 붙인 것으로 보입니다.

최종 baseline은 resnet-18을 기반으로 아래와 같은 방법들을 적용하였다고 하네요.

model architecture

• Block structure: XNOR-Net의 modifed ResNet구조를 사용하였습니다. BatchNorm → Binarization → BinaryConv → Activation 순으로 연산이 진행되며, skip connection을 블록의 마지막에 진행한다고 하네요. Activation을 binarize 하기 위해 sign 함수를 사용하는데요, 0은 양수로 취급하였습니다.
• Residual learning: (Liu et al., 2018)에서 제안된 double skip connection을 사용하였습니다.
• Activation: PReLU를 사용하였습니다. (Bulat et al., 2019)에서 PReLU가 binary network의 training을 촉진한다는 것을 보였기 때문에 사용하였다고 하네요.

Training method

• Initialization: binary network를 학습할 때, 2단계로 optimization을 진행한다고 합니다. 먼저 binary activation과 real-value weight를 사용하여 학습한 다음, 학습된 모델을 초기값으로 사용하여 weight와 activation이 모두 binary인 모델을 학습한다고 합니다.

이밖에도 weight decay, data augmentation optimize scheduler 등을 사용하였는데요, 다른 논문에서 사용된 기법들을 사용하였습니다. 구체적인 hyperparameter값은 논문을 참고하시면 좋을 것 같네요.

Real-to-binary attention matching

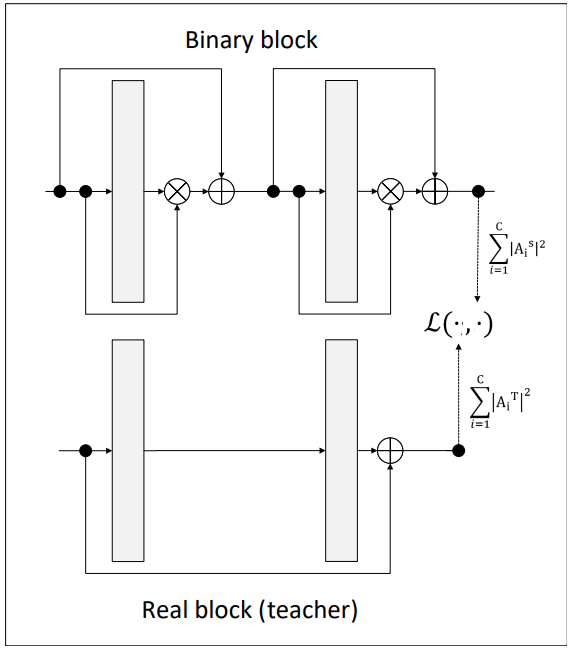
Baseline을 설정하였다면 이제 이를 개선시킬 방법론을 소개하는 일이 남았는데요, 저자들은 binary network와 real-value network간의 성능 차를 줄이기 위한 방법으로 binary network와 real-value network에서 추출한 attention map을 매칭시키는 손실 함수를 제안하였습니댜. 이를 위해 저자들은 한 가지 가설을 세웠는데요, 저자들은 어떤 real-value의 convolution network를 binarize한다고 할 때, Binary network의 binary convolution 레이어의 출력값이 그에 대응되는 real-value convolution 레이어의 출력값과 비슷해지도록 하면 binary network의 성능 드랍이 줄어들 것이라고 생각하였습니다. 이에 위의 그림과 같이 teacher와 student학습 방식을 응용하여 각 convolution 블록의 마지막 부분에서 binary와 real-value의 activation map을 비교함으로써 binary의 학습에 제약을 가하는 Loss를 제안하였습니다.

네트워크 내의 일련의 전달 지점들인 𝒥 집합에서 attention-matching 매칭을 적용한다고 할 때, 전체 Loss는 아래의 [수식 2]와 같이 표현될 수 있습니다.

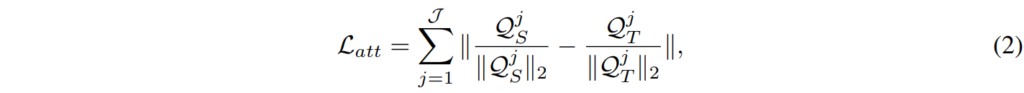
여기서 Q^j는 input feature A의 i번째 채널인 A _i의 activation map을 의미합니다.

progressive teacher-student

저자들은 teacher와 student가 가능한 한 유사한 구조를 갖는 것이 중요하다는 것을 관찰했다고 하며, real network와 binary network 간의 차이를 점진적으로 연결하도록 학습하였습니다. 단계별로 나타내면 아래의 세 단계를 거친다고 하네요.

1. teacher는 standard ResNet 구조의 real-value network이며, student는 마찬가지로 real-value network이지만 binary ResNet-18과 같은 구조로 설계합니다.(위의 baseline에 나온 기법들을 적용하여 디자인하였다고 하네요) 여기서는 binary ResNet-18의 activation function에 실제 binarization 함수(sign) 대신 continuous한 activation 함수(Tanh 함수)가 사용되었습니다. 이러한 방식으로 학습하여 네트워크 자체는 여전히 real-value로 구성되어 있지만 standard보다는 binary resnet과 더 유사하게 동작하게 됩니다.
2. step 1에서 얻은 network를 teacher로 사용하고, student는 binary activation, real-value weight 모델을 사용
3. step 2에서 얻은 network를 teacher로, binary weight, binary activation을 student로 사용합니다.

정리하자면 standard model(real activation, real weight) -> binary model(real activation, real weight) -> binary model(binary activation, real weight) -> binary model(binary activation, binary weight) 순으로 점진적인 변화를 주면서 학습을 진행하였습니다.

Data-driven channel re-scaling

앞서 소개한 real-to-binary attention matching을 통해 binary network의 optimization을 개선시킬 수는 있지만, 여진히 binary convolution은 제한적인 표현력을 가지고 있으며, 이로 인해 real-value network를 근사하는 능력이 떨어진다고 합니다. 따라서 real-value input을 고려하여 scaling factor를 조절하는 data-driven channel re-scaling을 도입하여 binary network의 표현 능력을 높이면서도 연산량이 크게 증가하지 않도록 하였습니다.

기존 연구들은 실제 convolution을 더 잘 근사하기 위한 목적으로 binary convolution의 re-scaling의 효과성을 보여주었습니다. XNOR-Net(Rastegari et al., 2016)은 이러한 scaling factor를 분석적으로 계산하는 방법을 제안했고, (Bulat & Tzimiropoulos, 2019; Xu & Cheung, 2019)은 학습을 통해 학습하는 방법을 제안했는데, 이는 추가적인 정확도 향상을 보여주었다고 합니다. 후자의 경우, 학 중에는 average expected loss을 최소화하는 fixed scaling factor를 찾는 것을 목표로 최적화가 진행된다고 하네요. 저자들은 이를 넘어서 구별적으로 훈련된 input-dependent scaling factors를 얻는 방법을 제안하였습니다. 즉, scaling factor가 inference 시 입력되는 데이터에 의해 유동적으로 변하게 되는 것이죠.

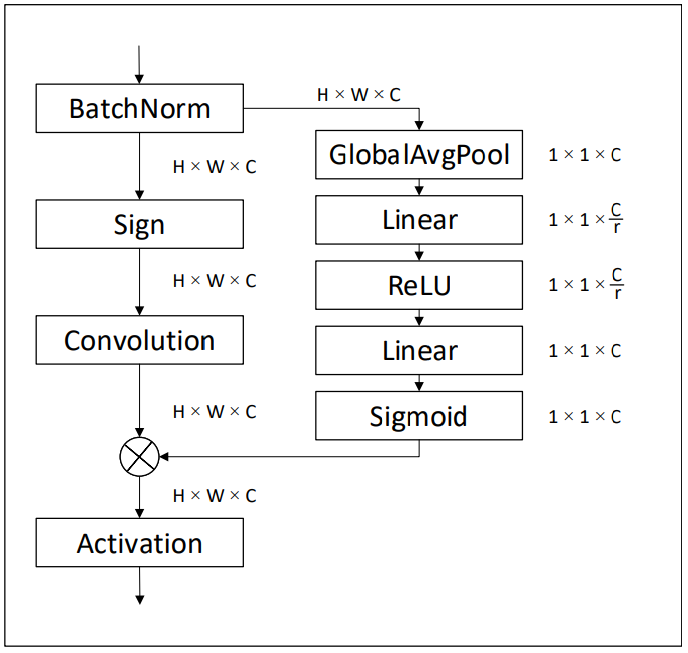
먼저 binary block을 통과하는 흐름을 정리하자면 위의 그림과 같습니다. 위 그림의 왼쪽 부분이 binary block을 나타내고 있는데요, 여기에 입력되는 값들을 real-value입니다. input image(activation)에 batch normalization을 적용하고, 그 출력값을 binarization하면 sign 함수에 의해 값의 표현 범위가 변화하여 정보의 손실이 발생하겠죠. 이어서 binary convolution, re-scaling 및 PReLU가 수행됩니다.

저자들은 binarize로 인해 발생하는 큰 정보 손실 이전에, 사용 가능한 full-precision activation을 사용하여, binary convolution의 출력을 channel-wise로 re-scale하기 위해 사용되는 스케일 인자들을 예측하는 것을 제안하였습니다. 구체적으로, convolution의 근사화는 아래의 [수식4]와 같습니다.

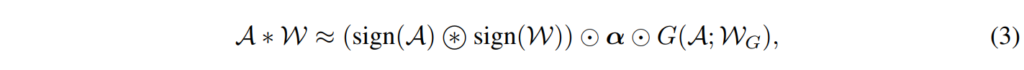
여기서 W_G 는 gating function G 의 파라미터입니다. 이 함수는 binary convolution의 출력값을 re-scaling하기 위해 사용되는 scale factor를 계산하며, real-value의 activation을 입력으로 사용합니다. 바로 위에 있는 그림은 저자들이 구현한 G 함수입니다.

Computational cost analysis

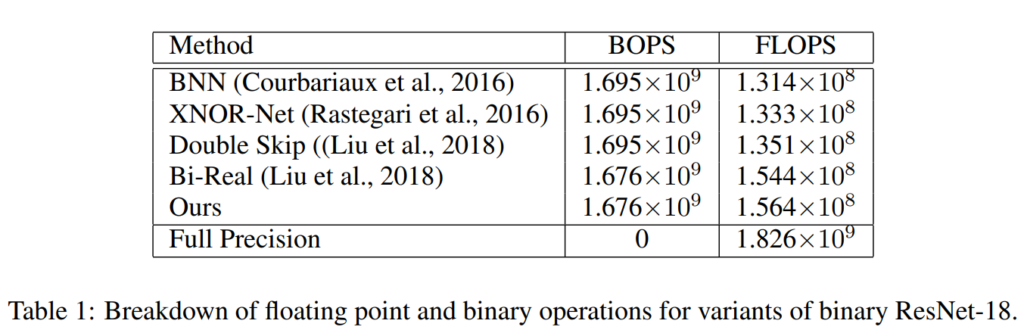
[표 1]은 다양한 binary 네트워크 방법론들의 연산량을 나타내고 있는데요, 여기서는 binary 연산(BOPS)와 부동 소수점 연산(FLOPS)를 구분하여 리포팅하였습니다.

저자들이 보여주고 싶었던 것은 동일 BOPS에서 FLOPS의 차이인데요, data-driven channel re-scaling으로 인해 저자들이 제안한 방법론에서는 기존 방법론들보다 부동 소수점 연산이 증가하였는데요, 그러나 이는 미비한 수준으로 [표 1]에 따르면 동일한 binary연산의 연산량이 동일할 때 약 1%의 FLOPS만이 증가하였음을 강조하였습니다.

Results

실험은 ImageNet과 CIFAR-100데이터셋을 사용하였는데요, ImageNet으로는 sota 방법론과의 비교를 수행하였고, CIFAR-100으로는 ablation study를 수행하였다고 합니다.

Comparison with the SOTA

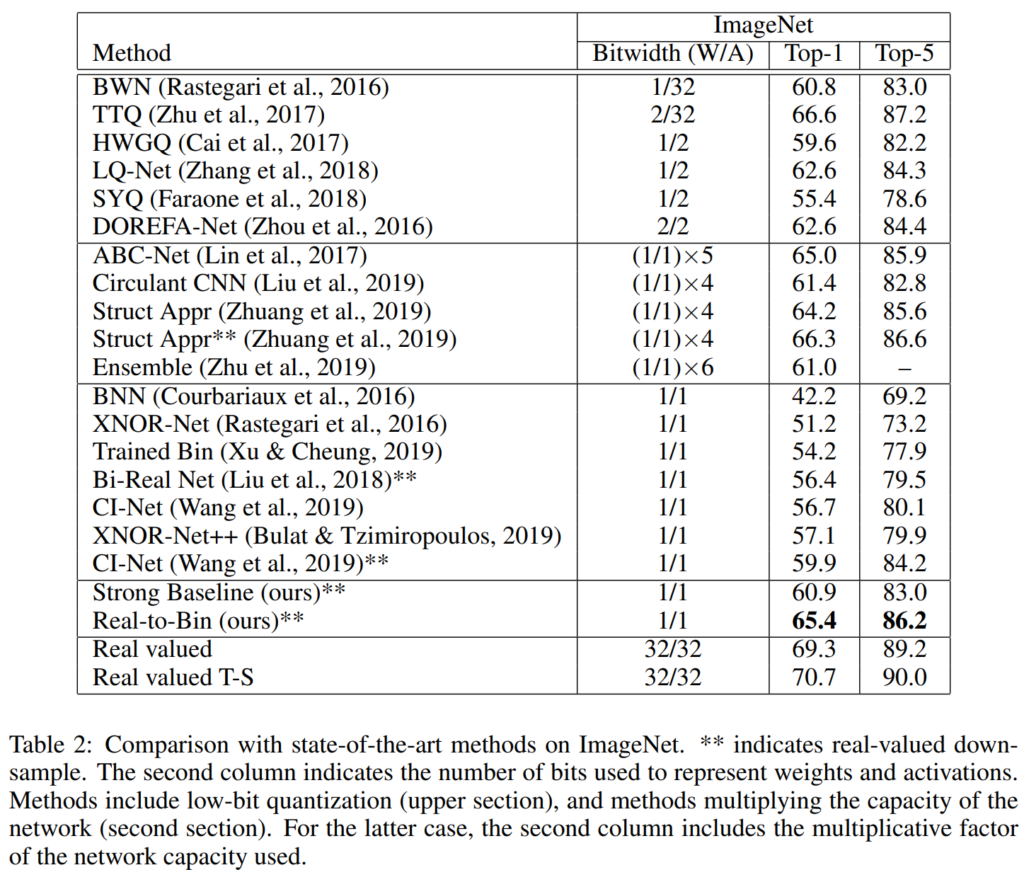
[표 2]는 binary이외에도 low-bit quantization 방법론들과 저자들이 제안한 방법론을 비교한 결과를 나타내고 있습니다.

다른 binary network와 비교하였을 때, 저자들의 baseline이 이미 기존 sota인 CI-Net보다 약 1% 높은 성능을 보인 것을 확인할 수 있습니다. 여기에 저자들이 제안하는 Real-to-Bin 모델이 baseline에 비해 top-1 accuracy가 5.5%가량 증가하여 binary quantization의 sota를 달성하였다고 하네요.

Real-value network와 비교하면 저자들의 제안한 binary 모델은 대응되는 모델과의 성능 차이를 ∼4% 정도로 줄였으며, attention transfer로 학습된 real-value network와 비교했을 때도 ∼5% 정도의 차이로 준수한 성능을 보인다고 합니다.

다른 low-bit quantization 방법론들과 비교하였을 때도 저자들의 방법론이 좋은 성능을 보이는 것을 확인할 수 있는데요, TTQ를 제외한 다른 모든 모델보다 좋은 결과를 내는 것을 확인할 수 있습니다.

Ablation studies

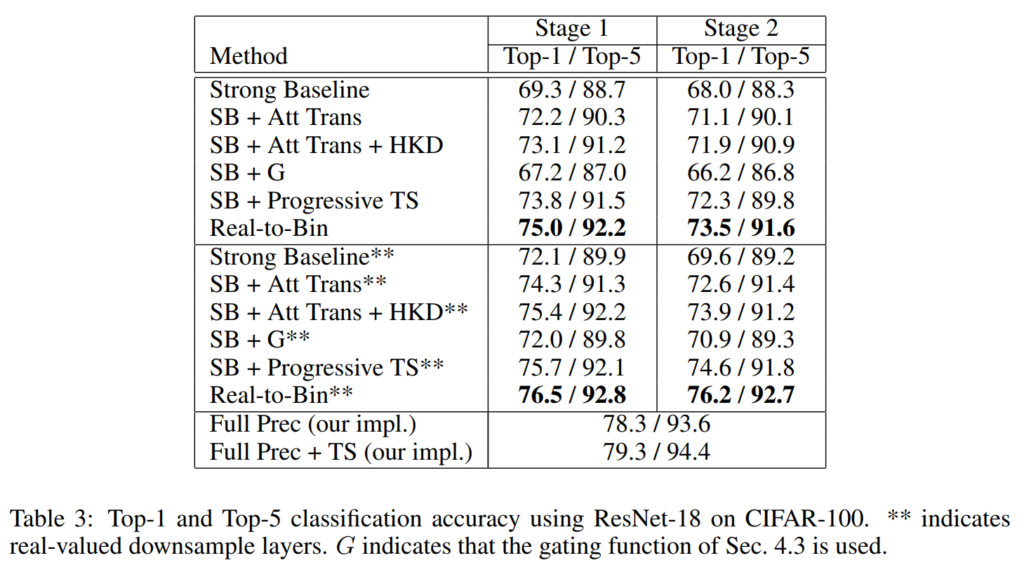
저자들은 CIFAR-100으로 ablation study를 수행하였습니다.

Teacher-Student 효과

ResNet-34를 teacher로 사용하여 실제 값(Real-valued) ResNet-18을 학습시키면, top-1 정확도가 약 1% 향상되는데요, 저자들의 progressive teacher-student 를 통해 학습한 경우, top-1 acc가 약 5% 향상되는 것을 볼 수 있습니다. 논문에서는 이러한 결과를 통해 progressive한 t-s가 binary network를 학습할 때 필수적이라고 주장하였습니다. .

Real-value와의 성능 비교

CIFAR-100에서 full-precision ResNet-18과 비교할 때, 저자들의 Real-to-Bin이 real-value 네트워크와의 격차를 약 2%로 줄였으며, teacher supervision을 사용하면 약 3%로 줄인 것을 확인할 수 있습니다.

Binary vs Real-valued downsample

저자들이 제안한 방법은 binary downsample layer나 real-value downsample layer를 사용하였을 때 유사한 성능 향상을 달성하였으며, top-1 acc가 각각 약 5.5%와 6.6% 상승하였습니다. 또한, ablation study에 대한 결과가 모든 항목에 대해 두 경우 모두에서 일관성이 존재하네요.

Scaling factor와 attention matching

논문에서 주목한 점은 attention matching이 없을 때 gating 모듈이 효과적이지 않다는 것입니다(SB+G). 이 결과로 인해 두 요소가 상호 연결되어 있다는 것을 증명하였다고 합니다.