안녕하세요. 제가 처음으로 쓰는 X-Review의 주제는 딥러닝의 기초입니다. 기초 교육을 받으며 공부한 내용을 정리하여 작성하겠습니다.
신경망이란
인간은 뉴런이라고 하는 인간의 뇌세포로 복잡하게 연결된 네트워크를 형성하고, 뉴런들이 보내는 전기 신호로 정보들을 처리합니다. 신경망(Neural Network)은 인간의 두뇌가 작동하는 방식에서 영감을 받아 노드라고 부르는 인공 뉴런들을 활용하여 여러 층(layer)을 만들어 정보를 처리하는 알고리즘입니다.
활성화 함수(Activation Fuction)
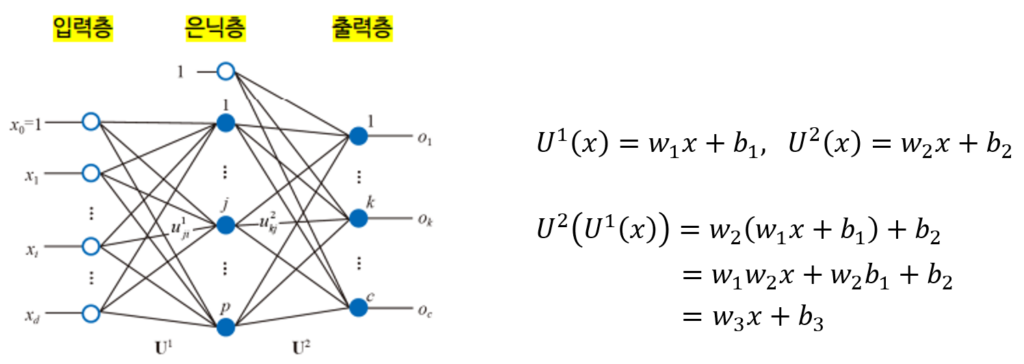
노드가 다른 노드로 연결될 때, 가중치(weight)가 곱해지고 편향(bias)이 더해지는 선형적인 affine연산이 진행됩니다. 이때 활성화 함수를 거치지 않는다면 은닉층을 많이 쌓아도 다른 weight값을 가지는 하나의 층을 거치는 것과 같은 역할을 하기 때문에 선형문제로 해결할 수 없는 문제들을 해결 할 수 없습니다. 따라서 비선형 활성화함수를 거쳐 직선으로 해결할 수 없는 문제를 해결할 수 있도록 비선형성을 더해줍니다.
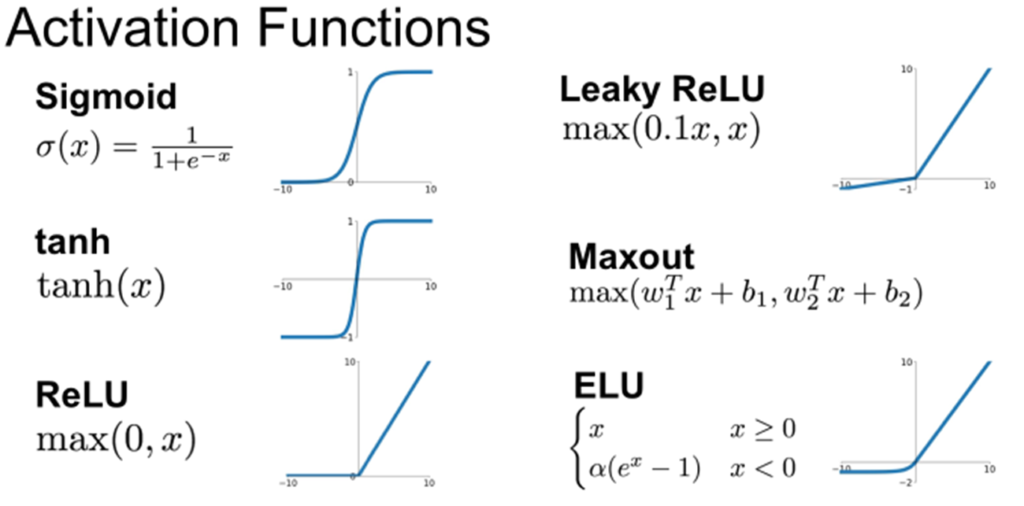
위와 같은 함수들이 비선형성을 더해주는 활성화 함수들의 예시입니다. Sigmoid함수는 0 ~ 1, tanh함수는 -1 ~ 1의 범위로 출력해주는 함수로 비선형성을 더해줍니다. 하지만, 이 두 함수의 기울기 값은 0과 1사이의 값을 갖고, 0으로 부터 멀어질수록 값이 0에 가까워지기 때문에 계층을 많이 거칠수록 여러번 연산되며 기울기가 0으로 수렴해 없어지게 됩니다. 이는 신경망의 학습을 위해 역전파를 거칠때 기울기 0으로 소실되어 가중치가 갱신되지 않는 문제가 생깁니다.
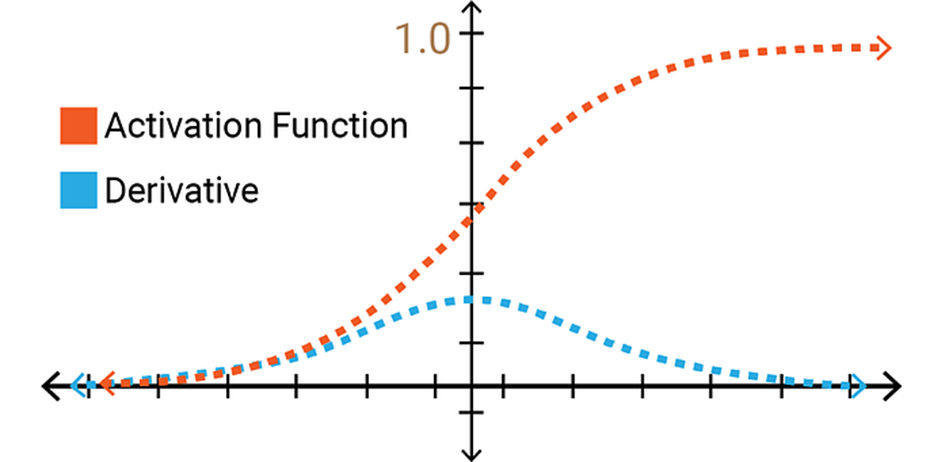
Sigmoid와 tanh함수의 기울기가 소실되는 문제점을 해결하기 위해서 고안된 활성화 함수가 바로 ReLU함수 입니다. ReLU함수는 비교적 간단한 구조로 0보다 작은 범위에서는 0, 0보다 큰 범위에서는 x로 입력값을 그대로 출력합니다. ReLU함수의 기울기 값은 음수일때는 0, 양수일때는 1로 기울기가 소실되는 문제를 어느정도 해결하여 현재 많이 사용되는 활성화 함수 중에 하나 입니다. 하지만 입력값이 음수일때에는 기울기가 0으로 전파가 되지 않는 문제가 있는데 이를 보완하고자 Leaky ReLU와 ELU가 제안되었습니다.
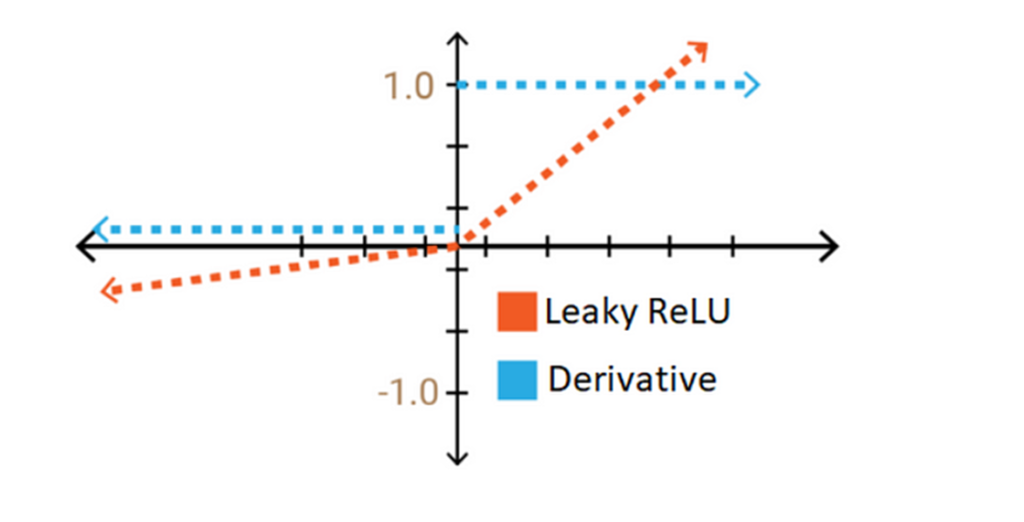
Leaky ReLU와 ELU모두 음수에서의 기울기가 0이 아닌 작은 수를 갖게하여 기울기가 0으로 없어지는 것을 방지하였고 양수, 음수 모든 범위에서 기울기가 없어지는 문제를 해결했습니다.
최적화 기초
경사하강법(Gradient Descent)
경사하강법은 경사를 따라 내려가면서 weight를 업데이트해 Minimum값을 찾는 방법입니다. 경사는 함수의 최대 증가방향 기울기 벡터를 의미합니다. weight의 변화에 따른 cost의 증감을 이용하여 cost가 작아지는 방향으로 학습을 진행합니다. 수식적으론 weight값에 기울기에 learning rate를 곱한 값을 빼는 것으로 weight값을 갱신합니다. 이는 기울기가 감소하는 방향으로 weight를 갱신시키는 것이 cost값을 낮출 수 있기 때문입니다.
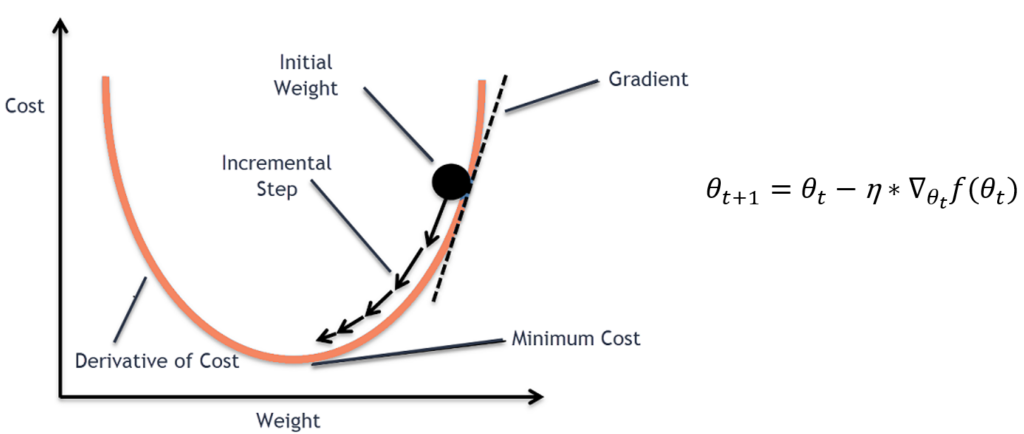
하지만, 이러한 경사하강법은 국소적인 최소점(local minimum)에 빠진다는 단점과 learning rate값에 민감하다는 단점이 있습니다.
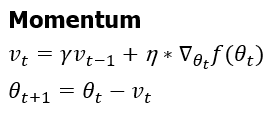
국소적인 최소점(local minimum)에 빠지는 단점을 해결하기 위한 방법으로 고안된 것이 momentum입니다. momentum은 물리에서는 운동량이라는 뜻으로 관성처럼 기존의 momentum(이전 gradient값)과 현재의 gradient값을 모두 고려해서 local minimum에 빠지지않고 지나칠 수 있도록 도와주는 방법입니다. Momentum은 현재 parameter 위치에서 gradient를 계산하고 현재의 모먼트 Vt를 구하여 momentum만큼 업데이트합니다.

learning rate에 민감하다는 단점을 해결하기 위하여 고안된 것이 Adagrad입니다. 고정된 learning rate를 사용하는 것이 아니라 상황에 맞게 learning rate값을 다르게 학습하는 방법입니다. 이전 step에서의 기울기들의 제곱을 모두 합하여 분모에 둠으로써 learning rate값이 처음에는 크게 나중에는 작게하여 학습을 더 효율적으로 할 수 있게 합니다.
하지만, Adagrad의 경우 학습이 진행됨에 따라 Gt값이 너무 커져 나중에는 학습이 거의 되지 않는다는 단점이 있습니다. 이를 해결하기 위해서 Adagrad에 지수가중평균의 개념을 도입한 방법이 RMSprop입니다.
지수 가중 평균(Exponential Weighted Averages)
RMSprop으로 바로 넘어가기 전에 먼저 지수 가중 평균이란 데이터의 이동 평균을 구할때 오래된 데이터가 미치는 영향을 지수적으로 감소하도록 만들어 주는 방법입니다.
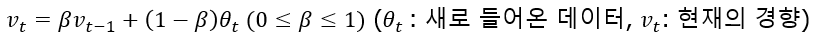
베타값은 과거의 경향성, (1-베타)는 새로운 경향성으로 베타값이 0 ~ 1 사이의 값을 가지므로 제곱할수록 작아지기에 오래된 데이터일수록 현재의 경향을 나타내는 데 적은 영향을 미치게 됩니다. 이는 제곱을 할수록 0에 수렴하기 떄문에 근사적으로 1/(1-베타)일 간의 데이터만을 사용하여 평균을 내는 것과 같은 역할을 합니다.
예를 들어 베타값이 0.9라고 한다면 과거의 경향성에 0.9, 새로운 경향성에 0.1을 곱하여 더해주는 것으로 10일간의 데이터를 활용하여 평균을 취해주는 것과 같은 역할을 한다고 생각할 수 있습니다.
지수 가중 평균은 초기값이 편향되는 문제가 있습니다. 초기에는 과거의 경향성이 없기 때문에 초기값이 실제값과 다른 분포를 갖게 됩니다. 베타가 0.9이고 초기값이 10이라고할때 초기값이 10이어야 하지만 지수 가중 평균에 의하면 0.1에 10이 곱해진 1이 초기값이 되어버리기 때문입니다. 이 문제를 보완하는 것이 편향보정(bias correlation)입니다.
편향보정(bias correlation)은 초기 값에 따른 편향으로 인한 실제 데이터 값과의 차이를 실제 데이터와 유사하도록 보정해주는 것으로 Vt값에 (1-b^t)값으로 나누어주는 것으로 해결합니다.
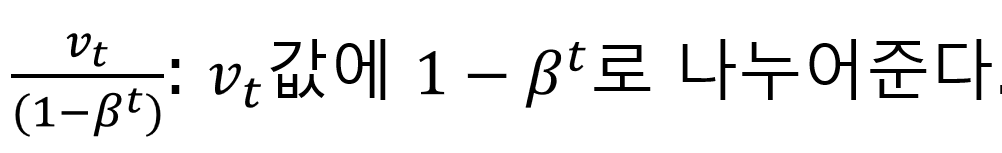
t가 커질수록 분모가 0에 수렴하기 때문에 초기값만 보정되고 이후엔 Vt와 거의 비슷한 값을 가지게 됩니다.
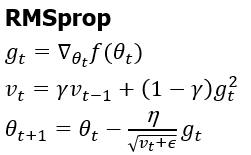
RMSprop은 Adagrad에서 Gt부분에 지수 가중 평균을 활용하여 오래된 기울기 값을 거의 반영하지 않고 최근 기울기 값을 많이 활용하여 Gt가 계속해서 커지는 것을 방지하고 일정수준 이상으로 누적되며 점점 커지는 것을 방지하여 Adagrad의 단점을 보완했습니다.

Adam(Adaptive Moment Estimation)은 Momentum과 Adaptive Gradient를 모두 활용하는 방법이다. 경사하강법이 가지고 있는 두가지 문제점인 local minimum에 빠질 수 있다는 문제와 learning rate에 민감하다는 문제를 모두 해결하려 노력한 방법으로 Momentum과 Adaptive Gradient와 지수 가중 평균과 편향 보정을 활용하여 현재에 가장 많이 사용되는 최적화 기법입니다.
학습 테크닉
배치 정규화(Batch Normalization)
Internal Covariate Shift
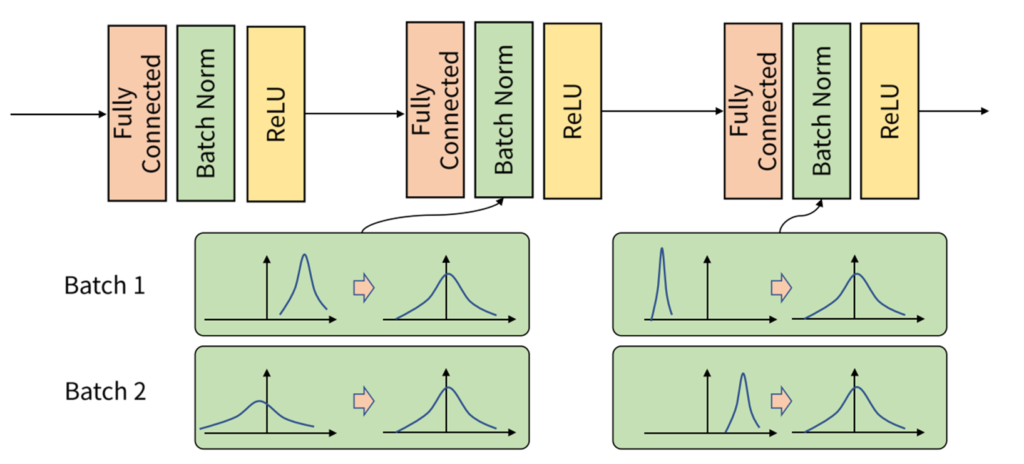
학습을 할때 학습과정에서 미니 배치마다 입력 데이터의 분포가 달라지게 되는 것을 Internal Covariate Shift라고 합니다.
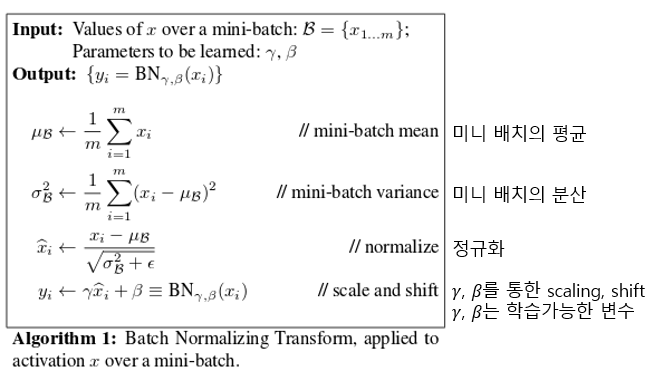
배치 정규화는 위의 Internal Covariate Shift문제를 해결하기 위한 방안으로 각 배치별로 평균과 분산을 이용하여 정규화하는 것입니다. 이때, 감마와 베타를 learnable parameter로 두어 scale과 shift를 학습합니다.
Inference시에는 학습때 학습된 감마와 베타를 통한 평균과 분산을 이용하여 정규화를 수행합니다.
배치 정규화는 감마와 베타를 활용하기에 비선형성질을 유지하면서 학습할 수 있고, Internal Covariate Shift를 해결했다. 정규화를 해주기에 regularization의 효과도 있기 때문에 drop out과 같은 기법이 필요없다는 특징이 있습니다.
박성준 연구원님, 정리글 잘 읽었습니다. 간단하게 배치 정규화에 관한 질문 몇 개 남기겠습니다. 자세한 답변 기대하겠습니다.
박성준 연구원님께서 정리해주신대로 배치 정규화는 internal covariant shift를 해결하기 위해서 제안되었습니다. 이는 입력 데이터 분포가 층마다 달라지는 것입니다.
1. 공변량 시프트 문제는 결과적으로 딥러닝 학습에 있어서 어떤 문제점을 가져오게 될까요?
2. 박성준 연구원님이 첨부해주신 사진에서는 Batch Norm이 FC layer와 ReLU 사이에 위치해 있습니다. 왜 저기에 배치 정규화가 있나요? 순서가 바뀌면 안되나요? 안된다면 왜 안될까요?
3. CNN모델을 작성하고자 할 때, Conv layer와, activation(ReLU)과, dropout과, batch norm을 적용시키려고 합니다. 각 모듈의 순서를 어떻게 구성하는것이 좋을까요? 그 이유는 무엇일까요?
해당 답변을 고민하면서 내용들을 더 깊게 이해하는 계기가 되기 바랍니다.
첫 X-Review 작성하시느라 수고하셨습니다.
질문의 순서대로 답변하겠습니다.
1. 공변량 변화가 문제가 되는 이유는 딥러닝 학습에서 깊이가 깊어져 연산이 누적될수록 가중치의 작은 변화가 쌓이고 쌓여 큰 변화로 나타날 수 있기에 배치 정규화를 하지 않는다면 데이터의 분포를 영향을 받아 가중치가 의도대로 갱신되지 않을 수 있고 이 현상이 누적되면서 학습을 방해할 수 있기 때문입니다.
2. 배치 정규화의 위치는 활성화 함수 이전에 적용되는 것이 취지에 맞는 가장 바람직한 위치이기 때문입니다. 배치정규화의 목적은 연산 결과의 분포를 원하는 방향으로 조정해주는 것이기 때문입니다. 활성화 함수를 거치게 되어 분포가 바뀌기 전인 convolution을 거친 직후에 적용해야합니다. 하지만 이때, 배치 정규화는 데이터의 분포를 평균이 0, 표준편차 1이 되도록 정규화를 해주는데 ReLU활성화함수를 거친다면 정규화를 한 값의 절반이 0으로 소실되기에 이를 방지하고자 scale, shift를 조정해줍니다. 이때 scale, shift는 학습을 통해 적절한 값으로 학습됩니다. 그렇기에 순서를 바꾸면 안됩니다.
3. 2번 답변에 의하면 Conv layer -> Batch Norm -> Activation(ReLU) 순서로 적용되어야합니다. Dropout은 Activation(ReLU)이후에 적용되어 다음 계층의 연결을 조정합니다. Dropout은 신경망의 연결 일부을 끊어 신경망의 과적합을 방지하고 일반화에 도움을 주는 방법이므로 계층에서의 연산에는 관여하지 않기에 활성화 함수까지 연산이 끝난 이후 다음 계층의 연결에 관여하기 위해 마지막에 적용됩니다. 최종 순서는 Conv layer -> Batch Norm -> Activation(ReLU) -> Dropout 입니다.
지나치거나 놓칠 수 있는 부분을 질문으로 남겨주셔서 한번 다시 복습하며 깊게 공부할 수 있었습니다. 좋은 질문 감사합니다.