딥러닝 기초 정리

안녕하세요. 저는 첫 X-Review로 딥러닝의 기초에 대해서 정리한 내용을 쓰기로 했습니다. 딥러닝 기초에 모든 내용을 정리한게 아니라 제가 모르고 있거나 더 알고 싶은 내용 위주로 정리해보았습니다. 그럼 시작하겠습니다.

먼저 제가 알아볼 파트는 크게 3가지로 활성화 함수,손실 함수 , 최적화 알고리즘입니다

활성화 함수

먼저 신경망의 활성화 함수로 선형 함수가 아니라 비선형 함수를 사하는데 왜 선형함수를 사용하면 안되는지 살펴보겠습니다.

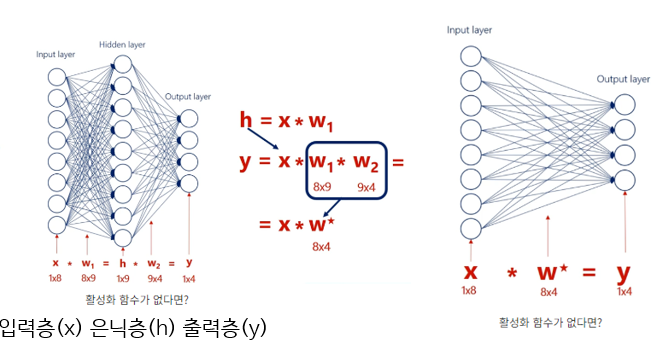
왼쪽 그림처럼 입력층 은닉층 출력층이 있고 각각의 층을 x,,h,y라고 한다면 h는 입력층에 가중치w1을 곱한 형태로 표현될 것이고

Y= h에 w2를 곱한 값으로 표현이 될텐데 여기서 w1과 w2의 크기를 살펴보면 각각 8*9. 9*4의 크기를 가집니다. 이는 8*4의 크기로 다시 표현될 수 있기 때문에

이 그림이 오른쪽 그림 처럼 은닉층이 없는 형태로 표현됩니다. 이로 인해 선형함수로는 층을 깊게 쌓을 수 없기 때문에 비선형 함수를 사용해야합니다.

그래서 비선형함수의 활성화 함수를 사용해야하고 이제 그것들의 종류에는 무엇이 있는지 살펴보겠습니다.

Sigmoid, tanh

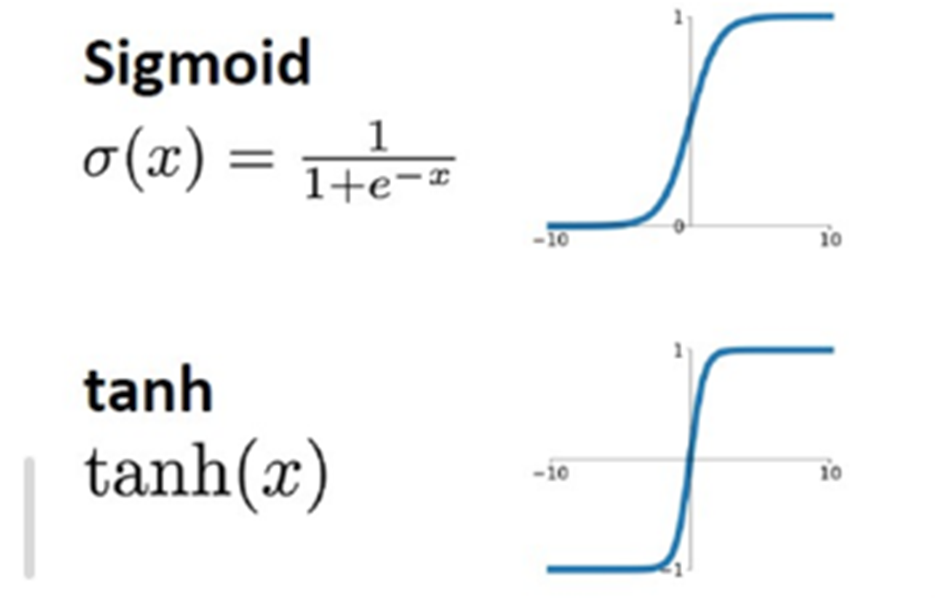
먼저 시그모이드 함수 입니다. 시그모이드는 입력값을 0에서 1사이로 출력하는 함수 입니다. 그리고 출력값이 0~1사이라는 단점을 보완한 함수가 하이퍼볼릭 함수인데 이 2개의 함수에는 공통적인 단점이 존재하는데 모두 기울기 소실 문제를 가지고 있다는 것입니다. 왜 기울기 소실 문제가 발생하는지 수식으로 살펴보겠습니다.

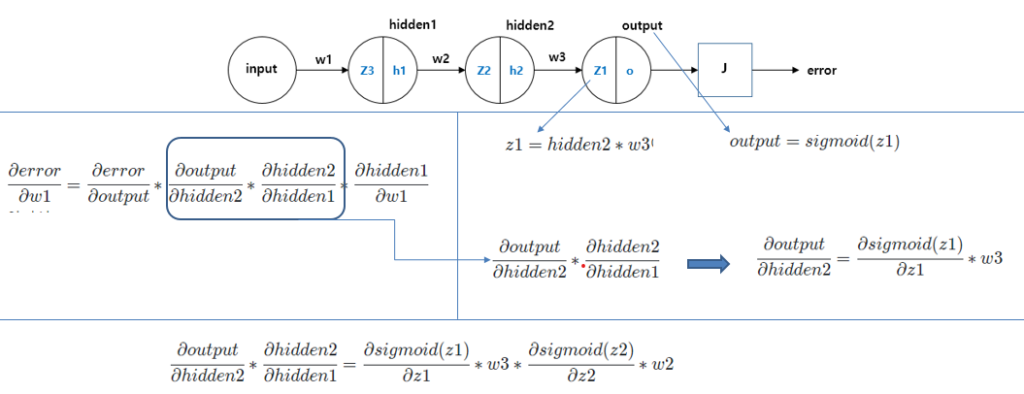
설명을 위해 인공신경망의 구조을 단순하게 하여 설명하겠습니다 이 신경망에 인풋이 들어가고 순전파를 통해 예측값을 구하고 에러를 구햇다면 가중치를 업데이트 하기위해 역전파를 수행해야합니다. 이 과정을 체인룰에 따라 식을 다시 쓸 수 있고 박스 친 부분만 따라 때어내어 보면 식이 화살표에 나온 것처럼 변형이됩니다. 그리고 맨 아래에 있는 식을 보면 layer가 진행될 수록 sigmoid 함수가 연속으로 곱해지는 것을 알 수 있습니다. sigmoid 함수의 미분은 0 ~ 0.25로 1보다 작으므로 곱해지는 횟수가 많을 수록 값은 점점 더 작아지게 됩니다. 즉 layer가 많을 수록 기울기의 값은 더 작아지므로 gradient vanishing문제가 발생하게 되는 것 입니다.

ReLU

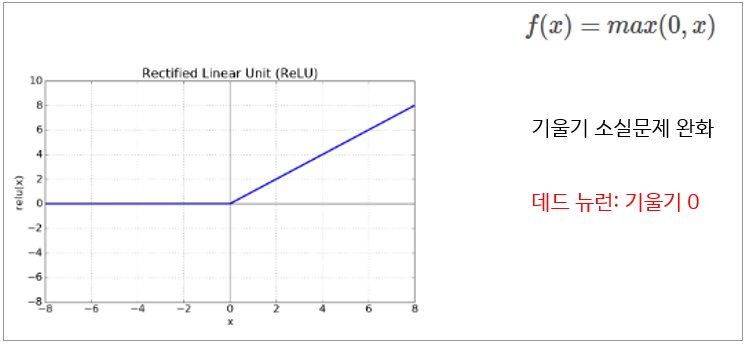
그래서 기울기 소실문제를 어느정도 해결한  함수가 ReLU 함수입니다. ReLU는 음수에서는 출력값이 0이고 양수서는 값이 그대로 나온다는 특징을 가지고 있습니다.

ReLu같은 경우 역전파를 시킬때 활성화함수의 기울기 값이 1이기 때문에 기울기 소실문제를 어느 정도 해결하였지만 입력값이 0일때는 값이 0이고 기울기가 전파가 안되는 문제를 가지고 습니다.

LeakyReLU , ELU

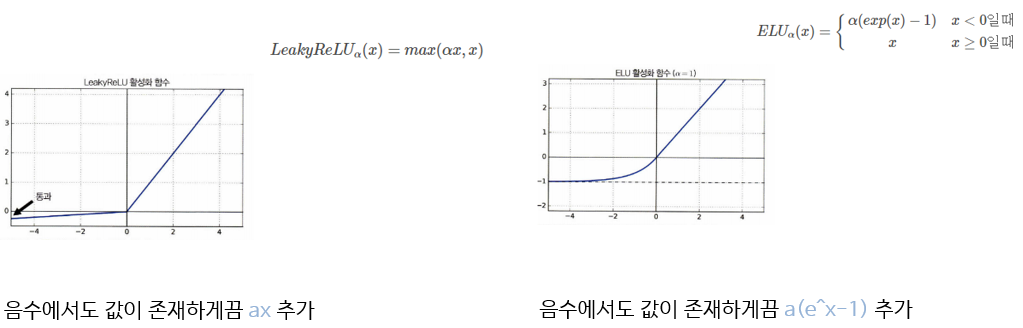
그래서 이를 보완한게 리키 렐루와 ELU입니다. 리키 렐루는 음수에서도 값이 존재하게끔 ax라는 직선이 추가되었고 이는 렐루의 입력이 0 일때 출력이 항상0 이되서 기울기 소실이 발생하는 문제를 어느 정도 해결할 수 있고

ELU도 마찬가지로 양수이든 음수이든 모든 범위에서 안정적인 기울기를 가져서 기울기 소실 문제를 완화할 수 있습니다.

Maxout

이 부분은 ‘https://blog.naver.com/laonple/220836305907’의 블로그를 참조해서 작성했습니다.

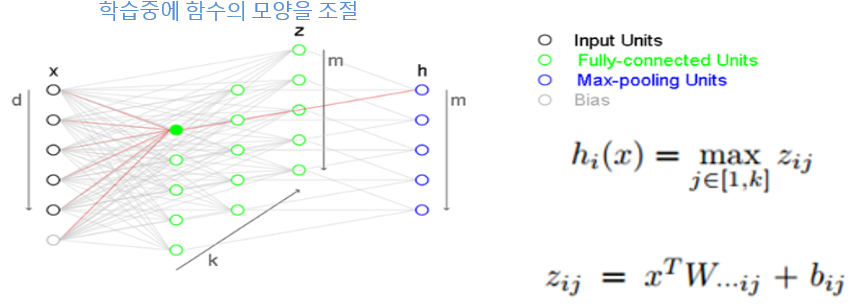
Maxout함수같은 경우 다른 활성화 함수와 다르게 학습중에 함수의 모양을 조절할 수 있는 함수입니다. 맥스아웃을 그림으로 살펴보면 맥스아웃의 히든레이어는 일반적인 히드레이어가 1개의 레이어로 구성되어있는것과 달리 2개의 레이어로 구성되어있습니다. 초록색 영역이 아핀 function을 수행하는 부분이고 파란색 영역이 초록색 영역에서 최댓값을 뽑아낸 부분입니다.

녹색영역을 전통적인 히든레이어처럼 활성화함수가 있는게 아니라 단순히 x에 weight와 bias를 더해서 구한 것이기 때문에 아핀 함수라고 부릅니다. 그림과 같이 k개의 열에서 동일한 위치에 있는 노드 중에서 최고값을 파란색 영역에서 취하게 됩니다.

Qi Wang의 논문에서는 Maxout이 렐루보다 성능이 좋은 이유를 경로의 관점에서 해석을 하였는 maxout은 여러 개의 경로중 하나를 선택할 수 있고 기울기가 역전파 되는 방향도 그 경로로만 전파가 되기때문에 이것은 학습 샘플로부터 얻은 정보를 spars한 방식으로 encoding이 가능하다는 뜻이 됩니다. Relu도 sparse한 성질이 있긴 하지만 경로 선택에 있어서는 제한적이기 떄문에 relu 경우에 과적합될 가능성이 높다고 합니다.

손실함수

손실 함수에는 여러 종류가 있지만 저는 그 중에서 Cross Entropy Loss(CE Loss)를 중점적으로 살펴보겠습니다. 하지만 CE Loss를 이해하기 위해서는 Softmax와 Negative Log Likelihood(NLL)에 대한 이해가 필요하기 때문에 Softmax -> Negative Log Likelihood -> Cross Entropy Loss 순으로 알아보도록 하겠습니다.

Softmax와 NLL 함수는 ‘https://gaussian37.github.io/dl-concept-nll_loss/’의 블로그를 참고해서 작성하였습니다.

Softmax

Softmax함수는 보통 신경망의 끝 부분에 위치하고 있으며 출력 값을 0~1 사이의 확률 값으로 나타내기 위해 사용이 됩니다. 이러한 특성 때문에 multi-class classification과 같은 문제를 풀 때 자주 사용이 됩니다.

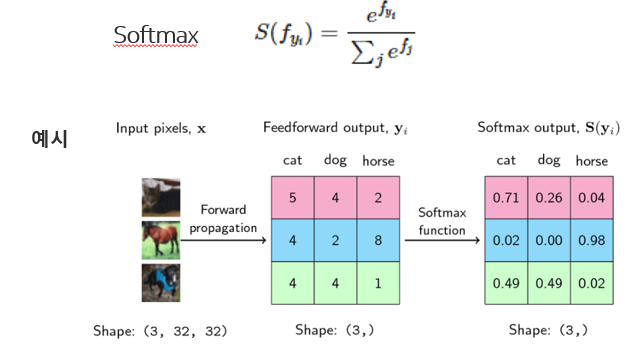
제가 참고한 블로그의 예시로 Softmax와 NLL 함수가 어떻게 사용되는지 살펴보겠습니다. 먼저 그림과 같이 3개의 이미지 고양이, 말, 개가 있다고 가정하겠습니다. 먼저 고양이 이미지 입력을 넣었을 때, 출력은 분홍색, 말은 파란색, 개는 초록색에 해당합니다. 가운데 행렬이 출력값에 해당하며 행렬의 첫번째 열은 고양이, 두번째 열은 개, 세번째 열은 말에 해당하며 가장 큰 값을 가지는 클래스가 선택됩니다. 가운데 행렬에서 첫 번째 행을 살펴보면 가장 큰 값이 5이기 때문에 고양이를 클래스로 선택하고 두 번째 행에서는 가장 큰 값이 8이기 때문에 8의 열에 해당하는 말을 클래스로 선택하게 됩니다. 마지막 3번째 행에서는 값이 4로 같은 부분이 생겨서 무엇을 클래스로 선택할지 애매해지지만 중요한 것은 출력 값을 확률 값으로 바꾸고 클래스에 해당하는 확률 값들을 모두 더했을때 총합이 1이 된다는 것입니다.

Negative Log Likelihood(NLL)

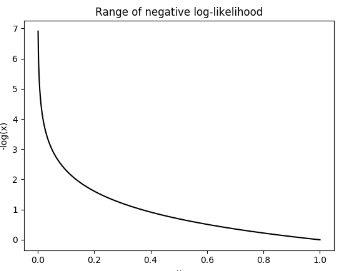
이제 Softmax를 취한 값을 통해 Loss를 계산해 주어야 하는데 이때 사용되는 Loss 함수가 Negative Log Likelihood(NLL)입니다. NLL 같은 경우 아래의 그래프처럼 로그 함수의 범위가 0~1이고 이 부분에 음수를 곱한 형태로 그래프가 나타나게 되는데 만약 정답인 클래스가 입력으로 들어갈 경우 1에 가까워 질수록 값이 작아지는 특성이 있기 때문에 마치 Loss함수처럼 사용할 수 있는 것입니다.

이러한 특성을 이용해서 softmax와 NLL을 이용해서 Loss함수를 만들 수 있습니다. 그 방법에는 총 2가지가 있습니다. 첫 번째 방법은 argmax를 취하는 방법이고 두번째 방법은 모든 logit에 적용하는 방법이 입니다.

첫 번째 방법에서는 정답 클래스에 해당하는 확률에 -log를 취해서 Loss를 구하고 각 행마다 클래스에 해당하는 출력 값의 Loss를 더해서 Total loss를 구하게 됩니다.

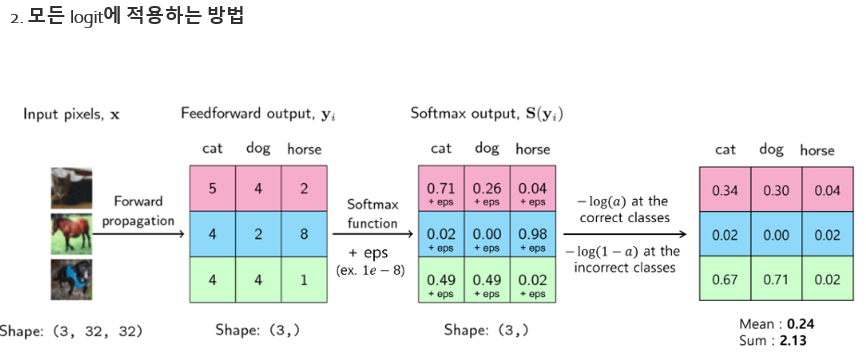
파이토치에서는 2번째로 모든 logit에 적용하는 방법이 사용된다고 합니다.

위 그림과 같이 정답에 해당하는 클래스에는 -log(a)를 취하고 정답이 아닌 클래스에는 -log(1-a)를 취합니다. 정답이 아닌 클래스에 -log(1-a)를 취하는 이유는 정답이 아닌 클래스의 확률 값은 0에 가까워져야 하기 때문에 첫 번째 방법과 다르게 정답이 아닌 클래스도 Loss에 포함시켜 모든 확률 값을 고려하게 됩니다.

최종적으로 계산된 모든 NLL Loss에 대하여 sum 또는 mean 연산을 취하게 되면 Loss가 하나의 스칼라 값으로 도출되게 됩니다.

Cross Entropy Loss(CE Loss)

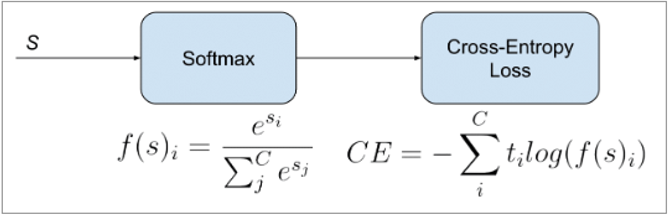
CE Loss는 앞에서 살펴본 softmax와 NLL가 결합현 형태로 두 확률 분포 p와 q의 차이를 구하는데 사용이 됩니다. 이 식에 대한 해석은 레이블들의 분포에 대한 손실의 기대 값을 의미합니다. 때문에 CE Loss는 다중 클래스 분류에서 가장 흔히 사용되는 손실입니다.

최적화 기초

최적화 알고리즘은 딥러닝 모델을 학습시킬때 사용되는 알고리즘으로 모델의 손실함수를 최소화하고 가중치 및 편향을 업데이트 하는데 사용됩니다.

경사하강법( GD)

경사 하강법은 가장 기본적인 최적화 알고리즘을 손실함수의 기울기를 이용하여 가중치와 편향을 조정합니다. 그리고 학습률을 이용하여 가중치를 얼마나 업데이트 할지 결정합니다. 하지만 경사하강법은 전체 데이터 세트를 한 번에 처리하므로 계산 비용 높다는 단점이 있는데이를 보안한 것이 SGD입니다.

확률적 경사하강법( SGD) : 전체 학습 데이터를 사용하는 대신, 각 학습 데이터 포인트에 대해 가중치를 업데이트하는 방식으로 속도를 높이는 경사 하강법의 변형

미니배치 확률적 경사 하강법(Mini-batch SGD): 전체 데이터를 미니배치로 나누어 가중치를 업데이트하는 방식으로, SGD의 불안정성을 줄이면서 빠른 학습을 제공

gd , sgd, mini batch sgd의 공통적인 단점으로 로컬 미니마 문제를 가지고 있습니다. 이른 보안한 방법으로 Momentum이 있습니다.

Momentum

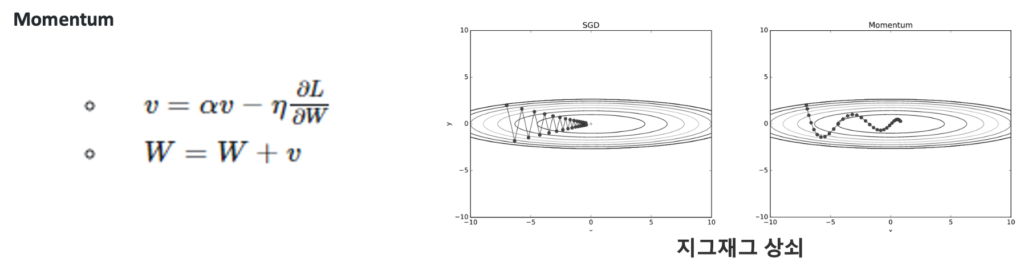
모멘텀은 물리에서 가져온 개념으로 관성으로 이해를 할 수 있습니다.

위식에서 SGD와 달라진점은 a*v인데요 av는 기울기 방향으로 힘을 받아 물체가 가속된다는것을 의미합니다. 그래서 가중치를 업데이트 할때 이전의 속도도 고려해주기 때문에 local minima에 걸리더라도 탈출을 할 수 있게됩니다.

또한 특정방향으로 업데이트가 자주 이루어 진다면 그 방향에 속도가 생겨서 지그재그로 왔다 갔다 하는 상황이 줄어들어 오른쪽 그림처음 지그재그를 상쇠하며 앞으로 나아갈 수 있습니다.

NAG

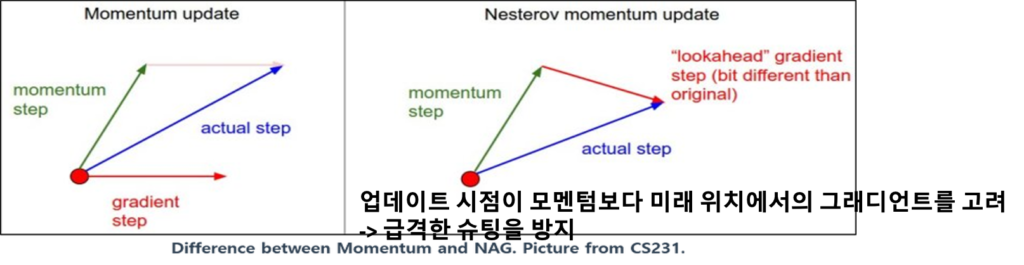
그 다음이 nag인데 이 알고리즘을 비교 해보면 모멘텀은 현재위치에서 기울기를 구하고 이전 속도를 구해서 그 벡터를 더한 방향으로 이동하지만 NAG 같은 경우에는 이전 속도를 가져오고 이전 속도로 갔을 때의 지점에서 기울기를 구한 후에 두 가지 벡터를 더하게 됩니다.

NAG의 주요 이점은 업데이트 시점이 모멘텀보다 미래 위치에서의 그래디언트를 고려하기 때문에 미래 위치에서의 그래디언트가 크게 이탈하는 경우 더 정확한 업데이트를 제공할 수 있습니다. 이로인해 NAG는 모멘텀보다 수렴 속도가 빠를 수 있습니다.

Adagrad

이제 부터는 고정된 learning rate이 아닌 상황에 따라 다르게 적용되는 Adaptive learning rate를 활용한 방법론입니다.

Adagrad는 이전 그레이디언트의 제곱을 누적하여 각 매개변수의 학습률을 계산합니다

RMSprop

AdaGrad는 학습이 진행될 때 학습률이 꾸준히 감소하다 나중에는 0으로 수렴하여 학습이 더 이상 진행되지 않는다는 한계가 있습니다. RMSProp은 이러한 한계점을 보완한 방법론입니다.

RMSProp은 이전 time step에서의 기울기를 단순히 같은 비율로 누적하지 않고 지수이동평균(Exponential Moving Average, EMA)을 활용하여 기울기를 업데이트합니다. 즉, 알고리즘의 핵심은 가장 최근 time step에서의 기울기는 많이 반영하고 먼 과거의 time step에서의 기울기는 조금만 반영하는 점입니다.

Adam

Adam은 Momentum과 RMSProp의 장점을 결합한 알고리즘입니다.

M^이나 g^은 초기의 모멘텀 값이 0 으로 초기화되는 경우를 방지하기 위해 bias-correction이 적용된 것입니다.

학습테크닉

Normalization과 Regularization

이 부분은 ‘https://gaussian37.github.io/dl-concept-regularization/’의 블로그를 참고했습니다.

학습 테크닉으로 Normalization과 Regularization 있는데 각각 데이터의 스케일을 조정하는 작업과 predict function의 복잡도를 조정하는 작업을 의미합니다.

저는 Regularization를 중점으로 딥러닝에서 많이 사용되는 l1,l2 Regularization에대해 살펴보았습니다.

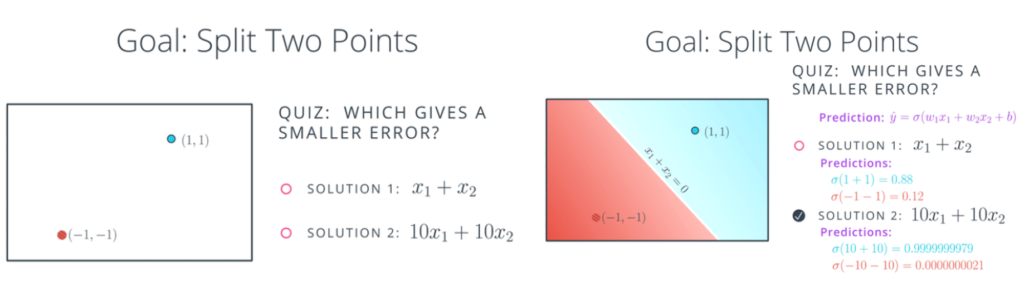
간단한 예시를 통해서 Regularization이 왜 필요한지 그리고 predict function의 복잡도를 조정하는 작업이 무슨 의미인지 살펴보겠습니다.

먼저 설명을 위해 왼쪽 아래 그림처럼 파란색 점과 빨간색 점을 나누는 라인을 구할때 sol1과 sol2 중 어떤 모델의 에러가 더 작을 지 살펴보면 일단 둘은 같은 직선을 가지지만 에측 값은 오른쪽 그림과 같이 나옵니다. 여기서는 sol2의 에러가 더 작기에 sol2가 더 좋은 모델처럼 보이지만 여기에는 또 다른 문제가 있습니다.

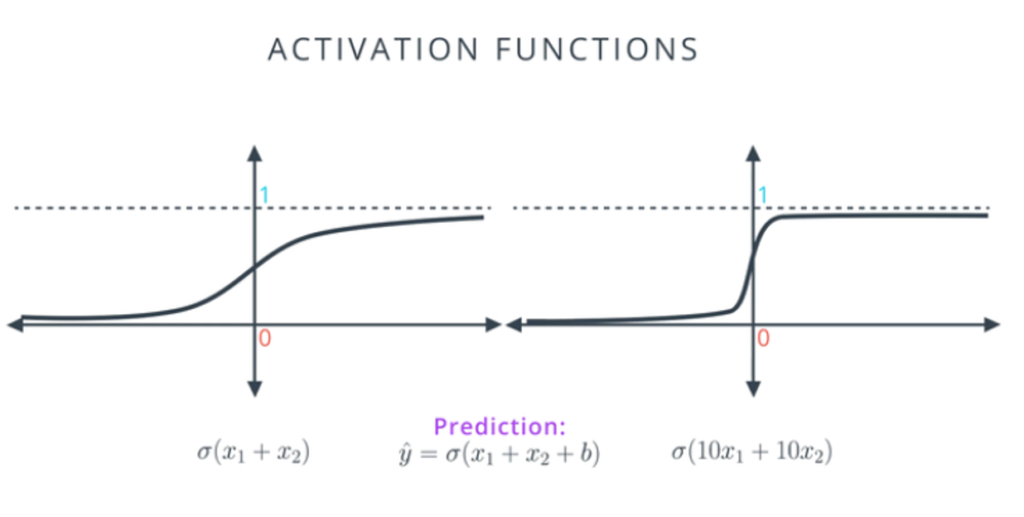
그림은 각각 sol1,2모델에 시그모이드를 적용한 그래프 입니다. 왼쪽 그래프에 비해 오른쪽 그래프는 x=0주위로 급격한 기울기를 가지고 x의 값이 커지거나 작아질때 기울기가 급격하게 0으로 수렴함을 알 수 있습니다. 학습을 하기위해서는 기울기가 중요한데 기울기가 급격하게 0으로 수렴해버리면 학습이 제대로 이루어지지 않습니다.

만약 오른쪽 모델을 선택하였을때 점들이 오분류 되어있다면 학습을 통해 모델을 수정하기 어려워 지는 것 입니다.

이를 해결하는 방법이 weight에 패널티를 주는 것입니다.  그 방법에는 L1처럼 가중치의 절댓값을 모두 더하는 방식과 L2처럼 가중치의 제곱을 더하는 방식이 있고 여기서 감마는 패널티를 얼마나 줄지 결정하게 됩니다.

L1, l2 의 선택 기준에는 무엇이 잇는가 살펴보면 l1을 적용하게 되면  vector들이 sparse 해지는 경향이 있습니다. 이 의미는 너무 많은 가중치가 있을때 더 중요한 weigh만 선택하고 나머지는 0으로 만드는 효과를 얻을 수 있습니다.

L2의 경우 sparse vector를 만드는게 아니라 모든 가중치를 균등하게 작게 유지하는 것입니다.

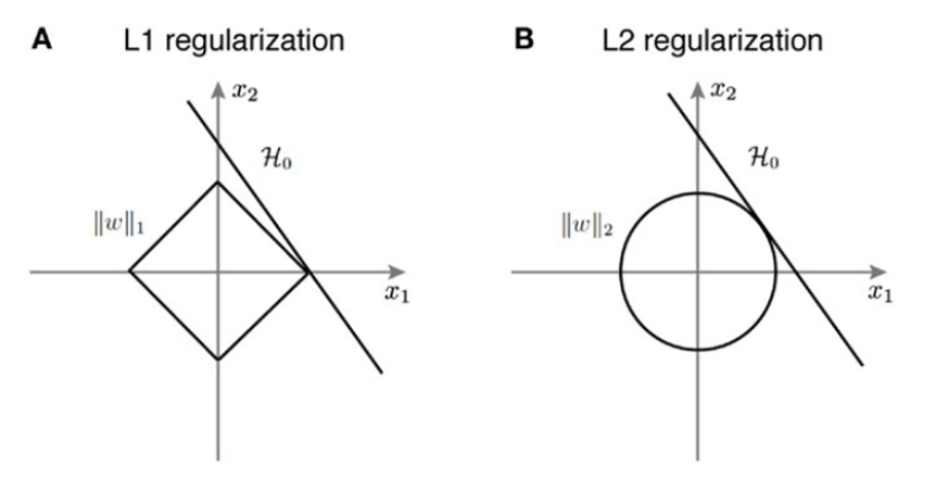
왜 l1을 적용했을때 sparse한 벡터가 만들어지는지 살펴보겠습니다.

먼저 가중치 x1,x2가 있고 왼쪽 마름모가 l1의 분포를 나타내고 h가 에러를 최적화 시키는 솔루션이라고 가정을 한다면 l1,l2의 분포와 h가 한점에서 만나는 점이 최적화 하는 해가 될 것입니다.

이 그림처럼 만나는 지점이 축위에 있음을 확인 할 수 잇는데 이는 솔루션의 해가 중 하나가 0이 되었다는 것을 의미합니다. 즉 절댓값 함수의 형태로 인하여 sparse한 vector가 생성되게 되는것입니다.

그래서 정리를 하자면 로스 함수에 regularization항을 추가로 넣어서 모델의 복잡도가 지나치게 높아져서 과적합 되는 것을 방지하고 모델이 더 일반화 될 수 있게 해줍니다.

Dropout

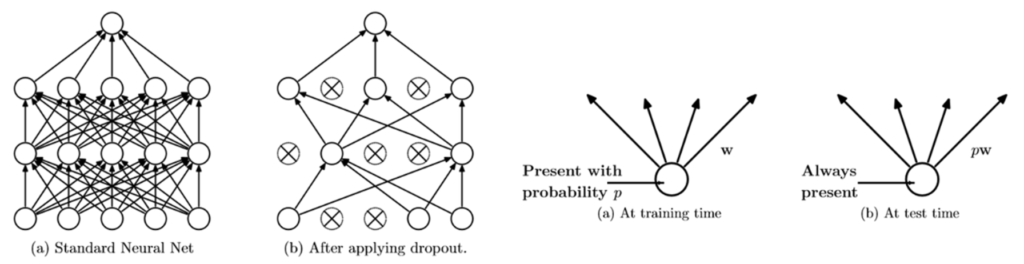
Dropout은 이 그림처럼 네트워크의 일부를 생략하는 것입니다. 먼저 드롭 아웃이 학습을 할 때에는 p의 확률로 학습시킬 노드들을 각 층에서 정한 뒤에 학습 시키고 예측을 할 때에는 모든 노드를 활성화 시켜서 예측하게 됩니다. 하지만 그냥 모든 노드를 활성화 시키면 문제가 생기게 됩니다. 훈련 때 사용했던 노드 수와 테스트 때 사용할 노드 수가 다르기 때문에, 훈련한 대로의 결과를 얻지 못할 수 있습니다. 이전 층이 100차원이었고 dropout 비율이 0.3이었다면 훈련때 마다 다음 층의 입력들은 약 70개의 입력을 받으며 훈련될 것입니다. 그런데 예측 시 100차원을 입력으로 사용하게 되면 값의 크기에 문제가 생기게 됩니다. 그래서 크기 조정(rescale)을 해주는 과정을 추가해줘야 합니다. 따라서 각 뉴런에 확률 p를 곱해서 기댓값을 얻는 방식으로 노드의 가중치를 계산하게 됩니다.

Dropout 의 부가 효과

Dropout을 사용하면 사용하지 않을 때보다 좀 더 선명한 특징(salient feature)을 끌어낼 수가 있게 됩니다. 그 이유를 살펴보면 dropout을 사용하지 않았을 때는 모든 노드들이 Loss를 줄여나가기 위해 서로에게 의존하는 공조 현상이 일어날 수 있다고 합니다. 하지만 dropout을 적용시켜서 뉴런들을 무작위로 생략시키면 parameter들이 서로 동화되는 것을 막을 수 있어서 좀 더 의미 있는 특징들을 더 추출 할 수 있다고 합니다. 

또한 Dropout은 훈련 중에 다양한 모델을 학습하는 효과를 갖습니다. 각 훈련 단계에서 다른 뉴런 집합이 활성화되므로 여러 모델을 평균한 것과 유사한 효과를 얻을 수 있습니다. 이는 모델의 일반화 능력을 향상시키고 앙상블 효과를 주는 것과 비슷합니다.

Batch Normalization

과적합을 줄이는 또 다른 방식으로 Batch Normalization이 있습니다. Batch Normalization 사용하는 이유는 internal covariate shift 문제를 피하기 위함입니다.

internal covariate shift 가 무엇인지 살펴보겠습니다. covariate shift는 머신 러닝에서 왼쪽 그림과 같이 training data와 test data의 data distribution이 다른 현상을 의미합니다.

우리가 training dataset을 학습시킨다고 가정하면 입력이 주어졌을때 layer 거치면서 이전 레이어의 출력이 다음 레이어의 입력으로 들어갈텐데 아무런 규제 없이 가중치들이 제멋대로 학습하다보면 매개변수의 범위가 넓어질 수 있습니다. 그리고 매개변수의 값들의 변동이 심해지게되는 현상을 internal covariate shift라고 합니다.

Batch Normalization의 방법을 살펴보면 먼저 mini-batch의 평균과 분산을 구해 줍니다 이후에 구한 평균과 분산으로 정규화를 시킵니다. 그렇게 되면 입력의 분포는 -1~1로 됩니다. 이후에 스케일과 시프트에 해당하는 감마가 곱해지고 베타가 더해집니다. 이 단계가 추가되는 이유는 정규화 단계에서 입력의 분포는 -1~1이 되는데 여기에서 relu와 같은 활성화 함수를 사용하게 되면 음수에 해당하는 부분이 0이 되기 때문에 감마와 베타를 곱하고 더해서 이를 방지하는 역할을 합니다. 그리고 감마와 베타는 학습을 통해서 갱신이 됩니다.

참고 블로그

https://gaussian37.github.io/dl-concept-nll_loss/ , https://blog.naver.com/laonple , https://ratsgo.github.io/blog/categories/ , https://ko.d2l.ai/index.html , https://onevision.tistory.com/entry/Optimizer-%EC%9D%98-%EC%A2%85%EB%A5%98%EC%99%80-%ED%8A%B9%EC%84%B1-Momentum-RMSProp-Adam