[ICCV 2023] ProbVLM : Probabilistic Adapter for Frozen Vision-Language Models

Before Review

원래 제가 한동안 관심을 가지던 연구 주제는 Video Scene Segmentation이지만, 실험에 소요되는 시간이 길기도 하고 아직 뚜렷한 contribution이 나오지 않아서 제출 계획은 ECCV로 미루고 지금은 김현우 연구원과 Multimodal Representation을 활용하는 Weakly Supervised Temporal Action Localization 연구에 합류하게 됐습니다.

저희가 현재 관심을 가지고 있는 방향은 Video + Text 인 Multimodal 상황에서 Probabilistic Representation을 활용하는 방법을 고민하고 있습니다.

이번 ICCV 2023에 Video + Text는 아니고 Image+Text인 상황에서 Probabilistic Representation을 고민하는 방향의 논문이 나와버렸네요. 논문 내용이 조금 어렵긴 했지만 꼭꼭 씹어 먹었습니다.

리뷰 시작하겠습니다.

Preliminaries

 Contrastive Language-Image Pre-training (CLIP)

워낙 유명해서 다들 아실 거 같지만 그래도 간단하게 정리하고 넘어가겠습니다. CLIP은 OpenAI가 공개한 Vision-Language Pretrain 방법론 입니다.  인터넷 웹에서 수집된 4억 개의 (이미지, 텍스트) 쌍을 이용하여 사전 학습을 수행한 연구 입니다.

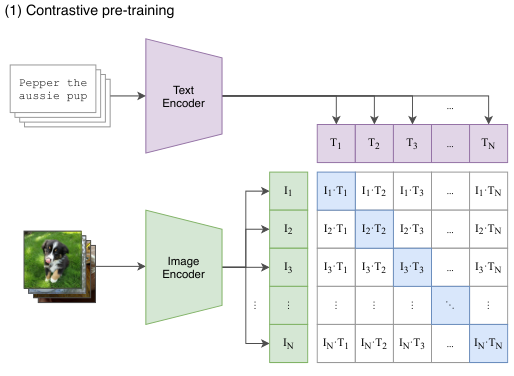
기존 Contrastive Learning의 패러다임을 아신다면 이해가 빠르겠지만 CLIP은 결국 어떤 이미지와 어떤 텍스트가 올바른 쌍을 가지는지 맞추는 방식으로 학습이 진행 됩니다.

이 과정에서 Text Encoder와 Image Encoder는 동일한 embedding space를 가지게 됩니다.

무슨 말이냐면 이미지-텍스트 쌍을 올바르게 찾는 문제를 풀다 보면 Positive pair간 Image-text representation이 유사해질 수밖에 없고 Negative pair 간 representation은 서로 다른 구별력을 가질 수 밖에 없습니다.

대용량 이미지-텍스트 쌍을 가지고 이러한 작업을 반복하다 보면 굉장히 generalization이 잘 된 image-text encoder를 얻을 수 있는 것 입니다. 많은 논문들이 이렇게 사전 학습된 CLIP Encoder를 활용하여 다양하게 후속 연구를 진행하고 잇습니다.

Probability Distribution

확률 분포는 보통 어떤 데이터나 사건이 관측 되었을 때 이를 설명해줄 수 있는 확률 밀도, 확률을 반환해주는 함수라고 배웠습니다. 이 때 확률 분포를 특정해주기 위해서는 확률 분포를 구성하는 parameter가 특정 되어야 합니다.

위의 함수는 정규분포에 해당하는 확률 밀도 함수 입니다.

해당하는 확률 밀도 함수의 독립 변수는 \mu(평균)와 \sigma(표준 편차)로 구성되어 있습니다.

즉, 위의 그래프 처럼 \mu(평균)와 \sigma(표준 편차)가 달라지면 분포도 달라지는 것이죠. 확률 분포를 특정하기 위해서는 확률 분포를 구성하는 parameter를 정의 해야 합니다. 그리고 이는 정의된 분포마다 다른 값을 가지곤 하죠.

정리하면 특정한 확률 분포를 추정하기 위해서는 확률 분포를 특정할 수 있는 parameter를 찾는 과정과 동일하다고 생각하시면 됩니다.

Probabilistic Embedding

위에서 확률 분포에 대해 실컷 설명을 했으니 이제 확률적 임베딩에 대해서 한번 설명을 해보도록 하겠습니다.

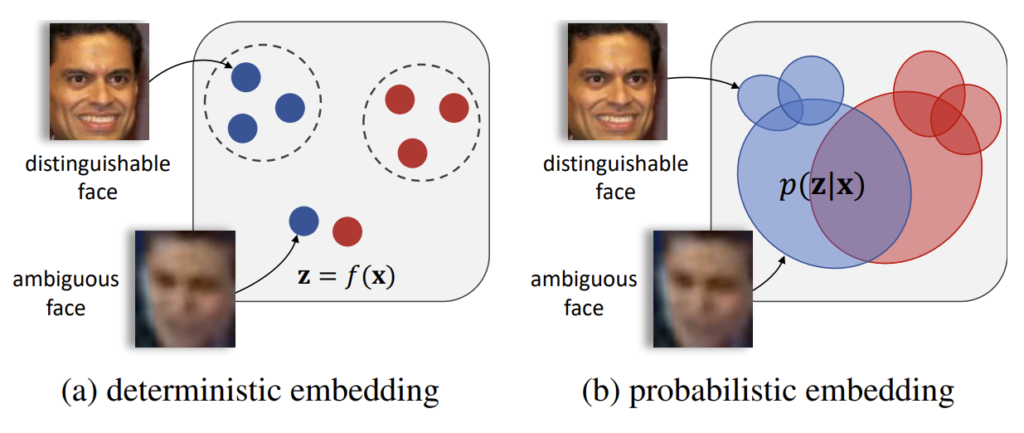
말 그대로 feature embedding을 probability distribution을 가질 수 있도록 하는 것 입니다. 그런데 이렇게 설명하면 조금 모호할 수 있으니 좀 더 설명을 드려보자면

우리가 입력 데이터 X를 가지고 있을 때 기존의 임베딩 z=f(X)은 하나의 deterministic한 vector로 정의가 되었습니다. 위의 그림 (a) 처럼 Embedding Space 상에서 단 하나의 point로 정의가 되는 것이라 보면 됩니다.

우리가 입력 데이터 X를 가지고 있을 때 이것을 정규 분포로 modeling 하고 싶다 가정해보겠습니다. 위에서 우리가 정규 분포를 특정하기 위해서는 어떤 parameter가 필요하다고 했었나요? 바로 \mu(평균)와 \sigma(표준 편차) 입니다. 즉, \mu(평균)와 \sigma(표준 편차)를 임베딩 시켜야 분포를 특정할 수 있는 것이죠.

• \mu = f_{\mu}(X)
• \sigma = f_{\sigma}(X)

그렇다면 이제 우리는 p(z|x) = N(\mu, \sigma^{2}) 이렇게 정의할 수 있는 것 입니다.

만약 우리가 특정한 특징 벡터가 필요한 것이라면 이제 분포로부터 샘플링을 진행하면 되겠죠. 평균과 분산을 적절한 weight로 combination 시키면 분포로부터 발생하는 샘플을 만들 수 있습니다.

• z^{(k)}= \sigma \cdot \epsilon^{(k)} + \mu

이렇게 평균으로부터 편차를 어느 정도 허용하면 특정 샘플을 만들 수 있고 이를 가지고 representation learning에 활용하는 것이 probabilistic embedding 방법 입니다. 여기서 중요한 것은 정말로 데이터를 잘 표현할 수 있는 분포를 만들 수 있도록 학습 가능한 f_{\mu}(x; \theta_{\mu}), f_{\sigma}(x; \theta_{\sigma})를 잘 최적화 하는 것이 목표겠네요.

Maximum Likelihood Estimation (MLE)

최대 우도법(MLE)은 관측된 표본집단을 활용하여 모집단을 설명할 수 있는 분포를 특정하는 수학적 기법 입니다.

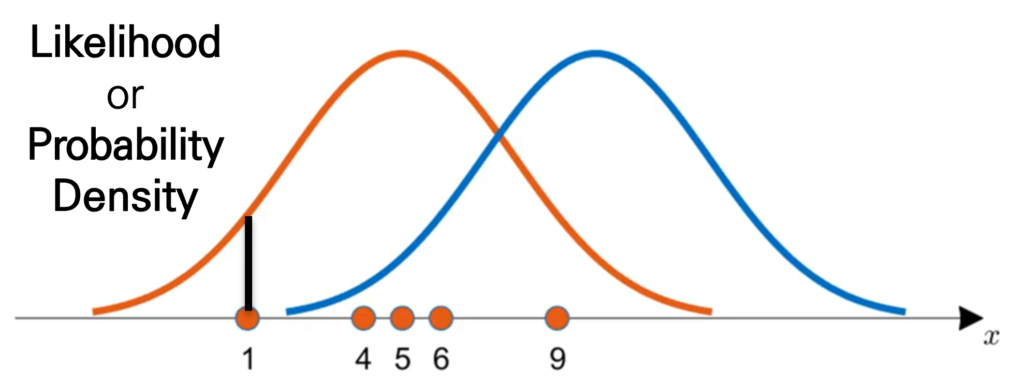
자 위의 그림과 같이 데이터가 x=[1,4,5,6,9] 이렇게 관측이 되었을 때 우리의 모집단을 정규분포로 가정해보겠습니다.

직관적으로 보면 x=[1,4,5,6,9]는 주황색 정규분포에서 관측 되었을 가능성이 높을까요 아니면 파란색 정규분포에서 관측 되었을 가능성이 높을까요?

주황색 정규분포에서 왔을 거 같은 느낌이 옵니다. 왜 그럴까요? 분포의 중앙에 데이터가 모여 있는 것이 어느 정도 평균을 형성하고 있는 것 같은 느낌이 들죠?

이를 좀 더 정량적으로 표현할 수 있는 방법이 있습니다. 바로 Likelihood Function 입니다.

우리가 정규 분포로 모집단을 가정 했다면 여러가지의 파라미터를 가정하여 다양한 정규분포를 가정할 수 있고 각각의 후보 분포에 대한 확률 밀도 값(likelighood)을 곱해서 수치적인 값을 정의할 수 있습니다.

계산된 높이를 더해주지 않고 곱해주는 것은 모든 데이터들의 추출이 독립적으로 연달아 일어나는 사건이기 때문입니다.

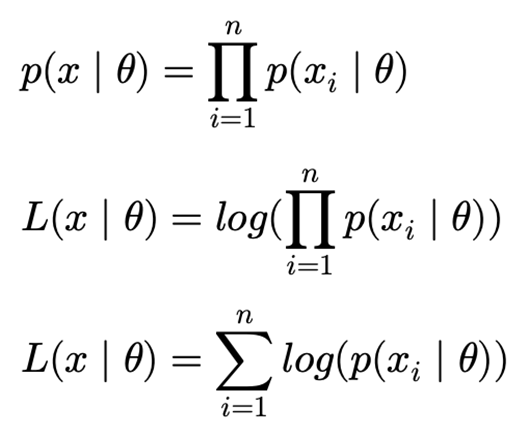
이 Likelihood Function은 결국 후보 분포를 결정할 수 있는 \theta에 대한 함수로 생각할 수 있습니다. 그리고 우리는 최대한 우리의 표본 집단을 잘 설명할 수 있는 즉, Likelihood Function이 최대가 되는 \theta를 찾음으로써 후보 분포를 찾아내는 것 입니다.

Likelihood Function이 최대가 되는 \theta를 찾는 것은 최적화 문제로써 제약조건이나 분포의 파라미터 상황에 따라 solution이 다양하게 존재하게 됩니다.

우리의 신경망도 사실 어떻게 보면 MLE의 과정이라 볼 수 있죠. 학습 데이터라는 표본 집단을 가지고 실제 시나리오에서도 잘 동작할 수 있도록 모집단의 분포를 찾아나갈 수 있게 파라미터를 조정하는 과정이니 말이죠.

Introduction

요즘 정말 Vision-Language Model 만큼 뜨거운 연구 주제도 없는 것 같습니다. OpenAI가 만들어낸 CLIP은 4억개의 이미지 텍스트 페어를 활용하여 사전학습된 embedding space를 제공하여 정말 다양한 분야에서 활용이 가능한 표현력을 제공하고 있습니다.

CLP의 embedding space는 cross-modal retrieval, question-answering, stable-duffsion 등 다양한 분야에서 활용이 되고 있지만 나름 한계점을 가지고 있습니다.

애초에 4억개의 image-text pair가 일대일 방식으로 matching이 되어 있는데, 여기서 발생할 수 있는 문제점은 하나의 캡션이 다양한 이미지에 매칭될 수 있다는 점 입니다. 캡션이 하나의 이미지에만 들어 맞는 것은 아니기 때문에 필연적으로 CLIP의 pair는 한계점을 가지게 됩니다.

또한 CLIP의 embedding space는 deterministic 하다는 문제점이 존재합니다.

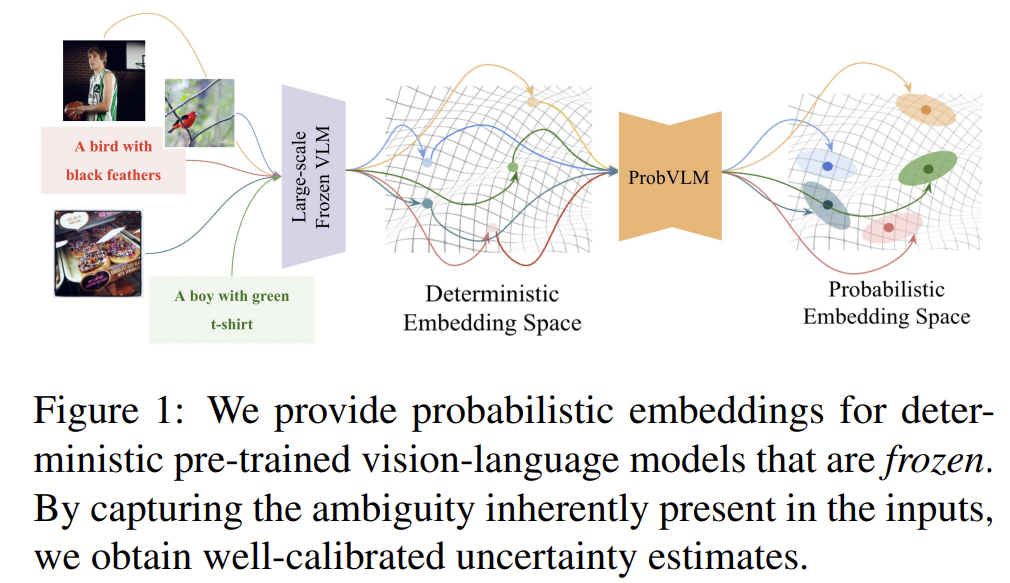
제가 리뷰 시작하기 전에 이미 deterministic과 probabilistic의 차이를 설명했으니 헷갈리시는 분들은 참고하시면 됩니다. 당연하게도 embedding space가 deterministic 하다면 이런 modal간의 ambiguity를 해결하기 어렵습니다.

여기서 얘기하는 ambiguity는 아까 얘기했던 것 처럼 하나의 캡션이 다양한 이미지에 매칭될 수 있는 상황에 대한 가능성이라 보면 될 것 같네요.

즉, 현재 CLIP의 embedding space는 하나의 single vector로 구성되고 있기 때문에 uncertainty를 modeling 할 수 없고, 저자는 이를 해결하기 위한 probabilistic embedding 방법을 제안합니다. 기존에도 이러한 probabilistic embedding을 도입하는 연구들이 있었습니다.

probabilistic embedding을 사용하는 건 좋은데 기존 연구들이 이를 위해 scratch 방식으로 학습 시켰다는 것이 저자는 문제로 지적합니다. CLIP 같은 경우는 더군다나 OpenAI와 같은 회사가 아니면 scratch로 학습하는 것이 매우 어렵기 때문에 다른 방법이 필요 합니다.

이렇게 대용량 사전 학습된 embedding space를 원하는 space로 만들기 위해 최근 연구들은 scratch 방식으로 학습 하는 것이 아니라 간단한 레이어만 추가하여 학습 하는 방식으로 진행이 되고 있습니다.

즉, 사전 학습된 인코더는 freeze 시키고 뒷단에 무언가 목적에 맞는 adapter를 붙여서 adapter만을 잘 학습 시키는 것이라 볼 수 있습니다. 여기서도 probabilistic embedding을 위해서 앞단의 encoder를 학습 하는 것이 아니라 뒷단의 adapter만을 학습 시키는 방법을 제안합니다. 이렇게 하면 좋은 것이 학습의 cost를 낮출 수도 있으면서 사전 학습된 CLIP의 representation도 이용할 수 있다는 것이죠.

그렇다면 이제 어떤 확률 분포로 모델링을 할 것이냐 가 중요한 포인트인데 그 부분에 대해서는 이제 Method 에서 살펴보도록 하겠습니다.

Method

기본적으로 사전 학습된 CLIP Encoder는 \Phi로 정의합니다. 그리고 우리는 이 CLIP Encoder는 freeze 한 상태로 사용합니다. CLIP representation 만을 사용하기 위함 입니다.

• \Phi_{\mathcal{V}}(\cdot;\theta_{\mathcal{V}}):\mathcal{I}\rightarrow \mathcal{Z}

CLIP Image Encoder 입니다. 이미지를 입력 받으면 CLIP embedding space에 위치하고 있는 vector를 내놓는 것이죠.

• \Phi_{\mathcal{T}}(\cdot;\theta_{\mathcal{T}}):\mathcal{C}\rightarrow \mathcal{Z}

CLIP Text Encoder 입니다. 이미지를 설명하는 caption을 입력 받으면 마찬가지로 CLIP embedding space에 위치하고 있는 vector를 내놓게 됩니다.

그리고 우리는 이 vector를 다시 proejction 시켜서 어떠한 확률 분포를 구성하는 parameter를 추정 합니다.

이 때 우리가 학습 하려고 하는 adpater layer를 ProbVLM이라 정의하고 \Psi라고 표기 합니다.

• \Phi_{\mathcal{V}}(\cdot;\zeta_{\mathcal{V}}):\mathcal{Z}\rightarrow \mathcal{P}

ProbVLM Image Component 입니다. CLIP Image Encoder로 나온 deterministic embedding z를 입력으로 받아 분포를 구성하는 파라미터를 출력으로 반환 합니다.

• \Phi_{\mathcal{T}}(\cdot;\zeta_{\mathcal{T}}):\mathcal{Z}\rightarrow \mathcal{P}

마찬가지로 ProbVLM Text Component 입니다. CLIP Text Encoder로 나온 deterministic embedding z를 입력으로 받아 분포를 구성하는 파라미터를 출력으로 반환 합니다.

확률 분포 모델링에 대한 어려운 얘기를 하기 전

저자는 일단 CLIP Encoder를 통해서 나온 embedding vector(z=\Phi(x;\theta))를 분포의 평균으로 사용하기로 합니다. 대용량 데이터에서 사전 학습된 representation인 만큼 high-quality의 embedding point를 제공하기 때문이죠.

이러한 가정을 바탕으로 이제 ProbVLM을 잘 학습을 시키기 위해서는 정교한 확률 분포 모델링이 필요하겠네요. 저자는 이를 위해 두 가지 학습 전략을 고안 합니다.

Estimated parameter should remain faithful to the original unimodal embedding (intra-modal alignment), this makes the uncertainty of the ProbVLM serve as a good proxy for the uncertainty of frozen encoders

우선 추정되는 파라미터가 원래 unimodal embedding과 비슷해야 한다는 것 입니다. 추정되는 파라미터가 원래의 unimodal embedding과 너무 다른 양상을 보이면 기존 pretrain encoder의 uncertainty를 측정하기 어렵다는 것 입니다.

Estimated parameters should capture the ambiguities and uncertainties present within and across modalities (cross-modal alignment)

다음으로 추정되는 파라미터가 서로 다른 modality끼리도 비슷하게 유지가 되어야 한다는 것 입니다.

그래서 우리의 목적 함수는 크게 두 가지로 구분이 됩니다. Intra-modal Objective, Inter-modal Objective 이렇게 말이죠.

이제 아래의 그림을 통해 한번 전반적인 구조를 살펴보도록 하겠습니다. 굉장히 복잡해 보이지만 개념 레벨의 이해는 어렵지 않습니다.

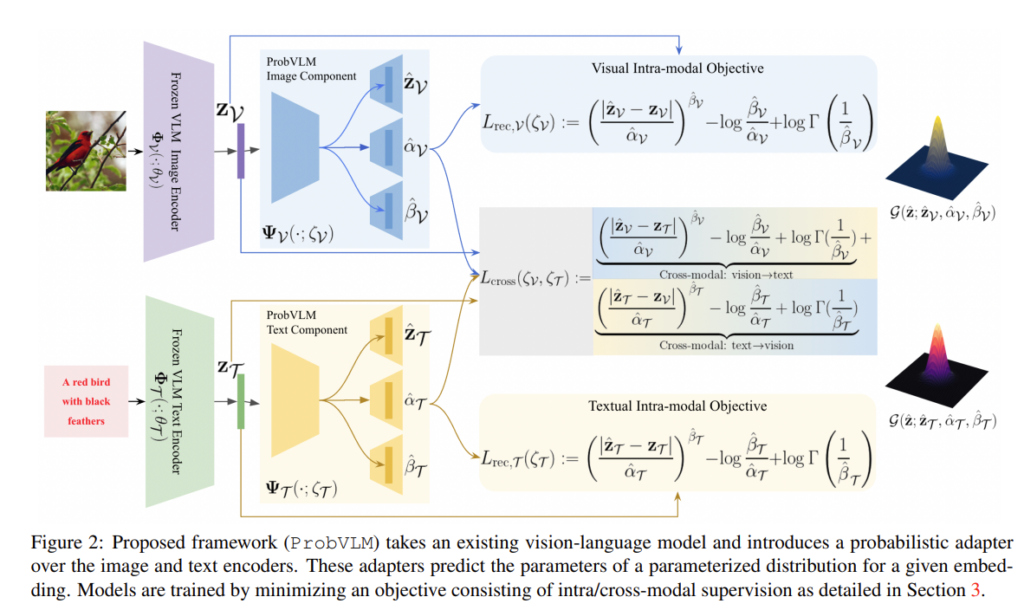
Intra-modal Alignment

동일한 modality 내에서 분포를 만들 때 전체적인 방향은 아래와 같습니다.

CLIP Image, Text Encoder를 사용하여 해당 modality에 대한 embedding vector를 다음과 같이 얻을 수 있습니다.

• z=\Phi(x;\theta)

그리고 modality-specific component는 \Psi(\cdot;\zeta)는 z를 reconstruct 하는 방식으로 학습이 되는 것 입니다. 이 때 완전히 동일하게 reconstruct 하는 것 보다 어느 정도 uncertainty를 고려하는 방식으로 진행이 됩니다. ResNet의 아이디어처럼 residual을 모델링 한다고 보시면 됩니다.

이러한 상황에서 저자는 확률 분포를 모델링 하려고 할 때 다음 두 가지 사항을 고려한다고 합니다.

• I.I.D constraints를 조금 relax하여 모델링 합니다. independent한 분포를 각각 생성하지만 indentical한 분포는 고려하지 않는 방식으로 말이죠. 생각해보면 모든 데이터가 독립적인 분포를 가지는 것은 자연스럽지만 동일한 분포를 따르는 것은 어려울 것 같기도 하고 그래야만 할 필요도 딱히 없어 보이기 때문 입니다.

• residual에 대한 heteroscedasticity를 heavy-tailed distribution을 따르도록 학습 시키는 것. 사실 여기는 저의 기반 지식이 부족하여 설명을 제대로 할 수 없을 것 같아 그냥 그런가 보다 하고 넘어가겠습니다.

저자는 위의 설계 방식을 만족 시키기 위해 확률 분포를 Generalized Gaussian Distribution (GGD)로 가정 합니다.

GGD가 저자가 모델링 하려는 heavy-tailed distribution을 모델링 할 수 있어 선택한 것 같습니다. GGD를 특정하기 위해서는 세가지 파라미터를 추정해야 합니다. \mu, \alpha, \Beta 입니다. 각각, mean, scale, shape에 대한 파라미터 입니다.

그리고 우리는 결국 최대 우도법(MLE)에 따라

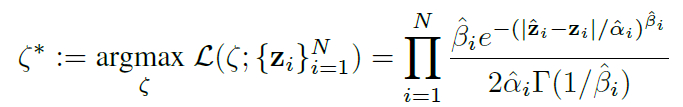
Likelihood function을 최대로 하는 파라미터 \zeta^{*}를 찾아야 합니다.

보통 최대 우도법을 전개할 때는 Log를 취해서 곱하기 연산이 아니라 더하기 연산으로 바꿔주고 음의 값을 곱해서 최소화 문제로 변환해서 풀곤 합니다. 여기서도 음의 Log를 취해서 위의 최적화 문제를 아래처럼 변환을 해주게 됩니다.

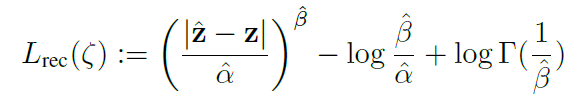
위의 식이 아래의 식으로 정리된 것은 간단한 식 조작이니 직접 로그를 취해서 곱하기 연산을 전개하면 됩니다.

ProbVLM의 Vision Component, Text Component 모두 위의 L_{rec}(\zeta) 손실 함수를 통해 최적화가 진행 됩니다.

Cross-modal Alignment

다음은 서로 다른 modality 간의 분포가 비슷하게 형성 될 수 있도록 하는 부분 입니다. 예를 들어 서로 같은 쌍의 이미지와 텍스트 같은 경우는 각각의 확률 분포가 제각각인 것 보다는 어느 정도 분포가 비슷하게 나와야 한다는 것이죠. 그래야 cross embedding distribution이 제대로 작동을 할 것이니 말입니다.

여기서 등장하는 다양한 수학적 이론 배경이 저도 너무 어려워서 자세한 설명은 어려울 것 같고 해당 Cross-modal Alignment 모듈의 목적 자체만 기억을 해두시면 될 것 같습니다.

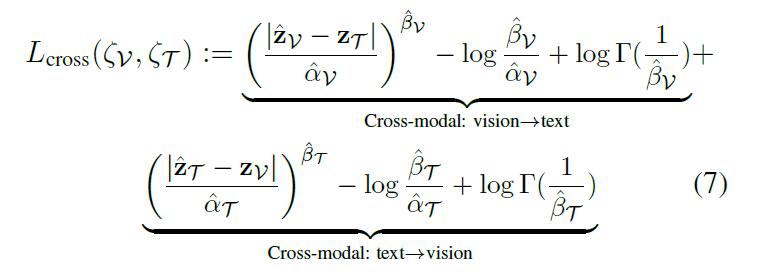
결론적으로는 (7)의 수식을 통해서 Cross Modal Alignment를 수행할 수 있었습니다. (7) 수식의 유도가 궁금하신 분들은 논문을 직접 찾아보시는 것을 추천 드리지만 Bivariate Fox H-function이라는 난해한 개념에 대한 이해가 필요하니 참고하시길 바랍니다.

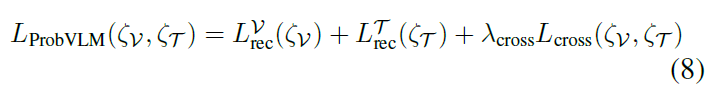
최종 Loss는 위의 수식처럼 Intra와 Cross에서 발생하는 Loss를 더한 형태로 사용해주고 있습니다.

Experiments and Results

Datasets, Metrics

데이터 셋은 COCO, Flicker-30k, CUB를 사용하여 cross-modal retrieval을 평가하였고, Oxford-Flowers 102를 사용하여 좀 더 fine-grained 상황에서 cross-modal retrieval을 평가하였다고 합니다.

Image-to-Text Retrival 혹은 Text-to-Image Retrieval에서는 Recall@K metric을 사용하여 정량적 평가를 진행하였습니다.

추가적으로 추정된 uncertainty에 대한 calibration 평가를 위해서 uncertainty level을 정의하고 Spearman rank correlation (S라 표기)를 사용하여 uncertainty level과 Recall@k retrieval 사이의 calibration 정도를 측정한다고 합니다. (무슨 말인지는 잘 모르겠네요..)

이상적인 모델이라면 uncertainty가 증가하면 성능이 단조적으로 떨어지는 것이 정상이라고 하네요.

이를 위해 uncertainty level과 R@1 사이의 회귀 정도(R^{2})를 측정한다고 합니다. 성능 하락 정도가 선형적인지를 보기 위함이라고 하네요.

마지막으로 두 score의 내적(S, latex]R^{2}[/latex])을 측정하여 -SR^{2}를 측정한다고 합니다. 1의 값을 가진다면 이상적인 모델이라고 하네요.

Calibrated Uncertainty via ProbVLM

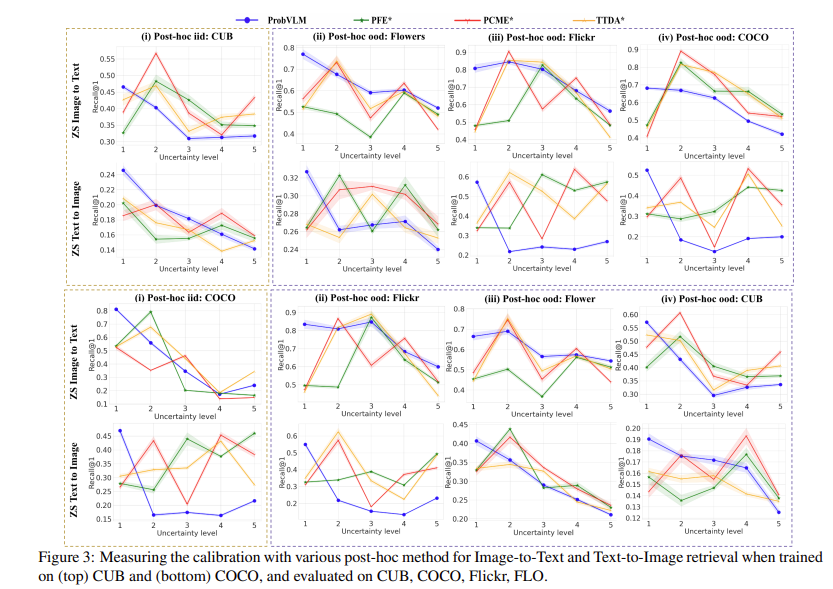
우선 아래의 그래프를 보시면 Uncertainty level과 R@1 사이의 관계를 보여주고 있습니다. 비교 방법 베이스라인들은 PFE, PCEM, TTDA라는 방법론들 입니다.

전체적으로 저자가 제안하는 ProbVLM 같은 경우 Uncertainty level이 증가하면 성능도 monotonically 하게 감소하고 있지만 다른 방법들은 설명할 수 없는 양상을 보여줍니다. 이는 해당 방법들이 Uncertainty에 대한 고려가 되어 있지 않기 때문에 나타나는 결과라고 해석할 수 있을 것 같네요.

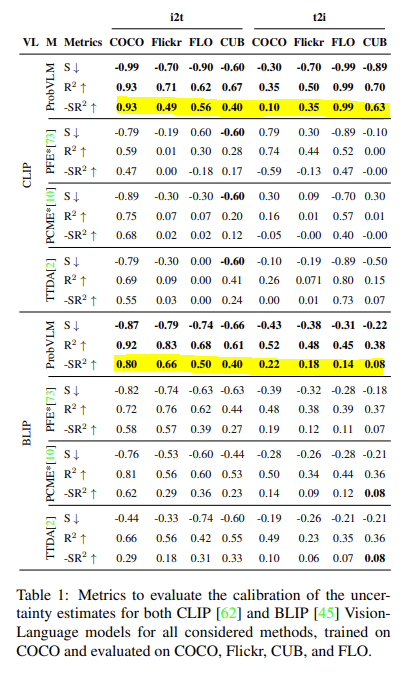
아래의 테이블은 4가지 데이터 셋에 대해서 Cross-modal Retrieval 정량적 지표 입니다. 해석이 어려워서 SR^{2} 위주로 보겠습니다.

우선 ProbVLM이 SR^{2} 기준 타 방법론들보다 모든 데이터 셋에서 가장 좋은 성능을 보여주고 있습니다.심지어 t2i 상황에서 FLO 데이터 셋에서는 거의 완벽한 수준(0.99)을 보여주고 있습니다. 이는 CLIP과 BLIP 모두 동일한 경향성을 보여주고 있습니다.

이를 통해 ProbVLM은 타 방법론 대비 uncertainty가 가장 잘 고려된 방법이라 정리할 수 있을 것 같습니다.

다음은 Deterministic한 embedding과의 차이를 보여주는 정성적 결과 입니다.

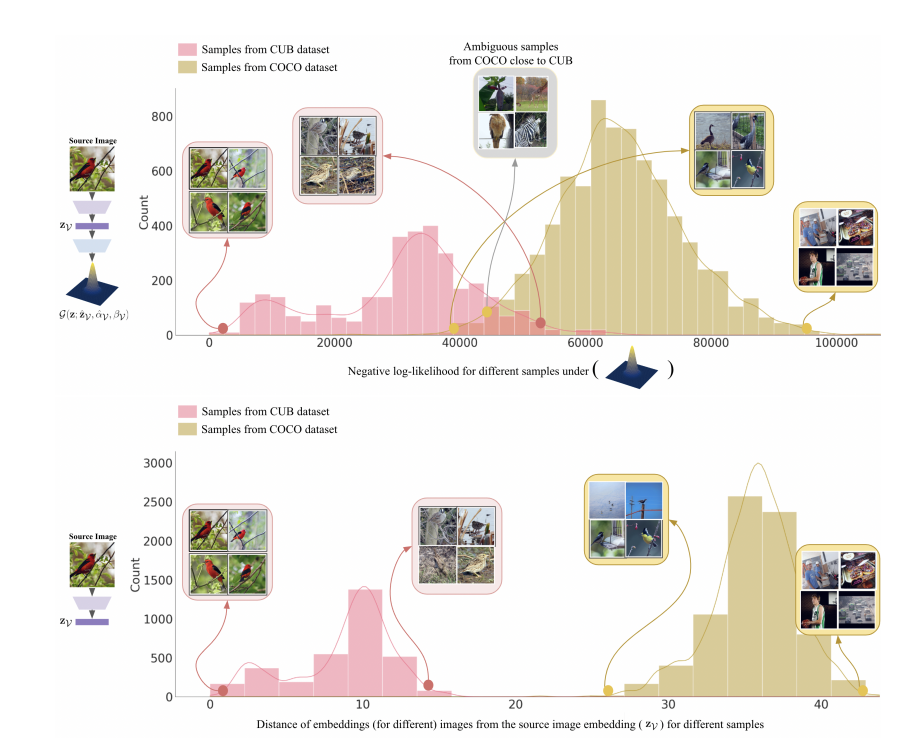
상단의 분포를 보면 COCO dataset과 CUB dataset에서 모델이 헷갈려 하는 샘플을 시각화해서 나타내고 있습니다. 흥미로운 것은 서로 다른 데이터 셋 이지만 모델이 헷갈려 하는 샘플들이 비슷하게 bird라는 것이 확인된다는 것 입니다. 분포가 겹치고 있죠? Probabilistic Embedding을 통해 이러한 model의 ambiguity를 고려하였기 때문에 나타난 결과라 볼 수 있습니다.

하지만 반대로 하단의 분포를 보면 Deterministic한 상황에서는 서로 다른 데이터라면 확연하게 분리가 되고 있습니다. Bird라는 샘플을 헷갈려하는 것은 동일한데 임베딩이 다르게 표현된다는 것이죠.

Applications

저자가 모델링한 Uncertainty는 다양한 응용이 가능하다고 합니다. 1) Active Learning이고 2) Model Selection 이죠.

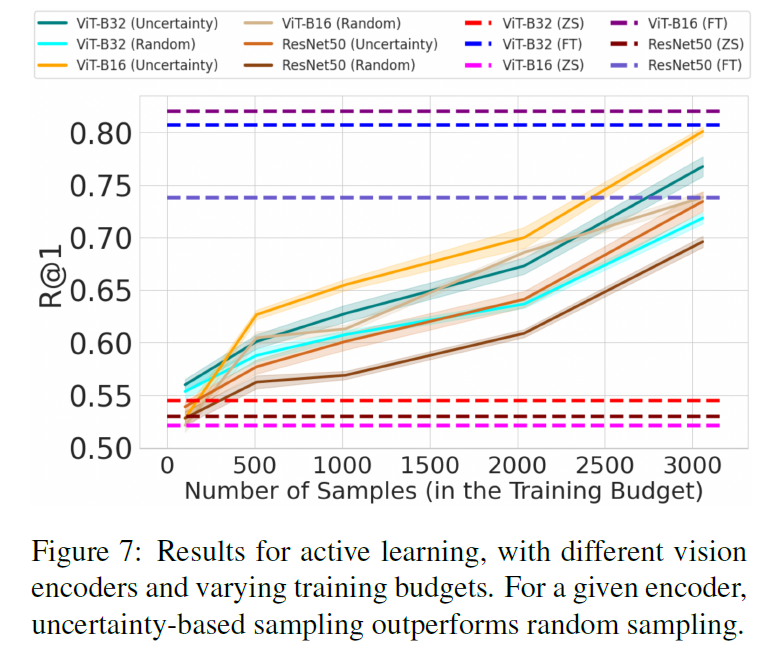
실험 세팅이 궁금하신 분은 논문을 직접 읽어보시고, 결과를 놓고 보면 저자가 제안하는 Uncertainty 기반으로 Sampling을 진행하면 다양한 Backbone에서 Random Sampling 한 것보다 더 좋은 성능을 보여주고 있습니다.

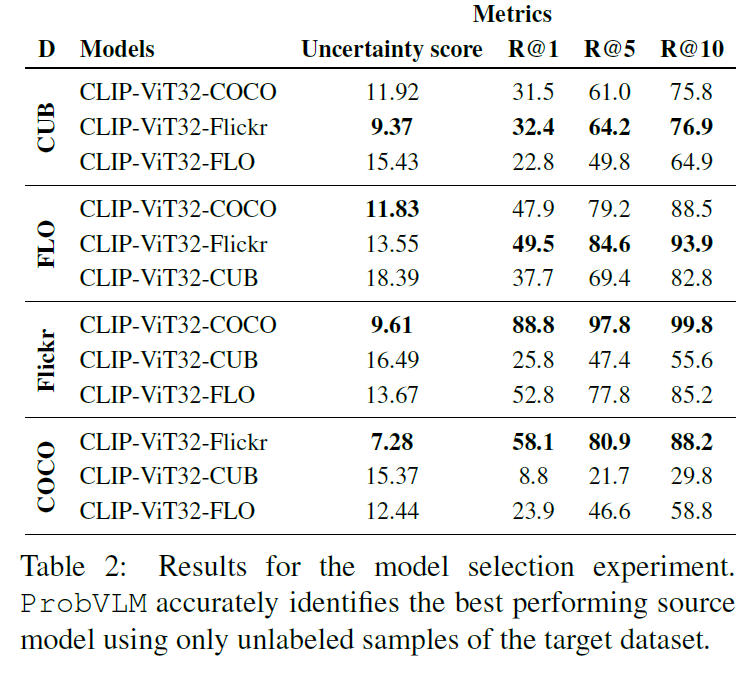
Model Selection 관점에서도 Uncertainty가 낮은 Model을 선택하면 down stream task에서 더 좋은 성능을 보여주는 것은 세가지 데이터 셋에서 보여주고 있습니다.

Latent Diffusion for Embedding Uncertainty

마지막으로 Stable Diffusion을 이용하여 얻어진 분포에 대해서 해석을 진행하고 있습니다. 굉장히 흥미롭네요.

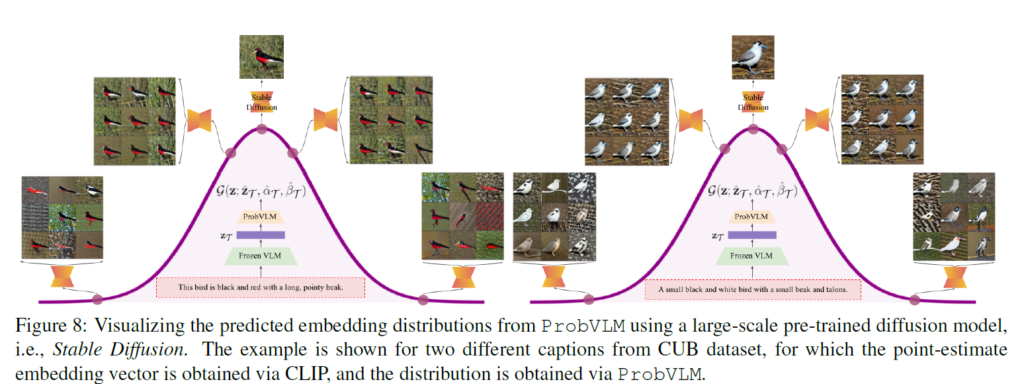
얻어진 분포에서 sampling 하여 임의의 vector를 생성하고 이를 사전 학습된 Diffusion Model을 사용하면 해당 vector에 대한 이미지를 생성할 수 있습니다.

보시면 평균 근처에서 샘플링한 vector로 생성된 이미지는 원래 CLIP 이미지와 유사하게 나오는 반면 평균에서 멀어질 수록 다양한 sample 들이 관측이 되고 있습니다. 하나의 caption이 다양한 이미지에 대응할 수 있는 potential이 생겼다고 볼 수 있습니다.

Multimodal 연구와 Diffusion 연구가 합쳐지면 이러한 해석도 가능하다는 것이 정말 흥미롭습니다.

Conclusion

요즘 확률적 임베딩에 저희 팀이 관심을 가지고 있는데 참고할만한 좋은 논문을 하나 읽게 된 것 같습니다.

그런데 대용량 데이터로 사전 학습된 representation 자체를 분포의 평균으로 가져간다는 접근은 저희 실험에서도 고려할만한 접근인 것 같습니다.

코드도 공개가 되어 있어서 논문에서 제안하는 Loss를 뜯어볼 수도 있어 괜찮은 것 같습니다.

아쉬운 것은 저희 수리적 배경이 깊지 않다 보니 분포를 모델링하는 과정에서의 insight를 충분히 이해하지 못한 것이 있네요.

리뷰 읽어주셔서 감사합니다.