이번에 소개드릴 논문은 ICCV2023에 게재된 Self-supervised monocular depth estimation 관련 논문으로, monocular depth estimation이라는 task에 초점을 맞춘 모듈을 새롭게 제안함으로써 성능을 향상시키고자 한 논문입니다.
Intro
단안 영상 깊이 추정이라는 task는 multi-view image를 통해서 깊이를 추정하는 것과 비교하여 상당히 어려운 task에 속하게 됩니다. 이는 하나의 영상에서 각 객체의 픽셀들에 대한 깊이를 추정해야 하지만, 오브젝트의 픽셀들 하나하나들이 깊이를 추정하는데 있어서 충분한 정보를 가지지는 못하기 때문이죠.
결과적으로 단안 영상으로부터 깊이를 잘 추정하기 위해서는 깊이 추정 모델이 객체와 주변 환경 사이에 관계에 대하여 제대로 이해해야 한다고 볼 수 있습니다. 이러한 객체와 주변 환경 사이에 대한 관계가 정확히 무엇인지에 대하여 보다 자세히 알아보기 위해 저자는 간단한 실험들을 진행합니다.
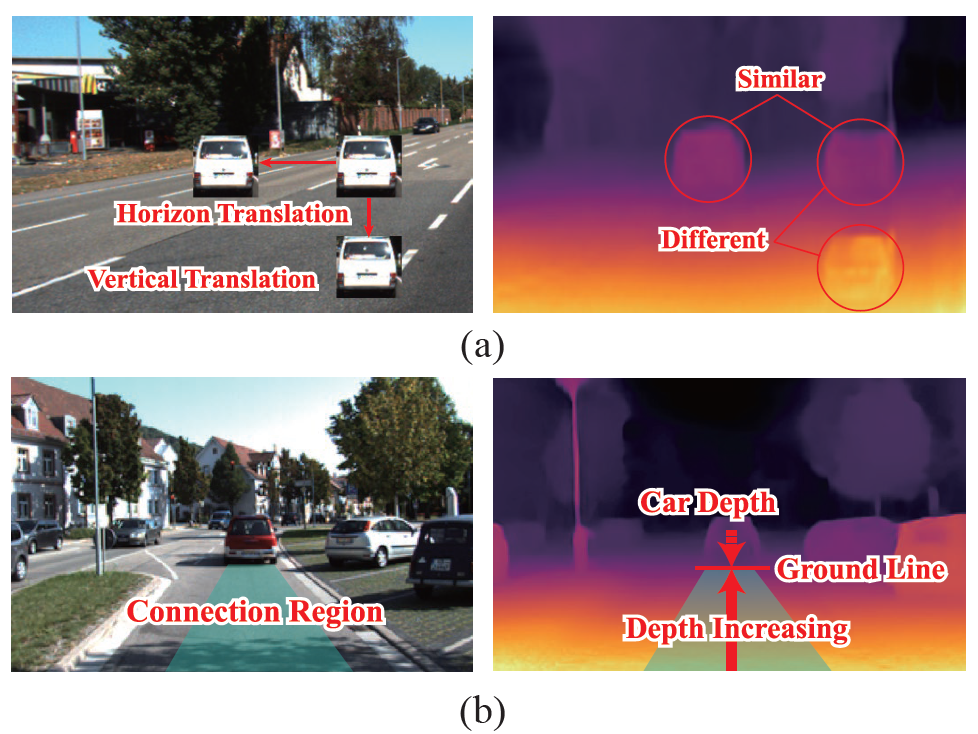
그림1-(a)는 하나의 장면에 대해서 crop한 자동차 사진을 주변 영역에 대해 붙인 이미지를 보여주고 있습니다. 여기서 재밌는 점은 동일한 자동차의 사진임에도 불구하고, 영상의 어느 위치에 존재하느냐에 따라서 추정된 깊이의 결과값이 상이하다는 것을 확인하실 수 있습니다.(그림1-(a) 우측의 마그마 색상 그림 참조)
저자들은 이러한 관측을 토대로, 깊이 추정에서 방향이라는 정보가 깊이 추정에 큰 영향을 주는 것이 아닌가 추측합니다. 즉 수직에 해당하는 라인은 depth의 variation을 나타내는 경향성이 크며, 수평에 해당하는 라인은 depth의 consistency를 유지하는 것이죠.
이러한 방향성에 따라서 추정되는 깊이의 결과값이 달라지는 것에 대하여, 그렇다면 어떠한 방향성(수직 or 수평)이 깊이 추정 성능에 큰 영향을 끼치는가에 대해 분석하고자 저자는 한가지 간단한 실험을 진행합니다. 바로 monodepth2라는 가장 기본적인 모델에 대하여 입력으로 들어가는 해상도를 수직과 수평에 따라 다양하게 넣어보는 것이죠.
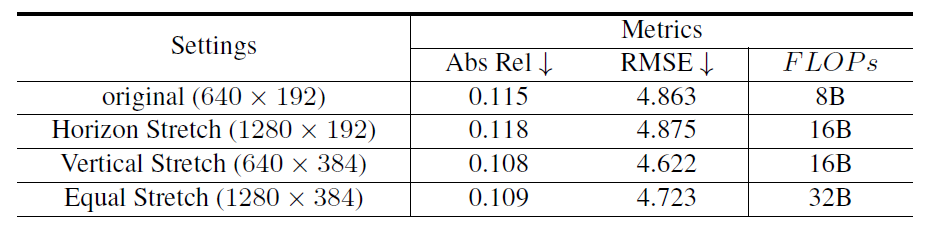
위에 표의 setting 열을 살펴보시면 original부터 equal stretch까지 4가지의 실험 세팅이 있는 것을 확인하실 수 있습니다. 여기서 original의 경우에는 가장 기본적인 세팅인 Width 640, Height 192의 해상도를 지닌 영상을 입력으로 모델을 학습 및 평가한 것이죠.
여기서 Horizon stretch와 Vertical Stretch는 각각 너비와 높이를 2배씩 upsampling하여 모델을 학습 및 평가를 한 것을 의미합니다. 실제 결과를 살펴보면, Horizon Stretch의 경우에는 모델의 성능이 두가지 평가 메트릭에서 모두 성능이 하락한 것을 확인하실 수 있는 반면에 vertical stretch의 경우에는 상당히 큰 성능 향상을 볼 수 있습니다.
일반적으로 monocular depth estimation의 경우에는 입력 해상도를 크게 할 수록 더 좋은 성능을 달성한다고 보여지며 실제 위에 표에서도 original setting보다는 모든 해상도를 2배씩 키운 Equal Stretch가 Abs Rel과 RMSE 평가 메트릭이 모두 좋은 것을 확인하실 수 있습니다.
하지만 이전 연구들에서는 해상도가 커지면 보다 디테일한 정보들을 볼 수 있기에 정확한 깊이 추정을 가능하다고 생각을 했지 방향성에 대해서는 크게 고려하지 않은 것이 현실이었습니다. 이러한 관점에서 저자가 위에 실험에서 밝혀낸 결과들은, 단순히 해상도 증가가 아닌, vertical 성분들의 해상도가 커지는 것이 중요하다라는 것을 간접적으로 밝혀낸 것이죠.
그리고 저자들은 보다 구체적으로, 영상 내 Connection Region이라는 부분이 깊이를 추정하는데 있어 매우 중요하다라고 주장하고 있습니다. 여기서 Connection Region이란 그림1-(b)에서 푸른색으로 색칠된 영역을 참고하시면 되는데, 보다 자세하게는 카메라로부터 어떠한 객체 사이까지의 영역이라고 생각하시면 편합니다. 즉 그림1-(b)의 예시에서는 영상의 맨 아래 픽셀부터 자동차 하단부까지의 연결된 픽셀을 의미하는 것이죠.
그러면 이 논문의 목표는 이제 정해졌습니다. 어떻게 하면 vertical 성분들에 대해서 모델이 더 잘 특징을 추출하고 이해하여 보다 정확한 깊이를 추정할 수 있을까?로 접근하면 되는 것이죠.
일단 저자는 일반적인 CNN의 경우에는 이러한 방향성에 대하여 feature를 잘 이해하고 추출하기 어렵다고 주장합니다. 이는 CNN의 고질적인 문제점이었던 작은 receptive field(그리고 하나의 feature map에 연산을 할 때 항상 일정한 receptive field를 가진다는 점)으로 인하여, 인코딩되는 정보들이 유사하다는 특징이 큰 문제라고 지적합니다.
게다가 convolution 연산은 center position에 중첩되어 정보를 aggregation하는 것이기 때문에, connection region을 encoding하는 것이 쉽지 않다고 합니다.
따라서 저자들은 이러한 문제를 해결하기 위해, Direction-aware Cumulative Convolution Network(DaCCN)이라는 방법론을 새롭게 제안합니다. DaCCN은 크게 2가지 contribution을 가지고 있는데, 하나는 learnable affinity transformation module을 통해서 모델이 direction-aware하게 feature를 추출할 수 있도록 하는 것이며, 다른 하나는 DaCCN이 connection region으로부터 환경적인 정보를 효율적으로 취합할 수 있도록 하는 누적합 기반의 연산 모듈을 새롭게 적용한 것입니다.
보다 자세한 내용은 아래 method에서 다뤄보도록 하죠.
Method
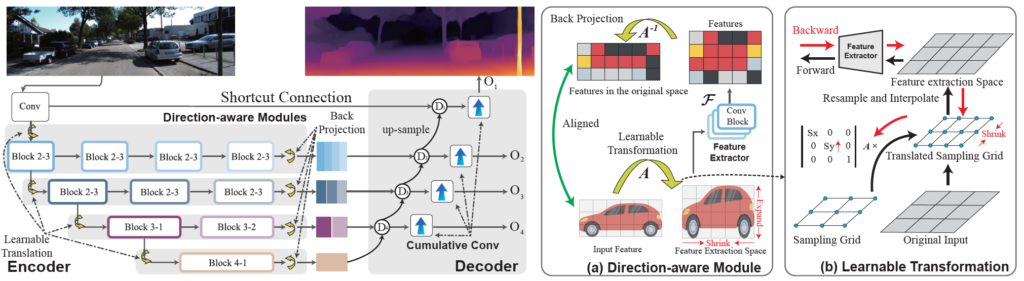
그림 2는 저자가 제안하는 모델의 전체 pipeline으로 보시면 됩니다. 좌측의 Depth model을 살펴보시면 Encoder가 저희가 아는 모습과는 조금 다르게 생긴 것을 확인하실 수 있습니다. 모든 해상도에 대해서 conv block이 끝까지 지속되어 모든 해상도의 feature map을 추출하는 것을 볼 수 있죠.
이는 BMVC2022에 게재된 DiFFNet이라고 하는 방법론을 baseline으로 삼았기 때문에 해당 모델의 구조를 그대로 모방한 것으로 이해하시면 됩니다. DiFFNet의 경우에는 HRNet을 backbone model로 활용하였으며 이 HRNet이 기존의 ResNet등과 같은 모델과 다르게 모든 해상도의 feature map을 계속해서 컨볼루션에 태워 연산을 이어가는 나름 재밌는 구조를 가진다고 말씀드리고 싶습니다.
아무튼 저자들의 첫번째 contribution인 Direction-aware Module (feat, Learnable Transformation)은 Encoder의 각 stage 별로 구성된 Block n-m 내부에 존재하게 됩니다.
그리고 두번째 contribution인 Cumulative Conv의 경우에는 Decoder 단계에서 깊이 map을 추정하기 바로 직전에 연산되는 과정으로 이해하시면 되고 각각의 contribution에 대한 보다 자세한 내용을 지금부터 다루기로 하죠.
Direction-aware feature extraction
가장 첫번째로 Direction-aware feature module에 대한 설명입니다. 일반적으로 semantic segmentation, classification과 같은 task들은 feature map 내에 방향에 대한 정보들이 모두 비슷한 중요도와 결을 가지게 됩니다. 하지만 intro에서도 살펴보셨다시피, depth estimation에서는 vertical 방향쪽 성분들이 깊이를 결정하는데 상당히 중요한 역할을 수행하게 됩니다.
따라서 저자는 각 방향으로부터 특징을 추출하는 것을 추가로 배울 수 있는 direction-aware module이라는 것을 새롭게 제안합니다. 일단 저자들은 Encoder의 특징 추출 과정에서 sample density와 receptive field가 방향과 관련된 특징 추출에 중요한 요소라고 판단을 하였습니다.
Receptive field는 다 아시는 내용이니 넘어가고, sample density에 대해서 저자는 입력 영상의 한 영역으로부터 추출된 특징 벡터의 개수라고 정의를 하였는데, 이에 대한 설명이 조금 분명하지는 않습니다. 하지만 제가 생각하였을 때는 feature map의 해상도와 조금 연관성이 있어보이네요. 즉 하나의 대상을 표현할 때 더 많은 픽셀로 표현하게 되면 해당 대상을 보다 선명하고 디테일하게 나타낼 수 있다는 것이죠.
이러한 관점에서, 저자는 더 세부적인 정보를 포착하기 위해서는 작은 receptive field를 가지고 대신에 feature map의 density는 커야만 하며, 반대로 global information을 포착하기 위해서는 큰 receptive field를 가지고 대신에 feature map의 density는 작아야한다고 합니다.
사실 이 내용은 당연할 수 밖에 없죠. receptive field를 키운다는 것은 한번에 연산해야하는 feature map의 pixel들이 많다는 것인데, 이때 feature map의 density마저 크게 되버리면 연산량이 매우 커지기 때문에 실용적이지 못하게 됩니다.
아무튼 다시 본론으로 들어와서, 저자는 이러한 기존 인코더들의 구조와 결이 맞게끔 direction-aware module을 설계하고자 하였다고 합니다. 결론부터 말씀드리면 저자가 위에서 설명한 의도가 direction-aware module 내부 설계에는 반영이 된 것으로 저는 보지 않습니다만, direction-aware module을 encoder의 모든 block stage에 적용했다는 것이 위의 관점들을 반영했다라고 볼 수 있어서 저자는 그렇게 주장하는 것 같습니다.
그러면 direction-aware module 내부에 대해서 자세히 알아보도록 하죠. Direction-aware Module은 크게 3가지 파트로 구성이 되어있습니다. 바로 affinity transformation A, convolution feature extraction block \mathcal{F} 그리고 back projection transformation A^{-1}가 되겠습니다.
그림2-(a), (b)를 살펴보시면 대략적인 파이프라인을 살펴보실 수 있는데, 쉽게 요약하면 다음과 같습니다.
Learnable Affinity transformation을 입력 feature map에게 적용한 다음에, 컨볼루션 연산을 적용하여 feature encoding 과정을 수행합니다. 그 다음에 처음에 적용했던 affinity transformation의 역행렬을 적용해서 다시 원래대로 돌리는 것을 의미하죠. 수식적으로 표현하면 아래와 같습니다.
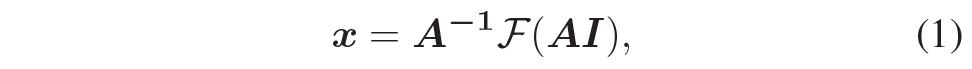
그렇다면 왜 이런식으로 설계를 했을까요? 이러한 컨셉의 이해는 16년에 나온 제법 옛날 논문인 Spatial transformation network을 아시면 쉽게 이해하실 수 있을 것으로 생각합니다. 이 STN의 목표는 “CNN을 통해 이미지 분류를 할 때, 특정 부분을 떼어내서 집중적으로 학습시키는 것” 으로, 실제 모델 내부의 feature encoding 과정에서 이미지의 특정 부분을 affine transformation하는 재밌는 방법론이었습니다.
마찬가지로, 본 논문의 경우에도 Affine transformation을 feature map 전체에 적용함으로써 feature map 수직 혹은 수평 방향으로 변형이 될텐데 만약 수직 성분들이 길게 늘어나는 방향으로 feature map이 변형되고 해당 feature map에 대해 컨볼루션 연산을 적용하게 되면 마치 원본 해상도의 height를 stretch한 듯한 효과를 볼 수 있겠죠.
즉 컨볼루션 연산에 들어가는 입력 자체가 어떠한 learnable paramter를 통해 깊이 추정이 잘 되도록 조정이 된 상태에서 컨볼루션 연산을 수행함으로써 direction-aware한 특징 추출을 할 수 있다는 점입니다.
그러면 아까 vertical 성분들이 중요하다고 했으니 그냥 vertical 성분들에 대해서 feature map을 stretech 하는 rule-based transformation을 하면 안되냐라고 생각을 하실 수도 있지만, 사실 그렇게 단순하게 접근하는 방식은 조금 위험하기 때문에 저자들도 이를 의식하고 아래와 같이 학습 가능한 파라미터로 구성된 transformation을 설계 하였다고 합니다.
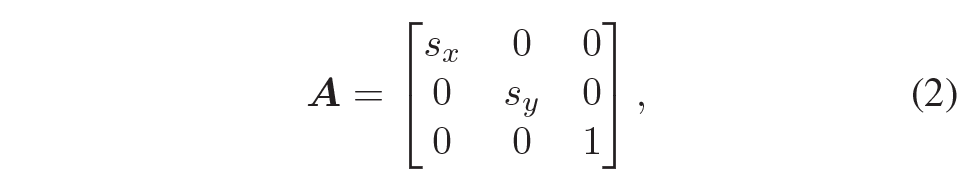
이러한 Affinity matrix를 적용하였다가 다시 inverse transformation을 수행하여 원본으로 돌림으로써 feature map의 shape 자체는 원래의 입력 영상과 동일한 shape을 지니도록 하돼, 특징을 추출하는 단계에서만 유리한 성분을 가지도록 접근하는 것이라고 이해하시면 될 것 같습니다.
Cumulative Convolution
다음은 두번째 contribution인 Cumulative Convolution에 대한 설명입니다. 해당 Convolution의 경우에는 Decoding 과정에서 적용이 되는 방식인데 컨셉이 매우 간단합니다.
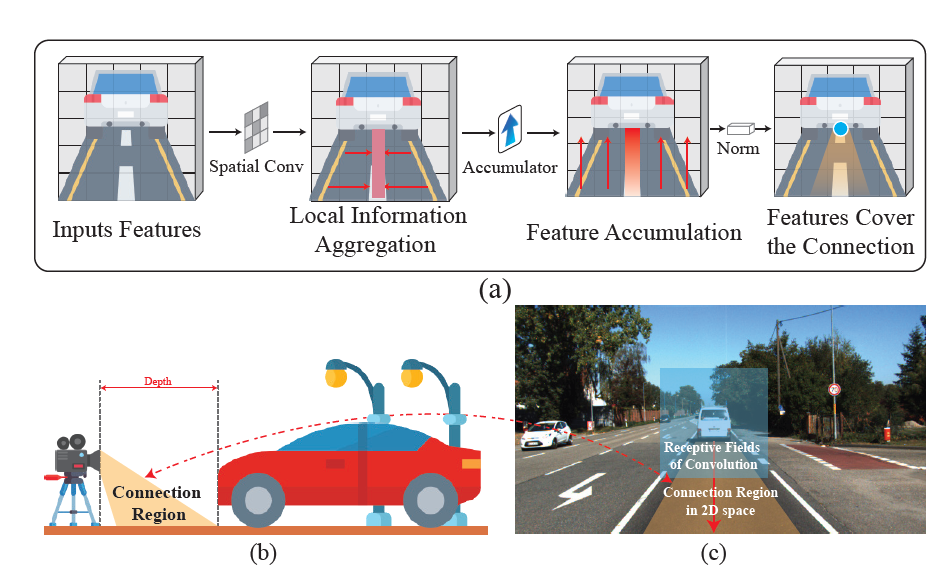
그림3은 cumulative convolution의 전반적인 컨셉과 파이프라인을 나타낸 그림입니다. 보시면 connection region에 해당하는 정보들을 어떻게 잘 aggregation 할 것이냐가 해당 컨볼루션의 핵심이다 라고 이해하시면 됩니다.
보다 자세히, connection region은 영상의 하단 제일 밑 부분에서 시작해서 object까지의 영역이라고 정의할 때, 저 부분들에 대한 정보를 어떻게 잘 취합할 것인가인데, 그림3-(c)를 살펴보시면 기존의 Convolution의 경우에는 정사각형의 receptive field를 가지고 있으며, 컨볼루션 연산 특성상 주변 이웃 픽셀들의 정보를 취합해서 필터의 센터점에 저장하는 방식으로 동작하게 됩니다.
이러한 기존 컨볼루션의 방식은 vertical 축을 따라 아래에서 위로 쭉 올라가면서 깊이에 대한 중요한 cue를 제공하는 connection region 내 정보들을 잘 취합할 수 없다는 문제가 발생하죠. 그렇다면 connection region 정보를 잘 취합하기 위해 단순히 receptive field를 높이면 되는 것 아니냐? 라는 관점으로 접근을 할 수도 있겠지만, 저자는 그러한 방식 대신 방향에 따라서 특징들을 통합하는 방향으로 설계를 하였다고 함.
저자의 cumulative convolution의 작동 방식은 그림3-(a)를 통해 확인이 가능합니다. 가장 먼저 depth-wise convolution을 통해 영상의 spatial information을 잘 다듬은 후, 단순히 맨 아래픽셀부터 현재 위치의 픽셀까지 특징들을 누적합하는 연산을 적용했다고 하네요.
근데 이제 맨 아래서부터 현재 픽셀까지의 누적합을 수행하다보면 vertical position이 위로 올라가면 올라갈수록 pixel 값 사이에 scale imbalance 문제가 크게 발생하게 됩니다. 따라서 저자는 이러한 누적합에 맞추어 새로운 정규화를 해주었는데, 이는 수식 5와 같습니다.
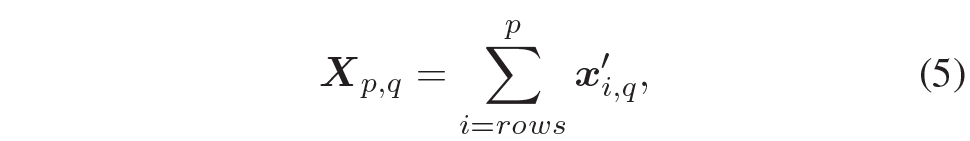
p와 q는 각각 행과 열을 의미하며 x'_{i,q} 는 i번째 행과 q번째 열의 특징을 의미한다고 합니다. 그러고나서 아래 수식과 같이 몇번째 위치의 행인지 그 값을 나눠줌으로써 최종적인 정규화가 수행이 됩니다.
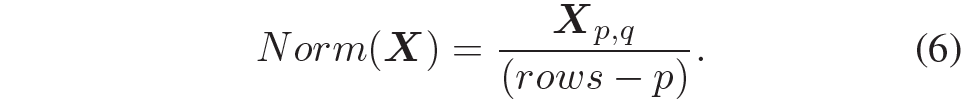
결과적으로 CumulativeConv의 과정을 수식으로 표현하면 다음과 같이 나타낼 수 있습니다.
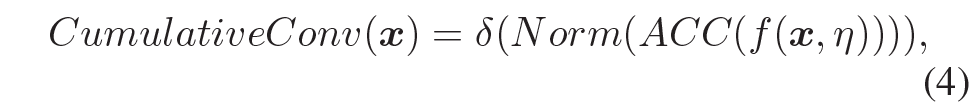
x는 input feature map, ACC는 누적합 연산, Norm은 수식6의 정규화, \delta 는 activation function을 의미합니다.
Loss function의 경우에는 기존의 Self-supervised monocular depth estimation 방법론들과 모두 동일한 loss를 사용하기에 설명을 생략하겠습니다. loss function에 대한 설명을 자세히 알고 싶으신 분들은 저나 한대찬 연구원의 예전 리뷰를 참고해주세요.
Experiments
그럼 실험 결과에 대해서 살펴보겠습니다.
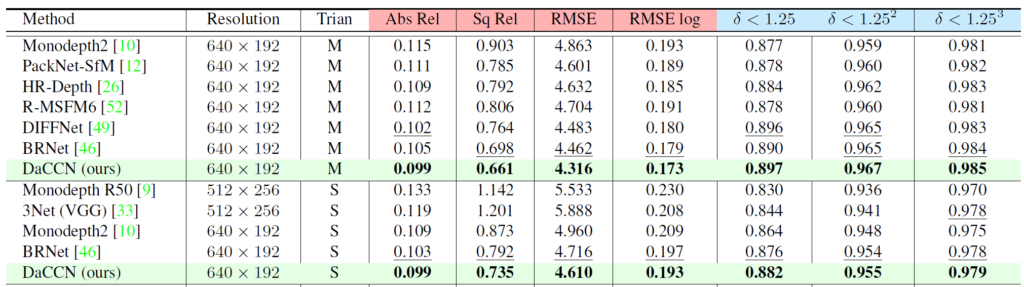
위에 테이블은 KITTI 데이터 셋에서의 정량적 비교 결과입니다. Train 열에 M과 S는 각각 Monocular video와 Stereo image를 의미하며, 이는 학습 과정에서 3개의 frame으로 구성된 monocular video를 사용한 것인지 혹은 stereo image를 활용한 것이지에 대한 내용입니다.
일단 DIFFNet이 베이스라인인데 이러한 베이스라인 대비 모든 metric에서 성능 향상이 있다는 것을 확인할 수 있습니다. 근데 한가지 의아한 점은 Stereo image로 학습하는 S setting이 더 좋은 성능을 달성하는게 일반적인데.. 여기서는 희한하게도 monocular video로 학습한 세팅이 더 좋은 성능을 달성한 것을 볼 수 있습니다.
이에 대해서 저자가 따로 언급한 것은 없는데 무언가 vertical 개념을 너무 고려했기 때문에 loss function 계산에 사용되는 stereo image는 horizon의 성질이 더 강해서 성능 개선이 줄어들었나..?라는 생각이 들기도 하고 잘 모르겠네요 이부분은.
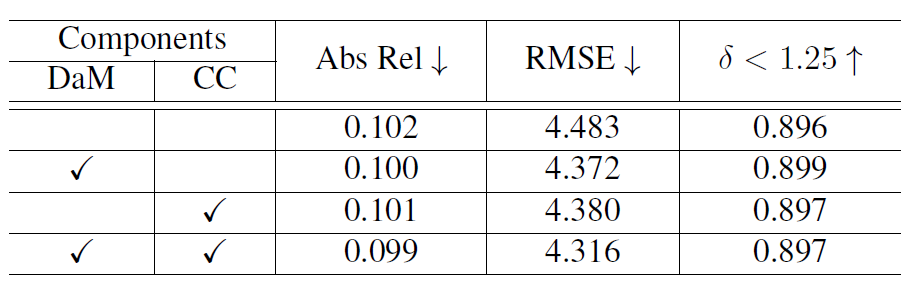
다음은 Ablation study입니다. DaM은 Direction-aware Module을, CC는 Cumulative Convolution을 의미하는데, 일단 각각의 성분들이 모두 베이스라인의 성능 향상을 일으키고 있다라는 점이 있겠으며, 이 둘을 모두 동시에 활용할 경우에 성능 향상이 크더라 라는 것을 볼 수 있습니다. (근데 delta metric의 경우에는 DaM만 적용하는 것이 더 좋게 나오긴 했네요.)
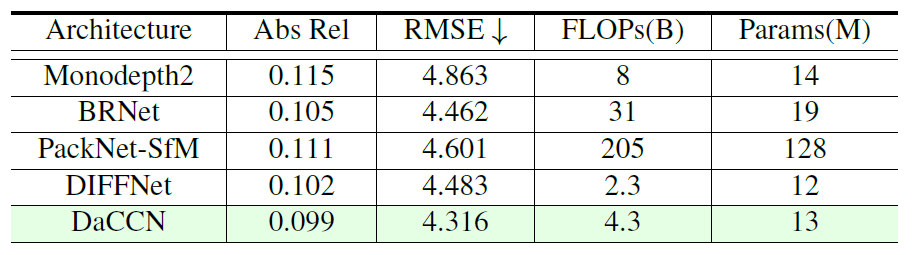
다음은 Efficiency에 대한 내용입니다. 결국 자신들의 방법론이 baseline인 DIFFNE에서 새로운 모듈들을 추가하다보니 모델 학습에 필요한 메모리나 속도가 어떤가에 대한 내용인데, 결국 learnable parameter 수도 그리 크지 않고, FLOP도 2정도 오른 수치지만 타 방법론들과 비교해서 별 차이가 안난다 라는 식으로 주장하는 것 같습니다.
근데 저 표가 좀 의심스러운 것이 제가 알기로 Monodepth2가 매우 가볍고 추론속도도 매우 빠른 것으로 알고 있는데, DIFFNET은 아무래도 backbone이 HRNet이다보니 다양한 해상도에서 많은 연산을 하게되어 추론속도가 매우 느린 것으로 알고 있습니다.
그래서 아무리 모델이 가벼워도 추론속도가 느려서 FLOP 자체가 Monodepth2보다 훨씬 커야 할 것 같은데, 여기서는 monodepth2보다 4배나 더 작다는 식으로 리포팅이 되어 있어서.. 이 부분은 신뢰하기 좀 어려울 것 같습니다. Monodepth2의 추론속도가 3090기준으로 100FPS넘게 나왔던 것이 비해 DIFFNet은 추론속도가 30FPS도 안나왔었는데 흠.. FLOPs이 어떻게 저렇게 나올 수 있는지 음…
결론
컨셉 자체가 매우 재밌었던 논문이었습니다. 저도 요새 depth 추정을 할 때 물리적인 cue를 어떻게 주면 좋을까 고민이 많았는데, 해당 논문이 저의 고민을 조금 해결해주지 않았나 싶네요. 다만 성능 개선은 생각보다 미미해서 조금 아쉽긴 합니다. 해당 논문의 아이디어를 잘 보완해서 성능 개선을 더 크게 할 수 있지 않을까 싶네요.
안녕하세요 신정민 연구원님 좋은 리뷰 감사합니다.
monocular depth estimation이라는 task부터 논문의 방법론까지 한 번에 이해할 수 있는 글인 것 같습니다.
특히 방향 정보와 depth간의 관계를 추측하고, 이를 첫 번째 표의 실험을 통해 수직 방향이 depth정보와 더 관련있다는 것을 명시적으로 확인한 뒤 이를 직접적으로 고려한 방법론을 제안한 것이 인상적이었습니다.
Direction-aware feature extraction 부분에서 궁금한 점이 있는데요, 설명해주신 바에 따르면 feature map에 affine연산을 적용한 뒤 conv 연산을 진행하고, affine 연산을 반대로 수행하는 것인 듯 한데요, 그렇다면 결국 그냥 conv연산을 수행한 것과 동일한 것이 아닌가요?
단순히 생각해 보았을 때 처음 feature map에 적절한 가중치를 곱하여 Direction-aware와 동일한 output을 낼 수 있을 것 같아 중간의 affine 연산이 어떤 의미가 있는지 잘 모르겠습니다…
안녕하세요.
컨볼루션 연산이 보통 3×3 필터 사이즈를 통해 주변 이웃 픽셀들의 가중합을 수행하게 되는데, 이때 affine matrix를 적용한 특징 맵의 경우 적용이 안된 특징 맵과는 다른 형태(가령 scene 전반적인 변형)로 구성이 되어 있어서 주변 이웃픽셀들의 구조 역시 상이해지므로 다른 컨볼루션 연산 결과를 지니게 됩니다.
따라서 affine matrix를 적용한 후 컨볼루션은 적용한 다음 inverse matrix를 곱한다고 해서 convolution만 적용한거랑 결과값이 같아질 수 없습니다.
감사합니다.