안녕하세요, 이번에는 김태주 연구원님께서 6D Pose estimation task와 한 번 접목시켜보도록 공부해보라고 하셨던 조언을 듣고, 다들 알고 계실 것 같은 NeRF를 리뷰해봤습니다. 카메라 기반의 방법론이다보니 수식이 되게 많은 것 같습니다.

0. Preliminary

먼저 NeRF의 전체적인 흐름은 다음과 같습니다.

1. N개의 이미지가 input으로 들어감
2. SfM(Structure From Motion) 과정을 거침
3. NeRF 모델을 사용하여 view synthesis를 만듦

해당 과정이 전체적인 파이프라인이 되고, 해당 논문에서 전반적으로 다루는 내용들은 3번 과정의 내용들입니다. NeRF를 수행하기 위해서는 어디에서, 어떤 방향에서 촬영되었는지 알아야 진행할 수 있게 되는데요. 2번 과정을 통해 촬영한 이미지의 카메라 파라미터를 추출해주어야 합니다.

SfM 과정을 간략하게 설명해보면 앞서 얘기했듯이 카메라의 파라미터 값을 추출하기 위해 진행하는 과정입니다. 먼저 2-view의 이미지를 가지고 이미지의 특징점을 추출하고 이때, 비슷한 특징을 갖는 것끼리 Feature Matching을 수행합니다. Feature Matching으로 얻은 feature간의 correspondence를 찾기하기 위해서는 Epipolar Geometry가 필요하게 되는데요. 이때, outlier를 제거하기 위한 RANSAC 과정을 반복하면서 가장 많은 inlier을 가질 때 Fundamental matrix를 최종적으로 사용하게 됩니다. Essential matrix는 구하기 위해 해당 Fundamental Matrix와 Intrinsic Matrix를 곱하면 구할 수 있게 됩니다.

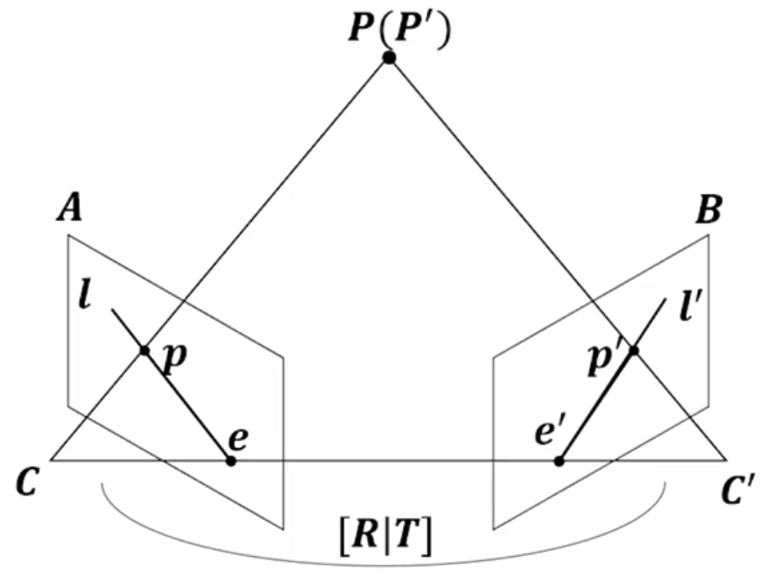
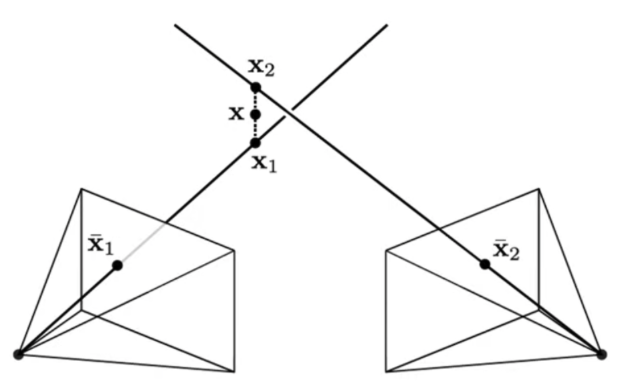
그 다음으로 Triangulation 과정입니다. 두 이미지 간의 Feature에 대한 Correspondence를 추정했으니 이제 3D point를 생성해줍니다.

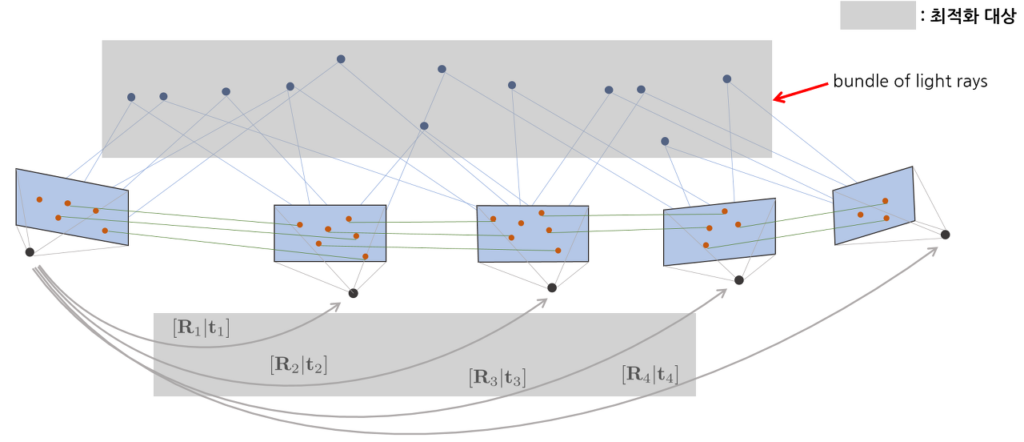
마지막으로 Bundle adjustment 과정을 거쳐 여러 장의 이미지셋을 합쳐 사용하게 됩니다. 해당 과정을 통해 3D point를 생성하고 2D로 reprojection 시켜 기존 2D 특징점과 비교했을 때에 대한 reprojection error를 계산하여 error을 최적화 하는 과정을 수행합니다.

이제 SfM을 통해 카메라의 파라미터를 알아내었으니, NeRF가 동작하기 위한 준비가 다 되었습니다.

NeRF 리뷰 시작하겠습니다.

1. Introduction

이번 논문에서는 다양한 viewpoint에 대한 이미지의 rendering error를 최소화하기 위한 연속적인 5D scene representation의 파라미터를 직접적으로 최적화하여 새로운 방식으로 view synthesis의 오랜 문제를 해결합니다. 여기서 말하는 view synthesis란 N대의 카메라를 통한 input이 들어가면 continuous하게 임의의 시점에서 본 대상의 모습을 합성하는 아래와 같은 task를 의미합니다.

이러한 view synthesis에서 가장 중요하게 다루어야 하는 부분은 카메라의 위치가 바뀐다고 해서 이미지를 단순히 crop 하거나 shift 해서 표현하는 것으로 끝나는 것이 아니라 depth에 따라 멀리 있는 대상은 카메라의 이동에도 크게 많이 안 움직이지만 가까이에 있는 물체는 많이 움직이는 것처럼 움직이는 정도가 다른 것을 영상을 통해 확인하실 수 있습니다. 이러한 현상을 Parallax Effect라고 한다고 합니다. 즉, 카메라 입장에서 픽셀 이동이 가까우면 많이 생길 것이고, 멀 경우 적게 생길 것이라는 현상을 가지는 것이라고 이해하시면 되겠습니다. 이러한 현상들을 고려하기 위해서는 3D space에 대한 이해가 필요할 것 같습니다.

전체적인 NeRF에서 제안하는 시나리오를 살펴보면 다음과 같습니다.

N개의 시점에서 찍은 2D 이미지를 입력으로 주게 되고, 이를 continuous 하게 임의의 시점에서 찍은 2D 이미지를 만들어 내고 최종적으로 rendering 해주는 과정을 거치게 되면 저희가 원하는 NeRF representation을 얻을 수 있게 됩니다.

해당 논문에서의 contribution을 정리해보면 다음과 같습니다.

• complex geometry와 물체가 있는 연속적인 장면을 기본적인 MLP로 파라미터화된 5D Neural Radiance Field로 representation 하기 위한 접근 방식을 제안함
• 당시에 사용되었던 고전적인 volume redering 기법과는 다른 redering 절차를 적용하여, RGB 이미지에서 NeRF representation을 최적화하는 데 사용함 (hierarchical sampling strategy 포함)
• 각 입력 5D coordinate를 고차원 공간에 매핑하는 positional encoding을 통해 NeRF를 성공적으로 최적화하여 높은 퀄리티의 representation을 할 수 있었음

2. Related Work

Neural 3D shape representations

당시 진행되었던 연구들에서는 signed distance function 또는 occupancy field에 xyz 좌표를 매핑하는 딥러닝 네트워크를 최적화하여 level set으로 연속적인 3D shape를 implicit representation하는 방법이 연구되었습니다. 그러나 이러한 모델은 일반적으로 ShapeNet과 같은 합성 3D shape 데이터셋에서 얻은 GT 3D geometry를 고려해야 한다는 제약이 있었다고 합니다. 후속 연구에서는 2D 이미지만을 사용하여 Neural implicit shape representation을 최적화할 수 있는 이전 연구와 다른 rendering 함수 공식화하여 GT 3D shape에 대한 문제를 해결했었습니다. 또 다른 연구에서는 surface를 3D occupancy field로 representation하고 수치적으로 접근하여 각 ray에 대한 surface 교차점을 찾은 다음에, implicit differentiation을 계산합니다. 각 ray의 교차점은 해당 지점의 색상을 예측하는 3D texture field에 입력으로 제공하였습니다. 각 연속적인 3D 좌표에서 단순히 특징 벡터와 RGB 색상을 출력하는 하는 연구도 진행되었습니다.

이러한 기법들은 잠재적으로 복잡한 high-resolution geometry를 표현할 수 있지만, 지금까지는 geometric complexity가 낮은 단순한 shape으로 제한되어 지나치게 부드러운 rendering을 결과로 내었다고 합니다. 저자는 네트워크를 최적화하여 5D radiance field(2D-view에 따라 모양이 달라지는 3D volume)를 인코딩하는 다른 방법을 사용하면 더 높은 해상도의 geometry와 shape을 표현하여 복잡한 scene의 새로운 view를 사실적으로 rendering할 수 있음을 보여 주었다고 합니다.

View synthesis and image-based rendering

volumetric representation을 사용하여 입력 RGB로부터 고품질의 view synthesis task를 처리합니다. volumetric을 사용하여 복잡한 shape과 material을 사실적으로 표현할 수 있고, gradient-based 최적화에 적합하며, mesh-based 방식에 비해 시각적으로 방해되는 artifact를 덜 생성하는 경향이 있습니다. 이러한 volumetric 기법은 새로운 view synthesis에서 인상적인 결과를 얻었지만, discrete sampling으로 인한 시간과 공간의 복잡성으로 인해 고해상도 이미지로 확장하는 부분에 대해서는 제약이 있었다고 합니다.

3. Neural Radiance Field Scene Representation

해당 논문에서 등장하는 5D representation의 구성은 3D location인 \mathbf x=(x,y,z)와 2D viewing direction을 의미하는 (\theta, \phi)로 되어있습니다. 이러한 정보를 input으로부터 MLP를 통과한 output으로는 color(RGB)를 의미하는 \mathbf c=(r, g, b)와 density \sigma가 되게됩니다. Direction을 의미하는 unit vector를 \mathbf d라고 할 때, MLP 네트워크를 통과하여 continuous한 5D scene representation을 F_{\Theta}:(\mathbf x, \mathbf d) \rightarrow (\mathbf c, \sigma)로 근사할 수 있고, weight를 의미하는 \Theta는 각 5D coordinate에 대해 대응하는 volume density와 directional color에 대한 가중치를 고려하여 최적화를 할 수 있게 됩니다. 즉 NeRF라는 것은 결국 각 위치 (x, y, z)와 direction d가 입력으로 들어왔을 때, RGB와 density를 계산할 수 있도록 하는 모델링 함수를 제안했다고 이해하시면 될 것 같습니다. 앞서 언급한 notation을 좀 더 살펴보면, d는 3D 공간에서 물체를 다양한 시점에서 본다고 생각을 해보면, 물체를 보는 방향에 따라 물체의 색상이 변하게 될 것 입니다. 예를 들면, 저희가 거울을 여러 시점으로 본다고 했을 때, 거울에서 가지는 정보는 시점에 따라 달라지게 됩니다. 이처럼, 물체의 색상 정보가 변하게 되므로 방향 정보도 input에 포함을 시켰습니다.

Density를 설명하기에 앞서 해당 논문에서 중요하게 다루는 Ray에 대한 설명을 먼저 하겠습니다.

다양한 viewpoint 중, 하나의 viewpoint를 보았을 때를 위 그림과 같이 나타내었을 때, 3D point에 대응하는 2D pixel 영역에 projection을 하게 되는데, 이를 논문에서는 Ray라고 정의합니다. 그림에서는 주황색 선을 의미하겠네요.

Ray 위에 있는 하얀점들은 수많은 sample들이고 Ray는 sample들의 집합이라고 해석도 가능할 것 같습니다. 해당 논문에서는 하얀점들을 particle이라고 명시하였습니다. 해당 particle들의 의미는 RGB를 구성하는 요소인데요. 해당 부분에서 density라는 내용이 나오게 됩니다. 이전의 방향 정보를 통해 저희는 해당 지점에 대한 density를 알 수 있는데요. density는 분포 정도를 나타내지만 해당 내용에서는 투명도라고 생각하시면 이해하시는 것에 도움이 될 것 같습니다.

NOTE ; 그렇다고 정말로 투명도를 의미하는 것은 아니고, 이해를 돕기 위한 단어라고 생각하시면 되겠습니다. 저희가 생각하는 분포의 개념이 맞습니다.

즉, 앞에 있는 particle의 density가 큰 경우, 투명도가 적으므로 뒤에 있는 particle 들은 색상이 잘 안 보이게 되고, 앞에 있는 particle의 density가 작은 경우, 투명도가 크므로 뒤에 있는 particle 들은 색상이 잘 보일 것입니다.

이러한 방향 정보를 넣었기 때문에 그림(4)의 GT는 빛 반사가 되는 것을 확인할 수 있는 반면,  No View Dependence는 빛 반사가 안되는 것을 확인할 수 있습니다.

4. Volume Rendering with Radiance Fields

이번에는 Volume Rendering을 어떻게 진행을 했는지 살펴보겠습니다.

volume rendering도 사실 대단한 건 아니고 앞서 다루었던 내용과 더불어 색상 정보의 가중치를 어떻게 줄 것인지에 대한 과정이라고 생각하시면 되겠습니다. 앞서 설명드린 Ray가 있었습니다. Ray를 수식으로 정의하면 \mathbf r(t)= \mathbf o + t \mathbf d라고 합니다. Ray의 원점은 초점이므로, 초점으로부터 \mathbf d 방향으로 t만큼 이동한 정도를 의미합니다. 해당 Ray는 결국 particle들이 있는 집합이었는데요. 3D point와 2D pixel을 잇는 직선이었던 것도 확인을 하였습니다. 즉, Rendering은 물체가 주어지면 특정 viewpoint에서 카메라 위치와 pixel 위치가 정해졌을 때, 두 지점을 잇는 직선(Ray)가 정의되고 해당 직선 위의 있는 모든 Particle들이 해당 점의 RGB를 구성하도록 하는 것입니다. 이때, Ray 위에 존재하는 particle들의 weighted sum을 해야 해당 pixel의 색상을 정할 수 있습니다. 그럼 weight는 어떻게 정의할까요?

다음과 같이 정의를 할 수 있습니다.

1. Density가 클수록 Weight는 커져야 함 → \sigma(\mathbf r(t))
2. 해당 지점을 가로막고 있는 점들의 Density 합이 적을수록 weight가 커져야 함 → T(t)

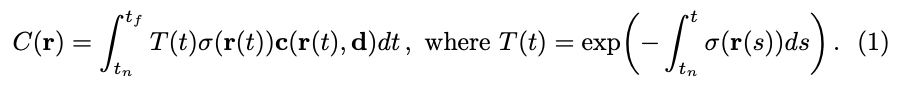
식(1)을 살펴보면 C(\mathbf r)은 저희가 최종적으로 얻는 RGB정보입니다. Ray에서 물체와 가장 가까운 것을 near t_{n},물체와 가장 먼 것을 far t_f로 표현하였습니다. 식 안의 \mathbf c(r(t), d)와 \sigma(\mathbf r(t))는 input으로 들어오는 정보로 MLP를 통과하여 얻을 수 있습니다. weight 정의 중 첫 번째 의미는 뒤에 있는 particle들은 잘 보이지 않게 되므로 해당 particle에는 weight를 크게 주도록 하겠다는 의미입니다. 두 번째는 사람을 찍고 있는 카메라 사이에 벽이 있다고 가정을 해봅시다. 이때, 특정 viewpoint에서는 ray를 projection 했을 때 벽 때문에 뒤에 있는 사람이 보이지 않을 것입니다. 그럼 벽까지의 density가 높을 것인데, 저희는 사람을 타겟으로 하기 때문에 벽쪽에 있는 density가 작아져야 사람이 보이게 된다는 것입니다. 즉, 벽까지의 density의 합이 크면 불투명하므로 weight는 줄이고, density의 합이 작으면 투명하므로 해당 weight는 증가시킵니다. 해당 T(t) 같은 경우, accumulated transmittance라고 합니다. 해당 식을 살펴보면 음수형태의 exponential이므로 density가 클수록 weight가 감소하고 density가 클수록 weight가 증가하도록 설계한 것을 확인할 수 있습니다.

하지만, 이러한 과정에도 문제가 있는데요. implementation 과정에서 문제가 발생하게 됩니다. 식(1)과 같은 경우, continuous한 integral이므로 모델링을 위한 implementation을 하려면 discrete한 식으로 변환을 해주어야 합니다.

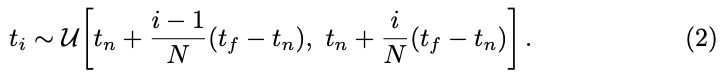
식(2)를 살펴보면 앞서 언급한 ray에서 [t_{n}, t_{f}]를 균등한 간격의 N개의 bin으로 분할한 다음에 각 bin 내에서 1개의 sample을 uniform distribution으로 추출하는 방식을 사용하였다고 합니다.

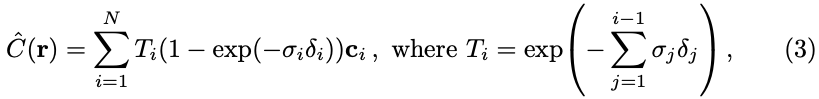
random sampling을 거친다음에 식(3)와 같이 식을 변환하게 됩니다. integral을 \Sigma형태로 바꾸었고, 앞서 구한 Ray 따라서 적분하는 것을 discrete하게 하도록 하는 term을 [1]논문을 참고하여 적용하였다고 합니다. 즉, i부터 까지 증가하면서 Continuous한 식과 근사한 값이 된다고 합니다. 해당 식이 저희가 원하는 최종적으로 예측한 컬러 정보가 됩니다.

[1] Max, N.: Optical models for direct volume rendering. IEEE Transactions on Visualization and Computer Graphics (1995)

5. Optimizing a Neural Radiance Field

기존의 MLP만으로는 성능이 좋지 않았다고 합니다. 이러한 문제를 해결하기 위해 저자는 두 가지의 방법론을 적용하게 됩니다.

5.1. Positional encoding

해당 section에서의 결론은 low-dim을 input으로 사용했더니 성능이 안 좋아서 high-dim으로 넣었더니 성능의 향상이 있었다 라는 것이 핵심입니다. 어떻게 dimension을 확장하였는지 알아보도록 하겠습니다.

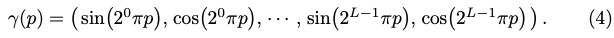
식(4)와 같이 sine과 cosine으로 이루어진 식을 x, y, z를 입력으로 여러 개를 만들어 차원을 증가시켰다고 합니다. 이렇게 차원을 늘리면 선명도에 대한 문제가 어느정도 완화시킬 수 있었다고 하네요. 해당 식에는 L이라는 파라미터가 사용되게 되는데요. 위치 (x, y, z)에 대해서는 L=10을 사용하여 60-dim을 만들었고, 방향 \mathbf d에 대해서는 24-dim을 사용했다고 합니다.

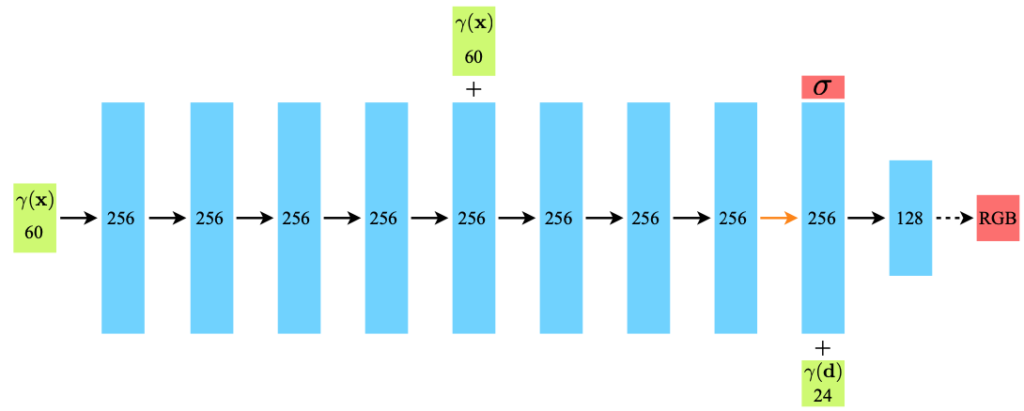
위 그림과 같이 FC layer로 이루어진 network를 사용했다고 하네요.

5.2. Hierarchical volume sampling

Ray 상의 particle 또한 성능에 영향이 있으므로 저자는 해당 과정에서 2개의 네트워크를 사용하게 됩니다. Coarse Network C_{c}와 Fine Network C_{f}를 사용합니다. 첫 번째로 N_{c}개의 t를 뽑고 Coarse Network를 학습을 시킵니다. 이때 우리는 앞서 식(3)을 보면 T_{i}(1-\exp(-\sigma_{i}\delta_{i}))의 weight를 얻을 수 있게 됩니다. 해당 weight은 c_{i}의 분포라고도 해석을 할 수 있다고 합니다. 이러한 Coarse Network를 통해 아래와 같은 distribution을 얻었다고 할 때, peak지점이 있는 영역이 이미지 내의 타겟이 존재하는 영역이라고 말을 할 수 있습니다. 해당 영역을 추가적으로 더 뽑기 위해 N_f개를 뽑아서 총 N_{c} + N_{f}개의 sample을 이용하여 fine network를 학습시켜서 사용하게 됩니다.

5.3. Implementation details

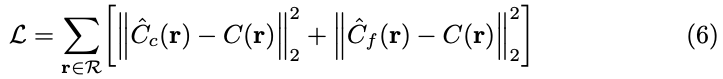
학습은 식(6)과 같이 이루어지게 됩니다. 이전에 구한 coarse 단계에서 volume sampling 추정한 값과 GT를 빼고 fine 단계에서 volume sampling을 추정한 값과 GT를 뺀 값에 대한 각각의 l_{2} loss를 구하고 더한 값을 loss function으로 사용합니다.

6. Results

그림(4)는 모든 모델을 사용했을 때와 positional encoding을 사용했을 때의 성능 변화를 볼 수 있습니다.

6.1. Comparisons

결과들을 보면 당시 view synthesis를 다루던 논문들과 비교해봤을 때 많이 개선된 것을 확인할 수 있습니다.

6.2. Ablation study

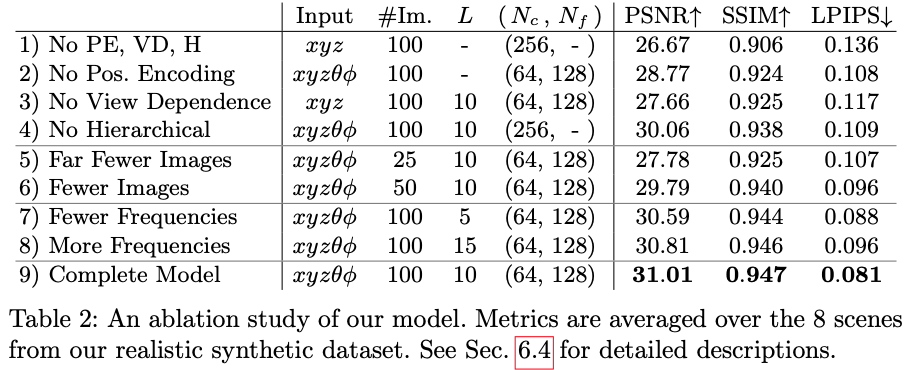
마지막으로 저자가 제안한 방법을 적용하는 것과 이미지의 개수, frequency에 대한 ablation study를 진행한 표입니다. 저자가 제안한 방법론들을 모두 적용한 맨 마지막 행의 성능이 가장 좋은 것을 확인할 수 있습니다.

7. Conclusion

이번 논문에서는 MLP를 사용하여 물체와 scene을 continuous한 function으로 표현하는 이전 논문들의 문제들을 직접적으로 해결합니다. 저자는 scene을 5D Neural Radiance Field(3D location 및 2D viewing direction의 함수로 volume density와 view에 따라 projection시키는 Ray를 출력하는 MLP Network)로 표현하는 것이 discrete된 voxel 표현을 출력하기 위한 CNN을 훈련하는 기존 방식보다 더 나은 rendering을 생성한다는 사실을 입증했습니다. 저자는 rendering의 sample 효율을 높이기 위해 Hierarchical volume sampling을 제안했지만, NeRF를 효율적으로 최적화하고 rendering하는 기술을 연구하는 데는 아직 더 많은 진전이 있어야 한다고 하면서 논문을 마칩니다.