안녕하세요, 이번 X-Review는 직전 세미나에서 소개해드렸던 22년도 CVPR 논문 <Probabilistic Representations for Video Contrastive Learning>을 주제로 준비하였습니다. 사실 세미나라는 것이 짧은 시간 내 방법론의 배경과 핵심적 내용을 모두 전달하기에 어려울 뿐만 아니라, 듣는 분들 입장에서도 낯선 컨셉에 대해 바로 납득하기 힘들다는 것을 저도 잘 알고 있기에 글로 남기고자 합니다. 물론 이번 Access 작업의 핵심 컨셉이 될 확률적 임베딩과 관련된 논문이기에 저 스스로도 정리하고자 하는 목적도 있습니다.

Self-supervised Video Representation Learning (SSVRL)
본 논문은 비디오 분야의 Self-supervised Video Representation Learning task를 수행합니다. 이는 비디오의 어떤 라벨도 가지지 않은 채로, backbone 모델이 비디오의 일반적 표현력을 가질 수 있도록 학습시키는 것입니다. 각 방법론대로 사전학습을 마치면 그 방법론이 유효했는지, 즉 모델이 추출하는 feature가 일반적인 표현력을 가지게 되었는지 알아보기 위해 Action recognition(video classification), Video retrieval 등의 근본적인 downstream task로 평가하게 됩니다.
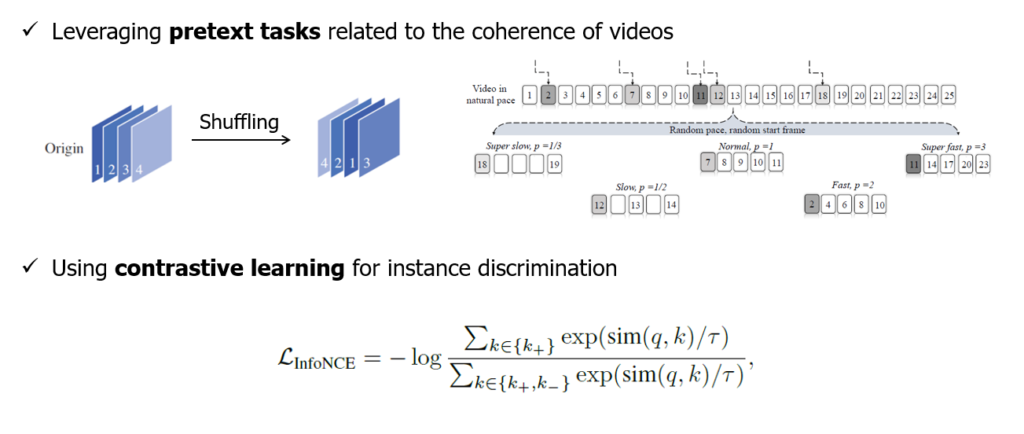
본 task는 크게 두 갈래로 나뉘어집니다. 첫 번째는 pretext task 기반의 방법론들입니다. 이는 위 그림의 상단에서 볼 수 있다시피 데이터셋 단위의 라벨이 없는 상황에서 임의로 프레임 순서를 섞고, 그것을 ‘천연 라벨’ 삼아 부수적인 분류 task(pretext task)를 진행하는 과정에서 모델이 비디오에 대한 정보를 학습하도록 설계하는 방식에 해당합니다. 순서를 섞는 것 이외에도 sampling rate를 다르게 주어 비디오의 재생 속도를 변화시키고 이 변화를 맞추는 방식 등 다양하게 제안되어왔습니다.
다음은 contrastive learning 기반의 방법론들입니다. 그림의 아래 부분과 같이 InfoNCE loss 등의 contrastive loss를 기반으로 모델의 표현력을 학습합니다. 여기서는 사실 라벨이 전혀 없는 상황 속에서 positive와 negative set을 어떻게 지정해줄 것인지가 중요할 것입니다. 오늘 소개해드릴 방법론은 contrastive learning을 기반으로 합니다.
일반적으로 pretext task 기반 방법론들은 연구 초창기인 19~21년도에 활발히 연구되었고, 그 이후부터는 contrastive learning 기반의 방법론들이 현재까지 주를 이루고 있습니다. 물론 최근 논문 중에도 pretext task 방식을 다시 분석하여 좋은 성능을 내는 방법론도 있는 것으로 알고 있습니다.
아래 목록은 기존에 제가 작성했던 SSVRL task 관련 X-Review이고, 임근택 연구원님과 이광진 연구원님께서 더욱 최신의 방법론까지 다루시니 그 또한 참고하시면 도움이 될 것으로 생각합니다.
- [CVPR 2022] Learning From Untrimmed Videos: Self-Supervised Video Representation Learning With Hierarchical Consistency
- [AAAI 2022] Self-Supervised Spatiotemporal Representation Learning by Exploiting Video Continuity
- [CVPR 2021] Self-supervised Motion Learning from Static Images
- [CVPR 2022] Frame-wise Action Representations for Long Videos via Sequence Contrastive Learning
- [NeurIPS 2020] Self-supervised Co-training for Video Representation Learning
- [CVPR 2021] Self-supervised Video Representation Learning by Context and Motion Decoupling
- [WACV 2021] Unsupervised Video Representation Learning by Bidirectional Feature Prediction
SSVRL task도 워낙 방법론끼리 세부 컨셉이 달라 큰 개념에 대해서만 간단히 소개해드렸고, 이제 논문으로 들어가보겠습니다.
1. Introduction
Video representation learning은 비디오 내 존재하는 시공간적 콘텐츠를 파악한다는 관점에서 다양한 downstream task 및 실용적 측면에서 중요합니다. 이 때 영상의 개별 annotation에 대한 cost도 만만치 않아 줄이기 위한 연구들이 다양하게 수행되고 있다는 점을 다들 아실텐데요, 시간 축까지 포함하고 있는 비디오에 대한 개별 annotation을 주는 것은 더욱 cost가 크고, 실제로 annotation 되어 있는 비디오보다 웹 상에서 얻어 활용할 수 있는 비디오가 훨씬 많기에 self-supervised 기반의 video representation learning은 컴퓨터비전 분야에서 반드시 필요하다고 볼 수 있습니다.
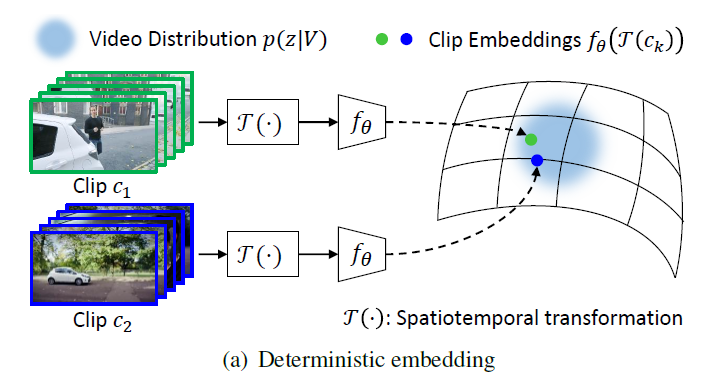
위에서 제가 설명드린 SSVRL의 두 가지 갈래인 pretext task 기반과 contrastive learning 기반 방법론들은 모두 deterministic representation을 활용한다고 볼 수 있습니다. Deterministic representation 또는 embedding이라는 것은 위 그림 1 – (a)와 같이 저희가 3D backbone 모델을 통해 clip에 대한 하나의 feature를 추출하는 모든 상황을 의미하는데, 이러한 상황 저자는 기존 contrastive learning 기반 SSVRL 프레임워크 자체와 더불어 아래 3가지의 문제점을 갖는다고 지적합니다.
Limitations of deterministic representations for video contrastive learning
- “비디오”라는 데이터 자체가 noisy한 temporal dynamic을 갖고 temporal redundancy(연속되는 프레임 간 중복성)가 크기에, 이를 결정적으로 embedding하는 것은 다양성을 모델링하지 못한다.
- 일반적으로 contrastive learning의 positive pair를 구축하기 위해 비디오에서 샘플링한 clip(16프레임 묶음 단위)에 spatiotemporal augmentation을 적용하는데, 기존 프레임워크에서 사용하던 temporal augmentation 중 하나인 shuffling은 오히려 비디오의 고유한 특성을 망쳐 방해가 된다.
- 기존 방식에서 positive, negative pair를 구축하기 위해 anchor clip을 기준으로 같은 비디오에서 얻은 clip은 positive, 다른 비디오에서 얻은 clip은 negative로 지정하는데, 이렇게 되면 실제로는 의미론적으로 유사한 clip에 대해서도 다른 비디오에서 추출했다는 이유만으로 representation의 유사도가 작아지는 방향으로 학습하게 된다.
위와 같은 기존 결정적 embedding 방식의 단점을 극복하고자, 저자는 Probabilistic representations for Video Contrastive learning, ProViCo 프레임워크를 제안하게 됩니다.
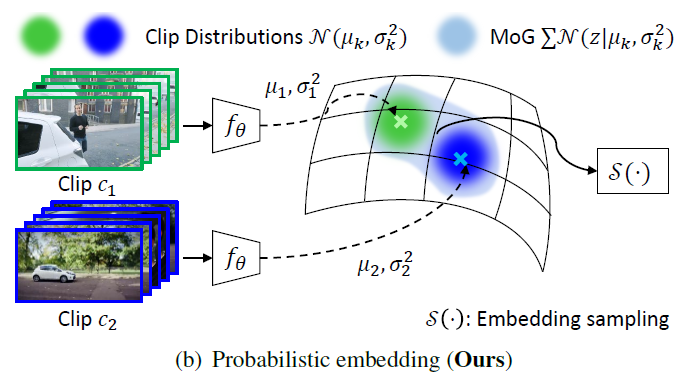
결정적 embedding을 활용하는 그림 1 – (a)에 비교하며 확률적 embedding을 활용하는 그림 1 – (b)를 보면, 우선 인코더 f_{\theta{}}를 통해 clip에 대한 가우시안 분포의 평균 \mu{}와 분산 \sigma{}^{2}을 얻어 확률적 embedding space 상에서 결정적이지 않은 특정 분포로 표현하는 것을 볼 수 있습니다. 또한 spatiotemporal transformation 과정이 사라졌습니다. Clip을 분포로 표현함으로써 비디오 내 충분히 다양한 상황에 강인하게 동작할 것을 기대하며, 비디오에 내재된 특성을 망칠 수 있는 기존의 augmentation을 제거한 것입니다.
그리고 기존의 방식인 그림 1 – (a)에서는 clip 간 contrastive learning을 수행했다면 본 방법론에서는 가우시안 분포로 표현한 clip을 Mixture of Gaussian(또는 Gaussian Mixture Model)으로 엮어 하나의 비디오로 표현하고, 비디오 단위의 contrastive learning을 수행할 수 있게 됩니다. 더불어 확률적 embedding 공간 상에서의 거리를 측정하고 positive, negative set을 지정해주며 다른 비디오로부터 얻은 clip이 무조건 negative로 들어가는 문제 상황을 어느 정도 해결할 수 있게 됩니다. 이렇게 positive, negative set을 지정한 뒤 contrastive learning을 수행할 때 분포의 분산을 uncertainty로 지정하고 활용함으로써 각 instance의 reliability에 따른 instance discrimination 정도를 조절해주는 stochastic contrastive loss까지 적용하였습니다.
ProViCo의 contribution을 정리하면 아래와 같습니다.
- Effectively represent the probabilistic video embedding space
- Probabilistic distance-based positive mining to exploit semantic relations between videos
- Present the stochastic contrastive loss to weaken the adverse impact of unreliable instances through the uncertainty estimation
아직은 전반적인 프레임워크가 추상적이니 수식과 함께 방법론 부분을 살펴보겠습니다.
2. Method
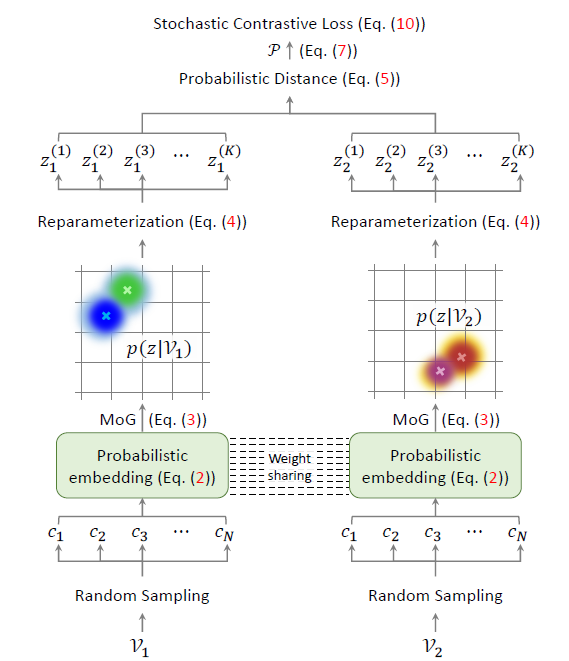
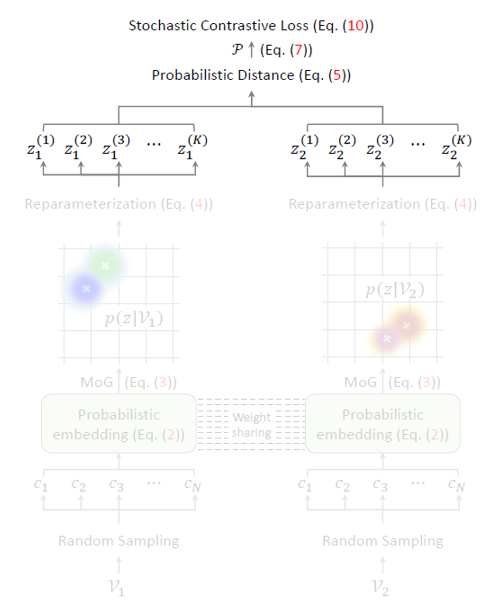
그림 2는 ProViCo의 전체 프레임워크를 보여줍니다.
- 2.1 Probabilistic Video Embedding
맨 처음 비디오로부터 랜덤 샘플링한 clip의 확률적 embedding을 얻고, 이를 MoG(Mixture of Gaussian)으로 엮어 비디오에 대한 확률적 embedding을 만들어줍니다. 이후엔 contrastive learning을 수행 대상을 얻어야 하니 비디오 분포(MoG)에서 reparameterization trick을 통해 샘플링을 수행합니다. - 2.2 Mining Positive and Negative Pairs
이렇게 샘플을 얻었으면 contrastive learning을 수행하기 위해 확률적 embedding 공간 상에서의 거리에 따라 positive, negative set을 구축해야 합니다. - 2.3 Stochastic Contrastive Loss
이제 샘플과 positive, negative pair를 구축했으니 contrastive learning을 수행하면 되겠죠. 앞서 말씀드린대로 분포의 분산을 uncertainty로 두고 instance discrmination의 정도를 조절하게 됩니다.
한 절씩 쪼개어 자세히 알아보겠습니다.
2.1 Probabilistic Video Embedding
ProViCo에서 clip을 확률적으로 embedding한다는 것은 clip이 정규분포 형태를 가질 것으로 가정한 뒤 이에 대한 평균 \mu{}와 분산 \sigma{}^{2}을 얻는다는 의미입니다.
Notation을 먼저 정리하고 시작하겠습니다.
하나의 비디오 \mathcal{V}로부터 총 N개의 clip \{c_{1}, \cdots{}, c_{N}\}을 랜덤으로 샘플링해줍니다. 이 때 v_{c_{n}} = f_{\theta{}}(c_{n})은 clip c_{n}을 backbone f_{\theta{}}에 태워 얻은 결정적 feature를 의미합니다. 결정적 feature v_{c_{n}}에 대한 가우시안 분포 p(z|c_{n})의 \mu{}와 \sigma{}^{2}를 얻기 위한 과정은 아래 수식 (2)와 같습니다. 여기서 z는 확률적 임베딩 공간이라고 생각하시면 됩니다.
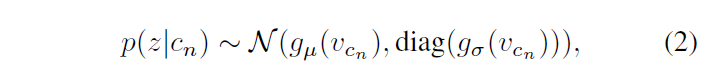
일반적으로 \mathcal{N}(x, y)는 평균 x, 표준편차 y를 갖는 정규분포를 의미한다는 것은 알고 계실것입니다. 그렇다면 수식 (2)에서 g_{\mu{}}(v_{c_{n}})이 clip 분포의 평균, \text{diag}(g_{\sigma{}}(v_{c_{n}}))이 clip 분포의 표준편차를 의미하는 것입니다. g_{\mu{}}, g_{\sigma{}}는 아래와 같이 정의됩니다.
- g_{\mu{}} = FC1 + LayerNormalization + L2 Normalization
- g_{\sigma{}} = FC2
두 encoder의 구조가 다른 이유는, 확률적 임베딩을 적용하는 이전 논문을 살펴보니 표준편차의 경우 clip 또는 video instance의 uncertainty로 쓰이는데 이 때 normalization을 적용해주는 경우 분포가 깨지며 uncertainty로 활용하기 어려워지기 때문이라고 합니다.
이제 비디오에서 샘플링한 모든 clip을 수식 (2)에 따라 확률적으로 embedding 했다면 정규분포들을 MoG로 엮어 하나의 비디오를 확률적으로 표현(=p(z|\mathcal{V}))해주어야 합니다. 이는 아래 수식 (3)과 같습니다.
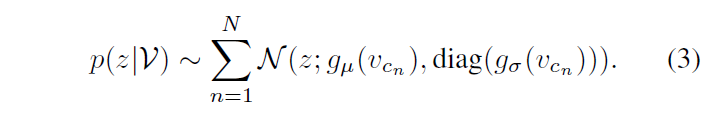
수식 (3)은 결국 총 N개의 정규분포를 모두 더하는 것이고, 이렇게 얻은 MoG의 확률밀도함수를 f_{\mathcal{V}}(z)라고 했을 때, \mu{}(\mathcal{V}), \sigma{}^{2}(\mathcal{V})는 아래 Appendix의 수식들과 같습니다.
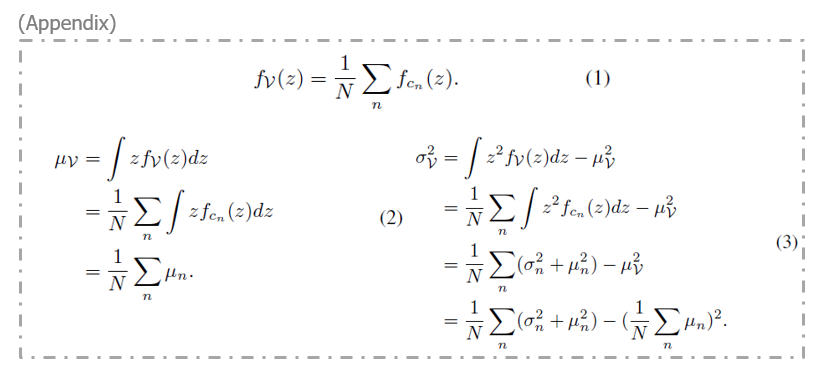
여기까지 수행했다면 아래 그림과 같이 하나의 비디오를 확률적으로 embedding 한 \mu{}(\mathcal{V}), \sigma{}^{2}(\mathcal{V})를 얻어낸 것입니다.
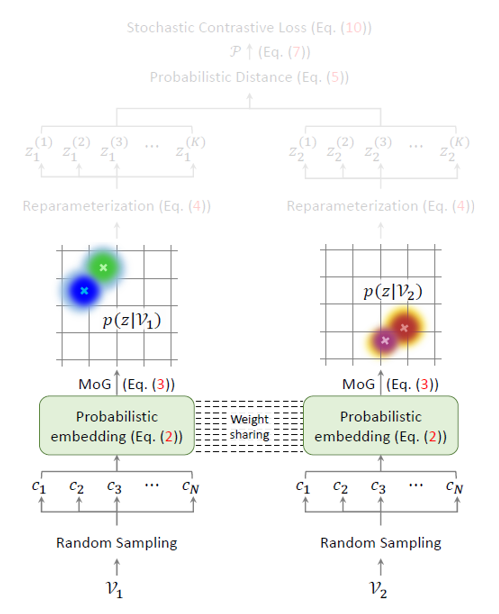
사실 이렇게 얻은 p(z|\mathcal{V})는 어디까지나 하나의 분포이기 때문에 실제 contrastive learning을 수행할 확률적 embedding 공간 상 K개의 실질적 feature \{z^{(1)}, \cdots{}, z^{(K)}\}가 필요하게 됩니다. 이는 아래 수식 (4)의 reparameterization trick을 통해 수행되고, 그림과 함께 설명드리겠습니다.
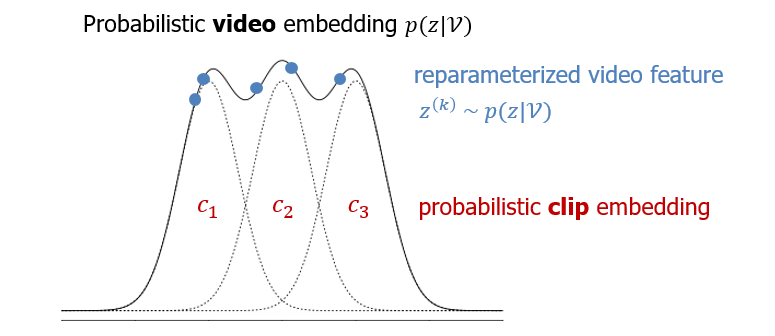
우선 논문에서 샘플링하는 clip의 개수 N=2이며 그림 2에도 2개의 정규분포가 모여 비디오 분포를 구성하는 것으로 나타나 있지만 이해를 돕기 위한 위 그림에서는 N=3으로 두었습니다. 3개의 clip 각각을 정규분포로 만들고 이는 점선으로 표현되어 있습니다. 이 점선들을 더해 만든 비디오의 분포 p(z|\mathcal{V})는 검정 실선으로 나타나있고, 지금 해야 하는 일은 저 분포로부터 실제 feature로서 사용할 샘플인 파란 점들을 K개 얻어야 한다는 것입니다. 그림 상에서 K=5인 것이고, 실제 방법론에서 사용하는 K=10입니다.
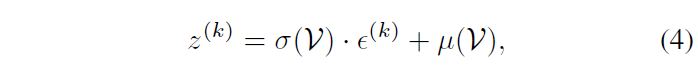
수식 (4)가 이 과정을 나타내는데, 여기서 \{\epsilon{}^{(1)}, \cdots{}, \epsilon{}^{(K)}\}는 단위 정규분포로부터 독립항등분포를 따라 추출된 랜덤 노이즈에 해당합니다. 이를 바탕으로 수식 (4)를 보면 MoG의 평균을 기준으로 표준편차에 \epsilon{}^{(k)}만큼 변형을 주고 더하는 형태인데요, 저자에 따르면 위 과정이 MoG의 “self-augmented” version을 얻어오는 것으로 볼 수 있다고 합니다. \epsilon{}이 독립항등분포를 따르기에 수식 (4)에 따라 얻은 총 K개의 샘플들도 MoG에서 독립항등분포를 따라 얻어질 것입니다.
여기까지 수행하여 확률적 embedding 공간 상 contrastive learning을 적용할 실질적 feature를 얻었습니다. 현재까지의 진행 상황은 아래 그림과 같으니, 이제 확률적 공간 상에서 거리를 측정하고 positive, negative set을 지정해 contrastive learning을 수행하면 됩니다.
2.2 Mining Positive and Negative Pairs
그럼 확률적 embedding 공간 상에서의 positive, negative pair를 지정하는 과정 중엔 어떤 detail들이 있을까요?
우선 간단하게 positive, negative set은 아래 수식 (6), (7)에 따라 정의됩니다.
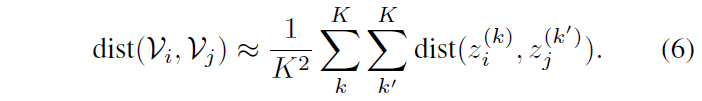
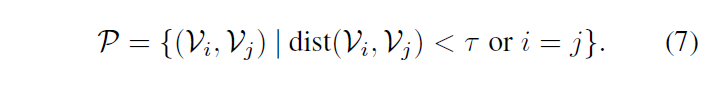
수식 (6)에서는 특정 거리 metric인 dist()에 따라 두 비디오 \mathcal{V}_{i}, \mathcal{V}_{j}에 대한 거리를 근사하는데, 이것이 실제 거리에 대한 ‘근사’인 이유는 앞 절에서 샘플링한 각 비디오의 MoG 별 feature z^{(k)}가 비디오의 분포 전체를 표현하지는 않는, 말 그대로 ‘샘플’이라서 Monte-Carlo estimation에 따라 가지고 있는 최대한 많은 수의 샘플을 바탕으로 측정한 거리이기 때문입니다.
여기서 거리 metric인 dist() cos 유사도가 될 수도 있고, 간단한 L2-distance가 될 수도 있습니다. 이 때 cos 유사도나 L2-distance는 분포의 평균만을 이용해 계산하게 되는데, 아래 그림 3의 toy example을 보면 L2-distance를 기준으로 평균 간의 거리를 측정하는 경우 붉은 분포 X_{2}를 기준으로 X_{3}가 X_{1}보다 더 가깝다고 판단되는 것을 볼 수 있습니다.
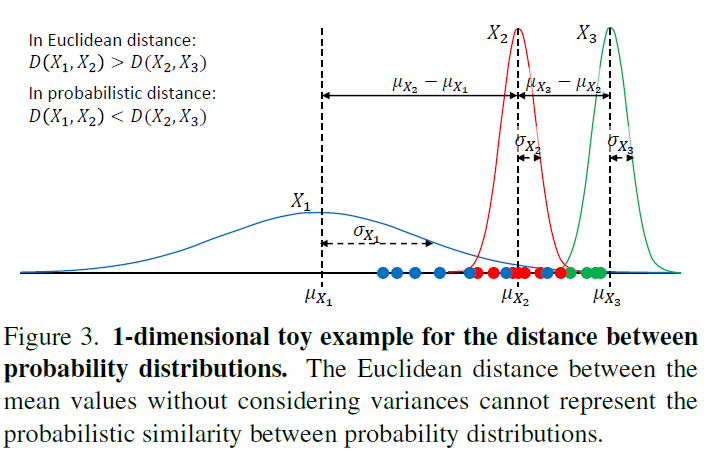
하지만 두 분포의 거리는 분산까지 고려해야 실질적인 분포 간 거리 내지는 유사도를 파악할 수 있고, 현재 과정이 positive sampling이라는 점을 감안했을 때 단순 L2-distance 또는 cos 유사도를 기준으로 삼는 것은 positive sampling에 적합하지 못하다고 볼 수 있습니다.
그래서 저자는 아래 수식 (5)에 해당하는 Bhattacharyaa distance를 거리 metric으로 차용하게 되고 이는 샘플 간 거리 뿐만 아니라 분포의 분산까지 고려하고 있는 것을 알 수 있습니다. 수식 (5)의 Bhattacharyaa distance를 사용하면 그림 3에서 X_{2}를 기준으로 X_{1}이 X_{3}보다 더 가깝다고 판단할 수 있게 되는 것입니다.
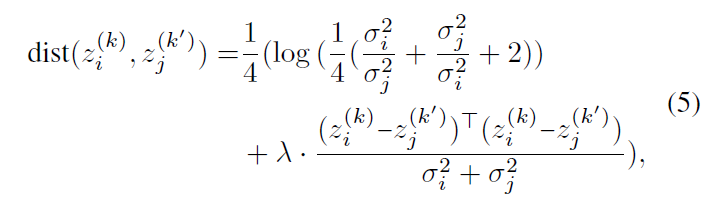
이후엔 수식 (7)에 따라 사전에 정의한 거리 threshold \tau{}를 기준으로 positive set \mathcal{P}를 구축하고, negative set은 positive set의 여집합 \bar{\mathcal{P}}가 됩니다. 물론 샘플 자기 자신도 \mathcal{P}에 포함되는 것을 볼 수 있습니다.
2.3 Stochastic Contrastive Loss
이제는 정말 contrastive learning을 통한 학습을 진행할 수 있게 되었습니다.
Soft contrastive loss
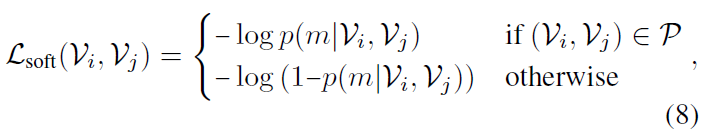
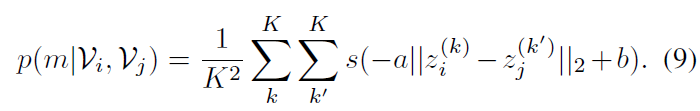
수식 (9)에서는 두 비디오 간의 매칭 확률 p(m|\mathcal{V}_{i}, \mathcal{V}_{j})을 구해주고, 이를 이용해 수식 (8)에서 contrastive learning을 수행하는 모습을 볼 수 있습니다. 이 때 수식 (8)의 \mathcal{L}_{\text{soft}}는 soft contrastive loss라고 불리게 되는데요, 그 이유는 아래 수식인 contrastive loss와 수식 (8), (9)의 차이점에 있습니다.
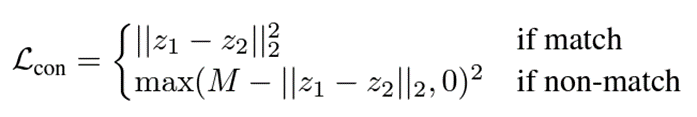
바로 위 수식인 기존의 contrastive loss는 negative에 해당하는 경우 두 샘플 간의 거리를 사전에 정의한 특정 threshold M만큼 멀어지게 해주는데, 이 M은 적절한 값을 찾아내기 매우 어려우며 어떤 값을 주느냐에 따라 성능 차이도 클 것입니다.
이 때 수식 (9)에 대해 부가적 설명을 드리자면, 식에서 s는 sigmoid, a와 b는 각각 양수, 실수에 해당하는 learnable vector입니다. a, b가 learnable vector라는 것은 a가 scaling, b가 shifting을 담당하여 거리를 얼마나 벌릴지에 대한 threshold를 학습 기반으로 얻는다는 의미입니다. 이것으로부터 기존 contrastive loss의 hard threshold M과 다르게 soft한 threshold를 가지기 때문에 soft contrastive loss라고 부르는 것입니다.
아무튼 다시 수식 (8)로 돌아가 \mathcal{L}_{\text{soft}}의 수렴 과정을 좀 살펴보겠습니다. 만약 두 비디오가 \mathcal{P} 관계인 경우 매칭 확률 p(m|\mathcal{V}_{i}, \mathcal{V}_{j})는 1로 수렴해야 합니다. 그것은 수식 (9)의 sigmoid 내부 값이 +\infty{}로 가야하고, 현재 a가 양수이기에 두 샘플 간 거리는 –\infty{}로 수렴하는 방향이 됩니다. 거리니까 0에 가까워지도록 수렴하게 되겠죠.
반대로 두 비디오가 \bar{\mathcal{P}}인 경우 수식 (9)의 sigmoid 내부 값이 –\infty{}로 가야하니 a가 양수인 점을 감안했을 때 두 샘플 간의 거리는 +\infty{}로 수렴하며 멀어지도록 만들어주는 것입니다.
Stochastic contrastive loss
이렇게 설명드린 방향으로 학습이 진행되는 것은 맞지만, 제가 Introduction에서 설명드린대로 비디오 각 샘플의 분산을 uncertainty로 두어 uncertainty 크기에 따른 \mathcal{L}_{\text{soft}}의 정도를 조정해주게 됩니다.
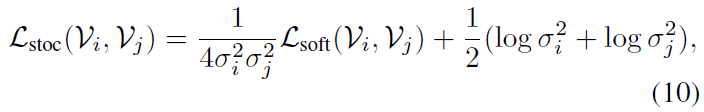
수식 (10)의 \mathcal{L}_{\text{stoc}}에는 앞서 본 \mathcal{L}_{\text{soft}} 앞뒤로 uncertainty term이 붙어있는 것을 볼 수 있는데요, 이를 해석해보면 만약 두 비디오 샘플의 uncertainty가 큰 경우 그리 신뢰할만한 instance들이 아니라고 판단하여 instance discrimination을 수행하는 \mathcal{L}_{\text{soft}}의 영향력은 줄이며 뒤 term에서 uncertainty를 줄여주는 방향으로 학습하게 됩니다. 반대로 두 비디오 샘플의 uncertainty가 충분히 작다면 믿을만한 instance들이니 uncertainty를 줄여주는 뒤 term의 영향력은 줄고 앞 term에서 수행되는 instance discrimination에 더욱 집중할 수 있도록 설계된 것입니다.
이후에는 아래 수식 (11)에 해당하는 KL regularization loss \mathcal{L}_{\text{KL}}까지 함께 붙여 사용하게 됩니다. 이는 각 비디오의 분산을 줄일 때 아예 0으로 붕괴되어버리는 현상을 방지하고자 비디오의 분산이 항등행렬 분포를 따라가도록 규제해주는 것입니다. \mathcal{L}_{\text{KL}}은 비디오 분포에 직접적으로 영향을 미치기 때문에 실제로 해당 loss의 가중치에 따라 성능이 꽤나 크게 좌지우지되는 것을 후에 확인해볼 수 있습니다.
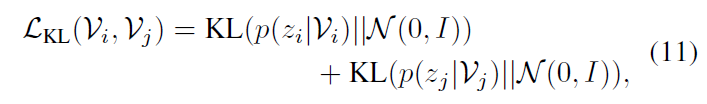
최종적으로 학습에 관여하는 loss \mathcal{L}_{\text{ProViCo}} = \mathcal{L}_{\text{stoc}} + \beta{} \cdot{} \mathcal{L}_{\text{KL}} 입니다.
이렇게 해서 ProViCo가 제안하는 확률적 embedding 공간 상에서의 represenation learning 방법론에 대해 모두 알아보았고, 이제 실험 부분으로 넘어가겠습니다.
3. Experiments
ProViCo 방식으로 backbone 모델들을 학습시키고, 이렇게 학습한 표현력을 Action recognition, Video retrieval task에 대해 평가합니다. Backbone 모델들은 R3D-18, R(2+1)D-18을 사용하였고 데이터셋으로는 Kinetics400(K400), UCF101, HMDB51이 사용되었습니다.
평가를 위해 대용량 데이터셋(K400, UCF101)으로 사전학습을 마친 backbone 뒤에 FC layer 하나를 붙인 후 평가할 데이터셋(UCF101, HMDB51)의 학습 split으로 재학습을 수행하는 일반적인 linear probe 방식을 동일하게 사용하였고, 재학습을 수행할 때 FC layer만 학습시키는지, 앞 단의 backbone 모델까지 모두 학습시키는지에 따라 finetuning 여부를 다르게 표시하게 됩니다. 자세히는 뒤 표와 함께 설명드리겠습니다.
3.1 Action Recognition
Action recognition은 trimmed video에 대한 비디오의 action classification task입니다. 영상의 image classification과 유사한 task입니다. ProViCo는 Action recognition inference를 수행할 때 수식 (4)에서 얻은 sample들의 분류 결과를 평균 내어 사용했다고 합니다.
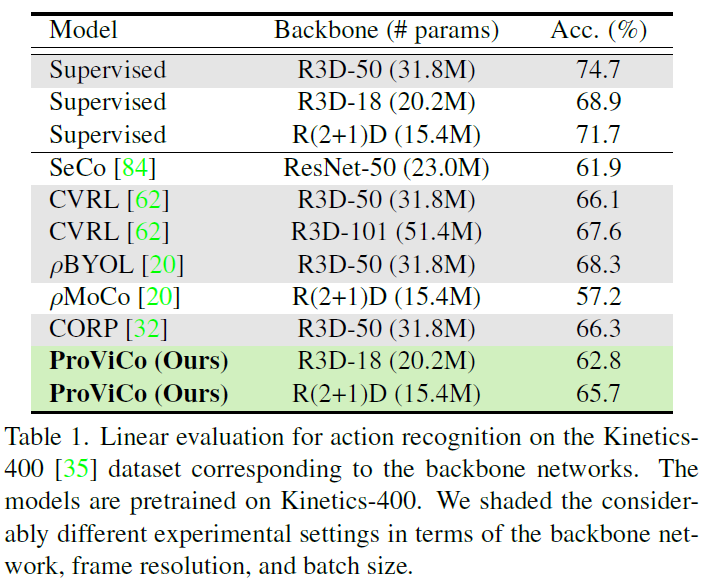
표 1은 K400 데이터셋으로 사전학습하고, K400 데이터셋으로 평가하는 경우 top-1 정확도를 보여주고 있습니다. 표 1의 가장 위 3행은 Fully-supervised 기반 학습 시 성능입니다. 기존 self-supervised 방법론들과 성능 측면에서 큰 차이가 있는데, 우선 ProViCo가 동일 backbone 기준으로 둘 간의 gap을 줄인 것을 볼 수 있습니다.
해당 task는 backbone 모델 뿐만 아니라 입력되는 clip의 해상도, contrastive learning을 수행하다보니 batch size에 따른 성능 차이가 큰데, 위와 같은 조건들이 현저히 다른 경우 회색 표시를 해두었다고 합니다. ProViCo는 기존 21년도 방법론들에 비해 모델 파라미터 수가 한참 떨어지는 backbone을 적용했음에도 불구하고 효율적으로 거의 유사한 성능을 내는 것을 볼 수 있습니다.
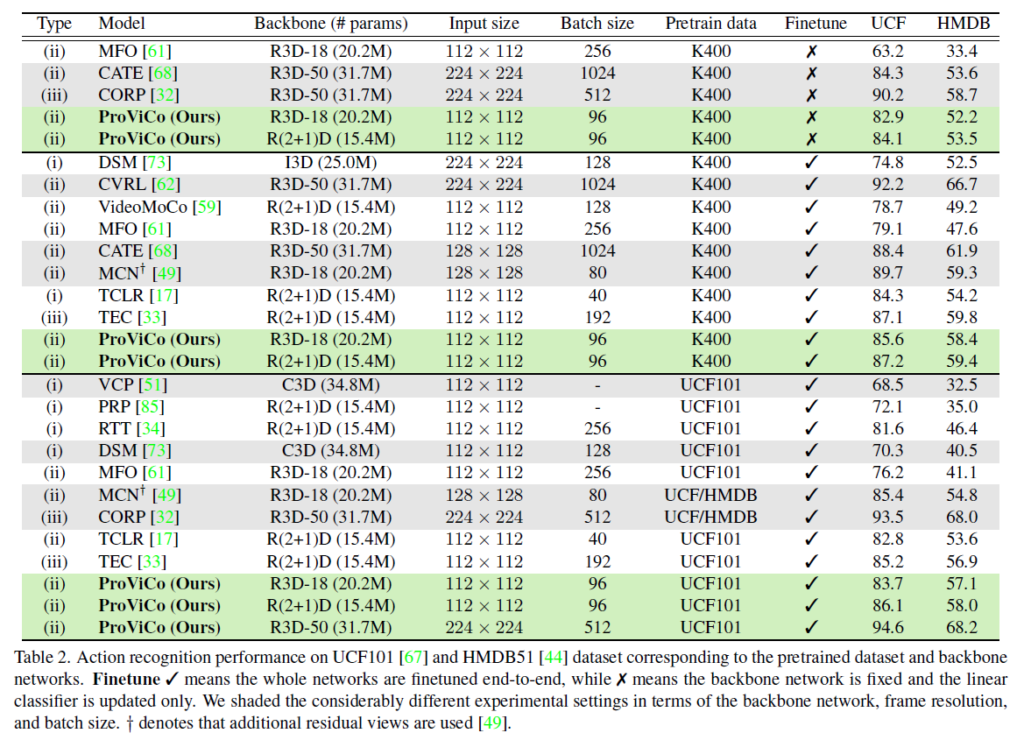
표 2도 마찬가지로 Action recognition task에 대한 벤치마킹 실험입니다. 표가 검정색 실선 기준 3덩어리로 나눠지는데, 가장 위는 K400으로 사전학습하되 평가 데이터셋에 대한 재학습 시 가장 뒤 FC layer만을 학습하는 경우의 성능입니다. 가운데는 동일한 K400으로 사전학습하지만 재학습 시 backbone 모델까지 학습되는 경우를 의미하고, 마지막으로 가장 아래 부분은 평가 데이터셋의 사전학습 split으로 사전학습을 진행하고, 재학습, 평가 split으로 각각 재학습하고 평가하는 경우입니다. 해당 split은 학계에서 다들 사용하는 protocol을 동일하게 적용했다고 합니다.
이전에 ProViCo의 UntrimmedKinetics400 데이터셋 사전학습을 진행해보려 한 적이 있었는데, ProViCo에서 비디오 당 2개의 clip만을 샘플링하는게 적은 것처럼 보일 수 있어도 이는 프레임 32(16*2)개이기 때문에 (1비디오 == 32영상)을 의미하게 됩니다. (물론 3D backbone을 태우기에 뒤쪽 학습 단까지 직결되는 것은 아닙니다.) 비디오에서 batch size 1이 결국 영상 단에서는 32만큼을 늘리는 것과 유사해지기 때문에 실제로 batch size나 clip resolution 조절에 따른 필요 메모리 차이가 굉장히 컸었습니다. 학계에서도 물론 메모리나 연산량적 측면에서의 효율성을 무시할 수 없고, contrastive 수행 과정에서 batch size에 따른 성능 차이가 꽤나 발생한다는 점을 다들 알고 계실 것입니다. 저자도 이러한 하이퍼파라미터의 차이와 효율성을 중점적으로 ProViCo의 우수성을 계속 이야기하고 있습니다.
표 2에서 (i)은 pretext task 기반 방법론, (ii)는 contrastive learning 기반 방법론, (iii)은 pretext task + contrastive learning 기반 방법론인데, 유사한 조건 하에 (ii)에 해당하는 ProViCo가 (iii)과 같이 복잡한 방법론들보다도 좋거나 견줄 만한 성능을 낸다는 점도 강조하고 있습니다.
3.2 Video Retrieval
기존 방법론들은 보통 추출한 video feature간 cos 유사도를 통해 retrieval 성능을 측정하는데, ProViCo는 수식 (9)의 매칭 확률을 기준으로 retrieval을 수행했다고 합니다. Cos 유사도를 기준으로 retrieval을 수행한 성능은 논문의 appendix에 있으니 궁금하신 분들은 찾아보시면 좋을 것 같습니다.
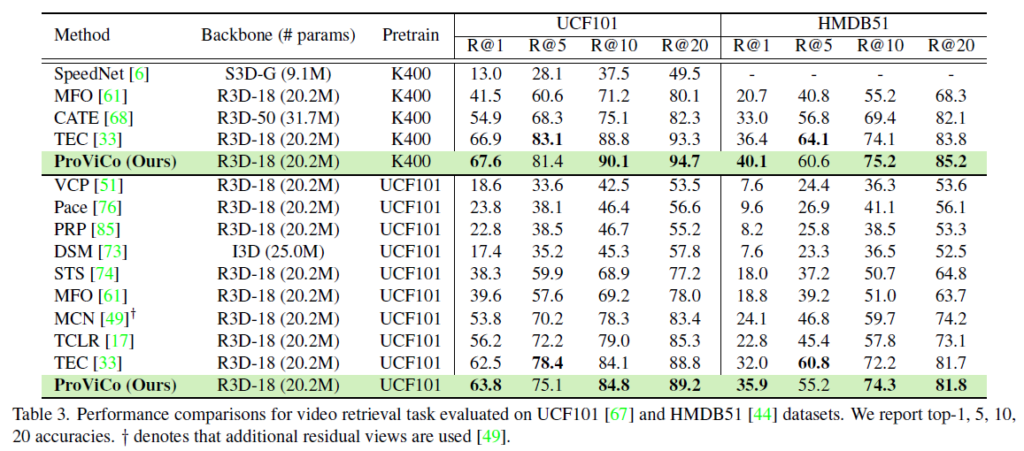
표 3에서는 사전학습 데이터셋(K400, UCF101)에 따른 평가 성능입니다. 기존의 21년도 방법론들보다 대부분의 Recall 기준에서 높은 값을 보여주고 있네요. 특히 top-1 성능이 기존보다 두드러지게 높아진 것을 볼 수 있습니다. 저자는 이에 대해 다른 비디오에서 나온 clip을 모두 negative로 두며 hard positive를 놓치고 있는 기존 방법론들과 다르게, ProViCo의 확률적 embedding 공간 상에서의 거리 기준 positive sampling 방식이 retrieval에서 확실히 잘 동작했다고 이야기하고 있습니다.
3.3 Ablation Study and Analysis

우선 표 4는 최종 loss에서의 \mathcal{L}_{\text{KL}}의 weight 값 \beta{}와 수식 (4)의 reparameterization 과정에서 분포로부터 몇 개의 샘플을 가져올 것인지에 대한 값 K의 ablation 결과입니다.
먼저 아래 K에 따른 성능을 먼저 보겠습니다. 일반적으로 전체 분포를 추정하기 위해 많은 수의 샘플을 가져와 거리를 계산할 수록 실제 분포에 가까워질 것입니다. 그렇기에 K가 커질수록 성능이 높아지는 것을 볼 수 있지만, Monte-Carlo estimation에 따라 총 K^{2}번의 연산이 계속해서 수행되기 때문에 저자는 연산량과의 trade off를 고려해 적절한 값인 10을 사용했다고 합니다.
다음으로 \mathcal{L}_{\text{KL}}은 비디오의 확률적 embedding 공간 상에서의 분포를 직접 조정하기 때문에 \beta{}에 따라 성능이 크게 변할 것임을 짐작해볼 수 있었습니다. 역시나 값에 따른 성능 차이가 유의미한 수준임을 알 수 있었고, \beta{}=10^{-5}인 경우 \mathcal{L}_{\text{KL}}의 역할인 분산이 0으로 붕괴되는 것을 막는 역할을 제대로 수행하지 못해 결국 \mathcal{L}_{\text{stoc}}이 발산하게 되었다고 합니다.
추가로 appendix에 저자가 \beta{}에 따른 분포를 시각화하기 위해 sub-dataset에서 feature를 3차원으로 줄이고 수행한 toy 실험이 있습니다.
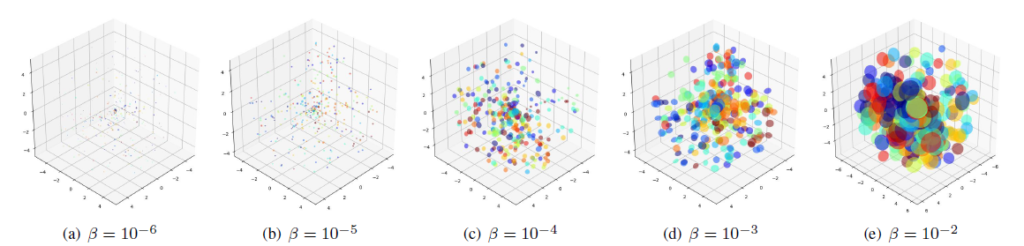
위 그림을 통해 \mathcal{L}_{\text{KL}}이 너무 크게 관여하는 경우 분포의 분산을 키우며 클래스끼리 분별력을 갖지 못하는 상황으로 만들어준다는 것을 알 수 있습니다. 반대로 너무 sparse해지는 경우 또한 앞선 경우처럼 분산이 0으로 붕괴되거나 모델의 표현력에 저해가 될 수 있기에 \beta{} 적절하게 조절해주어야 한다고 이야기하고 있습니다.
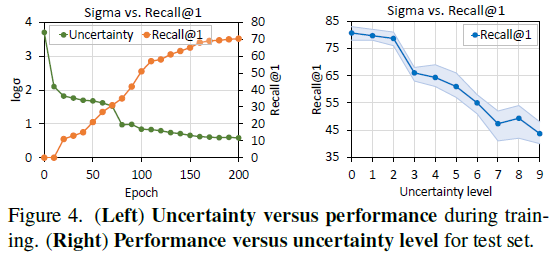
그림 4의 왼쪽은 학습 중 \mathcal{L}_{\text{stoc}}이 줄여주는 uncertainty 값에 따른 정확도 향상 그래프입니다. 오른쪽 표는 inference 시 uncertainty 값을 10개의 level로 나누고, 입력되는 instance의 uncertainty에 따른 추론 시 정확도 성능을 보여주고 있습니다. 두 상황 모두 uncertainty가 줄수록 실제 reliable한 instance이기에 좋은 방향으로 학습되거나 안정적인 예측을 수행한다는 점을 시사하고 있습니다. 저자가 uncertainty로 정의한 분산 값이 유효했음을 입증하고 있습니다.
3.4 Qualitative Results

마지막으로 확률적 embedding 공간에서의 거리를 기준으로 얻어낸 hard positive 샘플의 유무에 따른 retrieval에서의 정성적 결과입니다. ProViCo가 확실히 기존에는 잡아내지 못하던 hard positive까지 가깝게 만들어주며 오류를 줄여냈다는 것을 보여주고 있네요.
이상으로 리뷰 마치겠습니다.
감사합니다.
안녕하세요. 김현우 연구원님.
좋은 리뷰 감사합니다.
앞선 세미나에서도 그랬지만, 리뷰에서 정말 상세하고 꼼꼼히 논문을 다뤄주셔서 이해하기 크게 어려운 부분이 없는 것 같습니다.
제가 지금 작성하고 있는 코드에서도 KLD Loss를 사용해서 궁굼한 점이 있는데요. 비디오의 임베딩 분포 p(z|V)가 해당 분포에서 샘플링된 10개의 포인트로 들어가는 것으로 이해하였는데, kl div loss의 경우 입력이 합이 1이 되는 분포 형태가 아니면 발산하는 문제가 있는 것으로 알고 있는데, 혹시 저렇게 p(z|V)에서 항등 분포로 추출한 벡터는 이러한 조건을 자연히 충족하나요? 혹은 무언가 손실함수에 입력하기 전에 전처리를 해주나요.
감사합니다!
본 코드에서는 KL Divergence에 대한 수식을 따로 구현하여 loss에 넣어주기에 torch에서 사용하는 KL Divergence loss와 입력 및 사용법이 좀 다를 수 있을 것 같습니다. KL Div 입력값의 합이 1이 아니면 발산하는 문제는 처음 접하였는데, 이에 대해 좀 더 살펴보아야 할 듯 합니다.
결론적으로 코드 상에서의 입력값이 조건을 충족하거나 전처리하는 부분은 따로 보이지 않습니다.
안녕하세요 김현우 연구원님, 좋은 리뷰 감사합니다.
우선 기존 ssvrl에 사용되던 deterministic embedding은 전체 비디오에서 하나의 특징을 추출하고 이를 동일한 feature space에 위치시킨 뒤 task를 수행하는 것이라고 이해하였습니다.
수식(4)에 관해 궁금한 점이 있는데요, 수식(4)의 \sigma(V)와 \mu(V)는 위의 appendix의 수식에서 정의된 함수와 동일한 함수인가요? 아니면 각 clip별 정규 분포에 대한 평균과 표준 편차를 의미하는 것인지 궁금합니다.
감사합니다.
수식 (4)에 나타난 \sigma(V)와 \mu(V)는 각각 appendix에서의 수식 (2), (3)과 같은 값을 의미합니다. Clip은 비디오보다 작은 단위이기에, clip 분포의 평균과 분산인 \mu(c), \sigma(c)들을 GMM으로 aggregate 하였을 때 그 GMM의 평균과 분산이 \sigma(V)와 \mu(V)에 해당한다고 이해하시면 됩니다.
Appendix에 담긴 수식이다보니 notation이 좀 다르게 표현되었다는 점을 참고하시면 좋을 것 같습니다.
좋은 리뷰 감사합니다.
저도 예전에 읽은 논문 이지만 요즘 논문 방향을 같이 고민하는 입장에서 떠오르는 새로운 의문(?) 및 방향이 떠올라서 댓글 남깁니다.
해당 방법론이 GMM을 구성할 때 모든 분포간의 영향력을 동일하게 가져가는 것 같습니다. 원래 GMM은 분포간의 혼합계수도 추정하는 것이 기본인데 말이죠. 아마도 Trimmed 비디오를 사용하기 때문에 Background를 고려하지 않은 모델링인 것 같습니다.
하지만 이를 Untrimmed 비디오로 가져오면 혼합계수를 반드시 추정해야할 것 같은데 이 부분에서 attention 방식으로 처리하는 것이 어떤지 의견이 궁금하네요.
가령 WSTAL 분야에서 actionness score를 혼합계수로 사용한다든지 등등 해당 의문에 대해서 의견을 듣고 싶습니다.